Enhanced Quantum Inspired Grey Wolf Optimizer for Feature Selection

Published Online June 2020 in MECS DOI: 10.5815/ijisa.2020.03.02

Feature selection is a preprocessing data operation which used to remove redundant and unimportant features from datasets. Using refined datasets for machine learning allows for better learning performance and accuracy during training and test times.

Feature selection methods can be classified into three methods, including filter methods, embedded methods and wrapper methods [1]. With filter methods most features that can describe data are selected according to specific criteria. It doesn’t depend on the learning algorithm or post data processing technique [2]. While embedded methods use the machine learning algorithm itself to make feature selection [3, 4] like using support vector machine [5] and perceptron net [6]. Wrapper methods use machine learning algorithms to evaluate features selected using a feature selection operation. Although it may take longer time than other methods but it connects the learning task with the selected features producing better learning accuracy. Wrapper methods use heuristic algorithms [7, 8, 25] and bio-inspired algorithms [9, 10, 11, 12] with all these solutions we couldn’t find a general solution for feature selection due to the wide range of applications that need feature selection as a suboperation.

Bio-inspired algorithms are based on nature evolution and behaviors of some creatures from different categories animals, insects, birds and even sea creatures. These creatures deal with many problems  that can be categorized as search or optimization problems like looking for food and hunting. Most of them depend on swarm activities to achieve a specific task. From computer science perspective we have multiple complex optimization problems-like feature selection-that needs to be solved. Most of these problems can find solutions using bio-inspired algorithms [14]. In this paper our focus is on Grey Wolf Optimizer (GWO) [15] which is a relatively new optimization algorithm that mimics grey wolves leadership and hunting technique in nature. Two versions of GWO were proposed, probabilistic and binary. In probabilistic GWO each wolf takes a position value between 0 and 1 where with binary GWO wolves’ positions take a binary value of 0 or 1. Recently, unit commitment problem was solved using quantum inspired binary grey wolf optimizer [16]. In this paper we introduce another enhanced integration between quantum-inspired operations and binary-GWO to solve feature selection problem.

Quantum computing and bio-inspired algorithms proved the ability to solve hard problems with simple operations and techniques. Most quantum algorithms use the power of, quantum parallel processing ability and probabilistic representation of quantum data like Grover search algorithm [17] which enhanced the search time in structured database containing N items to be O (^N) [17]. Shor factorization algorithm [18] is another quantum algorithm that solves factorization problem faster using quantum operations. Some quantum operations are not restricted to quantum computers; it can be simulated or applied on classical hardware too like qubit representation and rotation operation [19].This leads to quantum-inspired algorithms that use quantum ideas with classical algorithms to get better performance for solving problems. A wide variety of quantum inspired algorithms exist in all computing fields [20, 21, 22, 23]. Merging Bio-inspired algorithms with quantum operations give the advantage of techniques, randomness and heuristic advantage from one side and parallelism from the quantum side.

The effect of quantum operations with bio-inspired algorithm on feature selection is not clear yet. Many quantum inspired algorithms were developed to solve multiple computing and engineering problems [20, 21, 22, 23, 24, 26, 27] but rare of them was used with feature selection [28, 29]

In this paper we introduce an enhanced binary grey wolf optimizer using quantum operations producing a quantum-inspired binary GWO to provide a powerful feature selection method with high accuracy and good performance.

To evaluate our proposed method we used K-nearest neighbor algorithm [30] on multiple datasets to compute the learning error and number of features excluded during training. The best solution is computed as the lowest number of features used to get the lowest learning error. Although using Binary-GWO for feature selection is applied in [38] and gives good results our enhanced quantum inspired GWO algorithm gives better running time when applied on the same datasets. The rest of the paper is organized as follows; section 2 gives a background about quantum computing and GWO. In section 3 we discuss our proposed algorithm in detail. Testing results and analysis is introduced in section 4, and finally we conclude our work in section 5.

• II.    Background

• A.    Quantum computing

A Quantum bit (Qubit) is the storage unit in quantum system which can hold |0) state, |1)state or both states with specific probabilities. Mathematically; a qubit |y) can be expressed as a linear combination of states |0) and 11) [19].

| ^ = a\ 0) + 6 | 1 (1)

Where a and b are complex coefficients satisfying the condition |a|2 + |b|2 =1 and

|a| 2 = probability of finding |y> in state |0),

|b| 2 = probability of finding |y> in state |1).

Operators or gates are used to implement mathematical and logical operations on qubits that are represented as vectors. A matrix representation for an operator is a simple way to understand how a quantum system can be transformed from one state to another. The Pauli operators are basic quantum operators denoted as I, X, Y, and Z, where I is the identity operator, and X is called sometimes NOT operator. Table 1 summarizes Pauli operators with their corresponding matrices [19]. Other quantum gates are much more complicated such as Feynmann gate, Toffoli gate, Swap gate, Fredkin and Peres gates [31]. Rotation gates are another type of quantum gates which represent rotating a quantum bit around the Z-axis producing Rz-gate and rotating a quantum bit around the Y-axis producing Ry-gate and rotating a quantum bit around the X-axis producing Rx-gate the matrices for rotation gates are [31];

Rx ( e ) =

cos( e )

- i sin( e )

- i sin( e ) cos( e )

( cos( e )   - sin( e ) A

L sin( e )   cos( e ) J

Г - i ^e Rz ( e ) = I

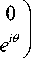
Quantum Rotation matrices are one of the ideas used with classical algorithms to generate quantum inspired algorithms [26, 27]. Here we used rotation gate in equation (3) to control the update steps of GWO to propose our quantum-inspired algorithm to explore the effect of quantum operations and bio-inspired algorithms on feature selection.

Table 1. Quantum gates and their matrices

Gate Name	Matrix
I	Г 1  о A L о   1 J
X	Г о   1 A L 1  о J
Y	Г 0   - i A L i   0 J
Z	Г 1   о a L о - 1 J

• B.    Bio-Inspired algorithms

In recent years many bio-inspired algorithms were proposed and tested on many problems in different fields of technology. Honey bee swarms behavior inspired Derviş Karaboğa to propose the Artificial Bee Colony (ABC) Algorithm to solve numerical optimization.

Whale Optimization Algorithm (WOA) [32] and Grey Wolf Optimizer (GWO) proposed by Seyedali Mirjalili [15] that are based on the idea of encircling the prey. Elephant Search Algorithm (ESA) also mimics the search technique of elephants. Elephants are grouped to males and females, each group search in specific parts. Artificial Algae Algorithm (AAA) [33] is based on evolutionary process of micro algae. Fish Swarm Algorithm (FSA) [34] is based on fish colonies technique for food searching process. All these examples and more [24] form the new brand of nature-inspired algorithms. GWO [15] is a motivated mathematical modeling of natural grey wolves’ technique of hunting. Grey wolves live in groups categorized as, alpha, beta, delta and omega wolves where alpha wolves are the group leaders and responsible for decision making process during hunting operation, beta wolves help alpha wolves in their tasks, delta wolves are set in the back helping beta and alpha wolves which are the last wolves allowed to eat. Finally, any other wolf in the group is called omega wolves which don’t contribute in the hunting process. The hunting operation start with chasing the prey and trying to make a circle around it and make this circle narrower with each move a grey wolf make until the alpha wolves take the decision of attacking the prey. To model this operation in mathematical form, each wolf α, β, and δ is given two random vectors for its where r 1α , r 1β , r 1δ are first random vectors in [0,1] interval for α, β, and δ wolves and r 2α , r 2β , r 2δ are second random vectors in [0,1] interval for α, β, and δ wolves. Each wolf has two coefficient vectors calculated as the following equations [15],

Aa = 2 ar1a - a(5)

Ap = 2 arp- a(6)

As = 2 ar -- a(7)

C = 2 Г2а(8)

Ce = 2 r2 p

Cs = 2 K25(10)

Where components of a are linearly decreased from 2 to 0 during iterations using equation (11) [15]

• -2/

a = 2--—(11)

max t

Distance vectors between the prey and each wolf is calculated as follows:

Da = C .Xa - X/(12)

Dp = Cp.Xв - X/(13)

Where X a , X p , X s are position vectors for а, в, and 5 wolves respectively and X i is the position for best solution wolf in the i^th iteration. Position updates for α, β, and δ wolves each iteration is applied according to equations (15, 16 and 17) [15]

Xa (t + 1) = Xa (t) - Aa ’ Da(15)

Xp (t +1) = Xp (t) - Ap • Dp(16)

Xs (t +1) = Xs (t) - As • Ds(17)

Where t is the iteration number, and then X is updated according to equation (18) [15]

X ( t + 1 ) = ( X a ( t + 1 ) + X p ( t + 1 ) + X s ( t + 1 ) ) /3 (18)

The pseudo code for GWO is [15],

Initialize the grey wolf population

Initialize α, A and C

Calculate the cost values of grey wolves

Save the best grey wolf as alpha wolf

Save the second best grey wolf as beta wolf

Save the third best grey wolf as delta wolf while (iteration < maximum iteration)

Decrease a for each grey wolf

Generate the coefficient vectors for alpha, beta, delta

Calculate the distance vectors

Calculate the trial vectors

Update the position of each grey wolf end for update α, A and C

Calculate the cost values of updated grey wolves

Update X _a, X p , X ₈.

increase iteration one end while return alpha wolf.

• III.    Literarture Review

Feature selection is one of the most significant operations in machine learning while GWO is a strong, simple and low cost optimization methodology. Working on enhancing GWO to produce better results is still a fresh research point. A binary version of GWO was used for feature selection in [11]. The authors introduced two methods to binarize wolves positions generated from

GWO updates. The first method generate a binary value for each wolf using individual steps and then a use of stochastic crossover is implemented to find the new position of the binary grey wolf. The second method use sigmoid function with a random threshold to convert continuous values of wolves’ positions to binary values. Both strategies were compared to Genetic Algorithm (GA) and Particle Swarm Optimization. A newer version of binary GWO that use a competitive strategy between wolves was introduced in [9] to solve feature selection for Electromyography signals to classify hand movements. In this algorithm each two wolves compete with each other and the winner moves to the new population while the looser update its position by learning from the winner. Working on large datasets with GWO is achieved in [10] using an integration of two mutation phases to enhance the exploitation and exploration properties of the proposed algorithm in order to applying the sigmoid function to binarize continuous wolves positions values generated after each iteration. The authors used K-NN classifier with test datasets which make time consumption with large datasets. Combining GWO with Antlion optimizer (ALO) is another solution for feature selection with large dimensional datasets that contain small instances [13] the hybrid solution called ALO-GWO gives better performance than working with a GWO or ALO alone and other optimizers like PSO and GA. Another combination between Binary Bat Algorithm (BBA) and PSO called HBBEPSO for Feature selection is implemented in [35]. We noticed that hybrid algorithms prove its efficiency over single optimizers for feature selection. Referring to Quantum inspired heuristic algorithms used for feature selection we found that rare implementations are available. A recently introduced quantum inspired Evolutionary Algorithm (EA) by A. C. Ramos and M. Vellasco, in [36] that works on Electroencephalography (EEG) signals to reduce redundant features for Brain-Computer Interface systems. Using quantum operations with EA produce a better exploration and exploitation which produce a faster and better solution as a brain signal it needs time frequency characterization analysis which is achieved using Wavelet Packet Decomposition while the classification task is implemented using Multilayer Perceptron Neural Network. Reviewing the literature we didn’t find any implementation of combining quantum operations with GWO for solving feature selection and this was the motivation leading to our research work in this paper.

• IV.    Enhanced Quantum-Inspired Binary Grey Wolf Optimizer

In the original version of GWO all wolves take continuous values in [0,1] for its positions while in Binary-GWO (BGWO) a wolf’s position takes binary values and calculating this binary value is maintained using sigmoid function implementation on Grey wolves positions’ values [38]. A quantum-inspired BGWO was introduced in [16] to solve unit commitment problem. Here we propose an Enhanced Quantum-Inspired BGWO

(EQI-BGWO) to solve feature selection problem. In EQI-BGWO, wolves’ positions take binary values and these positions are updated according to specific qubit vector and a quantum rotation gate, where each wolf has its own qubit and rotation gate. We used the Ry (θ) gate equation (3). The original GWO depends on A and C equations to update the position of each wolf, while in EQI-BGWO; updating the wolves positions’ depends on both the qubit associated to each wolf and each wolf’s θ angle, where updating 0 during the course of iterations depend on two probabilistic random values γ and ζ as shown in the following equations,

O (t +1) = za Ya E (X“ (t) -X(t)) * 2n(19)

ep (t +1) = Ze Ye E (Xв (t) -X(t)) • 2n(20)

ds (t +1) = Zs Ys E (Xs (t) -X(t)) • 2n(21)

z = ^1.n(22)

Zв = M(23)

Z5 = Х3Л(24)

and λ 1 , λ 2, λ 3 are random values for alpha, beta and delta wolves respectively and (^ is called theta magnitude for alpha wolf. Each wolf’s qubit vector called Q is rotated using its corresponding rotation angle as expressed in equations (25), (26) and (27).

Qa (t + 1) = Ra (Oa (t + 1))* Qa (t)

Qe (t +1) = Re 0 (t +1))Q (t)

Qs (t +1) = Rs (0s (t +1)).Qs (t)

Where Q take the form of a single qubit such that,

| Qa >= aa |0>+ ba |1>

| Qe >= ap |0>+bp |1>

| Qs >= as |0>+ bs |1>

The initial value of a _a , b _a , a _e , b _e , a _s and b _s will be

• 1/  2 , where wolves’ positions are updated according to

the qubit vector probability of state |1) such that,

Xa (t + 1) = Xa (t) • b^(t + 1)(31)

Xв (t +1) = Xв (t) • b^(t +1)(32)

X ₅ (t + 1) = X ₅ (t ) • b 2 ( t + 1)             (33)

and feature reduction; we set e = 0.01 in our work

To convert the probabilistic values of wolves’ positions into binary values a simple thresholding operation is used as follows,

X . ( , + 1 ) =! ‘ f ^X a ⁽ ' ^{+ 1 ) 6} b .2 ( t ⁺ 1) [ 0 otherwise

The same thresholding is done for beta and delta wolves according to each wolf qubit probabilities of state |1). The final step is computing the new best solution which is a combination of the three wolves α, β, and δ according to equation (18). To get a binary value forX, a procedure of two steps is applied

• 1-    Apply a sigmoid function equation (35). onX to get F(X) _

• 2-    Compare F( X) to a random value X such that

• a.    X = 1 if F(X) >  s

• b.    X = 0 if F(X)< s

where s takes a value between 0 and 1 where the sigmoid function takes the form:

sigm ( p ) =    ^{1                     (35)}

1 + e^{( p} )

where p represent the position value and take values in range [0, 1].

V. Feature Selection using EQI-BGWO Experimental Results

Feature selection is an important process in machine learning [7, 8, 14]. It is used to reduce the number of features in a dataset in order to simplify the learning process while keeping the optimal learning accuracy. With big datasets and complex learning tasks feature selection is important. To evaluate the used EQI-BGWO with feature selection we used K-NN classifier which is a supervised machine learning algorithm that uses labeled dataset to produce a learning model. In our experiments we used four datasets from UCI machine learning repository [37] described in table 2. The evaluation criterion is to have the least number of features with minimum error rate. The fitness function is a minimization problem that has the form shown in equation (36) [3 8] as follows,

Fitness = cE_R

R

(D)

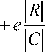
Where cE R (D) is the error rate for the classifier of condition attribute set, R is the length of selected feature subset, and C is the total number of features, c ϵ [0,1] and e = 1-c are constants to control the classification accuracy

Table 2. Datasets structure

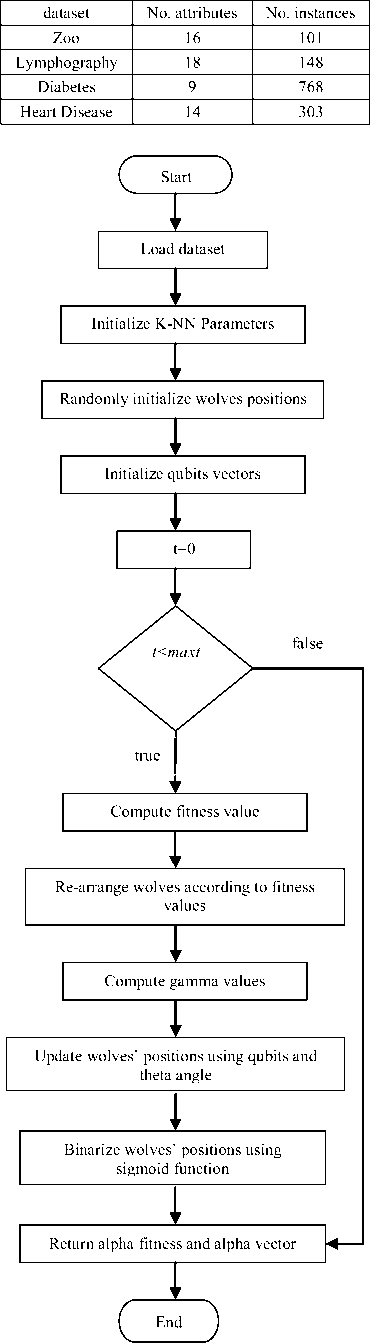
Fig.1. Experiments Steps

A flowchart of our experiment steps using EQI-BGWO is presented in figure (1). Our experiments are applied on MATLAB 2015 platform using Intel coreI7 processor and 12 GB of RAM. Initialization of experiments used 5 agents and 70 running iterations for both BGWO and EQI-BGWO. To get accurate average values, we implemented 10 runs on each dataset using BGWO and EQI-BGWO methods. Results after each run are summarized in Tables 3, 4, 5, 6, 7, 8, 9 and 10. The trial column represent a running time number, the fitness column represent the fitness value equation (36) [38] of running BGWO and EQI-BGWO on each dataset, number of eliminated features column represent the features eliminated from the original data set using the feature selection algorithm applied and Global optima iteration column is the iteration number at which the global optima of the fitness value is reached. Each record in the table represents a running time output.

Table 3. Results of applying BGWO on Zoo dataset

Trial	BGWO Fitness value	No. Eliminated Features	Global optima iteration
1	0.0438	8	53
2	0.1039	5	7
3	0.0632	8	19
4	0.1409	8	8
5	0.0457	5	10
6	0.1428	5	6
7	0.1027	7	29
8	0.1046	7	3
9	0.0845	5	3
10	0.0826	8	5
Average	0.09147	6.6	14.3

Table 4. Results of applying EQI-BGWO on zoo dataset

Trial	EQI-BGWO Fitness value	No. Eliminated Features	Global optima iteration
1	0.1027	7	15
2	0.0444	7	31
3	0.1221	7	38
4	0.0451	6	12
5	0.0444	7	32
6	0.1021	8	11
7	0.1033	6	64
8	0.0257	6	11
9	0.0451	6	40
10	0.0444	7	43
Average	0.06793	6.7	29.7

Table 5. Results of applying BGWO on Lymphography Dataset

Trial	BGWO Fitness value	No. Eliminated Features	Global optima iteration
1	0.5669	9	8
2	0.5028	4	50
3	0.4604	8	9
4	0.4883	7	18
5	0.5948	7	29
6	0.4732	9	5
7	0.5412	7	40
8	0.5697	4	21
9	0.5792	11	5
10	0.6081	7	5
Average	0.53846	7.3	19

Table 6. Results of applying EQI-BGWO on Lymphography dataset

Trial	EQI-BGWO Fitness value	No. Eliminated Features	Global optima iteration
1	0.4621	5	29
2	0.5295	4	39
3	0.5546	7	4
4	0.5401	9	47
5	0.5663	10	10
6	0.5546	7	39
7	0.5774	4	17
8	0.4872	8	55
9	0.4921	6	40
10	0.4921	11	15
Average	0.5256	7.1	29.5

Table 7. Results of applying BGWO on Diabetes dataset

Trial	BGWO Fitness value	No. Eliminated Features	Global optima iteration
1	0.2575	0	5
2	0.2357	3	5
3	0.2641	3	35
4	0.2537	3	15
5	0.2680	4	20
6	0.2383	3	5
7	0.2744	3	55
8	0.2783	4	3
9	0.2756	2	8
10	0.2551	4	9
Average	0.26007	2.9	16

Table 8. Results of applying EQI-BGWO on Diabetes dataset

Trial	EQI-BGWO Fitness value	No. Eliminated Features	Global optima iteration
1	0.2305	3	8
2	0.2331	3	19
3	0.2254	3	15
4	0.2551	4	35
5	0.2499	4	15
6	0.2421	2	8
7	0.2357	3	20
8	0.2048	3	5
9	0.2615	3	15
10	0.2551	4	10
Average	0.23932	3.2	15

Table 9. Results of applying BGWO on Heart Disease dataset

Trial	BGWO Fitness value	No. Eliminated Features	Global optima iteration
1	0.1039	5	10
2	0.0839	6	22
3	0.1835	2	7
4	0.0457	5	5
5	0.1403	9	25
6	0.1409	8	5
7	0.1622	5	3
8	0.0457	9	5
9	0.1046	4	41
10	0.1634	3	15
Average	0.11741	5.6	13.8

Table 10. Results of applying EQI-BGWO on Heart Disease dataset

Trial	EQI-BGWO Fitness value	No. Eliminated Features	Global optima iteration
1	0.1682	6	34
2	0.1422	6	32
3	0.1667	8	15
4	0.1674	7	25
5	0.1878	7	65
6	0.1682	6	35
7	0.1789	8	45
8	0.1625	5	61
9	0.1299	5	51
10	0.1464	7	62
Average	0.16182	6.5	42.5

Comparing Average fitness values for each dataset using BGWO and EQI-BGWO is shown in figures 2, 3, 4, and 5. The comparison shows that average fitness value for zoo, Lymphography and Diabetes datasets is smaller for EQI-BGWO than BGWO while for Heart Disease Dataset the average value was 0.11741 for BGWO and 0.16182 for EQI-BGWO. This shows that EQI-BGWO gives better accuracy in most test cases.

Another comparison is for the average number of features that BGWO and EQI-BGWO eliminate from datasets shown in figures 6, 7, 8, and 9. The evaluation criterion for comparison is the larger number of eliminated features. Results show that for Zoo dataset BGWO eliminates 6.6 while EQI-BGWO 6.7 features and for Lymphography dataset BGWO eliminates 7.3 while EQI-BGWO 7.1 features and for Diabetes dataset, BGWO eliminates 2.9 while EQI-BGWO 3.2 features and finally for Heart Disease, BGWO eliminates 5.6 while EQI-BGWO 6.5 features. Gathering the lowest error value and larger number of eliminated features as an evaluation method, we conclude that EQI-BGWO is better than BGWO.

The global optima represent the best solution for an optimization problem. With K-NN algorithm, the global optima value is the best classification with least error rate [30]. In our working case when the error rate reaches a stable value, this is considered the optimal solution. Figures 10, 11, 12, and 13 show a comparison between BGWO and EQI-BGWO regarding iteration number of reaching global optima. Results show that BGWO reaches the global optima faster with Zoo, Lymphography and Heart Disease datasets while EQI-BGWO is faster with diabetes dataset. Generally, while reaching global optima is faster with BGWO, but the error rate is better with EQI-BGWO which is very important with machine learning tasks.

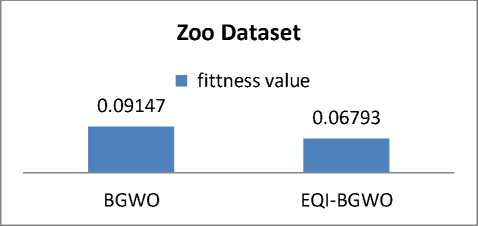
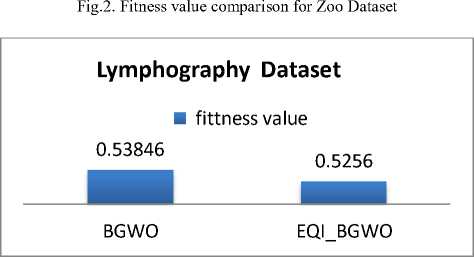
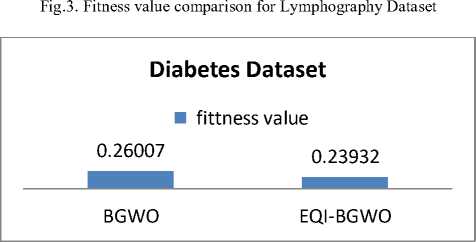
Fig.4. Fitness value comparison for Diabetes Dataset

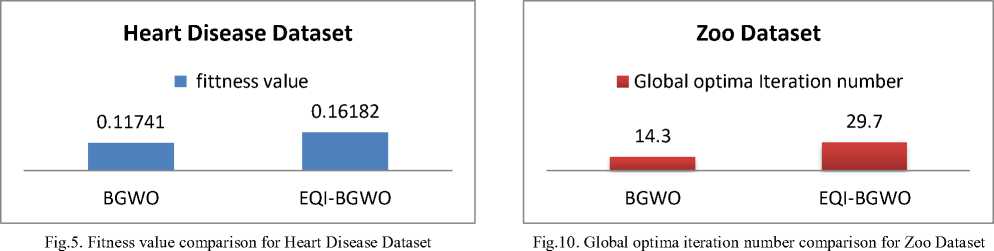
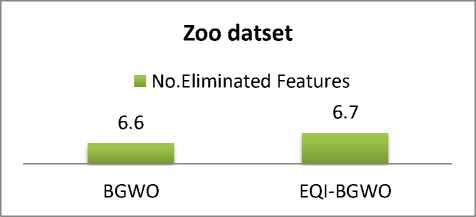
Fig.6. Number of Eliminated Features Comparison for Zoo Dataset

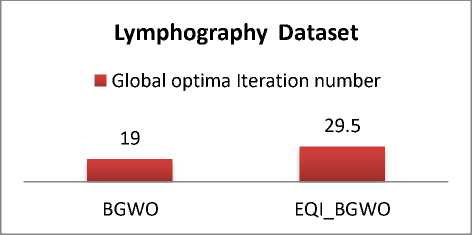
Fig.11. Global optima iteration number comparison for Lymphography Dataset

Lymphography Dataset

• ■ No.Eliminated Features

7.3 7.1

BGWO           EQI_BGWO

Fig.7. Number of Eliminated Features comparison for Lymphography Dataset

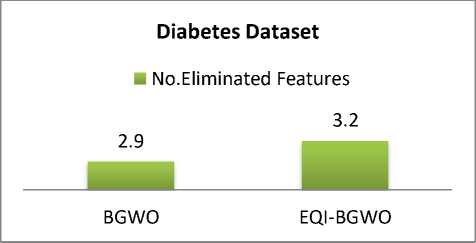
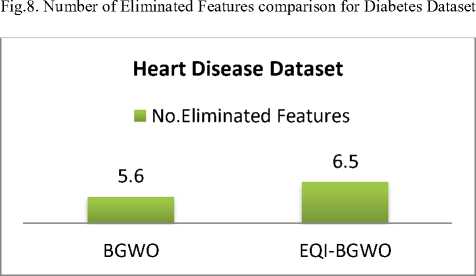
Fig.9. Number of Eliminated Features comparison for Heart Disease Dataset

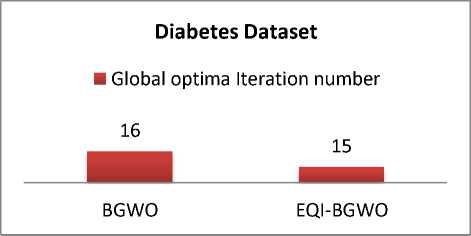
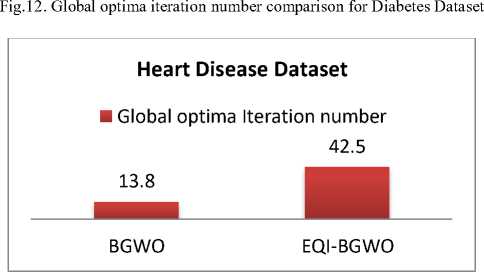
Fig.13. Global optima iteration number comparison for Heart Disease Dataset

Our experiments applied two versions of grey wolf optimizer: Binary GWO presented in [38] and our proposed algorithm called Enhanced Quantum Inspired-GWO which use quantum rotation gate associated to each wolf in order to control the update step of wolf’s position. K-nearest neighbor learning machine is used to evaluate the selected features after each iteration update of BGWO and EQI-BGWO. For zoo, Lymphography and diabetes datasets, lower error was gained using EQI-BGWO than using BGWO while with Heart Disease datasets BGWO give lower error but EQI-BGWO eliminates more features with all used data sets. These results ensures that there is no one best solution for feature selection as many factors can affect the whole output of a system like used data sets or the used learning machine but using quantum operations introduce a new point that can give better solutions.

• VI. Conclusion and Future Work

Feature selection is a very important problem in machine learning which has high impact on the learning operation. Multiple solutions for feature selection are proposed using bio-inspired algorithms and gave good results. GWO is an algorithm that has low computational cost. It was used to solve multiple optimization problems like feature selection. This motivates us to work on BGWO and proposes an enhanced version using quantum operations. In this paper we introduced an enhanced quantum inspired binary grey wolf optimizer to solve feature selection problem. Our work used quantum rotation gate to control the update criteria of the optimization algorithm steps. Results show that the update procedure of grey wolves’ positions using this quantum rotation gate produce speedups in weights update which lead to a better transformation between search spaces producing better solutions in most cases. This effective change produces better selection of features and consequently gave higher accuracy in the classification step. The application of EQI-BGWO here used small data sets to get an initial performance, but evaluating our approach with a wide Varity of datasets including large ones and different learning algorithms is targeted in our future work. Also trying other optimization problems would be another research point to consider.