Enhancement of Indoor Localization in WSN using PSO tuned EKF

Published Online February 2017 in MECS

Wireless Sensor Networks (WSN) [1] is a collection of sensor devices, which performs operations such as sensing and computing in various applications. This network is used in wide range applications such as Industry [2], Agriculture [3], Civil infrastructure [4] and Security [5]. Recent developments in WSN are popularly used for indoor applications [6]. The deployment of sensor nodes in random positions, impact on finding accurate locations of nodes. Generally, GPS system is used in WSN for determining location of nodes. But, due to various reasons practical implementations involves lot of difficulties [7]. Finding location of nodes is essential for indoor applications.

The techniques such as Received Signal Strength (RSS) [8], Time of Arrival (TOA) [9], Time Difference of

Arrival (TDOA) [10] and Angle of Arrival (AOA) [11] are used currently for finding location. These solutions are ineffective due to noise and multipath effects in wireless communications. The localization algorithms can be classified in to two types’ viz., centralized localization algorithm and distributed localization algorithm. In centralized localization algorithm the central node collects location information from all other nodes in network and perform localization task. The other techniques, all nodes in network execute algorithms and computes location information [12]. In this paper, the enhanced localization algorithm using Particle Swarm Optimization assisted Extended Kalman Filter (PSO-AKF) is proposed. After finding the locations, the communicate nodes are used locations and establish a route between source and destination node. The improvements are termed as Enhanced Localized Routing using PSO Assisted AKF.

Henceforth the paper is organized as follows section 2 explains the existing solutions from the literature. Particle Swarm Optimization (PSO), Kalman Filter (KF) are described in section 3. Section 4 illustrates the proposed mechanism in detail. The performance investigation and simulation outcomes are explained in section 5. Finally, section 6 concludes the paper.

• II.    Existing Solutions

The localization mechanism is important criteria in WSN for emerging applications. The existing solutions are finding locations based on GPS. But this method involves more complex and also consumes energy of a sensor node, which impact on poor network performance in terms of accuracy, Packet Delivery Ratio (PDR) and lifetime of network. In this section some of the existing solutions are explained.

The localization is important criteria in WSN for emerging applications. The existing solutions are finding locations based on GPS [13]. But this method is inaccurate and also consumes more energy of a sensor node, which leads network poor performance in terms of PDR, throughput and lifetime of network. In this section some of the existing solutions are explained.

GPS system can be used for localization of WSN in outdoor environment. It does not work well in the presence of obstacles and indoor environment [14]. Global Position system (GPS) gives inaccurate results and consumes more power [15]. Distributed Least Mean Square (DLMS) algorithm is used in the applications of localization and routing. DLMS algorithm is very simple in comparison with Distributed Recursive Least-Squares (DRLS) algorithm [16]. LMS algorithm has low SNR and less stable compare to DRLS algorithm and it offers good performance for very narrowband signals. DLMS algorithm requires external commands for control [17]. DRLS algorithm finds the location of nodes [18]. DRLS algorithm has faster convergence speed but this system is more complex [19].PSO is based on swarm intelligence. In PSO algorithm considers movement of group of birds, bees, school of fishes [20].The Kalman filter (KF) estimates unknown variables with precise values based on measurements over a time [21]. It has numerous applications in the field of signal processing,marine navigation, control of vehicles, aerospace. Extended Kalman Filter (EKF) is used to optimize the solutions of KF in nonlinear conditions.Extended Kalman Filter is optimized form of KF used in nonlinear environment [22].

The existing solutions in literature, finding the locations of node is inaccurate. In WSN, the location of node is important for finding the better routing path for communication. From the above information, in this paper Enhanced Localization algorithm is proposed and explained in section 4.

• III.    Related Work

The proposed method in this paper uses optimum mechanism i.e. Particle Swarm Optimization (PSO) which described in this section.

• A.    Particle Swarm Optimization

PSO is based on swarm intelligence. In PSO algorithm considers movement of group of birds, bees, school of fishes . Position of particle is denoted by Xi and velocity Vi then calculation of Vik+1 using the following Eq.1 and 2.

V ik+1 = w v ik + c 1 r 1 (p best - x ik ) + c 2 r 2 (g best - x ik )   (1)

X ik+1   =   X ik + V ik               (2)

Vik= velocity of node i at iteration k Xik=current position of node i at iteration k cl, c2 = acceleration constants rl, r2 = randomly generated numbers consistently disseminated in the range [0, 1]

w = inertia weight to control the scope of the search.

• B.    Kalman Filter

The Kalman filter (KF) estimates unknown variables with precise values based on measurements over a time . It has numerous applications in the field of signal processing,marine navigation, control of vehicles, aerospace. Extended Kalman Filter (EKF) is used to optimize the solutions of KF in nonlinear conditions.

• C.    Extended Kalman Filter

Extended Kalman Filter is optimized form of KF used in nonlinear environment which is given in Eq. 3 and 4.

х_к+ i = f(x_kk) + w_k            (3)

Zk = h.(x_kk) + v_k               (4)

Where xk = state vector wk = Process noise vector

Z _K = measurement vector

V_K = measurement noise vector

• IV.    Proposed Enhanced Localization

In this, the proposed Enhanced Localized Routing calculates nodes position using PSO Assisted AKF. Performance of the proposed method calculates the network performance by comparing with existing solution. Section 4.1 explains the proposed solution.

• A.   Determination of location of nodes using PSO-

• Assisted AKF algorithm

Consider a WSN in indoor environment where nodes are deployed randomly. In that some nodes do not know their position is known as agent nodes. Nodes which know their position is known as anchor nodes. Anchor nodes with known position (x1, y1, x2, y2,..............)T find distance of unknown agent nodes using Received Signal Strength( RSS). Distance between anchor node and agent node is given by Eq.5

P i = d i + e                        (5)

Where d , = ^(x - X ; )² + (y - yj²

e = location error due to noise (xi,yi) = position of ith agent node

(x,y) =position of anchor node consider state space model of the location system Eq.6 is given by

X_K+г =A X_K              (6)

where Xk= [X ,k ,Y_tkA^T ; A =/ 2 = [J 0]

Measurement model of the system is given by Eq.7

z_k = h_k(x _k) +v_k                (7)

z_k = Actual measurement of node k.

vk = measurement noise hk(x)) = 7(xik - xk)2 + (Vik - Ук)2

H_k = Jacobian matrix of expected measurement is given in Eq.8

г______________ У1к~Ук _______i ^^k = L^^** -^k)²+ (У1к-Ук)²    J(*ik~ Хк)² + (У{к~Ук)² J    ⁽⁸⁾

• a.    Adaptive Extended Kalman Filter

In nonlinear environment EKF is used to estimate the location of nodes based on recursive equations. EKF consists of two phases time update, refinement phase viz.

• a)    Time update phase

Assume that initially no inputs are given to system.

X_K+ 1 = A Xk                   (9)

X_K =state estimation of sensor at k

XK+1 = state estimation of sensor at k+1

Predicted error covariance matrix is

P_K+ 1 = APkA^t                (10)

P K+1 = error covariance of X _{K +T}

P_K = error covariance of X _K

• b)    Measurement phase

Innovation sequence gives the difference between predicted measurement and actual measurement. Innovation sequence is given in Eq.11.

^=ZK-h(xk)(11)

Covariance of Innovation sequence is given in Eq.12.

Sk = НкРк HK + KK(12)

= Jacobian matrix of expected measurement.

Updated state vector is given in Eq.13

Xk+i = Xk + KkXK(13)

is known as kalman gain and calculated as follows in Eq.14

kk = HP KK-11

Updated state covariance matrix is given in Eq.15

Pk+i = (I - KhHk)(15)

From the Eq.13. it is observed that updated position state of nodes depends on innovation sequence. In indoor environment due to noise and multi path effects difference between estimated measurement and actual measurement is very high. Hence adapt noise covariance of innovation matrix to get accurate node positions.

Rr —* “Kk                ⁽¹⁶⁾

FIT = R 0 D = ¹-Г(^А_           (17)

^{tr (} ^vk)

• b.    PSO Assisted AKF

PSO is an optimization mechanism which works on the behaviour of group of birds. In this proposed algorithm PSO is used to tune or assist covariance of innovation sequence.

• 1.    Intialize population of particles with random position X i and random velocity v i

• 2.    Compute fitness of each particle using equation. Step by step procedure for PSO-AKF is given below

• 3.    check the following conditions for evaluations

FIT = R 0 D = ^t^ tr (Сук)

• a)    If | FIT (x i ) | < | FIT (P best ) | then P best = x i

• b)    If | FIT (x i ) | < | FIT (G best )|then G best = x i

• 4.    Velocity of each particle is given by

• 5.    Update position of each particle using Eq.

• 6.    Repeat step 2 to 5 to get required FIT = 1

• 7.    If FIT = 1 then output = G_hesl(a)

• 8. Adapt noise covariance of innovation matrix to get accurate node positions using к .

v_t = v_i + C₁x rand(  ) x rand.(  ) x (Pb-s t_i - x^

+ C₂ x acid d(   ) x (G b - s t — x^

x_t=Xi + v_tA t

^Kk —^{— K}Kk

Pseudo code for the PSO-AKF is given in Fig.1

• 1:    Deploy agent & anchor node func ( )

• 2:        Set_agent_ nodes N = 100

• 3:        Set_anchor_ nodes M = 10;

• 4:          euclidian_ distance _cal func( )

• 5:           di = V(x - X t ) ² + (У - y t ) ²

• 6    : Dtermine accurate position of nodes ( )

• 7    :        EKF Function( )

• 8:        Time update phase

^k +1 = ^A X _K

X_K = state estimation of sensor at k

X k +1 = state estimation of sensor at k+1

X k = [Х -к ХкГ      A = I₂ = g 0]

• 9:        Predicted error covariance matrix

^ к+1 = ^A K_KA ^т

Р_{к +} 1 = error covariance of Х к ₊ 1 = error covariance of

• 10:       Measurement phase

• 11:      Measurement model z_k = h k ( x) + V_k

h_k (xj = V (x_ik - x_kY + (у _lk - у k)

Jacobian matrix

Г_________xt k - xk_________ _________y tk -y k_________ k = [VCXk-XkD^Cyik-yk)2'  V(xik-Xk)2 + (yik-yk)2

• 12:         Ук 7_K  h(X))

• 13    :       Covariance of Innovation sequence

S_K = H_kP_KH^{+ +} R _K

= Jacobian matrix of expected measurement.

• 14    :      Updated state vector    Xk +1 = Х к + Kk^

• 15    :       = kalman gain =

• 16    :       Updated state covariance matrix

=( -    )

PSO-AKF function (  )

• 17:       If ROD> γ

• 18    :       Call PSO_ function ( )

• 19:                   PSO_ function( )

• 20:    Intialize_random_ position &velocity x i ,v i

• 21    :               Compute    p IT = ^t-^r^^

F                 tr(Сек)

• 22    :          if| FIT (x i ) | < | FIT (P best ) | then P best = x i

• 23:          if | FIT (x i ) | < | FIT (G best ) | then G best = x i

• 24:         v_t = v_t + C ₁ x randl.  ) x randl. ) x

(Pbest- - x_t) + C₂ x rand( ) x (Gbest - x_t)

• 25    :    x _t xX_t + v_tA. t

• 26:                  If FIT S 1 then output = G best ( « )

• 27:                   noise covariance of innovation matrix

adapt function( )

• 28:                 K^ —> ^K^

• 29:                   end if.

• 30:                   end if

• 31:         end if.

32:end.

Fig.1. Pseudo code for PSO Assisted AKF

• V.    Simulation Results And Analysis

• A.    Simulation setup

For simulation, the sensor nodes are deployed in the area of 500mX500m. In this, sensor nodes are classified as two types i.e. anchor nodes and agent nodes. Anchor nodes are known their positions primarily and agent nodes are not aware about their positions. The above deployment of sensor nodes is done using MATLAB. The transmission range of sensor node considers as 5m and initial energy of nodes is 50 Joules. The simulation parameters are also listed in Table1.

Table 1. Simulation parameters

Parameter	Symbol	Value
Network size	S	500mX500m.
Environment	E	Indoor
No.of anchor nodes	Na	12
No.of agent nodes	Na	120
Transmission range	T r	5 m
standard deviation	σ	1% of measured distance
Intial energy	E i	5 J
Transmission power (W)	P t	2
Distance of reference (m)	d o	1.2
Path loss exponent	α	2

The performance parameters used for the evolution is defined as follows.Performance of the proposed algorithm is evaluated by considering different scenarios and performance metrics. The performance metrics for analysis of results are defined below.

Cumulative Distribution Function (CDF): CDF is used to measure accuracy of localization system. If the accuracy of the two measuring systems are equal, then systems compared in terns of CDF. The system which reaches high probability values faster is considered as better system because its distance error is focused in small values.

Complexity: Average number of transmissions required to send the data from source to destination in specified intervals of time is known as complexity

Root Mean Square Error (RMSE): Difference between the estimated location value and and actual location value of localization algorithm. Equation 9 gives the formula to find RMSE value.

• B.    Results analysis

The proposed efficient localization routing tested with various parameters and results are analyzed. The proposed localization algorithm is analyzed and compared with EKF algorithm, kalman filter and least square algorithm.Fig.2 represents graph plotted for position versus CDF and results are compared among PSO-AKF algorithm, EKF algorithm, kalman filter and least square algorithm. In this least square algorithm performance is poor when compared with three algorithms. The reason is that noise and multipath effects shows impact on accuracy. The kalman filter performs better than least square method and less performance than PSO-AKF algorithm and EKF, due to KF does works well in nonlinear environment like noise, indoor environment. PSO-AKF algorithm performs better when compared with other algorithms, because of PSO assist the FIT parameter to find accurate positions.

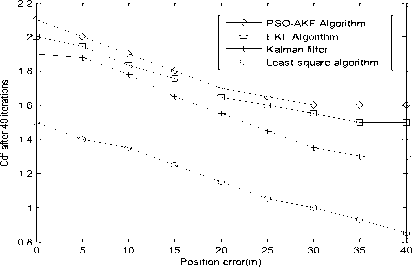
Fig.2. Performance comparison of different Algorithms by varying position error.

Fig. 3 represents graph plotted for iterations vs. avg. no. of transmissions per agent and results are compared among PSO-AKF algorithm without CRB, PSO-AKF with CRB. In this PSO-AKF algorithm without CRB performance is poor when compared with PSO-AKF with CRB. The reason is that CRB estimate lower bound of localization error and discards nodes which give inaccurate position information.

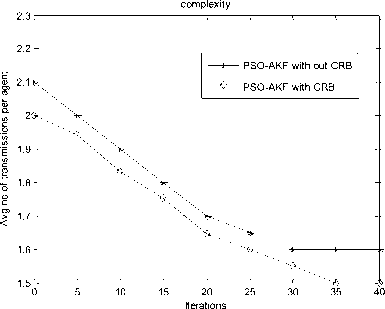
Fig.3. Performance comparison by varying number of iterations

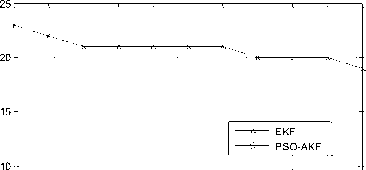
Fig. 4 shows graph plotted for time vs. ROD and results are compared among PSO-AKF algorithm and EKF. PSO-AKF algorithm performance is better than EKF because PSO is used to assist AKF.

Fig. 5 represents graph plotted for No. of iterations Vs MSE of localization error and results are compared among PSO-AKF algorithm, EKF algorithm, KF and least square algorithm. In this least square algorithm performance is poor when compared with three algorithms. The reason is that noise and multipath effects shows impact on accuracy. The kalman filter performs better than least square method and less performance than

PSO-AKF algorithm and EKF, due to KF does works well in nonlinear environment like noise, indoor environment. PSO-AKF algorithm performs better when compared with other algorithms, because of PSO assist the FIT parameter to find accurate positions.

0    200   400   600   800  1000  1200  1400  1600  1800  2000

Time(Sec)

Fig.4. Performance comparisons by varying time

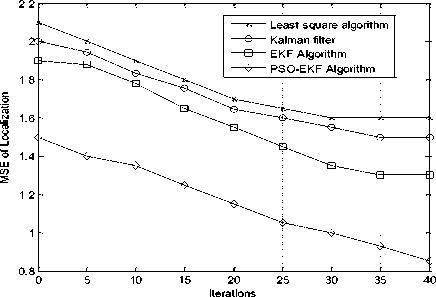
Fig.5. Performance comparison by varying number of iterations

In cooperative WSN all the agent nodes participated in the communication process. Fig. 6 shows number of anchor nodes Vs. CPU time. CPU time increases linearly as the number of anchor nodes increases. Hence select optimum references using CRB.

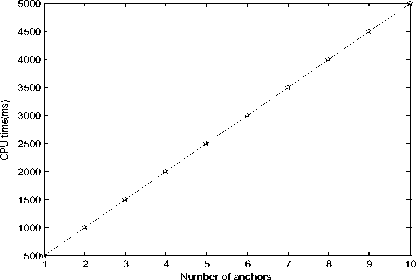
Fig.6. Performance comparison by varying number of anchor nodes

In a cooperative localization of WSN agent nodes also participated in localization process. Fig.7 shows the number of anchor nodes vs. location error. From the results it is observed that number of anchor nodes are less, location error is more. If number anchor nodes increase, location error decreases but complexity increases. At one particular point number of anchor nodes are more than 4 location error is same. Hence consider 4 anchors as optimum references.

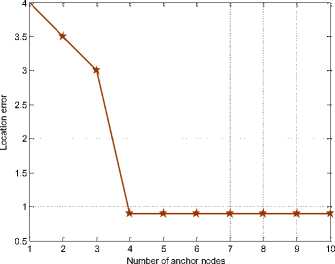
Fig.7. Performance comparison by varying number of anchor nodes.

The PSO tuned AKF algorithm performs better in comparison with other four algorithms. The reason is that proposed algorithm finds accurate nodes locations.

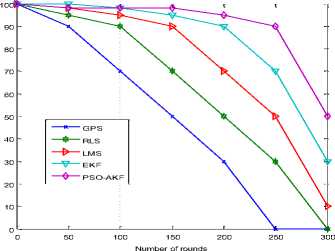
Fig.8. Number of rounds vs. residual energy

Fig.8 shows a graph plotted for number of rounds vs. residual energy, results are compared among PSO-AKF, EKF, DRLS, DLMS and GPS in terms of residual energy. The performance of GPS is deprived in comparison with other four algorithms because of GPS is complex, consumes more power hence nodes died early. DRLS algorithm performs poor in comparison with DLMS, EKF and PSO-AKF because it is more complex and consumes more power. In this algorithm nodes died in 300 rounds. DLMS performs better in comparison with DRLS and GPS because it is less complex. Residual energy of nodes gradually decreased and 10% of energy remains at 300 rounds. EKF algorithm performs better in comparison with other algorithms because of less computational complexity. Residual energy of nodes gradually decreased and 30% of energy remains at 300 rounds. The PSO-AKF algorithm performs better in comparison with other four algorithms. The reason is that PSO-AKF, MSE is least and computational complexity is low. Hence residual energy of nodes improved.

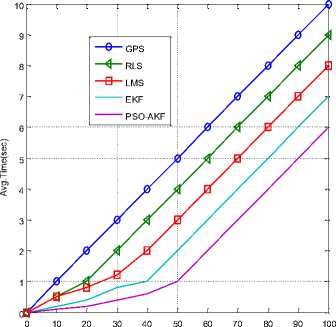
Number of nodes

Fig.9. Number of nodes Vs. average time

Fig.9. shows graph plotted for number of nodes Vs. average delay and results are compared among PSO-AKF, EKF, DRLS, DLMS and GPS. Delay of network is increased with increasing number of nodes. The avg. delay of GPS is more when compared with other four algorithms because of GPS is more complex and requires more processing time. Avg. delay of DRLS algorithm is more in comparison with PSO-AKF, EKF and DLMS because of DRLS is complex in comparison with other algorithms. DLMS algorithm gives more avg. delay in comparison with EKF and PSO-AKF because of its SNR and stability is low. Avg. delay of DLMS is less in comparison with DRLS and GPS because it requires fewer computations. PSO algorithm gives less avg. delay in comparison with DRLS, DLMS and GPS because it is less complex, hence processing time is reduced. PSO-AKF algorithm gives least avg. delay in comparison with EKF, DRLS, DLMS and GPS because its computational complexity and MSE is least.

• VI.    Conclusion

In this paper, Enhanced localized routing in WSN using Particle Swarm Optimization assisted Adaptive Extended Kalman Filter (PSO-AKF) is proposed. To study the performance of proposed method, simulation study was conducted with various conditions. The proposed algorithm is compared with GPS, LMS, RLS, EKF and PSO-AKF. From the comparison result it was found that PSO-AKF performs better than other algorithms in terms of complexity, MSE and residual energy.

Acknowledgements