Enhancement of S13 Quantum Key Distribution Protocol by Employing Polarization, Secrete Key Disclosure and Non-repudiation

Web security relies on the computational complexity related with the generation of the secret key. This is not enough due to the fast growing approaches to calculate the secret key that cannot be cracked [1]. Public key cryptography was the first solution to key distribution problem. It is among the theoretically breakable computational security solutions because they rely on computationally challenging mathematical problems and assumptions about the computing capability of potential adversaries. As a result, they are in danger as computer power grows and new quantum computing algorithms are developed that can solve some commonly used, computationally demanding mathematical problems in polynomial time [2. 3]. Currently, the quantum cryptography is the most practical resolutions for information security systems that present the ultimate approaches for key distribution. It can allow the exchange of secret keys between users connected using a medium that is vulnerable to eavesdropping [4, 5].

The Quantum key distribution (QKD) security is ensured by the principle of quantum mechanics and the evolving maturity of QKD devices and technologies makes QKD start to becoming widely used [6].

To understand QKD first move away from the traditional key distribution approach of Haliru sending key information to Maryam. Instead, make use of a more private starting point, in which Haliru and Maryam originally create their own, secret independent random binary number sequences. These number sequences having many bits than they require for the key information they will ultimately share. They will usually do a bit-wise comparison of these sequences of binary numbers to identify a shared random subset that will be the key material. And in a situation that attackers are detected with high probability [7]. They use a quantum transmission over a quantum channel and a discus the results over a public channel [5].

It is necessary to appreciate that Haliru and Maryam do not need to identify all of their shared binary numbers or even specific ones; because the only requirements on the key information are that the numbers should be secret and random. QKD does not remove the need for other cryptographic primitives, such as authentication and access control, but it can be used to build systems with new security properties. But, the main challenge that limits its widespread implementation is the low availability and high cost of dedicated fiber equipments [8].

The initial BB84 quantum key distribution protocol which is the raw key exchange of S13 quantum key distribution has weakness of disclosure of large portion of secrete key or eavesdropping [9]. These possibilities expose that for each transmitted qubit, there is 75% probability that Eve's act goes unnoticed. Also, it cannot make use of most of the generated random bit. It can just utilize about 40%–50% of the generated bits [10].

This paper enhanced S13 quantum key distribution protocol by combining polarization, secrete key disclosure, biometric and MAC address to resolve the above mentioned problems. The row key exchange part of the S13 quantum key distribution is enhanced by employing polarization techniques to make use of most of the generated random bits. Then, the final key generated at the end of Error Estimation phase would be divided into blocks, padding, inverting the last bit of each block and XORing the block thereby generating a totally different key. Additionally, the random bits x by Haliru or Server in some cases and random seed string x x ... x by either Maryam or Haliru, or Maryam or Sever will be from biometric or serve MAC address respectively. The enhanced S13 quantum key is analyzed using cryptanalysis and the results of analysis shows that the enhanced protocol ensures disclosures of large portion of secrete key to prevent eavesdropping, utilization of most of the chosen binary strings to generate strong key and safeguarding against impersonation attack.

The contributions of this research are as follows:

• 1)    Polarization, blocks and XORing is combined to eliminate the weakness of disclosure of large portion of secrete key and allow utilization of large portion of generated bits for key generation.

• 2)    Biometric or serve MAC address is employed as the random seed of S13 quantum key distribution protocol to ensure security against impersonation attack.

2.    Related Works

The rest of this paper is organized as follows. Section two is review of related works, section three is discussion of BB84 quantum key distribution, section four is discussion of S13 quantum key distribution, section five is limitations of S13 quantum key distribution, section six is the enhances S13 quantum key distribution, section seven is evaluation of the enhanced S13 quantum key distribution and section eight is conclusion.

Guskind and Krawec in [11] proposed a fresh mediated semi-quantum key distribution protocol. The former work is extended that provide great efficiency. This is a solution to key distribution problem. Their modification allows fully deployment of every quantum signals. There difference between their work and previous works is that raw key bits may be generated in respective of the server’s message and can allows flip his raw key bit by Bob if the server transmit the message ‘2’ or ‘3’. But if care is not taken on this flipping option, the correlation may be destroyed thereby creating more errors in the raw key.

Xu et al. in [11] introduced a device independent QKD protocol to solve key distribution problem with random post selection. In their scheme the extraction of secrete keys is only from the outcomes of post-selected subsets. This could not disclose the loopholes of detection as far as the post-selected entropy is evaluated from the entire data. But it has high errors even though it will not summon detection gaps. They proved their defense against collective attacks and also reduce the information cost of error correction has been illustrated as the result of the post selection. They therefore facilitate the improvement of loss tolerance.

Wang et al. in [13] studied quantum key distribution problem in respect of the construction of BB84 and proposed a new quantum key distribution scheme consisting of two steps. This is an enhancement of quantum key distribution protocol. Step one involving unidirectional channel 1 for quantum and step two involving classic bidirectional channel 2 for general information. It can be employed to improve the security of the key distribution scheme because every two cases give different test results. Theoretical analysis was carried out to express the advantage of the given QKD scheme.

EBB84 protocol is more secure but it takes little longer time than BB84 protocol.

Kumar et al. [14] attempt to enhance the security of QKD by increasing the size of the key shared between two parties. Even if attacker is successful in getting the initial authentication keys, the extracted keys from the both sphere of the proposed QKD scheme ensures unconquerable security. Their result shows that the proposed protocol is getting to 75% of efficiency.

Abdullah et al. in [16] proposed a new method of encoding a stream of bits into polarized photons using Legendre Symbol called MBB94. Here, both of the sender and the receiver agree by means of the function of Legendre symbol. They use only quantum channel and so the efficiency is high. .

Saha et al. in [9] enhanced BB84 Protocol by solving disclosure of large portion of secret key or attacker dipping problem which may perhaps not be detected. Therefore, the shared secret key will be strong enough to use in secret communication even if presence of attacker is not detected. Phases of the existing BB84 algorithm along with the customized one is described in detail with example and pseudo code. Due to extra operations performed including block division, padding, inverting of last bit of each block and XORing will add computational overhead to the enhanced scheme.

Trushechkin et al. in [17] consider a class of prepare-and-measure QKD protocols, utilizing additional pseudorandomness in the creation of quantum states. They merge classical pseudo randomness with quantum encoding of data and express that, for single-photon sources, the considered protocol gives better secret key rates than the BB84 and the asymmetric BB84 protocols. The proposed scheme enables averting of shifting operation but half of the key is lost.

Meslouhi et al. in [18] proposed a new protocol called “QKDPRB” based on random bases. It allows selection of infinite number of bases as an alternative of two bases. It involves use of standard encoding bases moving circularly with a variable rotational angle α which depends on angular velocity ω(t). This turns traditional bases into relative ones. They verified a universal security proof where they confirmed the minimum security level guaranteed by QKDPRB. They also confirmed that the proposed protocol is the same as a perfect random channel where attacker gained the lowest possible mutual information.

Ahonen et al. in [20] proposed and investigate a quantum key distribution protocol based on sending entangled N-qubit states as an alternative to single-qubit ones as in the trail-blazing scheme by BB84. Their outcomes show that entanglement can be applied to significantly enhance the BB84-type key distribution, even in the case of two-qubit entanglement. This protocol can be straightforwardly adapted to the several variants of the BB84 scheme. Regrettably, loss of qubits may create a problem not only for attacker, but also for legitimate user. This protocol cannot be suggested for use at extreme distances where most transmitted qubits are lost because if one of the entangled qubits is totally lost, the quantum bit error rate (QBER) of the remaining qubits is likely to increase.

3.    BB84 Quantum Key Distribution (QKD) Protocol

Bennett and Brassard proposed BB84 in 1984 [22]. It was the first employment of quantum physics in information and communication theory that initiate the explosive study of quantum communication and cryptography.

The BB84 protocol proceeds as follow [23]:

• 1)  Haliru produce two strings X_H = X_HiX_H....x^ and y_H = УнгУн 2-- Урт of random classical bits.

• 2)  Haliru make use of x and y to form a quantum state as a tensor product of N qubits.

I ^)⁼^ k =_l\ ^ x_HKy_H J,                                           ⁽¹⁾

HK HK where ^хкУк depends on the values of X^ and y^

I ^ 00 H0),                                                   (2)

| ψ 10 〉 = |1 〉 ,

| ψ 01 〉= | +〉= ^{|0 〉+ |1 〉}

| ψ 11 〉 = | - 〉 =

|0 〉 - |1 〉

Really, the string yH is used to choose between the bases of the operators Z({| 0),| 1)}) and X({| +),| -)}), and the string x is used to attach the distinct qubit in the basis.

• 3)    Haliru transmits the sequence of qubits to Maryam through the quantum channel.

• 4)    Maryam accepts the qubits and perfoems measurement on the qubits using either the basis X or Z for each qubit according to a randomly generated sequence y . The measurement x results in a bit value 0 (1) if the measurement correlate with the positive (negative) eigenvalue of X or Z. Maryam then make public that she received the qubits through the public classical channel.

• 5)    If Maryam’s measurement basis is the same as Haliru’s preparation basis, Maryam’s measured bit value in x

will be the same as Haliru’s bit value in x . If the bases are different because the basis sets X and Z are mutually unbiased then Maryam’s resulting measured bit value will have a probability of 0.5 being correct. Haliru makes public the string y in the classical channel to decide whether they use the same set of bases.

Haliru and Maryam debate through the classical channel to discard those bits in x and x that the preparation basis by Haliru and the measurement basis by Maryam are not the same..

For every remaining bits in x (called the sifted key x' ), Haliru’s preparation basis and Maryam’s measurement basis are the same. If no errors are experience in the qubits during the transmission in the quantum channel, Maryam’s measured states for those qubits should give rise to bit values x' matching the bits in x' , i.e., xH'14 xM'

However, it is very likely that errors experienced in the qubits during the transmission. Haliru thus selects a subset of x' and tells Maryam which bits are selected through the classical channel.

Haliru and Maryam check the values of the selected bits through the classical channel. If the quantum bit error rate (QBER) r in those bits is higher than a threshold, the protocol is terminated. If not, they proceed to the next step. The threshold is aborted by the security analysis that makes sure privacy amplification can be carried out.

Haliru and Maryam carry out error correction and privacy amplification through the classical channel

4. S13 Quantum Key Distribution Protocol

S13 [24] protocol is a new quantum protocol. It is actually identical to the BB84 protocol for all the quantum manipulation. The only difference is that it uses private reconciliation from a random seed and asymmetric cryptography, and it can be implemented in the existing devices without modification [25]. As such, it allows the generation of larger secure keys.

So, Haliru and Maryam exchange a set of encoded photons according to four states | 0 〉 ,| 1 〉 ,| +〉 ,| -〉 , which convene establishing two basis with orthogonal states β = {| 0 〉 ,| 1 〉 } and β = {| + 〉 ,| - 〉 } , where | _±〉 ₌ ¹ (| ₀ 〉_± | ₁ 〉 ) . Coding the 2

binary value 0 to the states |0 〉 and | +〉 , and the binary value 1 to the states |1 〉   and | -〉 . Which is denoted by

ψ ₀₀ ≡ |0 〉 , ψ ₀₁ ≡ |1 〉 , ψ ₁₀ ≡ | + 〉 and ψ ₁₁ ≡ | - 〉 for simplicity.

The protocol consists of such activities [24] as raw key exchange, random seed, missing key exchange, asymmetric cryptography and private reconciliation

• 4.1    Row Key Exchange

• 4.2    Random Seed

The raw key exchange is the same as BB84.

• 1)    Haliru or Maryam publishes a random binary string ww ... w .

• 4.3    Missing Key Exchange

• 1)    Haliru sums x ⊕ w , k = 1,2,3,…,N. Getting a sequence of binary basis tt ... t  and generates other random

string of binary values j j ... j that will match to other key that he wants to exchange with Maryam. Haliru gets the coupled state | ψ 〉 and sends it to Maryam through a quantum channel from the elements k that is occupying a concrete position of the preceding strings

• 2)    Maryam sums (1 ⊕ x ) ⊕ w ,k = 1,2,…N. Getting the string of binary basis n n ... n  and measures each received

• 4.4    Asymmetric Cryptography

state | ψ 〉 with the matching base β generating the string bb ... b .

tkjk                                       nk                                12

Haliru and Maryam interchange a set of binary strings and apply in different binary arrangements the function У defined as follows:

f(x, y, z):= {xy,,zz==10

• 1)    Haliru sums t ⊕ j ,k = 1,2,…,N. Getting the binary string y y ... y that sends to Maryam.

• 2)    Maryam encrypt x in u and v with

uk =nk ⊕ f(xMk,ak,bk⊕yk),(7)

vk =nk⊕f(xMk,bk,ak⊕yk)

K = 1,2,…N. Getting the public string u u ... u y vv ... v that it sends to Haliru.

• 3)    Haliru sums t_k ⊕ f ( x_Hk ,(1 ⊕ y_Hk ) ⊕ u_k , j_k ⊕ v_k )

• 4.5    Private Reconciliation

Decrypting m for k = 1,2…N. getting the private string x x ... x of Maryam.

• 1)    Haliru contrast the strings x x ... x and x x ... x , sending to Maryam the binary sequence ll ... l with

lk =xHk ⊕xMk(9)

• 2)    Maryam sums x⊕l, k = 1, 2, ...,N. getting the private string x x ...x of Haliru and apply:

5.    Limitations of S13 Quantum Key Distribution

• 5.1    Disclosures of large portion of secrete key or eavesdropping and non utilization of most of the generated bits.

f(lk,ak,bk ⊕yk)≡ik(10)

f(lk,ak,yk⊕bk)≡jk(11)

k.= 1,2,3,…N getting the private strings of Haliru y y  ... y  , y j 1 j 2... jN

This section highlights the limitations of S13 quantum key distribution. These include disclosures of large portion of secrete key or eavesdropping, non utilization of most of the generated bits and impersonation attack. These limitations are discussed in the following sub-sections of this section.

The initial BB84 quantum key distribution protocol has weakness of disclosure of large portion of secrete key or eavesdropping [9]. The key can be derived with the presence of an eavesdropper Eve as follows [26]:

• 1)    Eve chooses the wrong basis: x=x→ qubit is distorted

• 2)    Maryam chooses correctly: x=x→ Eve introduces 50% error probability

• 3)    Maryam chooses incorrectly: x=x→ random result, Eve is not detected.

• 4)    Eve chooses the correct basis: x=x→ qubit is not distorted.

• 5)  Maryam chooses correctly: X_M = X_H ^ Eve is unnoticed and has one bit of the key.

• 6)  Maryam chooses incorrectly: X_M = X_H ^ random result, Eve is not detected.

• 5.2    Impersonation attack

6.    Enhanced S13 Quantum Key Distribution

• 6.1    Enhanced S13 Quantum Key Distribution Steps

These possibilities expose that for each transmitted qubit, there is 75% probability that Eve's act goes unnoticed.

Also, BB84 protocol cannot make use of most of the generated random bit. It can just utilize about 40%–50% of the generated bits [10] .

An impersonation attack is an attack in which an attacker successfully assumes the identity of one of the legal users in a system or in a communications protocol. As seen earlier attacker Eve can chooses the wrong basis: Xe = Xh ^ thereby distorting the qubit and making attacker unnoticed. So, the attacker can impersonate Haliru such that Maryam will see the attacker as Haliru.

Also, if the random binary string x x ... x published by either Haliru or Maryam during random seed stage of S13 protocol is stolen by Eve, Maryam or Haliru can impersonated.key from the tentative one. Also, the random bits x _H by Haliru or Server in some cases and random seed string x x ... x by either Maryam or Haliru, or Maryam or Sever will be from biometric or serve MAC address respectively.

In this section, we enhance the S13 quantum key distribution. The row key exchange part of the S13 quantum key distribution which is the same as BB84 is enhanced by employing polarization techniques to make use of most of the generated random bit and add an extra phase of security in order to enable generation of secure key. The extra phases of security are division of the final key into blocks, padding, inverting the last bit of each block and XORing the block to generate a totally different key from the tentative one. Also, the random bits x _H by Haliru or Server in some cases and random seed string x x ... x by either Maryam or Haliru, or Maryam or Sever will be from biometric or serve MAC address respectively.

The enhanced S13 quantum key distribution also consists of five (5) steps namely: row key exchange, random seed, missing key exchange, asymmetric cryptography and private reconciliation. These are discussed as follows:

• 1)    Raw Key Exchange

Raw key exchange which is initially BB84 is enhanced by employing polarization techniques to make use of most of the generated random bit and add an extra phase of security in order to enable generation of secure key and one of the random seed of Haliru or Maryam will be from their biometric and that of Server in some cases will be from Server MAC address. This can be express as follows:

• a.  Haliru chooses random n-bits string S _Hi = s _H1 s _H2 ^ s _Hn and polarization of the i-th bit p i — p¹ p ²... pⁿ .

• b.  Haliru creates and generates the corresponding photons into one of four states as following | ^ ., p i ) related to the

bit information of B_H and polarize P where 1 <  i <  n .

• c.    If S_H. — 0 S_Hi = 0, then P^l is encoded to diagonal basis and if S_H. — 1, then P^l is encoded rectilinear basis based on the encoding process as follows:

  | ^ c , '>  ^ 1 +)-^ к, ->-m ->-i | ^ 1 , +) - ^ - | 0 ) - ^ 1^, —M- |1 )-^-

  -4i°)+ ii )|                                     (12) J 2      J [ 72m1>)                        (l3) ||+>+ | ->1                                  (14) 72        J -f= 1 +)- 1 -)1                                        (15) 72        J

  
  
  
  
  
  
  
  

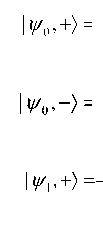
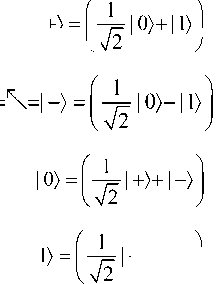
• d.    Then, Haliru transmits photons to Maryam in sequence over a quantum channel.

• e.    On the other receiving the photons side, Maryam polarization are p' = p¹ p ²... p n for 1 <  i <  n . If P = | +) or P = | —) then S_Mi = 0 , if P = | 0 ) or P = | 1 ) then S_Mi = 1.

• f.   Then the n-bit string for Maryam is S_M. = S_mS_{M 2}... S_Mn , which is the final key

• g.  Haliru and Maryam both must have to agree with a number of bits in each block ‘n’ because the n-bit must be

divided into blocks. If the key is not completely divisible by ‘n’ then Padding is required for equally division of blocks.

• h.    If the last bit is 0, then change that to 1 and if it is 1 then changed that to 0. That is, inverted. This will further confuse the attacker.

• i.    Now keep the first block remain same. Then XOR the next block with the first block and store the result. After that, XOR the next block with the result of the previous block and store the result. This process will continue up to the last block.

• j.    Final key will be generated by sequentially puting each block where the result of XORing is stored from the first one

• 2)    Random Seed

• a. Haliru or Maryam provide a binary string from their biometric b_H,= b_mb_{H 2}... b_H„ and b_M[ = b_Mp_M2-b>_M„ respectively. Or if the communication is with the server, a binary string from server MAC address mc = mcmc₂ ... mc_n .

• 3)    Missing Key Exchange

• a.    Haliru sums s_{h t}© b_Hk , k = 1,2,... n . Obtaining a sequence of binary basis t^ ... t_n . Haliru generates the corresponding photons into one of four states as following | ^ , P_H ) related to the bit information of t_t and polarize P_H where 1 <  i <  n using equations (12) to (15) and sends it to Maryam through a quantum channel.

• b.    Maryam sums (1 © s_m)) © b_M, , k = 1,2,... n . Obtaining the string of binary basis nn₂ ... n_N and then decode the received photons. That is, If P_H = | +) or P_H = | —) then S_u. = 0 , if P ' = | 0 ) or P = | 1 ) then S_M. = 1 generating

the string mm ... m .

• 4)    Asymmetric Cryptography

Haliru and Maryam exchange a set of binary strings and apply in different binary arrangements the function fdefined as follows:

f (x, y, z ):={ yz0

• a.    Haliru sums S_Ht © t_k s _Hk ®t _k , k = 1,2,... N . Obtaining the binary string y_x y ₂... Ух that sends to Maryam.

• b.    Maryam encrypt s in u and v with

uk = nk © f (SMk , nk, mk, ©Ук ), vk = nk © f (sMk, mk, nk, ©yk)

Where

Ъ = 1© Ъмк © SMk(19)

• c.    Haliru sums t_k © f ( S Hk ,(1 © ' k ) © U k , Jk , V k )

'k = SHk © SMk

• 5)    Private Reconciliation

• a.    Haliru compares the strings s s ... s and s s   ... s   , sending to Maryam the binary sequence ll ... l

with lk = sHk ф sMk

• b.    Maryam sums s^ ф l_k, k = 1, 2, ...,N. Obtaining the private string s_Hls_H....s_HN of Haliru and apply:

7.    Evaluation of the Enhanced S13 Quantum Key Distribution

• 7.1    Utilization of Most of the Chosen Binary Strings to Generate Strong Key

• 7.2    Disclosure of Large Portion of Secret Key

• 7.3    Security against Impersonation Attack

8.    Conclusion

f (lk , nk , mk ф Ук ) = sHk

f(lk,nk,Ук фmk) ^ tk к = 1,2,...N. Obtaining the private strings of Haliru sH1 sH2 ■■■ sHN

In this section, we evaluate the security of the enhanced S13 key distribution protocol using cryptanalysis. The security of the enhanced protocol is based on disclosures of large portion of secrete key to prevent eavesdropping, utilization of most of the chosen binary strings to generate strong key and safeguarding against impersonation attack.

The size of the key is one of the most important factor for determining the strength of a key. Sharing of secret key between Haliru and Maryam without using classical channel will ensure utilization of most of the key generation information. This work employs polarization technique unlike in the BB84 QKD protocol. In the enhanced protocol, Haliru creates and generates the corresponding photons into one of four states as following \^ _Ht P¹} related to the bit information of B_H and polarize P where 1 <  i <  n , encode and sends the corresponding bits to Maryam via quantum channel. On the other receiving the photons side, Maryam polarization are p‘ = p¹ p ²... pⁿ for1 <  i <  n . If p‘ = | +) or p i = | -) then S_M = 0, if pⁱ =| 0 ) or p i = | 1 ) then S_u( = 1. This is the key to be shared by them.

This is ensured by providing some phase of securities after error estimation of raw key exchange of the S13 quantum key distribution protocol which are not previously available in the S13 QKD protocol. In the enhanced protocol, the tentative final key generated at the end of error estimation phase should be divided into blocks. So, Haliru and Maryam must have to agree with ‘n’ number of bits in each block. If the tentative final key is not completely divisible by ‘n’, then Padding is required for dividing the blocks equally. The last bit of each block is inverted followed by XORing. Here, the first block is remain the same, then XORing the next block with first block, the XORing the next block with the first result up to the last bock. These will result in disclosure of large portion of the secrete key.

An impersonation attack is an attack in which an adversary successfully assumes the identity of one of the legitimate parties in a system or in a communications protocol. Here, the random bits b b ... b by Haliru or mc mc ... mc by Server in some cases or random seed string b b ... b by Maryam will be from biometric or serve MAC address respectively. These are hard to copy and share, cannot be forgotten or easily guessed and is hard to forge or distribute. This also ensures non-repudiation unlike in S13 quantum which used binary numbers as the random bits.

Information security depends on the computational complexity involves in generating the secret key which is not enough as the fast growing methods to calculate the secret key that cannot be compromise. The initial method for resolving the key distribution issue was public key cryptography. Because they rely on computationally difficult mathematical issues and presumptions about the processing power of prospective adversaries, it is one of the theoretically breakable computational security methods. They consequently face risk as computing power increases and fresh quantum computing techniques are created that can quickly solve some widely utilized, computationally challenging mathematical problems. The most realistic solutions for information security systems right now that offer the best key distribution strategies are provided by quantum cryptography. It may enable users connecting over a channel that is susceptible to eavesdropping to exchange secret keys. Currently, the quantum cryptography is the most practical solution for information security systems, which presents the ultimate method for key distribution. The initial BB84 quantum key distribution protocol which is the raw key exchange of S13 quantum key distribution has weakness of disclosure of large portion of secrete key or eavesdropping. These possibilities expose that for each transmitted qubit, there is 75% probability that Eve's act goes unnoticed. Also, it cannot make use of most of the generated random bit. It can just utilize about 40%–50% of the generated bits. This paper enhanced S13 quantum key distribution protocol by combining polarization, blocks and XORings with biometric and MAC address to resolve the problems mentioned above. The row key exchange part of the S13 quantum key distribution which is the same as BB84 is enhanced by employing polarization techniques to make use of most of the generated random bit. Then, the tentative final key generated at the end of Error Estimation phase should be divided into blocks, padding, inverting the last bit of each block and XORing the block to generate a totally different key from the tentative one. Also, the random bits xH by Haliru or Server in some cases and random seed string x1x2 ... xN by either Maryam or Haliru, or Maryam or Sever will be from biometric or serve MAC address respectively. The enhanced S13 quantum key is analyzed using cryptanalysis. And the results of the analysis shows that the enhanced protocol ensures disclosures of large portion of secrete key to prevent eavesdropping, utilization of most of the chosen binary strings to generate strong key and safeguarding against impersonation attack.