Ensemble feature selection algorithm

Published Online January 2019 in MECS

Today the volume and complexity of data is continuously growing, which has presented a serious challenge to the existing machine learning techniques. Data with extremely high dimensionality not only incurs insupportable memory requirements and high computational cost in training, but also affects the generalization ability of algorithms because of the “curse of dimensionality” issue [1].

Feature selection is one of the important techniques widely employed for reducing dimensionality. It aims to choose a small subset of the relevant features from the available ones according to certain relevance evaluation criteria, which usually leads to a better learning performance (e.g., higher learning accuracy for classification), lower model error and better model generalization.

Feature selection techniques are categorized into supervised, Semi-supervised and unsupervised feature selection according to whether a given dataset is labelled or not [2]. In this paper we will focus on the first category (supervised feature selection) which can further be categorized into Filter, Wrapper and Embedded.

Filter category [3] relies on measures of the general characteristics of training data such as distance, consistency, dependency, information, and correlation. Moreover, it carries out the feature selection process as a preprocessing step with the independence of the induction algorithm. This model is advantageous for its low computational cost. Relief [3], Fisher score [4] and Information Gain based methods [5] are among the most representative algorithms of the filter category.

Wrapper model [2] involves a learning algorithm as a black box and consists of using its prediction performance to judge the relative importance of feature subsets. In other words, the wrapper category uses the learning method to evaluate each subset of features. However, this interaction with the classifier tends to give better performance results than Filters. Still, these methods are very expensive to run for data with a large number of features. The most known wrapper algorithms are forward selection, backward elimination, stepwise selection, and others [6,7].

Embedded category [2] performs feature selection during the construction of the model. This approach is able to capture patterns in data at a lower computational cost than wrappers. The most common types of embedded feature selection methods are: first, regularization methods such as LASSO [8], Elastic Net [9] and Ridge Regression [2]. Second, Pruning algorithms, they use all features to train a model. Then, they eliminate features with null coefficients, while maintaining the model performance. The well-known pruning algorithm is recursive feature elimination [10].

In this paper, we propose a new feature selection algorithm based on ensemble selection from libraries of models where each model is trained using only one feature. The main idea of this paper is to select an optimal ensemble of models from the library that optimizes a given metric. Since each model corresponds to exactly one feature, the subset of selected models corresponds to the subset of optimal features.

First, for each feature we train different models using different classification algorithms and different parameter settings. The set of all models represents our library of models. Second, we use a selection with replacement technique to find the optimal subset of models that when averaged together yield excellent performance.

• A.    General Ensemble selection framework

The main contribution of this paper lies in the proposed ensemble feature selection algorithm. We use selection with replacement algorithm to extract and select the well performing ensemble of all models. We add to the ensemble models from the library that maximizes the ensemble’s performance on validation set.

As we have mentioned, the ensemble of models is selected by maximizing its performance on the validation set. However, its performance is determined by its ability to perform well on unknown datasets (test set). In this situation, overfitting occurs as a serious problem. Moreover, the corresponding performance on the test set does not always increase as indicated in [11]. This issue leads us to propose the next contributions to improve the ensemble selection.

• B.    Ensemble selection improvement

Two solutions are suggested to reduce overfitting problem and improve ensemble selection.

• 1.    We used Multi-bagging technique introduced by the authors of [11]. The idea is to select multiple groups (bags) of models randomly from the library. Then, the ensemble selection is done inside each bag. Finally, the returned ensemble is the merging of sub-ensembles returned by each bag. Thanks to this technique, there is no need for validation set.

• 2.    We used a technique called dropout .  This

technique is a regularization method. It is recently proposed for training deep neuron networks which contain multiple non-linear hidden layers [12]. In this contribution, we propose three versions of dropout: Model dropout, instance dropout and Combined dropout. 1) The key idea behind Model dropout is to randomly drop models out from the ensemble during the selection process. 2) In this version we drop out instances instead of models during the selection  procedure.3)  Combined dropout is the combination of the model dropout and instances  dropout.  With dropout, cross validation and/or splitting data into (train+validation) may be dispensable. Moreover, this technique reduces the co-adaptation between features and instances.

The rest of this paper is organized as follows: section two presents the related works. Section three is devoted to the problem and the proposed algorithms. In the fourth section, we list the results of our algorithms. As to the last section, it is put forward to conclude this work.

• II.    Related Works

• A.    Ensemble selection

  Ensemble selection is a popular ensemble learning strategy given its excellent predictive performance concerning various problems. Ensemble selection is a method of constructing ensembles from a library of generated models. Many methods have been proposed to generate diverse and accurate set of models. The most popular methods are the following: Bagging [8] creates many random sub-samples from the original dataset with replacement. This means that we can select the same value multiple times). Then we train models of one type (e.g. Decision tree) using generated sub-samples. Boosting [13] generates more accurate and diverse set of models, because it starts by predicting original data set and gives equal weight to each observation to force new models so as to attend to those observations that are hard to classify correctly. In [11], the authors create a library of 2000 models of each problem using different algorithms and many parameter settings for each algorithm.

• B.    Ensemble selection improvement

The main problem that arises when the library contains huge number of models is overfitting. The authors in [11] have proposed three additions to the simple selection process (simple forward selection) to overcome this issue. The first addition is selection with replacement, which means models can be chosen several times. The second addition is sorted ensemble initialization, where instead of starting with an empty ensemble, the ensemble is initialized by the N best models. The third addition is bagged ensemble selection, where bags of models are generated randomly from the library, then we select models from those bags.

The problem of how much data should be used for the hill-climb set has always been of interest in ensemble selection algorithms. In order to deal with this, the authors of [14] have proposed three variations of bagging ensemble selection. In the first variation, the size of data used for hill-climb set is up to the user. In the second variation, the authors used the out of bag instances as hillclimb set. In the third version, single best model is selected at each bagging iteration.

The overfitting problem is a serious issue in deep learning as well. Deep neural nets are a powerful machine learning which contain a huge number of multiple-nonlinear hidden layers and large number of parameters. This makes neural network models learn very complicated relationships between inputs and outputs. Since this results in the problem of overfitting, many techniques have been proposed to mitigate its effects. The authors of [12] have proposed what is called dropout technique to prevent overfitting in neural networks. The units are randomly dropped out from the neural networks during training as shown in figure1 of the paper [12].

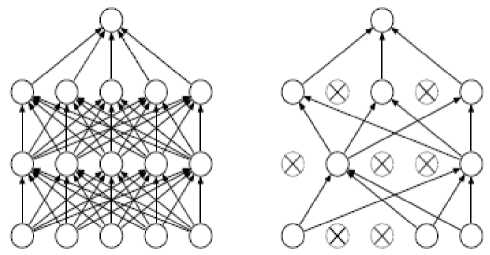
(a): Standard Neural Net             (b): After applying dropout

Fig.1. Dropout technique Reprinted from (12)

In the next section, we will describe in details the general ensemble selection framework and the proposed solutions to improve the ensemble feature selection.

• III.    Ensemble Features Selection

This section is composed of two parts with the first one describing the ensemble selection framework and the second discussing the solutions proposed to improve the ensemble selection.

• A.    Ensemble selection framework

Ensemble selection is a method used to construct an ensemble from a library of models. The first step is building a library of models using different classifiers and parameter settings. The second step is the construction procedure of the ensemble. The selection without replacement algorithms such as simple forward selection described in [11] selects a well performing ensemble of models. This procedure works as described in the following steps:

• 1.    Start with an empty ensemble.

• 2.    Add to the ensemble the model in the library that maximizes the ensemble’s performance on validation set.

• 3.    Repeat Step 2 for a fixed number of iterations or until all the models have been examined.

• 4.    Return the subset of model that yields the best performance on the validation set.

Adding models to the ensemble is done by averaging their predictions with the already selected ones. This kind of algorithm without replacement can select each model just once. This means that all the selected models in the ensemble have the same weight, which is equal to 1. In other words, the selected models have the same importance. Yet, we should bear in mind that this is not always the case. The simple forward selection is fast and effective but it is sometimes prone to overfit on the validation set especially when the number of instances is small [16].

The ensemble’s performance using simple forward selection improves as the best models are added to the ensemble. Then it starts dropping when there are just the worst models left in the library. This problem is reduced by using the selection with replacement algorithm where each model can be selected to be in the ensemble more than once.

The selection with replacement technique means that each time we pick a model, we put it back in the library. We prefer using this technique over all models selection without replacement in order to reduce overfitting problem. In this technique, once the model is selected, its weight increases. The selection process stops depending on its performance on the validation set.

Before starting the selection process, the algorithm initializes the weight of each model at zero. Then, we start the selection process of models, and we add to the ensemble only the models that when averaged together with those in the ensemble maximize the ensemble performance on the validation set. Models can be selected multiple times because each selected model is put back in the library. This step is repeated until no model can produce a notable increase in the ensemble performance. Finally, the weight of each model is returned, and features are sorted according to their weight.

The following steps give a more precise description of the algorithm of selection with replacement:

Algorithm 1: ENSEMBLE SELECTION WITH REPLACEMENT STEP 1: Ensemble initialization.

We initialize the weights of the models at zero.

STEP 2: Repeat until all models in the library are used.

Add to the ensemble the model that when averaged together with models in the ensemble maximizes the performance of the ensemble. Then the weight of the corresponding model is incremented.

STEP 3 : Return weights.

The algorithm output is a dictionary of models and their weight, and the best models are the ones with the highest weight.

Partitioning the available data into (Train+validation) can work well to test the selection with replacement algorithm and deal with the overfitting problem, but this is not always the case because:

• ■    The performance maximization on validation set does not necessarily mean that the selected ensemble will not overfit on other datasets.

• ■    The quality of the selected features will decrease especially on datasets with few instances.

• B.    Improving ensemble features selection

Two solutions are proposed to reduce overfitting problem and improve ensemble feature selection performance.

• a.    Multi Bagging technique

Overfitting is a serious problem when the library of models contains a huge number of models. As the number of models in the library increases, the chance to find model combinations that overfit increases as well.

Bagging technique can minimize this issue by creating multiple bags of models. Each bag contains a random sample of models which is less than the number of models in the library. Then inside each bag, we select models from that sample as shown in figure 2.

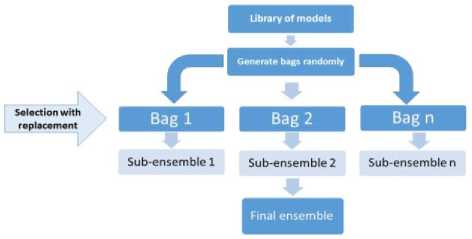
Fig.2. Ensemble selection algorithm

Below is a detailed description of Multi-bagging ensemble selection:

Algorithm 3: ENSEMBLE SELECTION WITH MULTI

BAGGING

STEP 1 : Ensemble initialization

• ■    The final ensemble weight is initialized at zero.

STEP 2 : Repeat for a fixed number of bags.

• ■    Generate a random bag of models

• ■    Apply the selection with replacement algorithm in order to select the best models from the generated bag.

• ■    The weight of the best models is incremented

STEP 3 : Return the weight of merging bags

• ■    The final weight is the merging weight of each bag.

• ■    The features whose absolute weight is the greatest are the best features.

• b.    Dropout technique

Dropout technique [12] is proposed to address the problem of overfitting in neural network. The idea behind this technique is to randomly drop units from neural network during the training phase. The units have the same probability to be dropped out from the network. By dropping a unit out, we are temporarily removing it from the network with all its incoming and outgoing connections as shown in figure.1

In this article, we proposed three versions of dropout. The first one is called Model dropout, the second is instances dropout and the third version is Combined dropout.

• a)    Model dropout

This technique has another way to evaluate ensemble’s performance by dropping out models from the ensemble randomly. This prevents models from the co-adaptation (correlation).

The following steps illustrate how Model dropout works:

Algorithm 2: MODEL DROPOUT

STEP 1: Weight initialization.

• ■    All models have the same initial weight equal ZERO.

STEP 2: Repeat until no increasing in ensemble performance or all models are examined.

• ■    Drop N models randomly from the ensemble.

• ■    Apply selection with replacement algorithm

STEP 3: Return The Ensemble weight.

• ■    The models are sorted by their weight. The best models are those whose weight is the highest.

• b)    Instance dropout

This method is a variation of dropout where instances are dropped out instead of models (features). At each iteration, an amount of instances is left out of the selection process to minimize the co-adaptation between instances as well, which helps to avoid overfitting problem.

• c)    Combined dropout

This version is a combination of the two versions Model dropout and instances dropout. This means that an amount of instances and features is dropped out at the same time.

• IV. Experimantal Results and Discussion

In this section, we conduct an extensive set of experiments to evaluate the performance of the proposed ensemble feature selection algorithms. We will first present the benchmark datasets. Then, we will describe the experimental setup. Finally, we will show and discuss the obtained results.

• A.    Data

We experiment with eight publicly available benchmarking datasets. All of the datasets can be downloaded from UCI machine learning repository [15].

Table 1 shows the statistics of the datasets used in our following experiments.

Table 1. Datasets and their characteristics

Dataset	Features	Instances	Distribution	classe
ds1.100	100	26,733	3% + / 97% -	2
credit card	24	30000	22% + / 78% -	2
ionosphere	34	351	64% + / 36% -	2
spambase	57	4601	39% + / 61% -	2
Musk	167	6598	15% + / 85% -	2
Sonar	59	208	47% + / 53% -	2
numerai	21	96320	50% + / 50% -	2
caravan	86	5822	6% + / 94% -	2

We carefully choose datasets to be different in terms of the number of instances and attributes to figure out the strengths and the weaknesses of the proposed methods.

• B.    Model libraries

Model libraries are generated using different classifiers and parameter settings. In our algorithm, each model is trained using just one feature. The library contains (the number of features multiplied by the number of classifiers) models.

The final subset of selected features is evaluated using a Random Forest with a grid search strategy for the hyper-parameters. The AUC score is computed using the out of bag (OOB) score of the random forest model.

• C.    Experiments

In this section, we conduct two sets of experiments to evaluate the performance of our proposed ensemble feature selection algorithms. We will first evaluate the ensemble selection with and without replacement technique. We will then demonstrate the applications of the proposed algorithms on eight benchmark datasets.

• •    In the first experiment, we compare feature selection with replacement against feature selection without replacement. This experiment is conducted to figure out the effectiveness of feature selection with replacement at reducing the problem of overfitting, because this algorithm allows features to be added to the ensemble multiple times. Moreover, the first experiment demonstrates that as the ensemble performance on the validation set increases, the corresponding performance on the test set does not always increase. This means that sometimes the ensemble selection overfits the validation set.

• •    The second experiment is concerned with evaluating the suggested algorithms which are useful in reducing the problem of overfitting and improving the ensemble selection performance as demonstrated by the benchmarking results. The algorithms at question here are: Without bagging, Multi bagging, Model dropout, instances dropout and Combined dropout.

• D.    Experiment 1: Ensemble feature selection.

In this experiment, we compare Selection with replacement algorithm to Selection without replacement algorithm described in the introduction section. Moreover, we show how the two algorithms behave on the validation and test set as shown in figure 3.

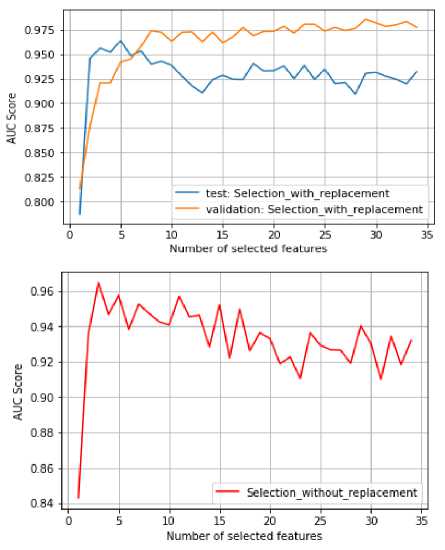
Fig.3. Selection with and without replacement using validation and test set

With models selection without replacement, the ensemble performance increases as the best models are added to the ensemble. Once the best models are added, the performance start declining because the best models in the library have been selected and there left just the models that are detrimental to the ensemble. This leads the ensemble to overfit. This behavior is shown through the red curve of the figure 3. As we can see after selecting the best 5 features, Ensemble selection without replacement starts adding the worst features to the ensemble, which is expressed by the drop in performance. This problem is reduced using models selection with replacement by allowing models to be selected multiple times as demonstrated by the orange curve.

The orange curve is the validation set performance and the blue one is the test set performance. They demonstrate that as the number of features in the library increases, the performance (in terms of AUC) of ensemble selection with replacement on the validation set drastically increases. However, the corresponding performance on the test set does not always increase. This clearly explains that the ensemble features selection sometimes overfits the validation set.

• E.     Experiment 2:  Ensemble feature selection

improvement.

In this experiment, we evaluate our proposed feature selection algorithms and the motives behind the chosen parameters of each algorithm.

• a.    Multi_bagging parameters

• a)    Number of bags

The number of bags used is 30. This choice is made after evaluating the algorithm with different numbers of bags as shown in the figure 4. We noticed that the more bags used, the better the performance is. In addition, Multi-bagging algorithm becomes more resistant to overfitting problem, because with more bags the best features have a high chance to be selected over the worst features.

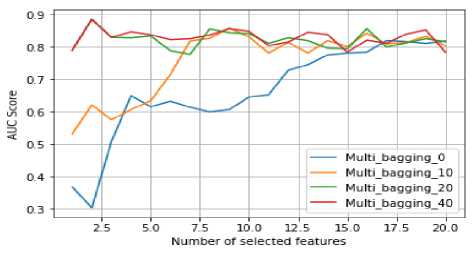
Fig.4. The effect of the number of bags parameter

• b)    Model portion

This parameter indicates the number of models in each bag. The choice of this parameter is related to the Number of bags parameter. We observed from the results conducted that when the number of bags is much higher, it is to choose a large ensemble, and vice versa. In our case, we set Model portion to be one third of the library.

• b.    Model dropOut parameters

• a) Portion of features dropped out

This parameter indicates the number of features to be out during the selection procedure at each iteration. This parameter depends on the number of models in the library. The more models in the library the more features should be dropped out from the ensemble.

• c.    Classifiers used to build library

The library of models is generated using decision tree classifier with different depths parameter (max_depth=2, max_depth=3, max_depth=4). Even if the library we generated is not that huge, our algorithms prove to be effective. To reach the best of our proposed algorithms, the library of models should be huge and diverse.

Table 2. The best parameters used for each dataset

Dataset	Instance dropped	Model dropped	Number of bags
ds1.100	0.4	0.5	30
credit card clients	0.2	0.6	30
ionosphere	0.1	0.3	30
spambase	0.5	0.3	30
Musk	0.4	0.2	30
Sonar	0.1	0.3	30
numerai	0.4	0.2	30
caravan	0.3	0.3	30

Several observations can be drown from the results of the second benchmark shown in Figure 3. First, we found that our Ensemble selection algorithm (Combined dropOut) outperforms our Multi bagging, Instances dropout and Model dropout Feature selection algorithms considerably in most of datasets especially datasets with high number of instances such as spambase, ds1.100, credit card client, caravan and Musk datasets. Whereas, Multi_bagging and Model_dropOut show their effectiveness on datasets with few number of instances as displayed in datasets sonar and ionosphere. This is totally logical because Combiend_dropOut algorithm drops out a portion of instances during the selection process. This reduces the number of instances of datasets. This problem does not appear in datasets with huge number of instances because even if a portion of instances is dropped out during the selection process, the datasets will still have enough instances. This verifies the efficacy of Compbiend_dropOut and its promising potential for large-scale data mining tasks.

• V. Conclusion

0.525 0.520 0.505 0.500

This paper proposed a new feature selection approach based on ensemble selection from the library of models, which is an effective learning method over the past several years. The ensemble feature selection algorithms are found to be effective in selecting the best subset among the whole space of features. The main contribution of this paper lies in the proposed ensemble selection framework. First, we created the library of models. Second, we used selection with replacement algorithm to select a well performing ensemble of models. To further improve the proposed feature selection algorithm and reduce the overfitting problem, we proposed two algorithms, the first uses the multi-bagging technique and the second uses the dropout technique. Experiments with eight benchmarks datasets show that our algorithms work well at selecting the best performing subsets of features.

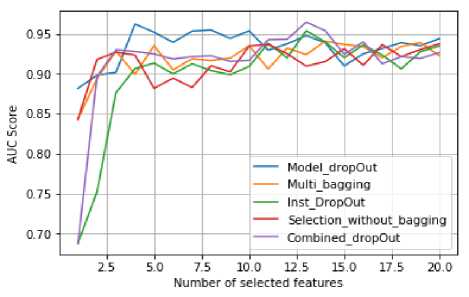
Fig.5. Results on ionosphere dataset using our proposed algorithms.X-axis is the auc-score of the final subset returned by each algorithm. y-axis is the size of the subset.

S 0515

< 0.510

ModeldropOut Multibagging InstDropOut Selection_without_bagging Co mb in ed_d ropOut --------------1-------------------------------1-------------------------------1------------------------

10.0    12.5    15.0    17.5

Number of selected features

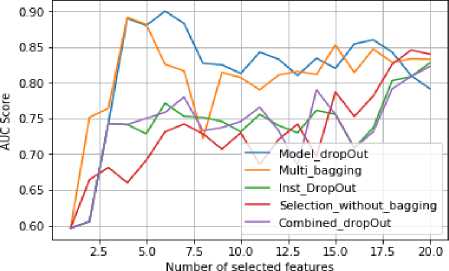
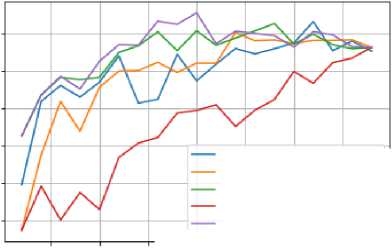
Fig.7. Benchmarking results on Sonar dataset.

Fig.6. Results on numerai dataset using our proposed algorithms.Model_dropOut, Multi_bagging, Inst_DropOut,Selection_without bagging, Combined_dropOut.

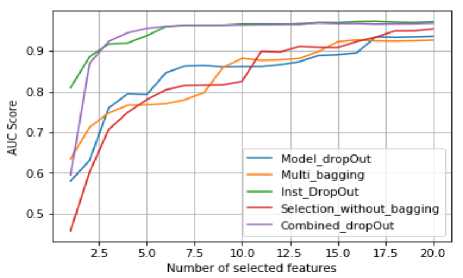
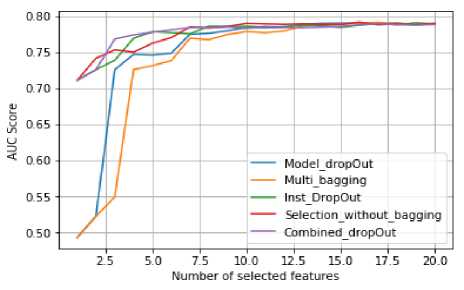
Fig.9. Results on credit card clients datasets.

Fig.8. Results on spambase datasets.

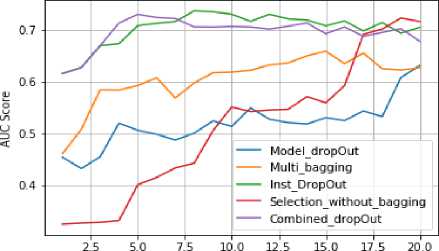
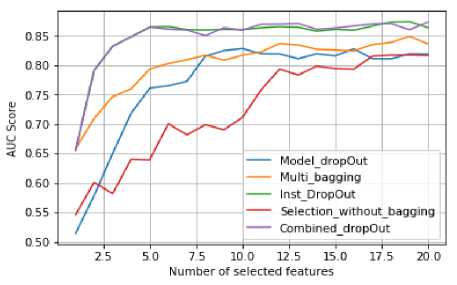
Fig.11. Results on ds1.100 datasets.

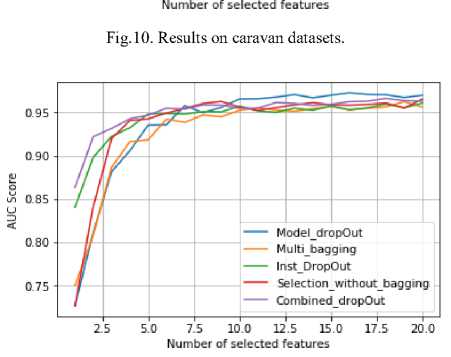
Fig.12. Results on Musk datasets.