Equations of motion of a single charge in vacuum

Equations of motion of a single charge in vacuum

Annotation

The motion of a single electric charge in a vacuum in the absence of any electromagnetic fields is considered. The system of Maxwell equations for this case is solved and it is shown that an electric charge with kinetic energy moves in a vacuum along a spiral path with a deceleration caused by the expenditure of energy on the magnetization reversal of the surrounding space.

Consider a single charge moving in a vacuum where there are no electromagnetic fields. Such a charge moves in a straight line at a constant speed. It is known that such a charge does not emit electromagnetic waves and does not consume energy for this process. However, a magnetic field is created around it, which is formed anew in each new position of the charge. This process requires energy consumption. Indeed, let us assume that the charge moves near a body made of magnetically soft material. Changes in the magnetic field in it cause magnetization reversal of the material, which consumes energy. This energy was expended by a moving charge. Therefore, the energy for restructuring the magnetic field is always consumed by the moving charge . Based on this premise, we consider a mathematical model of the motion of a single charge in a vacuum.

First of all, consider the system of Maxwell equations for such a charge. Following Eichenwald [1], the motion of a charge q. with a speed V. can be considered equivalent to an electric current

I = qv.                                 (1)

Therefore this movement is described in the same way as direct current -see appendix. This means that the charge cannot move strictly linearly, but moves in a spiral . Together with the charge, the flow of energy moves, equal in this case to the kinetic energy of the charge. This energy flow corresponds to the Lorentz force

F = 7                       (3)

where p, p are absolute magnetic permeability and resistance to charge movement. Its origin will be shown below.

This force acts on the charges in the body of the wire. In our case, the flow of energy moves with the charge, and the Lorentz force acts on this charge. The flow of energy is known to be equal to power. Therefore, the power of the charge movement

P = Sb,(4)

where b is the charge cross-sectional area. On the other hand, it is known that the power

P = FVr, where V is charge volume. From (3, 4, 5) we find:

P =(6) pb' '

or

f = ^ vV

(6а)

where p, p are absolute magnetic permeability of vacuum and electrical resistivity to charge movement. This resistance is caused by the fact that the charge spends energy on the reformation of the electric field. On the third hand, it is known that power

P = pl2.

From (1, 6, 7) we find:

^ = pw

Hence, p = "" Fv.                        (9)

q у vb                                  ' '

Finally, the power P is the power with which the kinetic energy of the charge is consumed, i.e.

P = mva,

where m, Cl are the mass and acceleration of the charge. From (5, 10, 3, 4,

6a, 9) we find:

_ FVv _ Spv _ Sp pb _ S b m mp mp p.V m V"

Thus, an electric charge with kinetic energy moves in a vacuum along a spiral path with a deceleration caused by the expenditure of energy on the magnetization reversal of the surrounding space.

Application. Mathematical model of direct current (summary according to [2])

In modeling, we will use the cylindrical coordinates г, ф, z in the SI system.

Maxwell's equations for a DC wire are:

where

rot(7) = 0 ,                                                         (а)

rot(H) — /—/o = 0 ,                                      (b)

div⁽J⁾ = 0 ,                                                         (с)

div(H) = 0 ,                                                    (d)

• the main current with a density Jo transmitted through the wire to the load, • additional currents with density J = (Jr,/ф,/z), • magnetic strengths H = (нг, Нф, Hz"). Equations (a-d) for cylindrical coordinates have the form: Ну . дНт + 1 ЭНф + dHz   0 r    dr r Эф    dz     ’ see (d) (1) 1 dHz ЭНф = j r Эф    dz Гт' see (b) (2) ЭНу _ dHz _ . dz dr =^ф' see (b) (3) Н»^2Н»_1_.Э* r + dr r Эф   Jz + Jo' see (b) (4) ]У | Э]У | 1 , Э)ф | d)z   0 r    dr r Эф    dz     , see (с) (5) l.dh.-Эф = 0 r Эф    dz     , see (a) (6) Э"Г-Э"Г = 0, dz dr see (a) (7) ]ф । d]ф  1 d]y   0 r    dr r Эф     . see (a) (8) To shorten the notation, we will use the following notation: co = cos( аф + xz), (10) si = sin( аф + xz), (11) where a, X are some constants. For these equations, there is a solution that has the following form:

Zr = Jr CO,(12)

Jp = jp si,(13)

Jz = Jz si,

Hr = hr co,(15)

И<р   кф si,

Hz = hz si, where j(r), h(r) are known functions of the r coordinate. At a given r, all currents and magnetic strengths are on helical lines. In fig. 1 shows three helical lines described by current functions (10, 11) with projections ]ф and Jz at r = const. These projections are determined by (13, 14), i.e. depend on the function si. In fig. 1 shows a thick line at a = 2,, / = 0.8, a middle line at a = 0.5,,/ = 0.8 and a thin line at a = 2, / = 1.6.

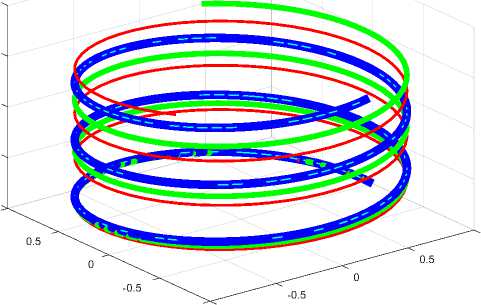
Fig. 1.

(TokPotok33.m)

-1        -1

The flux density of electromagnetic energy - the Poynting vector is determined in this case by the formula:

S = E x H.(18)

The currents correspond to the electric strengths of the same name, i.e.

E = p-J,(19

where p is the electrical resistivity. Combining (18, 19), we get:

S = pJ x H = ^J x B.(20)

The magnetic Lorentz force acting on all charges of the conductor in a unit volume - the volume density of the Lorentz force is

F = J x B.(21)

From (20, 21) we find:

F = nS/p.(22)

Consequently, in a direct current wire, the density of the Lorentz magnetic force is proportional to the Poynting vector .

So, a current with a density J creates a flow of energy with a density S that is identical to the Lorentz magnetic force with a density F. This Lorentz force acts on charges moving in a current J in a direction this current. Therefore, it can be argued that the Poynting vector creates an emf. in the conductor.

In cylindrical coordinates, the electromagnetic energy flux density (3) has three components S _r , ■ ф , S _z directed along the radius, along the circumference, along the axis, respectively:

■•Is 'rl                 /фН- (Jz + Jо)Нф1 ф • p(J X Н) • p\jzHr- JrHz + JoH .         (23) 'z!                [/гНф-/фНг + JтHoф\ where

Н _оф = кт .                                                (24)

So, streams of electromagnetic energy circulate in the wire . They are internal. They are generated by currents and magnetic strengths created by these currents. In turn, these flows act on currents as Lorentz forces. In this case, the total energy of these flows is partially spent on heat losses but mainly transferred to the load.

Longitudinal energy flow S _z . equal to the power P transmitted through the wire:

. P = S z ■         .                                        .         (25)

This power varies along the wire because part of the energy is spent on heat loss. With a known energy flux and geometric dimensions of the wire, the constants a, % can be found.

Thus, it is shown that there is such a solution of Maxwell's equations for a wire with direct current, which corresponds to the concept of

• •    the law of conservation of energy,

• •    helical path of direct current in the wire,

• •    transferring energy along and inside the wire,

• •    dependence of the helical trajectory density on the transmitted power.