Error Detection in a Multi-user Request System Using Enhanced CRC Algorithm

Published Online August 2014 in MECS

Errors in data cause a variety of problems and raises costs in several areas. The cost due to lack of data and availability of unreliable data are very serious. It is important to be able to detect these errors in other to proffer mitigation for the error related challenges. Detecting data errors in programs often takes as much, or more, of the analysis and programming efforts than the main logic. The earlier an error is detected, the cheaper it is to correct it. A common way of detecting error is rekey verifying selected data items, combined with programs that look for invalid data [3]. In a multi-user system, error detection can be much more tasking, such that re-key verifying alone may not be enough.

An error detection scheme is a crucial part of feedback error correction schemes such as ARQ (Automatic Repeat reQuest), which are required for attaining reliable communications over unreliable channels. The most important performance measure for an error detection scheme is its undetected error probability, which is the probability corresponding to the event such that an erroneous received word passes the detection test [11].

A multi-user request system is a system that allows multiple users on different computers or terminals to access a single system with one OS (Operating System)

on it. These systems are often quite complicated and must be able to properly manage the necessary tasks required by the different users connected to it. The users will typically be at terminals or computers that give them access to the system through a network, as well as other machines on the system such as printers. A multi-user system differs from a single-user system on a network in that each user is accessing the same program at different machines. In online query, web users can issue semantic query to the system which can be accessed by many other users [13].A multi-user system usually involves a large amount of information shared among its users. Multi-user operating systems and application software have been in use for decades and are still pervasive today. Those systems allow concurrent access by multiple users so as to facilitate effective sharing of computing resources [12].

The operating system on a computer is one of the most important programs used. It is typically responsible for managing memory and processing for other applications and programs being run, as well as recognizing and using hardware connected to the system, and properly handling user interaction and data requests. On a system using a multi-user operating system this can be even more important, since many people require the system to be functioning properly simultaneously. This type of system is often used on mainframes and similar machines, and if the system fails it can affect dozens or even hundreds of users connected to the system for services.

In a multi-user request system, for example, the system may need to handle numerous users attempting to use a single resource simultaneously. The system processes the requests and places the task in a queue that keeps them organized and allows each job to be carried out one at a time. Without a multi-user request system, the jobs or data management could become intermingled and the resulting information pages would be virtually incomprehensible and error prone. Nevertheless, in information theory with applications in computer science and telecommunication, error detection or error control are techniques that enable reliable delivery of digital data over unreliable communication channels. Many communication channels are subject to channel noise, and thus errors may be introduced during transmission from the source to a receiver. Error detection techniques allow detecting such errors, while error correction enables reconstruction of the original data [1].

• A.    Error

Science and engineering often involves measurements of different types. It is important to understand the nature and sources of errors, and know ways to detect and estimate them [8]. We must be familiar with the meaning of errors and with methods to compare data from various experiments as well as with theoretical model results. Good understanding of the meaning errors is needed in other to know how to detect them. Detecting data error could involve the use of theoretical models and performance measures can be done by checking the undetected error probability of the scheme [11].

The word “error” entails different meanings and usages relative to how it is conceptually applied. The concrete meaning of the Latin word "error" is "wandering" or "straying". Unlike an illusion, an error or a mistake can sometimes be dispelled through knowledge (knowing that one is looking at a mirage and not at real water does not make the mirage disappear). For example, a person who uses too much of an ingredient in a recipe and has a failed product can learn the right amount to use and avoid repeating the mistake. However, some errors can occur even when individuals have the required knowledge to perform a task correctly. Examples include forgetting to collect change after buying chocolate from a vending machine and forgetting the original document after making photocopies. Some errors occur when an individual is distracted by something else.

Technically, an error is the difference between a computed or measured value and a true or theoretically correct value. An error is the change or the mismatching which take place between the data unit sent by transmitter and the data unit received by the receiver e.g. 11101010 is sent by sender and 10101010 is received by receiver; the second digit from the left is altered from 1 to 0 on transmission.

• B.    Organization of the Paper

This paper presents review of literature on error detection and some error detection techniques in section II. It also performed an analytical findings based on the CRC error technique, its strength as well its weaknesses in section III. Based on the weakness in execution some enhancement was done on the algorithm which proved to be effective and showed higher and better rates of detecting error when implemented in section IV compared with the other technique in literature. Sections V, VI and VII presented the Summary, Conclusion and Recommendation respectively.

• II.    Error Detection

Regardless of the design of a system, there may still be errors, resulting in the change of one or more bits in a transmitted frame. When a code word is transmitted within the system, one or more number of transmitted bits of data will be reversed due to transmission impairments. Thus error will be introduced. It is possible to detect these errors if the received code word is not one of the valid code words. To detect the errors at the receiver, the valid code words should be separated by a distance of more than 1 [8]. Nevertheless, in error detection, whenever bits flow from one point to another, they are subject to unpredictable changes because of interference. This interference can change the shape of the signal. In a single-bit error, a 0 is changed to a 1 or a 1 to a 0. The term single-bit error means that only 1 bit of a given data unit (such as a byte, character, or packet) is changed from 1 to 0 or from 0 to 1. The term burst error means that 2 or more bits in the data unit have changed from 1 to 0 or from 0 to 1.

• A.    Error Redundancy Detection.

The concept of including extra information in the transmission of error detection is a good one. But instead of repeating the entire data stream, a shorter group of bits may be appended to the end of each unit. This technique is called redundancy [9] because the extra bits are redundant to the information; they are discarded as soon as the accuracy of the transmission has been determined.

In fig.1 the process of using redundant bits to check the accuracy of data unit is illustrated. In this fundamental concept, the data stream (11100000000101010) is generated and it passes through a device that analyzes it and adds on appropriately coded redundancy check value (111011101). The value is communicated using the appropriate channel to the receiver. In the receiver mode, the entire stream is put through a checking function. If the received bit stream passes the checking criteria, the data portion of the data unit is accepted but if the bit stream fails the checking criteria the data is rejected and the redundant bits are discarded.

Sender mode

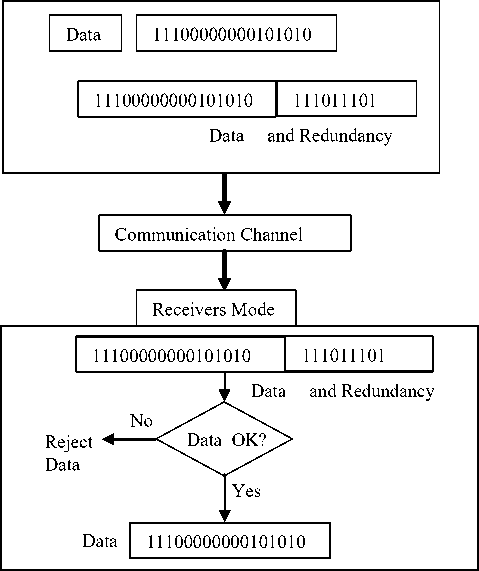
Fig. 1. Use of redundant bits to check the accuracy of a data unit. (Courtesy: [9] modified)

If the data stream passes the checking criteria we can infer that the data is not corrupted on transit and that the information is not tampered with or error-injected on transit along the communication channel used in moving the information from the sender to the receiver. We found out that the efficiency of this error detection technique depends largely on the checking function. If the message processing process are adequate and the checking function can handle checking process efficiently then the result expected could be dependable. But if the checking function is slow or the corrupting system can manipulate its operations then the system will not be reliable. However the actual challenge is on the volume of information for checking which shifts concern more in the direction of the efficiency of the checking process since the currently used checker have been said by Thamer [9] to be accurate. The checker may be simple or complex but it is not the simplicity or the complexity that determine the efficiency and efficacy of the checking process or its algorithm when large transmitted data is considered.

• B.    Simple Parity Check

The most common and least expensive mechanism for error detection is the parity check. Parity checking can be simple or two-dimensional as illustrated in fig.2.

In this technique, a redundant bit, called a parity bit, is added to every data unit so that the total number of bits in the unit (including the parity bit) becomes even (or odd).

Parity Checking

Simple

Two dimensional

Fig. 2. Parity Checking

• C.    Two Dimensional Parity Check

A better approach is the two dimensional parity checks In this method, a block of bits is organized in a table (rows and columns).

Accept Data

Transmission mode

Fig. 3. Two Dimensional Parity Checker (Courtesy [9])

First we calculate the parity bit for each data unit. Then we organize them as showing in fig. 3. We then calculate the parity bit for each column and create a new row of 8 bits. They are the parity bits for the whole block. The first parity bit in the fifth row is calculated based on all first bits; the second parity bit is calculated based on all second bits, and so on. We then attach the 8 parity bits to the original data and data and sent to the receiver. For example, suppose the following block is sent:

10101001 00111001 11011101 11100111 10101010

However, it is hit by a burst noise of length 8, and some bits are corrupted.

10101001 1000 1001 11011101 11100111 10101010

When the receiver check the parity bits, some of the bits do not follow the even-parity rule and the whole block is discarded (the non marching bits are shown in bold).

10101001 1 0 00 1001 11011101 11100111 10101010

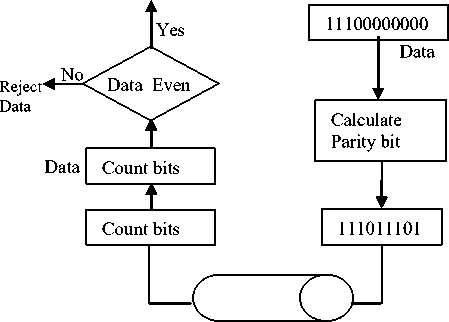
• D.    Parity Generator

  Assuming the number giving us is 11000011. Before transmitting we pass the data unit through a parity generator. The parity generator counts the bits and appends the parity bit to the end. The total number of bits is now an even number. The system now transmits the entire expanded unit across the network link. When it reaches its destination, the receiver puts all 8 bits through an even parity checking function. If the receiver sees

  11000011, it counts four is, an even number and the data unit passes. But, if instead of 11000011, the receiver sees 11001011 then when the parity checker counts the 1s it gets 5 an odd number. The receiver knows that an error has been introduced into the data somewhere and therefore rejects the whole unit. In fig. 4, it is clear that the data that have even 1s are assigned 0, making 0111001 to be 01110010 but the other data with odd 1s are assigned 1 to make the data even making 1100111 to be 11001111, 1011101 to be 10111011 and making 0101001 to be 01010011. Column parity is generated also to make the bits even up column-wise producing the last set of data 1100

1100111   1011101 0111001 0101001

1     0    0     1     1     1     1

The receiver treats the whole string as a unit and divides it by the same divisor that was used to find the CRC remainder. If the string arrives without error, the CRC checker yields a remainder of zero and the data unit passes. If the string has been changed in transit the division yields a non-zero remainder and the data unit does not pass.

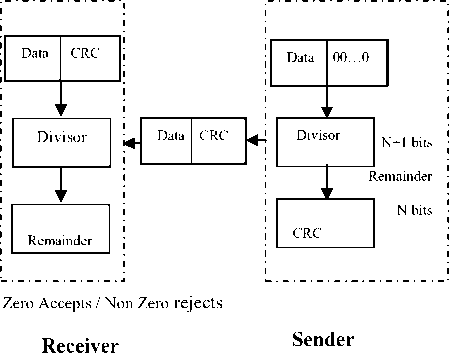
Fig. 5. Cyclic Redundancy Checker

Fig. 4. Data and Parity Bit Generation

• E.    Cyclic Redundancy Check (CRC)

Cyclic Redundancy check method is a powerful mechanism of error detection. Unlike the parity check which is based on addition, CRC is based on binary division. In CRC, instead of adding bits to achieve a desired parity, a sequence of redundant bits, called the CRC or the CRC remainder, is appended to the end of a data unit so that the resulting data unit becomes exactly divisible by a second predetermined binary number. At its destination the incoming data unit is divided by the same number. If at this step there is no remainder, the data unit is assumed to be intact and is therefore accepted. A remainder indicates that the data unit has been damaged in transit and therefore must be rejected. The redundancy bits used by CRC are derived by dividing the data unit by a predetermined divisor, the remainder is the CRC. A CRC must have two qualities. It must have exactly one less bit than the divisor, and appending it to the end of the data string must make the resulting bit sequence exactly divisible by the divisor.

• F.    CRC Generator and Checker

First, a string of n 0’s is appended to the data unit. The number n is less than the number of bits in the predetermined divisor, which are n + 1 bits.

Second, the newly formed data unit is divided by the divisor, using a process called binary division the remainder resulting from this division is the CRC.

Third, the CRC of n bits derived in step 2 replaces the appended Os at the end of the data unit. The data unit arrives at the receiver data first followed by the CRC.

• G.    Checksum Error Detection

Another method of error detection uses a process known as checksum to generate an error-detection character. The character results from summing all the bytes of a message together, discarding and carries over from the addition. Again, the process is repeated at the receiver and the two checksums are compared. A match between receiver checksum and transmitted checksum indicates good data. A mismatch indicates an error has occurred. This method, like CRC, is capable of detecting single or multiple errors in the message. The major advantage of checksum is that it is simple to implement in either hardware or software. The drawback to checksum is that, unless you use a fairly large checksum (16- or 32-bit instead of 8-bit), there are several data-bit patterns that could produce the same checksum result, thereby decreasing its effectiveness. It is possible that if enough errors occur in a message that a checksum could be produced that would be the same as a good message.

• H.    Check Sum Generator

In the sender, the check sum generator shown in fig.6 subdivides the data unit into equal segments of n bits.

These segments are added using ones complement arithmetic in such a way that the total is also n bits long. That total is then complemented and appended to the 1 and 0 the original data unit as redundancy bits called the check sum field. The extended data unit is transmitted across the network. So if the sum of data segment is T, the checksum will be T.

• I.    Checksum Checker

99.9% accurate. The cost is similar to the cost to key the

The receiver subdivides the data unit as above and adds all segments and complements the result. If the extended data unit is intact, the total value found by adding the data segments and the check sum field should be zero. If the result is not zero, the packet contains an error and the receiver rejects it.

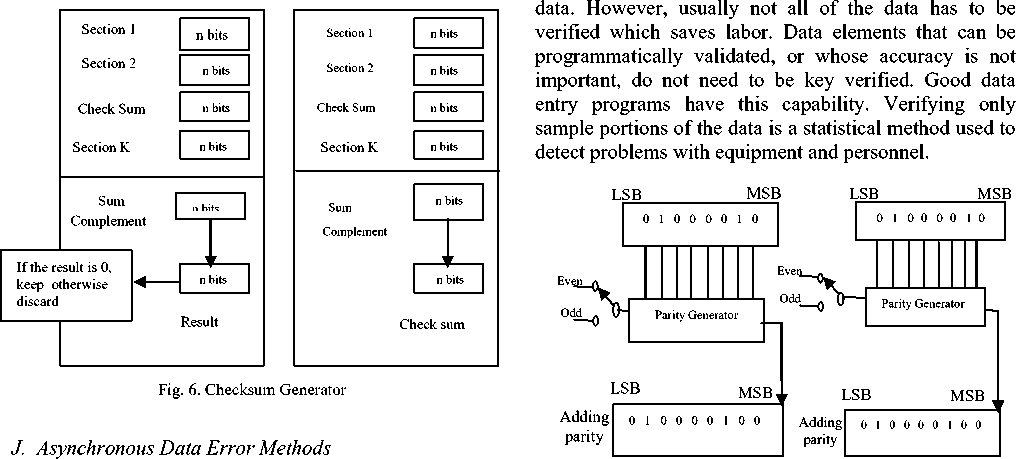
Fig. 7. Even Parity for ASCII B (a) Parity for Bad

Probably the most common and oldest method of error detection is the use of parity. While parity is used in both asynchronous and synchronous data streams, it seems to find greater use in low-speed asynchronous transmission application; however, its use is not exclusive to that.

• K.    Parity Error Detection

Parity works by adding an additional bit to each character word transmitted. The state of this bit is determined by a combination of factors, the first of which is the type of parity system employed. The two types are even and odd parity. The second factor is the number of logic 1 bits in the data character. In an even parity system, the parity bit is set to a low state if the number of logic 1s in the data word is even. If the count is odd, then the parity bit is set high. For an odd parity system, the state of the parity bit is reversed. For an odd count, the bit is set low, and for an even count, it is set high. To detect data errors, each character word that is sent has a parity bit computed for it and appended after the last bit of each character is sent as illustrated in Fig. 7. At the receiving site, parity bits are recalculated for each received character. The parity bits sent with each character are compared to the parity bits the receiver computes. If their states do not match, then an error has occurred. If the states do match, then the character may be error free.

• L.    m anual d etection m ethods

There are also two manual error detection methods. Proofreading (or sight verification) is the most common method. It is not especially accurate because the mind has a way of fooling our eyes. Nevertheless, it finds many errors. Surprisingly, continuous proofreading is not as fast as key entry. Some reject re-entry systems provide for selected proofreading while the rejects are being corrected. This can be a valuable feature. Re-key verify is the time proven method of manual error detection. Over decades of use it has been proven to be about

• III.    Analytical Findings

Data or database is said to be defective or error prone if there is any form of inconsistency in the content of data sent and the data stored in the database. Error or defect detection analysis reduces the time, resource, and cost required to rework, re-store and retransmit data within a multi-user database environment. Early data defect detection prevents data defect migration to archives or other repository of the data store. It also enhances reliability and maintenance of stored data in the database. Hence there is a continuous need to test data in the database and data that are backed up before they are archived [15]. In is not ideal to restore untested backup or to wait till there is need for database restore before data can be backed up.

When archiving backups there is a need to clearly label each backup volume. Special parameters are required to actually restore the database. The data however needed to be verified before they could be backed-up. This is done to check the status of the backup, to check if there are any bad (defective) blocks, and report whether the blocks are recoverable. The cyclic redundancy check (CRC) model and algorithm is one of the best check sum used in verifying defectiveness in the stored data [6].

In this paper we have looked at CRC but we still will analyze the CRC with the view of improving the model by adding module that checks transmitted data against stored data in the databases. This will require the extension of the CRC algorithm to achieve. The new algorithm can then be used in databases to compare the data stored and the data ready for archival so that data recovery when databases fail can be improved. This aids the correction of the challenge associated with having aspects of archives corrupted by electronic back-up processes.

• A.    Analysis of CRC System

CRC is very good on error detecting, however what have given error detection expert run for their effort is the way to discover and deploy the best generator polynomial that is adequate in handling increased volume of data both stored and transmitted across networks and servers.

In contemporary society, cloud computing, distributed computing and grid computing have added more impetus to the need to making sure that stored data in various locations and mirrors are not only consistent but error free. The users need to relax while they transmit the large volume of data from one point to another; and when their databases are archived for future reference. The need for generator polynomial is well known but getting the right polynomial is a different challenge. Different CRC standards have various generator polynomials.

The CRC polynomial generation is done by providing a new generator polynomial, improving on the algorithm and improving on the calculation implementation.

• B.    CRC-32 Design

In CRC system the Exclusive OR gate is at the point of receiving the message, the message is then moved from point 0 in register to point 31 in the register which is 32 points. In each of these registers corresponding bits are stored and used in processing the message to be able to check for error. The length of bit can enable double encoding which can be deployed in making attempt at recovering possible lost code. To develop a hardware circuit for computing the CRC checksum, we reduce the polynomial division process to its essentials. The process employs a shift register, which we denote by CRC. This is of length r (the degree of G ) bits, not as you might expect. When the subtractions ( exclusive or ’s) are done, it is not necessary to represent the high-order bit, because the high-order bits of G and the quantity it is being subtracted from are both 1.

• C.    CRC Algorithm Design

The enhanced CRC algorithm is described as:

Step 1: Start

Step 2: Initialize the CRC register to all 0-bits

Step 3. Hash message for operations.

Step 4: Get first/next message bit m.

Step 5: If the high-order bit of CRC is 1,

Step 6: Shift CRC and m together left 1 position, and XOR the result with the low-order r bits of G.

Otherwise,

Step 7: Just shift CRC and m left 1 position.

Step 8: If there are more message bits, go back to get the next one Go to Step 3.

It might seem that the subtraction should be done first, and then the shift. It would be done that way if the CRC register held the entire generator polynomials, which in bit form are bits. Instead, the CRC register holds only the low-order r bits of G , so the shift is done first, to align things properly.

Below is shown the contents of the CRC register for the generator G and the message M Expressed in binary, G = 1011 and M = 11100110.000 Initial CRC contents. High-order bit is 0, so just shift in first message bit. 001 High-order bit is 0, so just shift in second message bit, giving: 011 High-order bit is 0 again, so just shift in third message bit, giving: 111 High-order bit is 1, so shift and then XOR with 011, giving: 101 High-order bit is 1, so shift and then XOR with 011, giving:

001 High-order bit is 0, so just shift in fifth message bit, giving:

011 High-order bit is 0, so just shift in sixth message bit, giving:

111 High-order bit is 1, so shift and then XOR with 011, giving:

• 101 There are no more message bits, so this is the remainder. These steps can be implemented with the (simplified) circuit shown in Fig.8, which is known as a feedback shift register .

  

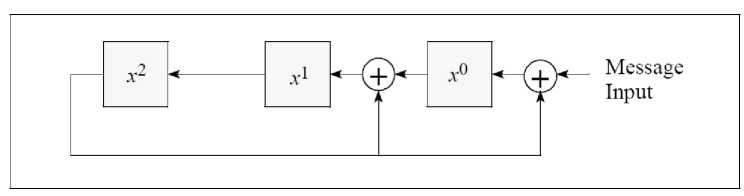
  Fig. 8. Polynomial division circuit for G = x ³ + x + 1.

  
  

The three boxes in the figure represent the three bits of the CRC register. When a message bit comes in, if the high-order bit (x2 box) is 0, simultaneously the message bit is shifted into the x0 box, the bit in x0 is shifted to x1, the bit in x1 is shifted to x2, and the bit in x2 is discarded. If the high-order bit of the CRC register is 1, then a 1 is present at the lower input of each of the two exclusive or gates. When a message bit comes in, the same shifting takes place but the three bits that wind up in the CRC register have been exclusive or’ed with binary 011. When all the message bits have been processed, the CRC holds M mod G. If the circuit of Fig. 8 were used for the CRC calculation, then after processing the message, r (in this case 3) 0-bits would have to be fed in. Then the CRC register would have the desired checksum, but, there is a way to avoid this step with a simple rearrangement of the circuit.

Instead of feeding the message in at the right end, feed it in at the left end, r steps away, as shown in Fig. 9. This has the effect of pre-multiplying the input message M by x^r . But pre-multiplying and post-multiplying are the same for polynomials. Therefore, as each message bit comes in, the CRC register contents are the remainder for the portion of the message processed, as if that portion had r 0-bits appended.

• D.    Challenges in the Designs

The behavior of checksum and cyclic redundancy check (CRC) algorithms have historically been studied under the assumption that the data fed to the algorithms was uniformly distributed. For instance, the work on Fletcher’s checksum [2] and the CRC-32 [10] shows that if one assumes random data drawn from a uniform distribution one can show a number of nice error detection properties for various checksums and CRCs.

Message Input

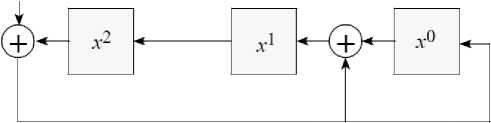
Fig. 9. CRC Design Circuit for Polynomial

But our observation on packet data is that in the real world, communications data is rarely random. Much of the data is character data, which has distinct skewing towards certain values (for instance, the character ‘e’ in English). The worst issue is that Unicode has made it possible to write complex programs that can convert data or even databases created and stored as text in English to say Chinese or even a Nigerian Language. This text and manipulations on them in stored data are rarely random. Even binary data has similarly non-random distribution of values, such as a propensity to contain zeros. In reports on experiments with running various checksums and CRCs over real data from UNIX file systems by Jonathan [4] show that the highly non-uniform distribution of values and the strong local correlation in real data causes extremely irregular distributions of checksum and CRC values. In some tests by Jonathan [4] less than 0.01% of the possible checksum values occurred over 15% of the time. This was supported, in part, by ARPA under Army Contract DABT63-91-K-0001 and in part, by the U.S. Department of Defense. We particularly examine the effects of this phenomenon when applied to the Internet checksum used for IP, TCP, and UDP [7] and compare it to two variations of Fletcher’s checksum. We also try to consider the overall effect on stored data and translatable databases as well as archival and decided to offer a design proposal called Extended-CRC (E-CRC).

• E.    E-CRC Design

In the E-CRC design the CRC is table driven. The table driven CRC routine uses a different technique than a loop driven CRC routine. The idea behind this design is that instead of calculating the CRC bit by bit, precomputed bytes are XORed to the data. The benefit of this improved proposal is that it is software driven instead of being hardware driven as the CRC-32. Since the hardware software loop is eliminated the design is expected to be faster than the loop driven solution. The drawback is that it may consume more program memory because of the size of the look-up table.

• F.    Design of Failure Rate Model

In a multi-user request system, data is usually distributed in such a way that data packets are often mixed with data from another packet. It is then important to compute checksum in pieces and then add the pieces to get the complete packet sum. Hence we think of the checksum of a packet broken into cells as being the sum of the individual checksums of each 48-byte cell. The usual requirement for a splice to pass the checksum is that the checksum of the splice add up to the checksum of the entire first packet contributing to the splice. Because the splice contains cells of the first and second packets, this requirement can also be expressed as a requirement that the checksum of the cells from the first packet not included in the splice must equal the checksum from the cells of the second packet that are included in the splice. If just one cell from the second packet is included in the splice, this requirement reduces to the requirement that the checksum of the cell from the second packet have the same sum as the cell it replaces. In multicell replacements, the sum of the mixes of cells must be equal.

Given random data, E-CRC should uniformly scatter the checksum values over the entire checksum space. Obviously a checksum algorithm that does not uniformly distribute checksum values (i.e., has hotspots) will be more likely to have multiple cells with the same checksum. We derived this view from examine existing theorem in [5] and [4]. The theorem further proves that, over uniformly distributed data, the checksum algorithm gives a uniform distribution of checksum values. Thus, any hotspots in the distribution of checksum values are due to non-uniformity of the data in a multi-user system, and are not inherent in the checksum algorithm.

Although for uniformly distributed data values the probability distribution of the checksum is uniform independent of the length of the block of data, this is not true for nonuniform data. In that case, the expected probability distribution of the checksum may be computed by

P k [ i ] = Σ (P k-1 [ j ]P i [ i-j ]) (1)

where P _k [ i ] is the probability that the checksum over a block of length k ( is equal to i ).

We can ”Predict k = 2” shows the expected distribution of checksums over blocks 2 cells long, given the checksum distribution over one cell given by k = 1. So, if the non-uniformity is uniform – that is, that every cell of data is drawn from the same probability distribution, and that the sum is the sum of independent samples – then we would expect the distribution of the sums to conform closely to the line in our graphs. The predicted value for k = 2 is already close to uniform for all but the 20 most common values, even though k = 1 is decidedly non-uniform. It also show that, regardless of the original distribution, the distribution should get more uniform as k increases. However, our measurements show that the non-uniformity extends to larger chunks than single words or cells, and that the checksum of one cell is correlated with the checksums of the neighboring cells. The data does get more uniform but nowhere as quickly as it should if the cells were roughly independent. We believe the samples should be somewhat representative even of non-contiguous blocks. Given the non-uniform distribution, what, then, is the expected failure rate of the IP/TCP checksum in detecting splices for a given distribution, P, of checksum values when data is transmitted from user to a database store. As discussed above, it is simply the probability that the checksum over the cells missing from the first packet is equal to the checksum over the cells present from the second packet. For a given probability distribution P this probability is

P(failure) = Σ P[ i ]² (2)

The models (eq 1 and eq 2) can be used to compute the probability of the checksum match for substitution of length k cells in the implementation of the system in this paper.

• IV.    Implementation and Result

The E-CRC is implemented using two different programming languages. The programming language for the development of the system is wxDev C++ and Assembly. These are selected because of its advantage in the development of System programs.

The program has an executable which runs on the console. The system can be executed on the windows from the command line by using the exe name used in debugging the program. The main page of the system produced input screen that allow the user to know when the system executes and produces the result.

• A. Result Profiling

The program was executed and profiled and data generated from the profiling is displayed as shown in table 1. The table 1 shows how the probability changes when we restrict the comparisons to only look at local data. The first column displays the probability of taking two blocks of data, each k cells long from anywhere in the entire file system and finding that their IP checksums were congruent to each other. The second column shows the same probability if we limit the search to be within 2 packets length (512 bytes).

Table 1. Probability (as %) of checksum match for substitution of length k cells

K	Globally	Locally Congruent	Excluding Identical
1	0.02126770	1.58305972	0.20704272
2	0.01494399	1.30267681	0.17226800
3	0.01348366	1.21236431	0.16614066
4	0.01416288	1.15970577	0.16316988

The third column shows how the probability decreases when we exclude checksum matches for a pair of blocks that contained identical data as such a substitution would not result in any data corruption. It is plotted for clarity in figure

In table 2 , the result show data on reduction of the checksum failure rates by the methods. The data for the other methods where gotten from literature while we presented them with our result. The data showed higher and better rates of detecting error when compared with the other technique in literature. The result of the checksum also show a remarkable improvement when we look at the original CRC checksum from where we extended the model.

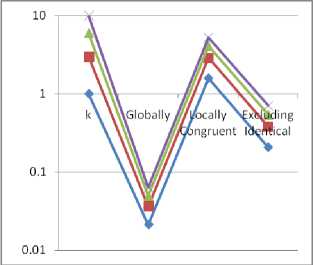
Fig 10. Plot of Probability (as %) of checksum match for substitution of length

Table 2. Table showing the Checksum result data in relation to E-CRC

Error Detection Method	Data Values
	Misses	Splices
F255	0.0044358811	138441
CRC	0.0021999117	316
TCP	0.1703438788	5316323
Extended-CRC	0.001002156	295

The data in the result table was plotted in an excel chart and the plotted chart is shown in fig.10. The interpretation from the figure show that the Extended-CRC developed in this thesis made a remarkable improvement compared to the original CRC result from literature.

The chart indicated that finding out the point of mismatch was faster in the Extended-CRC than the other methods covered in literature. The slowest showed the simple TCP and the Fletcher. The Fletcher however how a remarkable improvement from the TCP and the E-CRC show even further improvement from the already good CRC method.

• V.    Summary

This paper focused on error detection scheme that checks and detects error in Multi–user request system. Error and error related issues have been a challenge in the development and reliable usage of data in computing systems and application especially in distributed databases. The ability to detect minor error in a system enhances system reliability. This is particularly so when the data is used, transmitted and archived and may be retrieved for future usage. Users need to be certain that alteration of any kind does not occur when that data is moved. This process support developers and end – users to recognize possible challenges so that they can be resolved or fixed during development and even when the system have been put to use.

The approach considered in this paper improves on a Cyclic Redundancy Check (CRC) detection algorithms for the detection of error that may possible occur in data transmission by polynomial selection in computation and on stored, backed – up and archived data in the system. The plot in fig. 11 shows the result of the enhancement.

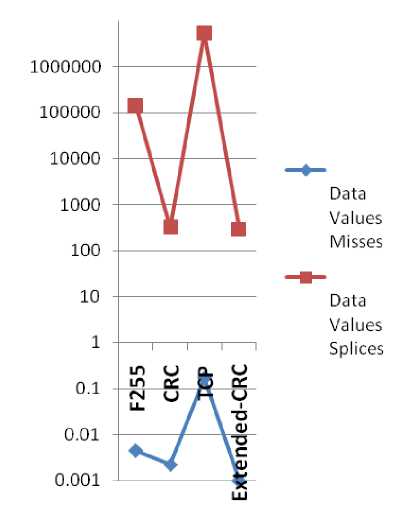
Fig. 11. A plot of the result of Enhanced-CRC

In a multi-user request system, the system must be able to handle the various needs and requests of all of the users effectively efficiently. In a multi-user request system, for example, the system may need to handle numerous users attempting to use a single resource simultaneously. The system processes the requests and places the task in a queue that keeps them organized and allows each job to be carried out one at a time. Without a multi-user request system, the jobs or data management could become intermingled and the resulting information pages would be virtually incomprehensible and error prone.

• VI.    Conclusion

In the paper we have implemented error detection in a Multi-Users Request System, which will serve as a framework for other error detection schemes. We have studied other schemes and designed an error checker for checking of error in system. We have also developed an error detections system for Multi-User Request Systems – E-CRC checker. The designed system in the paper has equally been implemented for detecting errors using checksum and improved CRC algorithm. In all, this paper has investigated a theoretical possibility of developing an error checking model which can be deployed in providing multi-user error checks. It also has made analysis of the present error checking systems and models that are used to be able to evaluate their strength and pitfalls in realizing the said objective within a stored data or database environment.

• VII.    Recommendation

Acknowledgment

The authors wish to thank Justina Udoh and Mercy Eke for typing the paper and encouraging us in writing the paper respectively. We appreciate the support of Oyol Computer Consult, Inc Choba, PHC Nigeria, (Java House) for the use of their research facilities in completing this work.