Еще один способ нахождения частных решений уравнений математической физики

DOI:

Нелинейные дифференциальные уравнения в частных производных (нелинейные уравнения математической физики) часто встречаются в различных областях математики, физики, механики, химии, биологии и в многочисленных приложениях [12]. Общее решение нелинейных уравнений математической физики удается получить только в исключительных случаях. Поэтому обычно приходится ограничиваться поиском и анализом частных решений, которые принято называть точными решениями [7; 11].

Точные решения дифференциальных уравнений математической физики всегда играли и продолжают играть важнейшую роль в формировании правильного понимания качественных особенностей многих явлений и процессов в различных областях науки и техники [12]. Можно сказать, что невозможность решить эти уравнения аналитически является препятствием для дальнейшего изучения многих физических явлений и применения их на практике. Допускающие точные решения модельные уравнения и задачи служат основой для разработки новых численных, асимптотических и приближенных методов, которые, в свою очередь, позволяют исследовать уже более сложные задачи, не имеющие точного аналитического решения.

Существуют различные приемы для поиска точных решений уравнений математической физики, например, метод дифференциальных связей [11]. В данной работе мы развиваем идеи наших предыдущих работ [1; 4; 5] и предлагаем новый метод нахождения частных решений систем дифференциальных уравнений, сводящийся к нахождению дополнительных уравнений связи и преобразованию этих систем в переопределенные системы неявных уравнений. Показывается, как, решая эти переопределенные системы неявных уравнений, можно находить, в том числе, и аналитические решения исходной системы дифференциальных уравнений или решать задачу Коши.

Рассмотрим переопределенную систему из p + n дифференциальных уравнений в частных производных первого порядка относительно неизвестных S _ν ( x ), ν = 1 ... p , x = ( x ₁, ... x_m )

H k

' S , S v , x ( o x

\

= 0 , v = 1... p , k = 1... ( p + n ) .

Продифференцируем выражения (1) N ₁ – 1 раз по переменной x ₁, N ₂ – 1 раз по переменной x ₂, … N_m – 1 раз по переменной x_m . В результате получим систему неявных уравнений вида

P a ( Q e , X ) =

d⁽ i ⁺-⁺ i m ) d x}..Sx m

( PS

Hk "57 , Sv , x ( o x

= 0 , v = 1... p , k = 1... ( p + n )

относительно неизвестных вида

Q β

d ⁽ j ¹¹ j m ) S

————, v = 1... p .

Ns = p •( N1 +1)( N2 +1)...(Nm +1).(7)

Из (2)–(5) видно, что реально некоторые высшие производные (3) не входят в выражения (2), то есть на самом деле от некоторых неизвестных Qβ выражения Pα не зависят. Выберем такие N1, ... Nm, чтобы выполнялось неравенство NS < NH (см.: (6)–(7)), то есть p • (N1 +1)(N2 +1)...(Nm +1) < (p + n)N1 N2...Nm или

/

к

/

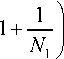
к

1+—

N 2

(     1 1

1+|< к N m )

(1+n 1

.

к p )

или

или

Рассмотрим частный случай N = N ₁ = N ₂ = ... = N_m . Тогда условие (8) означает, что

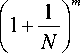
1+ n

p

(' n | ^— , I 1 ■ I - 1

к p )

m

N >  mp и N H = ( p + n ) N m > ( p + n ) | —p I .

В случае переопределенных уравнений Навье – Стокса, полученных авторами в работах [1; 4; 5], имеем m = 4, p ~ 10, n = 1, значит, из (9) N _min = mp / n » 40 и N_{H min} = ( p + n ) ( mp / n ) ^m » 10⁷.

Рассмотрим матрицу [2]

^А ав =

⁽ Q )

a = 1... N„ в = 1... N ,.

HS

Разберем расширенную переопределенную систему неявных уравнений вида

P a ( Q _P . x ) =

H k ^ ’ ^ ’ X к O X

= 0 , v = 1... p , k = 1... ( p + n )

относительно неизвестных вида

Q β

d^{( j} 1 ¹¹ j — ) ^

j 1 = 0... ( N 1 + 1 ) , j ₂ = 0... ( N 2 + 1 ) , _ j — = 0... ( N — +1 ) .                       (14)

Система уравнений (11) (с индексами из (13)) включает в себя систему уравнений (2). Неизвестных (12) (с индексами из (14)) несколько больше неизвестных (3). Докажем следующее утверждение.

Утверждение. Любая система из p дифференциальных уравнений в частных производных первого порядка, переопределенная любыми n дифференциальными уравнениями первого порядка (1) и редуцированная изложенным выше методом, переопределенная расширенная система неявных уравнений вида (11) от неизвестных вида (12) имеют одинаковое множество решений, если ранг матрицы (10) (на каждом решении этой расширенной системы неявных уравнений) равен количеству неизвестных Q_β, реально присутствующих в уравнениях (2).

Подсчет показывает, что это число не более

N™¹ <  N_H

SH

p

( P + n )

m i+z—I Z N J.

Поскольку мы допускаем, что ранг матрицы (10) равен N_S ^real , значит, существует N_S ^real независимых уравнений из системы (2) от такого же числа неизвестных [6; 13]. Обозначим их как

^P a. ( Q e . , X ) = ⁰, l = 1- N Se ¹¹ .

Здесь a - a kk1, i1. ,../У В, - в Vv1, j,... jl У Продифференцируем уравнения (16) по перемен-l ,1, m , l , 1, m ной x , 1 < 5 < m. Имеем

s

Nr a P _ai ^{Q Z} d Q e * * d x

^{d P}a ( Q _P1 , X ) a x₅

С другой стороны, из определения уравнений (11) следует, что p          NT dPa. Q dP (Qe , x) _0 ! Nre«l

P ⁽ Q e. , ^x P^ d q^ ^Q e * . ⁺ d x - ^{l -} 1... N S ,                    ⁽¹⁸⁾

Вычтем почленно из выражений (18) выражения (17). Тогда

N_S real

Z

i * - 1

^{5 P} a l ^d Q e. .

^Q l *

V

d Q_B ^β l ^*

- 0 l - 1... N™¹

, S

В силу нашего предположения относительно независимости уравнений (16) из выражений (19) следует [2]

(

Q el

V

d Qb I             ⁵ Q_B

-rrr - 0 или Q - -I^е- , l - 1... N_?l . a x_s )             ^el    a x_s

Таким образом, мы доказали, что для каждой переменной xs, 1 £ s £ m выполняется соотношение (20). Отсюда, учитывая, что по определению Qβ(ν, 0,...0) = Sν (x), ν = 1 ... p, следует dQ„, -       в(v, j1 -1,... jm )

'^в ( ^V , ^j 1 ,... ^j m ) ^—          d X

d ^j1Q_R(       i          d^{( j 1+ j 2} ) Q_{r( aa}

В ( ^{v ,0},... j m ) _{-    -}               ^e ( ^{v ,0,}0... j m )

a x j     ”...”      a xjex 2 2

₉ ( ^{j 1 +} ... + ^j m )Q                  ( j 1 + ... + j m )

Q e ( v ,0,...0 ) _- d S v

d x ,^j1 .. . d x m m         d x j .. . d x m m

В итоге мы показали, что функции S _ν ( x ), ν = 1 ... p являются решением (1), а величины (3) являются соответствующими частными производными этого решения (21).

Утверждение предлагает некоторое достаточное условие для существования сразу аналитического решения у переопределенных систем дифференциальных уравнений.

Это утверждение описывает некоторый прием для получения частных решений систем дифференциальных уравнений. А именно нужно выбрать уравнения связи таким образом, чтобы имело «хорошее» решение некоторая переопределенная система неявных уравнений, из которой находится частное решение.

Из формулы (8) следует, что

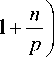
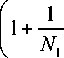
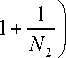
i A i i i

1 +--> 1 +---1---+ ... +-- .

NN N

< N m J ^N 1 N 2 N m

Следовательно, из (22) следует n11    1

— >--1---+ ... +--

p N 1   N 2      N m

В частности, из (23) следует

N l >  ^P , 1 <  l <  m . n

Тогда, используя известное соотношение между средним геометрическим, гармоническим и (23), мы имеем оценку для минимального количества редуцированных уравнений:

/

A m

^N H = ( P ⁺ n ) ^N 1 ^N 2 ... ^N m ^ ( P ⁺ n )

m

±+X+...+X I N 1   N 2      N m J

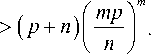
Как было показано выше (9), она реализуется при N = N 1 = N ₂ = ... = N m » mp / n . Если использовать выражения из (15) вместо (7), то мы получим такие же результаты (25).

Рассмотрим для примера следующую переопределенную систему ОДУ (осциллятор) [8; 9]:

ui = - v,(26)

■v = u,(27)

u + v = cos( t) + sin( t).(28)

Уравнения (26)–(28) имеют одно общее гармоническое решение u = cos(t), v = sin(t).(29)

Покажем, что оно в данной постановке задачи единственное. Здесь p = 2, n = 1, m = 1. Из формулы (24) следует, что N 1 > p / n = 2, то есть N 1 >  3. Продифференцируем уравнения (26)-(28) по переменной t N ₁ – 1 = 2 раза. Тогда

u = - v,

..

v = u ,

u + v = cos( t ) - sin( t ) ,

...

u = - v,

...

v = u ,

U + v = - cos( t ) - sin( t ) .

Мы имеем переопределенную линейную систему из 9 неявных уравнений (26)–(28) и (30)–

• (35)    и 8 неизвестных u , v , u , v , U, v , u и v . Матрица (10) имеет вид:

  	f 0	1	1	0	0	0	0	0 ^
  	- 1	0	0	1	0	0	0	0
  	1	1	0	0	0	0	0	0
  	0	0	0	1	1	0	0	0
  А ав =	0	0	- 1	0	0	1	0	0	(36)
  	0	0	1	1	0	0	0	0
  	0	0	0	0	0	1	1	0	.
  	0	0	0	0	- 1	0	0	1
  	1 0	0	0	0	1	1	0	0 V

Определитель матрицы, составленной из первых 8 строк и столбцов матрицы (36), отличен от нуля. Следовательно, ее ранг равен 8, то есть количеству переменных в системе (26)–(28) и (30)–(35) [2]. Дополним систему (26)–(28) и (30)–(35) до расширенной. Продифференцируем уравнения (33)–(35) по переменной t. Тогда u14) =

- v ,

v ' )

...

= u ,

u + V = - cos( t ) + sin( t ).

Система неявных линейных уравнений (26)–(28), (30)–(35) и (37)–(39) имеет только одно общее решение u = v = -u' = -v' = u(4) = cos(t), v = -u = -v = u' = v(4 = sin(t).              (40)

Следовательно, согласно нашему утверждению это решение (40) является решением переопределенной системы ОДУ (26)–(28), и других решений эта система не имеет. Соотношение (28) выделяет из системы (26)–(27) только одно решение (29). Интерес представляет некоторое обобщение этого результата, а именно если к системе (26)–(28) добавить произвольную внешнюю силу, а также заменить в уравнении связи (28) правую часть на произвольную функцию от времени (взятую, например, из измерений в эксперименте), то аналогичными рассуждениями получим, что решение новой системы уравнений будет находиться из линейной системы уравнений (26)–(28), (30)–(35) и (37)–(39), но с другой правой частью (в виде конкретной формулы). Причем если это решение не существует, то не существует решение и исходной обобщенной системы. А если существует, то оно единственно [2].

В среде MATHCAD авторами были исследованы и другие модельные примеры в двухмерном случае, в том числе и из работы авторов [4]. К сожалению, возможности среды MATHCAD ограничены размером оперативной памяти ЭВМ. Удается только промоделировать системы порядка ста уравнений, которые, естественно, мы не можем представить в данной работе в явном виде, хотя сам алгоритм получения решений переопределенных систем УрЧП, как видится авторам, довольно простой. Отдельная программа символьными операциями создает систему неяв- ных уравнений, а другая стандартными численными методами эту систему решает, используя результаты предыдущей программы как входные данные. Авторам представляется, что данная задача вызовет интерес для творчества у профессиональных программистов-математиков.

Предлагаемый в данной статье прием разработан и применим к любым системам дифференциальных уравнений в частных производных. Требуется только существование независимого переопределения, с помощью которого производится редукция исходной системы дифференциальных уравнений до переопределенной системы неявных уравнений. Если это будет сделано для любого определенного достаточно гладкого решения (например, выделенного с помощью задачи Коши), то мы можем найти аналитическое решение исходной системы дифференциальных уравнений в предположении его достаточной гладкости. В работах авторов [1; 4; 5] это переопределение пока только предлагается, в частности, для уравнений гидродинамики. Трудность заключается в том, что количество редуцированных неявных уравнений быстро растет с увеличением числа переменных в исходной системе дифференциальных уравнений (см.: (25)). То есть, чтобы их выписать и решить, необходимо произвести большое количество символьных операций. Для этого существуют специальные программы (MATHEMATICA, MATHCAD и др.) и среды, например, Лисп.

Во втором разделе статьи дана оценка количеству редуцированных неявных уравнений для некоторых переопределенных систем дифференциальных уравнений математической физики, полученных авторами в более ранних работах [1; 4; 5]. Мы видим, что это число может быть просто огромным. Одним из выходов может стать следующее: нужно стремиться получить как можно больше уравнений связи, чтобы как можно меньше было отношение mp / n (см.: (25)).

Следует отметить, что в работах авторов [1; 4; 5] производилось только преобразование от систем дифференциальных уравнений по объему к системам дифференциальных уравнений на поверхности. В форме гипотезы очевидным образом показывалась возможность дальнейшего сокращения размерности вплоть до полного решения задачи Коши или аналитического решения. Однако никаких условий, при которых обратно из огромного множества решений системы обыкновенных неявных уравнений выделялось именно нужное решение, удовлетворяющее исходной системе УрЧП, не приводилось. В данной работе показывается, какого именно числа систему редуцированных неявных уравнений нужно строить и решать и какое условие на определитель должно при этом выполняться. То есть все, что нужно для решения этой задачи на ЭВМ. Для удобства в предыдущих работах количество уравнений связи единица, в данной работе это число неограниченно.

Переопределенные системы уравнений, рассматриваемые в статье, использовались в теоретической физике и изучались и ранее, в частности, Картаном [10]. Может показаться, что предлагаемый в статье метод есть частный случай метода дифференциальных связей [11], являющийся обобщением метода теории групп. Однако сходство заключается только в наличии переопределен-ности и некоторой аналогии преобразований уравнений связи. В методе дифференциальных связей все равно необходимо решать дифференциальные уравнения определенного вида, тогда как в предлагаемом методе все сводится к решению систем обыкновенных неявных уравнений.

С помощью данного метода можно просто производить редукцию переопределенных систем дифференциальных уравнений, убирая производные у неизвестных функций по одной или нескольким переменным, но увеличивая их гладкость.