Естественные расширения кусочно-монотонных эндоморфизмов

В статье дается способ построения естественных расширений эндоморфизмов, заданных кусочно-монотонными функциями, в частности, /С-авто-морфизмов.

Пусть (М, F, р) — пространство Лебега [1], то есть пространство с вероятностной мерой, изоморфное отрезку [0, 1] с мерой Лебега. Таким пространством является, например, пространство М = [0, 1) х [0, 1) с мерой Лебега. В дальнейшем М обозначает именно это пространство.

Автоморфизмом пространства М называется взаимно однозначное сохраняющее меру преобразование этого пространства, обратное к которому также измеримо.

Эндоморфизмом называется измеримое не взаимно однозначное преобразование пространства М.

Автоморфизм Т пространства М называется К-автоморфизмом (автоморфизмом Колмогорова), если существует cr-подалгебра F_o С F такая, что выполняются -                     ⁰⁰

условия: 1) T^-kFo С F_o, 2) П T^-uFq = R (Я — тривиальная ст-подалгебра, содер- п=0

/ ОО        \ жащая только множества меры 0 и 1), 3) ст и TnFoj = F, то есть сг-подалгебра, порожденная образами множеств из Fo, совпадает с F.

Хорошо известно «преобразование пекаря» пространства М, определяемое формулой

Т(т,у) = |

(2т, jy), 0 ^ ж < j, 0 <  у < 1;

• (2ж - 1, У + |), | ^ ж < 1, 0 ^ у < 1.

Оно является А-автоморфизмом.

В дальнейшем мы будем рассматривать различные обобщения этого преобразования, в результате получая не только Д-автоморфизмы.

кт, ^ , 0 ^ ж < £, 0 <  у < 1, кт — 1, ^у + j), | < ж < ^, 0 ^ у < 1,                ^

кт - (к - 1), ку + Ь1) , у ^ ж < 1, 0 ^ t/ < 1.

При  этом  множество [^, |) х [0, 1) отображается на  множество

[О, 1) х [^, |) , г = 1, к. cr-подалгебра Fo = {В = А х [0, 1), Аб F[o, i)}, ^[о, i) - лебеговская cr-алгебра отрезка [0, 1). Т гВ = By = Ai х [0, 1), Ay е F[0, i). Ai = |A U (| + ^А) U ... U (^ + |А). Поэтому By Е Fo, то есть T^Fo С Fo.

Рассмотрим разбиение £ пространства М, элементами которого являются ж х [0, 1), х Е [0, 1). Это измеримое разбиение, соответствующее cr-подалгебре F_o. Измеримость разбиения £ следует из того, что это есть разбиение на прообразы точек для измеримой функции /(ж, у) = х. Так как разбиение С инвариантно относительно Т, то есть T^-1q ^ ^ (здесь неравенство означает, что элементы разбиения Т^-\ состоят из объединений целых элементов разбиения С). Поэтому существует фактор-эндоморфизм T_s на фактор-пространстве M/q. Мj<; есть пространство, точками которого являются элементы разбиения то есть множества х х [0, 1). Отображение Щ : М —> М/<;, при котором множество х х [0, 1) С М отображается в точку Н^хх [0, 1)) Е Мfq, называется естественным гомоморфизмом пространств М в M/q. При этом точку H_s(x х [0, 1)) можно отождествить с точкой х Е [0, 1), a M/q — с отрезком [0, 1). Из (1) следует, что при указанном отождествлении T_sx = кх (modi). Известно, что это точный эндоморфизм [2], что равносильно

П T~ⁿF₀ л = R, и поэтому П T~ⁿF₀ = R. п=0 ¹ ’ ' ' п=0

Итак, первые два свойства /Т-автоморфизма выполняются. Теперь заметим, что F_o U TF₀ содержит множества вида А х [^, £), г = 1, к и А х [0, 1), А Е F^ ц; F_o U TF₀ U T²F₀ содержит кроме указанных множеств множества А х [^,^)> г = 1, к², А Е F[₀,i) и т. д. Таким образом, мы можем аппроксимировать каждый прямоугольник, а следовательно, каждое множество из F множествами из FoUTF_oU.. .UT”F₀. Поэтому выполняется третье условие, и Т есть К-автоморфизм.

Известно [2], что для всякого эндоморфизма Ту пространства Лебега существует единственный автоморфизм Т, называемый естественным расширением эндоморфизма Ti, такой, что для него существует инвариантное разбиение £ (Т^-1 ^ ) и такой, что Ту изоморфен T_s (теорема Рохлина).

Таким образом, К-автоморфизм Т, построенный в предыдущем примере, есть естественное расширение эндоморфизма Тух = A;T(mod 1).

Аналогично можно рассмотреть отображения:

1. Жу^1

(2ж, ^у), 0 ^ я < |, 0 <  у < 1, 2(1 - х\ ^у + |, | ^ ж < 1, 0 ^ у < 1.

Это тоже А-автоморфизм с F_o = {В = Ах [0, 1)}, Т ¹F₀ = {Bi = Ay х [0, 1)}, f 2з? О ос ~

Ai = jA U (1 — ^Ау Tsx = < -,’ _ Л 1 2    1 , ^-«треугольное» отображе ние — точный эндоморфизм.

• 2.    Пусть ту^т^^т^ — действительные числа, большие единицы, такие, что А. +

1 = 1.

Г2 ГЗ

Т(т,г/) = <

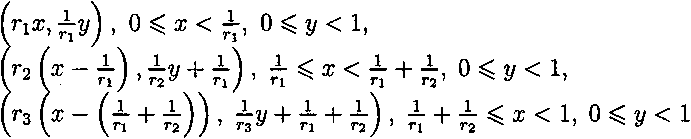
Д = {5 = Ах [0,1)}, В_х = Т"¹В = А₁х\0₁ 1),

А        И              1 1 Л

Ai = —A U — + —A U — Н---Н —А .

ri \П    т₂ / \п т₂ т₃ /

{ ^х, 0 ^ х < ^, ^^-n)’ п ^^ж<п⁺^’ ^(ж-^ + Д)), ^ + £ О<1.

Легко показать, что T_s — точный эндоморфизм, а значит Т — /С-автоморфизм. Здесь F_o = (А х [0, 1)}, Т"¹^ = (Ат х [0, 1)},

А_х = —А U Г1

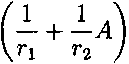
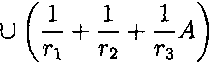
• 3.    Чуть более сложный пример:

  
  
  

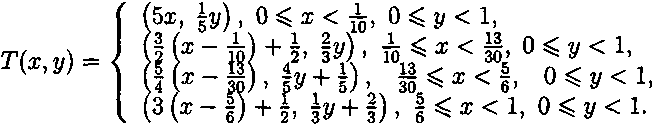
• 4.    Пусть Му = [0, 1) с мерой Лебега

Fo = ^(о,1) х [0, 1), то есть F_o = {В : А у. [0, 1)}. Т^-1В = А_х х [0, 1), где А_т = Т^А, £ — разбиение на х х [0, 1), х € [0, 1) . T_s — точный эндоморфизм, Т — ^автоморфизм.

Т_хх = f^ (modi),

где /(ж) — возрастающая функция, / £ С2 [0, 1), /(0) = 0, /'(ж) ^ 1 + £о ^ж G Мх, для некоторого ер > 0, Нт/(ж) = п £ N или оо. Пусть Ск £ Мх — точки, для которых f(ck) = к, к = 1, п (или к = 1, оо). В силу равенства (2) /(ж) распадается на функции fk(x) = /(ж) — (к — 1), Ск — 1 ^ ж < Ск со значениями в [0, 1), к = 1, п (к = 1, оо). Кроме того, будем считать, что Тх сохраняет меру. Для этого нужно, чтобы если для некоторого у £ [0, 1) выполняется fk^k) = У ^к, то

5 №

должно выполняться равенство

= 1. Т1 — точный эндоморфизм [2]. Теперь на М = [0, 1) х [0, 1) естественным расширением автоморфизма Тх будет Д-авто- морфизм

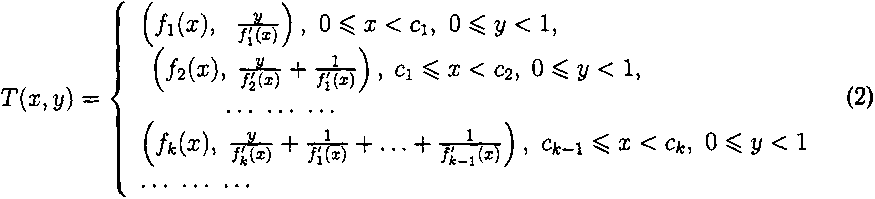
Рассмотрим автоморфизмы, которые не являются К-автоморфизмами, но строятся аналогично им. Возьмем автоморфизм Ту пространства Му = [0, 1):

2т+ j, 0^т<|,

Тух =

2 (^ ~ 4) + 9! 4 ^ ^ < 2’ ’   24’

2 И -   > 7 ^ X < 1.

\      4/ ’4

Пусть М = [0, 1) х [0, 1). Положим

T(x,y) = <

2т + j, ^ , 0 ^ т < |, 0 ^ у < j, (^Т ~ 4) "^ 2’ 2^ + 2) ’ 4 ^ ^Ж< 2’ 2^у<1,

’ 2 х    4’ и у2’

4/ ’ 2 ' 2/ ’ 4                2

Если обозначить Fo = {В = А х [0, 1)}, то аналогично предыдущему бу- дут соблюдаться свойства: Т lF0 С Fo и a U TnFo = F. Однако свойство \п=О )

П T~nF0 = R не выполняется. Это пересечение содержит множества [0, 4 х [0, 1) n=0

и [|, 1) х [0, 1) и совпадающие mod 0 с ними. Поэтому это не будет К-автомор-физмом. Однако это будет тоже естественное расширение эргодического неточного автоморфизма Ту, заданного выражением (3), и поэтому Т эргодический автоморфизм. Здесь Bi = Т^-1В = Ау х [0, 1), где Ai = Т^А.

Возьмем теперь автоморфизм Т₂ пространства Му:

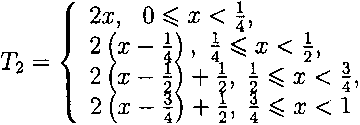
и по нему построим естественное расширение

(2х, ^у), 0^х<^, 0^у<1,

Т(х,у) =

V²^^-Й >^⁺2) ’ ^х<^, 0^у<1, (2 (х - И + Ы , |(х - I) + |, |у + |) , J ^ ж < 1, 0 ^ у < 1.

Это неэргодический автоморфизм, так как имеет инвариантные множества [О, |) х [0, 1) и [|, 1) х [0, 1) меры |. И поэтому Т тоже неэргодический.

Рассмотрим теперь произвольный эндоморфизм Ti отрезка [0, 1), з адан -НЫЙ кусочно-монотонными функциями /к(х), Cfc-1 ^ X < Ск, к = 1, п, О = Со <  Су < ... < с_п = 1; f_k(x) е C4c_k-y,c_fc), \f_k(x)\ ^ 1 + £₀ Для некоторого е₀ > 0. Пусть области значений f_k будут отрезки \а_к,Ьк) С [0, 1). Множество Л = {oi,..., а_п, by,..., b_n^ упорядочим по возрастанию. В результате получим разбиение отрезка [0, 1) на отрезки Д^ = [tZi_i,dj), i = 1, m, где d, G Л, do = 0, d_m = 1.

Тогда положим Т (д, „) - ^(т), ^ ₊ ^ ₊ ... ₊ ^J, х € D_k П Tf¹ А_р+г, 0 ^ у < 1.

Применяя эту формулу для всех непустых пересечений D_k и Tf¹A_i, получаем естественное расширение кусочно-монотонного эндоморфизма Ту. Если Ту будет точным эндоморфизмом, то Г — К-автоморфизмом. Если Ту эргодический (неэргодический), то Т будет таким же.