Estimation of the number of aperiodic words

In 1902 William Burnside raised the question of the local finiteness of groups in which the relation xⁿ = 1 is done [1]. Subsequently, this question acquired the status of Burnside's problem. A negative answer to it was first obtained in 1968 in the works of P. S. Novikov -S. I. Adyan [2– 4].

The group B ( d, n ) with d generators and the identity relation xⁿ = 1 is now called the free Burnside group of rank d and period n . Its finiteness was established at different times for n = 2 (trivial case), n = 3 (W. Burnside [1]), n = 4 (W. Burnside [1] d = 2; I. N. Sanov [5] for arbitrary d ), n = 6 (M. Hall [6]). The proof of the group infinity B ( d, n ), d ≥ 2, for odd exponents n ≥ 4381 was given in [2–4], for odd n ≥ 665 – in the monograph by S. I. Adyan [7].

More details on the results on the Burnside problem can be found in S. I. Adyan [8].

Definition

An l- aperiodic word stands for a word X if it does not contain non-empty subwords type Y^l .

In the A.Yu. Olshansky’ s monograph [10], the theorem on the infinity of the set 6-aperiodic words and a lower estimate for the number of such words of any given length is obtained. The author in [9] improved the estimate from [10] for the number of 6-aperiodic words in an alphabet of two letters.

In view of these results, we consider the set of m -aperiodic words in the two-letter alphabet for m ≥ 2.

The paper [11] also obtained results for 6-aperiodic words over a three-letter alphabet. The author published works [12–15] on this topic. The results can be applied when coding information in space communications.

Main results

In 1906 A. Thue established the existence of non-repeating words in a three-letter alphabet and 3-aperiodic words of random length in any non-one-letter alphabet [11] (see also lemma 1 in [8]). In the paper [16] S. E. Arshon in 1937 proved the existence of an n -valued asymmetric (repeating) sequence for n >  3 . The S.I. Adyan's monograph [7] presents Arshon's method for proving the existence of infinite 3-aperiodic sequences in an alphabet of two symbols.

In [10] Theorem 4.6 on the set of 6-aperiodic words infinity was proved and an estimate was obtained for the f ( n ) function of the number of such words of length n : the alphabet {a, b} contains arbitrarily long 6-aperiodic words. Moreover, the f ( n ) number of such words of length n is greater than ( 32 ) ⁿ .

In connection with these results, it is of interest to estimate the number of m -aperiodic words in a two-letter alphabet.

The case of 2-aperiodic words in the alphabet {a, b} is easily considered and such words can be enumerated at once:

• a , b , ab , ba , aba , bab.

The remaining cases are considered in Theorems 1–3.

When proving the theorems, we will apply the method of A. Yu. Olshansky in [10].

Theorem 1. The alphabet {a, b} contains arbitrarily long m-aperiodic words for m >  5 . Moreover, the number of such words of length n is greater than (32) •

Proof. We first prove the inequality f ( n + 1) >  32 • f ( n ) by induction.

Base of induction: f (2) > 3^ • f (1), where f (1) = 2, f (2) = 4.

Each m -aperiodic word of length n + 1 is the result of assigning one of the letters a or b to an m -aperiodic word of length n on the right. You can obtain 2 f ( n ) words X of n + 1length. However, some of the resulting words may contain degrees A^m . It is necessary to estimate the number of such possibilities.

We can only obtain an equality of the form X = YA^m , since otherwise the beginning of the length n of the word X of n + 1 length already contains A^m . For words A of length 1 (two such words only) there are fewer than 2 f ( n + 1 - m ) words of the form X = YA^m , where the word Y is m -aperiodic and | Y | = n + 1 - m :

(........ aa...a) a, n+1-m m-1

(........ bb ... b ) b.

n + 1 - m    ^{m - 1}

There are 4 words A of length 2. The number of corresponding words of the form X = YA^m of n + 1 length is less than 4 f ( n + 1 - 2 m ), where the word Y is m -aperiodic of the length n + 1 - 2 m .

Similarly, for further reasoning, we have:

f ( n + 1) >  2 f ( n ) - 2 f ( n + 1 - m ) - 2² f ( n + 1 - 2 m ) - 2³ f ( n + 1 - 3 m ) - ...

Since by the induction hypothesis f (n) > (3^)k • f (n - k), we obtain f (n +1) > 2 f (n ) - (2(32)-m+1

Factoring out f ( n ) we obtain

- 2 m + 1

■^{3 m + 1} f ( n ) + ...).

- m + 1

f ( n + 1) >  f ( n )(2 - (2(32) - m ^{+ 1}

- 2 m + 1

’^{3 m + 1} + ...) >  2 -

- m

For any m >  5 (as far as m 2 < ^ for any m >  5 , then the geometric progression in the inequality is decreasing with a denominator 2 ( 3^)   ).

Therefore, the inequality f ( n + 1) >  3^ f ( n ) is true for any natural n for the function f ( n ) of the number m -aperiodic words of length n under m >  5 . The theorem has been proven.

From the proof of Theorem 1, in particular, it follows that this method of proof does not work when proving an estimate for f (n) > (32 ) of the number function f (n) of 3- or 4-aperiodic words of length n. The following theorem shows that this method is not suitable to prove the estimate f (n) > (x)n and for any x value withing the interval [3 2,2] for 3-aperiodic words and out of [4 2,2] interval for 4-aperiodic words.

Theorem 2. Applying the proof of the Theorem 4.6 on 6-aperiodic words from [10] to the case of 3- and 4-aperiodic words does not provide the proof of the corresponding theorem, i.e., for any value of x from the intervals [³ 2,2] for 3-aperiodic and [⁴ 2,2] for 4-aperiodic words cannot be proved by the method from [10] that the number f_m(n) of m-aperiodic words of length n is greater than x n under m = 3 or m = 4 .

Proof. m = 4 . Let us give reasoning similar to those provided in [10]. However, this time we do not fix the value ( 3 / 2 ) n for the base of the exponential function, we introduce the variable x and look for the estimate in the form f ( n ) >  x ⁿ for m = 3 and m = 4 .

We first prove the inequality f ( n + 1) >  x • f ( n ) by induction. At the same time we introduce restrictions on x . To satisfy the inequality f ( 1 ) = 2 >  x for m = 3 and m = 4 , we put x <  2 .

The induction base f (2) >  x • f (1), where f (1) = 2, f (2) = 4. The induction base is valid for x <  2 .

Each 3- or 4-aperiodic word of length n +1 is the result of assigning one of the letters a or b to a 3-aperiodic (4-aperiodic respectively) word of length n on the right. We can get 2 f ( n ) words X of n + 1 length ( m = 3or m = 4). However, some of the resulting words may contain degrees A ³ (degrees A ⁴ respectively). It is necessary to estimate the number of such possibilities.

Only an equality of the form X = YA ³ ( X = YA ⁴ respectively) can be obtained, since otherwise the beginning of length n of the word X with n + 1 length contains A ³ (or A ⁴ ). For words A of length 1 (two such words only) there are fewer than 2 f ( n - 2) (2 f ( n - 3) respectively) words of the form X = YA ³ ( X = YA ⁴ respectively), where the word Y is 3-aperiodical (4-aperiodical) and Y = n - 2 (| Y | = n - 3 respectively):

(........ aa ) a , (........ bb ) b in case of 3-aperiodic words;

n - 2                n - 2

(........ aaa ) a , (........ bbb ) b in case of 4-aperiodic.

n - 3                n - 3

There are 4 words A of length 2. The number of corresponding words of the form X = YA ³ ( X = YA ⁴ respectively) of n + 1 length is less than 4 f ( n - 5) (4 f ( n - 7) respectively), where the word Y 3 is aperiodic of length n -5 (4-aperiodic of length n -7, respectively).

Proceeding with the reasoning in a similar way, we obtain f (n +1) > 2 f (n) - 2 f (n - 2) - 22 f (n - 5) - 23 f (n - 8) -...

for 3-aperiodic words;

f ( n + 1) >  2 f ( n ) - 2 f ( n - 3) - 2² f ( n - 7) - 2³ f ( n - 11) - ...

for 4-aperiodic words.

Since, by the inductive assumption f (n) > xk • f (n - k), it turns out respectively f (n +1) > 2 f (n) - (2( x )-2 f (n) + 22( x )-5 f (n) + 23( x )-8 f (n) +...) and f (n +1) > 2f (n) -(2(x)-3 f (n) + 22(x)-7 f (n) + 23(x)-11 f (n) +...).

factoring out f(n) we obtain f (n +1) > f (n )(2 - (2( x )-2 + 22( x )-5 + 23 (x )-8 +...)

and respectively

f ( n + 1) >  f ( n )(2 — (2( x ) ^{— 3} + 2²( x ) ^{— 7} + 2³ ( x ) ^{— 11} + ...) .

We also introduce restrictions 3/2 <  x in the first case and 4/2 <  x in the second, so that the geometric progressions on the right-hand sides of the inequalities were decreasing.

We denote the second factors of the right-hand sides as S and apply the formula for the sum of the terms of a geometric progression with a denominator 2 x “³ for 3-aperiodic words and 2 x “⁴ for 4-aperiodic words:

^{— 2}

S = 2 ——

1 - 2 x

.— 3 ’

S = 2--2 x 4 .

1 — 2 x

The inequality f ( n + 1) >  x • f ( n ) will hold for S >  x .

We transform the last inequalities for both cases:

_v      2 — 4 x -³

S — x =------

„     2 — 4 x - 4

S — x =------

— 2 x ~2 + 2 x ~2

1 — 2 x “³

— 2 x ~³ + 2 x ~³

1 — 2 x44

—

x

— >  0, under m = 3 ,

—

x

— >  0, under m = 4 .

Upon cancellation we obtain

2 — 4 x ^{— 3} — x

1 — 2 x ^{— 3}

> 0,

2 — 4 x ⁴ — x _л ---------- :    >  0.

1 — 2 x 4

As far as 1 — 2 x ³ >  0 in the first case inequalities: 2 — 4 x ”³ — x >  0 , 2 — 4 x — 4 — x >  0 .

and 1 — 2 x — 4 >  0 in the second, we obtain

We are interested in solutions of these inequalities in the intervals ( ^2; 2 ) and ( ^2; 2 ) , respectively. It turns out that the inequalities in these intervals have no solutions. The theorem has been proven.

As shown in Theorem 2, proof 1 fails for the case m = 4. In the consequent theorem, we prove that the assertion of Theorem 1 is nevertheless true for m = 4. For the case m = 3, the proof by the same method as in Theorem 3 fails.

Theorem 3. The alphabet {a, b} contains arbitrarily long 4-aperiodic words. Moreover, the number f ( n ) of such words of length n is greater than (^) •

Proof. We use the same scheme as in Theorem 1, but we will discard fewer unnecessary words.

.

Note that f (1) = 2 > —

We prove the inequality f ( n + 1) > — • f ( n ) by induction.

Induction base: f (2) > — • f (1), where f (1) = 2, f (2) = 4.

Each 4-aperiodic word of length n + 1 is the result of assigning one of the letters a or b to a 4-aperiodic word of length n on the right. We can get 2 f ( n ) of X words of length n + 1, but some of the resulting words may contain degrees A ⁴ . It is necessary to estimate the number of such possibilities.

We can only get an equality of the form X = YA ⁴, since otherwise the beginning of the length n of the word X of n + 1 length contains A ⁴ . For the words A of length 1 (two words only) there are fewer than 2 f ( n — 3) words of the form X = YA ⁴ , where the word Y is 4- aperiodic and | Y | = n — 3 :

(........ aaa) a n-3

(........ bbb ) b.

n - 3

In fact, among the words Y of the first type we need to take only those that end with b , since otherwise the word in brackets would already contain a ⁴ , which contradicts it 4-aperiodicities. Similarly, among the words Y of the second type we need only those that end with a . Thus, for words A of length 1 there are fewer words than f ( n - 3) words of the form X = YA ⁴ , where the word Y is 4-aperiodical and Y = n - 2.

There are 4 words A of length 2. The number of corresponding words of the form X = YA⁴ of length n + 1 is less than 4 f ( n - 7), where the word Y is 4-aperiodical of n - 7 :

(....... aa aa aa a) a n-7

(....... ba ba ba b) a n-7

(....... ab ab ab a) b n-7

(....... bb bb bb b ) b.

n - 7

However, such words as in brackets of the first and last words are no longer contained in the set of 4-aperiodic words of length n , so they must be removed from this list. In the second word, the subword Y of length n -7 cannot end with a , since otherwise the word in brackets would already contain ( ab )⁴ , which contradicts its 4-aperiodicity. Similarly, in the third word, the subword Y of n - 7 length cannot end with b , since otherwise the word in brackets would already contain ( ba )⁴ . Thus, there are fewer words of the form X = YA ⁴ of length n + 1 than f ( n - 7), where Y is 4-aperiodic word of length n - 7 .

Proceeding with reasoning in a similar way, we get f (n +1) > 2f (n) - f (n - 3) - ((22 - 2) / 2)f (n - 7) - ((23 - 2) / 2)f (n -11) -...

Since by the induction hypothesis f (n) > (3 / 2)k • f (n - k) , we obtain f (n +1) > 2 f (n) - (2 • (3/ 2)-3 f (n) + 22 • (3/ 2)-7 f (n) + 23 • (3/ 2)-11 f (n) +...) + +((3/ 2)-3 f (n) + 2 • (3/ 2)-7 f (n) + 22 • (3/ 2)-11 f (n) +...) +

+ ((3/2) ^{- 7} f ( n ) + (3/2) ^{- 11} f ( n ) + ...)

factoring f(n) out, we obtain f (n +1) > f (n)(2 - (2 • (3/ 2)-3 + 22 • (3/ 2)-7 + 23 • (3/ 2)-11 +...) + +((3 / 2)-3 + 2 • (3/ 2)-7 + 22 • (3/ 2)-11 +...) +

+ ((3/2) ^{- 7} + (3/2) ^{- 11} + ...))

We denote the second factor on the right side as S and apply the formula for the sum of the terms of a geometric progression with a denominator 2

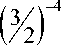
for the first and second progressions and with a

denominator

( 32 Г

for the third:

on    2(3/2) - ³   .   (3/2) — ³   .  (3/2) — 7

S = ²-- 7 +-- 7 +-- 7 .

1 - 2(3/2) - 4   1 - 2(3/2) " 4   1 - (3/2) ^{- 4}

This S value is approximately equals 1,58 which is greater than 3/2. The theorem has been proven.

The following stems directly from the Theorems 1 and 3.

Result. The alphabet {a, b} contains arbitrarily long m-aperiodic words for m >  4 . Moreover, the number of such words f ( n ) of length n is greater than (3/) .

Conclusion

The problem of estimating the number of aperiodic words is still being studied. The set of m -aperiodic words in the three-letter alphabet is considered and an estimate is obtained for the function of the number of such words of any given length.