Evaluation of network parameters of a sensor node deployment strategy in wireless sensor network for hilly terrains

Published Online January 2019 in MECS

Wireless Sensor Networks consist of large number of tiny, inexpensive, low power and resources constrained devices called Sensor Nodes (SN) whose purpose is to sense or monitor changes in critical parameters such as sound, environmental pressure and temperature and communicate the observations locally or to the Base Station (BS) in single or multi-hop routes. WSNs play a vital role in many applications such as health care, environmental monitoring, military surveillance etc. WSNs are prone to adversarial attacks due to a limited amount of memory embedded on Sensor Nodes, lack of fixed infrastructure and uncontrolled environment. Security requirements are mandatory since WSNs are often deprived of human support to maintain secure communication between sensor nodes. WSNs and ad-hoc networks have similar security requirements.

The concern about Coverage, Connectivity and Lifetime together into one simple parameter would help much in evaluation of performance of a designed network. So, Coverage and Connectivity can be considered as basic requirements in a Wireless Sensor Network.

In a WSN when the height of the sensor nodes positions’ is not negligible as compared to the breadth and length of the deployment field it is categorized as three-dimensional (3D). To find an optimal way to localize the sensor nodes on the targeted 3D WSN is the major issue to get the desired degree of coverage and a reliable connectivity on for the chosen field. The solution should yield a lower bound on the number of nodes needed to achieve full coverage with minimum superposition. However, optimization of network parameters such as coverage and superposition in 3D WSNs deals with complex mathematics and its intrinsic design challenges. 3D WSNs are not only difficult to visualize but their analysis is also computationally intensive.

• II.    Related Works

Numbers of sources are used to provide the general background information on this topic. In this section, a brief review of node deployment methods which solves Coverage and superimpose problem in Wireless Sensor Networks and techniques that are used to increase the lifetime using Coverage are discussed.

Sema Oktug and et al, their study went on 3D coverage under the heterogeneous environments for the newly proposed deployment strategies. The answers to questions like how many sensors are needed to cover a specified 3D terrain at a specified coverage percentage were evaluated. Simulation results demonstrate that depending on application requirements an appropriate deployment strategy could be selected to obtain required 3D coverage. [17]

Hassan Chizari and et al, they proposed a Delaunay Triangulation based method to place the sensor nodes on the targeted field which satisfied the value for all coverage measurement tools. The evaluated results proved that the proposed triangulation method achieved accurate coverage information, and provided many tools to compare QoC between different scenarios. [8, 9]

Miao Jin and et al , in ^[13] they tackled the problem of optimal sensor deployment on 3D surfaces, aiming to achieve the highest overall sensing quality. The extensive simulations were conducted on various 3D mountain surface models to demonstrate the effectiveness of the proposed algorithms.

Usman Mansoor and Habib M. Ammari, they summarized major work conducted in the domain of coverage and connectivity in 3D WSNs. The evaluation of the node deployment scheme was shown with five regular space filling polyhedrons: cube, dodecahedron, icosahedron, octahedron, and tetrahedron. [20]

Renan Nespolo and et al proposed a new method for node deployment in a 3D surface which is based on Delaunay triangulation. To obtain maximum coverage area using a minimum number of sensor nodes in threedimensional surfaces the deployment was performed using the dual Delaunay triangulation/Voronoi Diagram. [15]

• S.    Surekha and et al, they used Delaunay Triangulation based deployment for the uncovered region in the WSN. In their work, area coverage problem was considered for irregularly shaped target fields. The Random deployment and Grid-based deployment of sensor nodes was analyzed and compared according to the results obtained. ^[18]

The novelty of the review lies in the different study angles and providing a comprehensive understanding of the coverage and connectivity ^{[1, 4, 6, 7]} in deployment _phase [2, 3, 10, 14] _{in WSNs.}

In literature, the proposed methods considering threedimensional solutions showed relevant results for specific reliefs, indicating that it is possible to propose a flexible method to design a 3D WSN and to solve the problem of maximum coverage on that distinct three-dimensional surface. Based on the review, it may be revealed that computational geometry has a unique advantage on designing 3D Hilly Terrain of a surface and approximate the surface more smoothly which also provide an estimated environment for WSN and sensor node deployment on WSN. Also it has a great advantage on performance evaluation of WSN in terms of coverage of the network dealing with some of the polyhedrons. In this work, a new method is proposed where the design of the network is tried to be solved using geometric modeling as well as the performance of the network.

• III.    Methodology

In this project work, the main aim is to get higher efficiency for a network topology in terms of coverage and superimpose area with respect to sensor count which will increase the network performance and which is at the same time economical. The work can be divided into roughly five phases.

• A.    Phases of the Proposed Method

Phase1: Collection of surface data

Phase2: Generation of the simulated surface using

Delaunay Triangulation

Phase3: Node deployment strategy

Phase4:  Getting the sensor Count and position selection of the sensor nodes

Phase5: Evaluation of coverage and superimpose Area.

• B.    Sketch of the Proposed Node Placement Method

The proposed sensor node placement method for Hilly Surfaces is represented in a flowchart as follow:

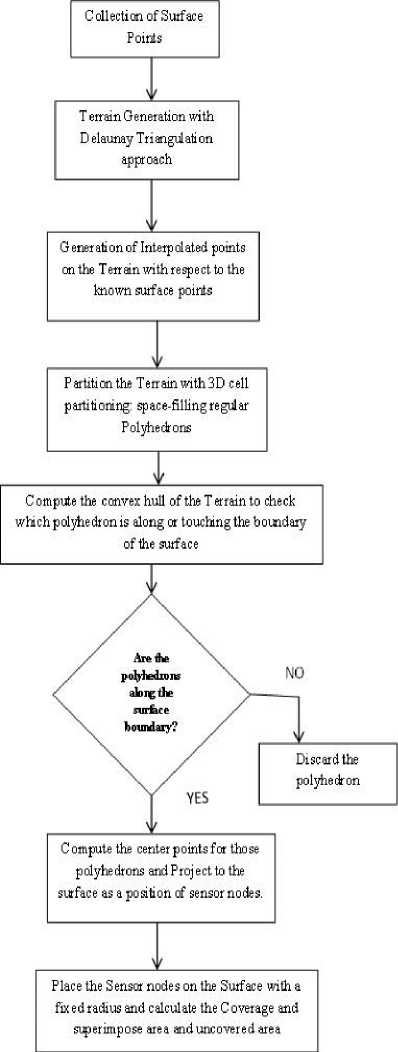
Fig.1. Flowchart of the node placement method

• IV.    Surface Generation

In this section, a hilly earth surface was chosen and made it a computer simulated environment to model the proposed designed approach and for the evaluation and of the model to check the efficiency. For the approximation of an Earth’s surface, the traditional approach of terrain generation was followed with the Delaunay Triangulation approach to generate a terrain of the surface to work on it.

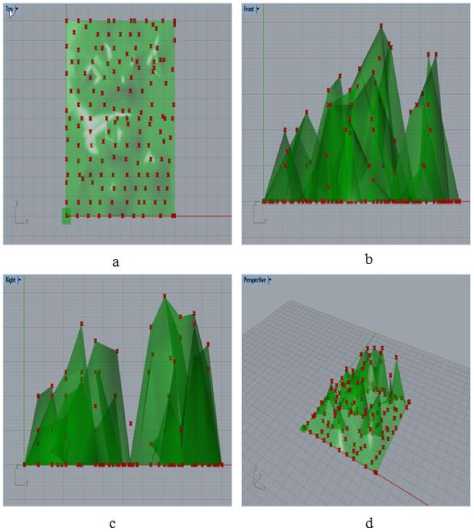
Fig.2. Simulated results for the surface generation with the surface points: (a) Top view, (b) Front view, (c) Right view,

(d) Perspective view.

Total 2D Surface area, T of the surface was calculated in 3D space for each triangulated face generated in the triangulation using coordinate geometry [19].

• V.    Sensor Placement Strategy

Placement of sensor nodes in Wireless Sensor Network is one of the most challenging issues with a limited number of sensors in order to achieve maximum geographical coverage and connectivity among the sensor nodes on a targeted 3D field which dictates the overall network performance. There are various researches going on to improve the sensor placement strategy based on different algorithms.

• A.    Partitioning of the Targeted Field

In this work, a divide and conquer approach was considered to get the sensor count and projection method was used to localize the sensor nodes in the targeted field to get the maximum coverage. Volumetric quotient based approach was used to partition the space where the targeted surface resided. Space was divided by spacefilling polyhedron i.e. cube and centers of the cubes were considered as sensor count which were inside the surface boundary.

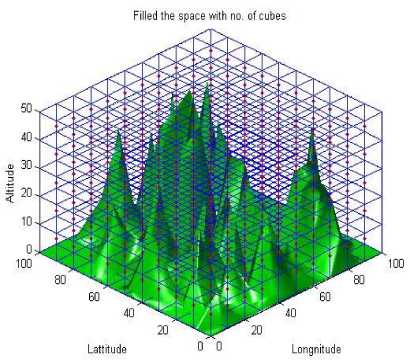
Fig.3. Simulated results for the partitioning of the surface with space filling polyhedrons: cube

_А= ( P 2 - P ) X ( P 3 - P )

Here, P , P , P are the surface points generating a triangulated face in the triangulation.

Total Surface area, t = a + a + a +........+a         (2)

Here A ,A ,A ,........,A is the area of the each triangulated face generated in the triangulation.

• B.    Localization of the Sensors on the Targeted Field

To place the sensor nodes on the targeted field, the projection method was used to get the location of the sensor nodes. After getting the sensor count and the cube centers, the sensors positions were computed through projection method and nodes were placed on the field to get an efficient area coverage and connectivity. In this work, with the same number of sensor count, sensors were placed in two different positions as follows:

• •    Casel : Project to the nearest known surface sample point as the sensor location.

• •    Case2 : Project to the nearest surface point i.e. perpendicular projection.

  

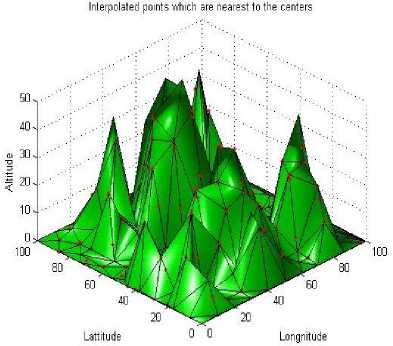
  Fig.4. Sensor locations after projection to the terrain ( Case1 )

  
  
  

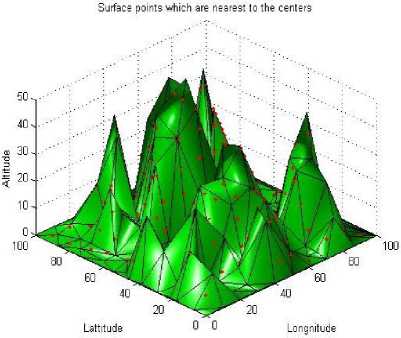
  Fig.5. Sensor locations after projection to the terrain ( Case2 )

  
  

• VI.    Computation of the Parameters

After the placement of the sensor nodes on the targeted field, computation of coverage was done to check the efficiency of the placement method. In this work, geographical coverage was computed as follows:

• A.    Coverage Calculation

To get the actual geographical coverage with the placed sensor nodes, the intersection between the generated surface and the sensing covering spheres were evaluated until intersection area became null. Total coverage was calculated from the union of those intersection areas.

Coverage= Triangulated faces of the surface A Sensor Nodes

Total Coverage Area= ∑Coverage

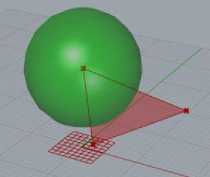
a: Sensor Placed on the Surface

Fig.7. Extraction of intersection area between the surface and the covering spheres with respect to the various positions of the sensor nodes on the surface.

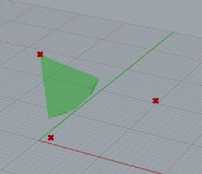
b: Resultant area of Coverage

• B.    Coverage Holes

After projection of the sensors on the field, conflict locations of the sensors were discarded and considered only one sensor localization at a particular point with a fixed covering range.

The uncovered area was evaluated as the coverage holes on the targeted field i.e. the portion where sensor nodes had no coverage. The total uncovered area was calculated by subtracting the coverage area from the total surface area.

Fig.6. Simulated results for the Sensor node placement on the targeted field with a fixed covering range. (a) Top view, (b) Front view, (c) Right view, (d) Perspective view.

Uncovered Area= Surface Area – Total Coverage Area

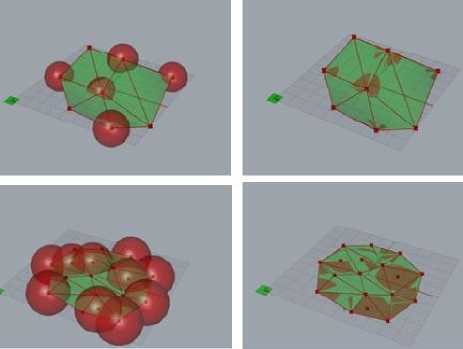
Fig.8. Coverage and coverage holes for the different positions of the sensors on the surface

• C.    Superimpose Area

In this work, superimpose area was calculated as the covering area more than one sensor nodes with respect to the different number of sensor nodes. The intersection of the sensing spheres on the surface was the superimposed area which was extracted until intersection area among the sensor nodes became null as follows:

a

b

If d<2*r; where d is the distance between the sensor nodes and r is the sensing radius then S= Sensor Nodes п Sensor Nodes Superimpose Area= S п Triangulated Surface Total Superimposing Area= ∑Superimpose Area

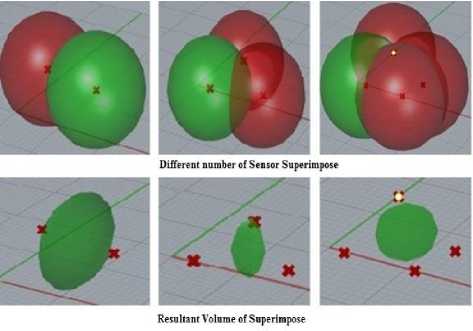
Fig.9. Computation of Superimpose volume with respect to a different sensor count

c

d

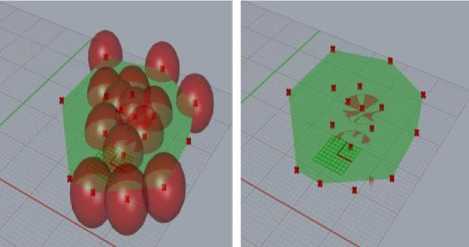
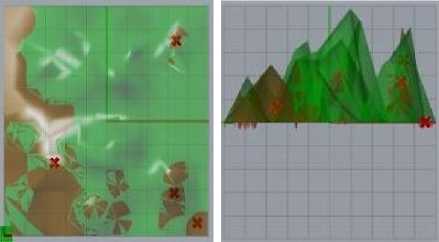
Fig.10. Computation of Superimpose area with respect to superimpose volume on the surface

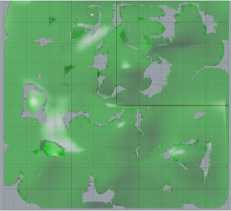
Fig.11. Computation for Area Coverage and Uncovered area for different surfaces (a) Top view, (b) Front view, (c) Right view, (d) Perspective view.

a                       b

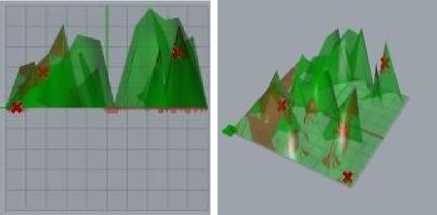
c                        d

Fig.12. Computation for Superimpose area (red) for different surfaces (a) Top view, (b) Front view, (c) Right view, (d) Perspective view.

• VII.    Performance Evaluation

The above mention method was computed for different surfaces with the randomly chosen number of surface points and results found as follows:

• VIII.    Results

  The proposed designed methodology was evaluated using the software MATLAB R2014a. The area coverage and superimpose area and sensor count were calculated for the considered surfaces. A comparison bar graph was prepared for both the deployment methods for four different surfaces and results were presented as follows:

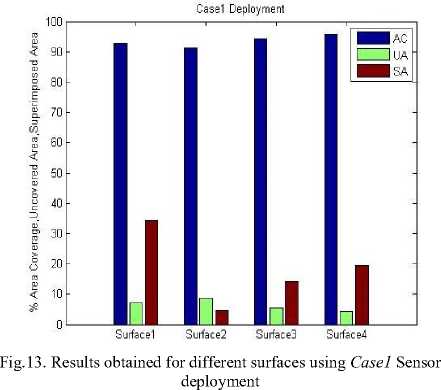
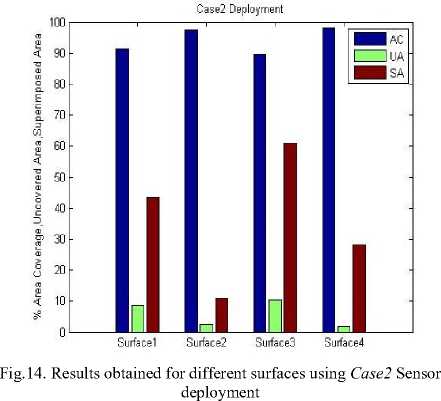
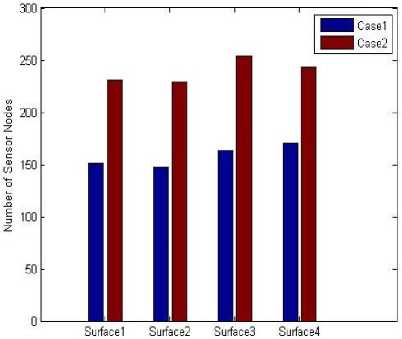
Fig.15. Numbers of sensor count used for different surfaces

• IX.    Conclusion

In wireless sensor network sensor node localization is a major problem which has a great impact on coverage of the sensor nodes on the targeted field. In this paper, a new node placement strategy is proposed and coverage is computed for different surfaces. Depending on the various surfaces chosen, the overall results found are efficient 92% to 95% for both the first method with a superimpose area of 4% to 34% and 89% to 98% for the second method with a superimpose area of 10% to 61% out of total surface area. Observing the results it can be said that the first method gives an efficient result with less sensor count for all the surfaces but the result of the second method varies according to the peaks on the surface with a large number of sensor counts.

The results obtained are promising better geographical coverage with less uncovered area for hilly surfaces. The first method works better for hilly surfaces in comparison to plane surfaces and the second case projection assures full coverage and connectivity for the plane surfaces and which is found to be better than the coverage obtained in [15] considering superimpose area as well and also results obtained for the terrain in [17].

• X.    Discussion and Future Scope

The clear aim of the proposed deployment strategy is to make the network efficient in terms of coverage and sensor count for Hilly Terrains such that case study of this project will help to estimate the node placement strategy to monitor a surface without going to that original place physically.

A work can be extended until it retrieves a good degree of result. The design strategy for this work can be improved with various node placement methods focusing on a particular degree of coverage area against the number of sensor nodes deployed on the surface. In the same way to make the network efficient in terms of energy consumption one can focus to solve superimpose area for the proposed design topology. For every node placement strategy, the following works can be done to improve the efficiency of the network.

• 1.    Superposition of the sensor nodes can be solved and minimized to get an efficient result in terms of energy consumption.

• 2.    Node deployment methods can be varied to check which method is more efficient: Space-filling polyhedrons can be changed in each method.

• 3.    Sensor Count and sensor Location can be tried to improve in each method to check the connectivity as well.

• 4.    For placement of the sensor nodes obstacles can be considered to improve the work in proper manner.