Evolutionary Optimized Neural Network (EONN) Based Motion Control of Manipulator

Published Online November 2014 in MECS

Recently, two important branches i.e. Evolutionary Algorithm (EA) and the Neural Network (NN) of intelligent control schemes has been combined. Combination of these two important branches  of computational intelligence (CI) is necessary and inevitable [1]. Inspite of a great nonlinear learning capabilities and good prediction of Neural Network [2] a list of its disadvantages includes high processing time, prone to generalization and tuning the parameters of the network by trial and error method; which is a time consuming and frustrating task. These limitations of NN restrict its use. Auto adaptability in the system can be one of the solutions and can be made in by using EC intelligent techniques [3]. Hybrid of these NN and EC (used to optimize the parameters of the neural network) has found to be an effective solution to the control problems and hence Evolutionary Neural Networks (ENN) has been generated [4, 5]. Most recently in [6], ENN has been called as the next generation Neural Networks.

Recently, radial basis neural networks (RBNN) have been widely used for non-linear system identification, owing to which RBFNNs have only one hidden layer and have fast convergence speed. Besides, the RBNN are often referred to as model-free estimators since they can be used to approximate the desired outputs without requiring a mathematical description of how the outputs functionally depend on the inputs. RBNN is also known to be a good universal approximator. When utilizing RBNN, some constant parameters must be determined first. A systematic way to determine the initial structure of RBNN must be established. Generally, these parameters are determined according to the experience of the designer or are just chosen randomly. However, such kind of improper initialization usually results in slow convergence speed and poor performance of the RBNN. In [7], Radial Bias Neural Network has been used to find the equivalent torque for the manipulator control system. Similarly, in the control problem defined in this particular problem, single input single output (SISO) RBNN has been proposed. Spread factor (s) is taken as an input to the RBNN and control torque for the system to be controlled is taken as output.

V id = v_id + C 1 e 1 (p^ -x^) + c₂ e₂ (p_xd - x_id ) (1)

^xid = ^xid ^{+ V}id                                       (2)

where, in a D-dimensional space x? = (xi1, xi2, ...x^ ) is a present position vector, p = (Pn, Pi2, —PiD ) is a best position vector, V = (vi1, Vi2,... viD ) is a velocity vector, c is a constant having value 2,

• £₁ and e₂ are the random number generators.

In [10, 11] it has been proved that PSO finds the global best solution. PSO is becoming popular due to its simplicity in implementation and ability to converge quickly to a reasonably good solution.

Robotic manipulator is a highly non-linear, timevarying and highly coupled system. Almost all kinds of control techniques have been discussed in literature [12, 13, 14 and references there in.] for a manipulator, but because of the non availability of accurate mathematical models of manipulator systems; still the thrust for an accurate and precise controller is there. Moreover, manipulator links are driven by actuators. Actuators are connected through either direct drive or gear train. Mainly three kinds of actuators are available: 1) Pneumatic 2) Hydraulic type and 3) Electric motors. Different actuators have different dynamics. Electric motors are more famous because of their light weight and high torque. Moreover controlling of electric motors is much easier than other two actuators. Therefore, for high speed applications usually electric actuators like direct current (DC) motors, induction motors, and brushless DC motors are used. Moreover, the dynamics of most motors remains non-linear and hence popular in robotic applications.

• II.    System Dynamics and Problem Formulation

Performance of the control technique proposed in this work has been checked for position control of a robotic manipulator system with actuator dynamics. In this section, manipulator and actuator dynamics have been given below as;

Manipulator Dynamics:

The dynamics of revolute joint type of robot can be described by following nonlinear differential equation given in (3) [15],

M(q)q + V(q, q) + G(q) = т                   (3)

with q e R n as the joint position variables, т as vector of input torques,

M (q) is the inertia matrix which is symmetric and positive definite,

V(q, q) is the coriolis and centripetal matrix,

G (q) includes the gravitational forces.

Actuator Dynamics:

The dynamics of the armature controller dc motor that drives the link is given by the n decoupled equation.

J M ⁶¹ m + B⁶ m + F M + ^r t = ^K a                    ⁽⁴⁾

where 6_M is the rotor position angle. The control input is the motor voltage vector BeR n the actuator coefficients matrixes are given by:

J M = diag{J m _i}

B = diag{B m _i+K b _iK M _i/R a , }                     (5)

R= diag{r i }

Km = diag{KMi/Ra,} where the ith motor has inertia Jm , rotor damping constant Bm , back emf constant Kb , torque constant KM and armature resistance Ra . The gear ratio of the coupling from the ith motor to ith arm link is ri which is, qi = ri 0Mi                                              (6)

The actuator friction vector is given by

F M = vec{F M _i }                                    (7)

where F_M is the friction of i^th rotor.

Using (7) to eliminate 6_M in (4) and then substituting т from (3) results the manipulator dynamics in terms of joint variables

(J_M + R 2 M)q + (B + R 2 C)q + (RF_M + R 2 F) + R 2 G =

RK m B      (8)

or by appropriate definition of symbols,

M(q)q + V(q,q) + G(q) + F(q,q ) = т           (9)

The complete dynamics (9) has the same form as the robotic manipulator dynamics (3). The complete armplus-actuator dynamics enjoy the same properties as the arm dynamics, all the bound assumptions holds and linearity in the parameters holds. Thus in future work, all the upcoming advance intelligent controllers is used to check their performance with and without actuator dynamics. This is to check the robustness of the controllers.

Problem Formulation:

Control in trajectory tracking means “how do we get the output of the system to follow the input?”. The basic problem in motion control of manipulator is to determine the control inputs necessary to follow, or track a desired pre-planned trajectory. Main challenges in robot motion control problem is the complexity in dynamics and presence of uncertainties especially in high speed operations or while controlling direct-drive robots, for which no gear reduction is available to mask effective inertia variations. A general design for motion control of manipulator has been represented in Figure 1.

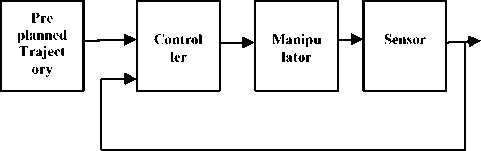
Fig. 1. General Design for Motion Control of Robotic Manipulator

• III.    Problem Solution and Control Schemes

Applied control schemes for the trajectory tracking problem of manipulator can be explained as below.

Acceleration coefficient of actual path covered is given in (10)

q c ̈ = M^-1[τ - V(q, q̇) - G(q)]                   (10)

ė =q̇ -qċ ,Є Rn

• A.    Proportional Derivative (PD) controller in (13) is used for manipulator motion control.

τ=Kpe(t) +Kdė(t)

where, K_p and K_d are suitable positive definite diagonal n x n matrices. Values of the controller constants i.e. K d and K p are being decided by TAE (Trial And Error) method. Data generated in this controller is being stored and used further for the training of RBNN and EONN.

• B.    Radial Bias Neural Network (RBNN) controller

After learning, NN has a capability of generalization and then respond optimally to the unknown situations. Input torque given to the manipulator is very important. In this paper, a RBNN network is trained by using the data of a simple PD controller. Gaussian function is used as the activation function of each neuron in the hidden layer. The excitation values of this Gaussian function are distributed between the input values. The output of the network is given by (14) as

u = ∑jn=1 wj exp

^- IIs-cj II

s2

where j is the j^th neuron of the hidden layer, c j is the central position of the neuron j and s is the spread factor of Gaussian function. This trained RBNNPD is used further to find the output torque to be given to the manipulator. Input given to the NN is spread factor (s) and output is the control torque (τ) to be given to robotic manipulator.

• C. Evolutionary Optimized Neural Network (EONN)

Evolutionary Neural Networks refer to a special class and advance class of a neural networks in which evolution is used for adaptation along with the learning. List of advantages of ENN over NN includes [4]

• •    Avoidance if trapping in local minima of error function.

• •    The fitness function does not have to be differentiable or even continuous.

• •    Better performance in certain problems.

• •    Independence from initial conditions.

A general procedure of EONN is presented in the form of flowchart in Fig. 2 below. The proposed controller in this work can be explained as: spread factor (s) of RBNN is optimized by the improved PSO algorithm. Improvement in the PSO is implemented by varying the

accelerations coefficients (c1 and c2 ) in (1) with time (15) [16]

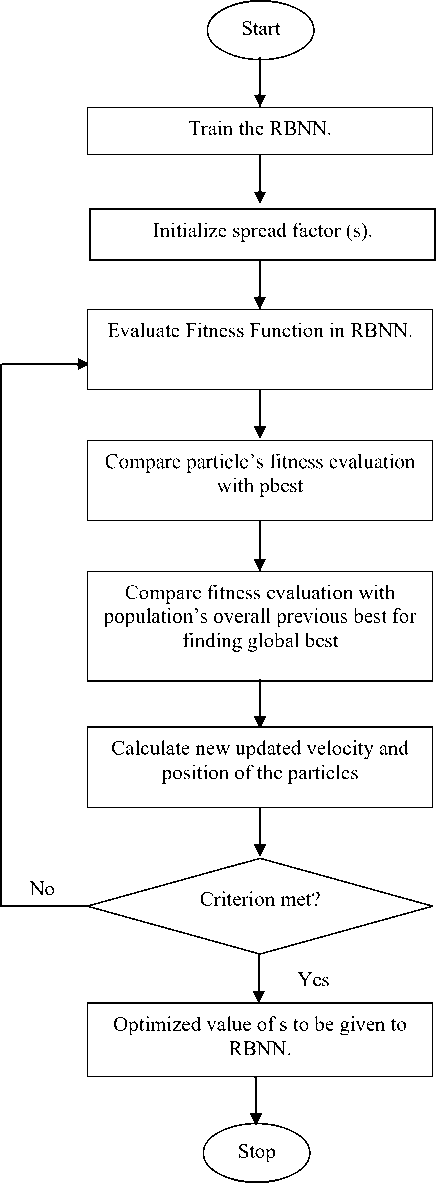
Fig. 2. Flowchart Representing Eonn Working.

c 1 = (c 1f - c 1i ) _ma^it_x^e_it^r_er + c 1i c 2 = (c 2f - c 2i ) _ma^it_x^e_it^r_er + c 2i

(15a)

(15b)

where c1i, c1f, c2i and c2f are constants, iter is the current iteration number and maxiter is the maximum number of allowable iterations.

Value of w which is used in (1) is given in (16)

maxiter -iter w = (wmax - wmin ) (          ) + wmin maxiter

1st trajectory q1 = 0.3 sin(0.7t - n) + 0.3 sin(0.1t - n) + 0.7 (17a) q2 = 0.5 sin(0.9t - n) + 0.5 sin(0.1t - n) + 1.1 (17b) 2nd trajectory q1 = sin(0.67t) + sin(0.3t)

q2 = sin(0.39t) + sin(0.5t)

3rd trajectory q1 = 1.6 - 1.6exp(-8t) - 12.8expE(-8t)

q2 = 1.6 - 1.6exp(-8t) - 12.8exp^(-8t)

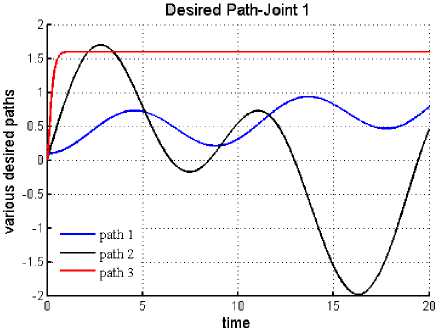
Fig. 3. Desired trajectories: Joint 1.

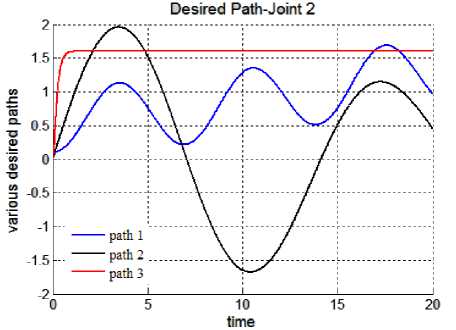
Fig. 4. Desired trajectories: Joint 2.

• IV.    Simulation Example and Results

• 8.77 + 1.02 * cos(q₂)  0.76 + 0.51 * cos(q₂)l

The dynamics of a 2 DOF robotic manipulator taken for this simulation study satisfying (3) is given as

M(q)

= 0.76 + 0.51 * cosi'(q2)            0.62

v(q,q)

• -0.51 * sini^q 2   -0.51 * sini^Xq 1 + q 2 )1

• -0.51 * sini'(q₂)q 1                 0

• 74.48 * sin⁽q 2 ) + 6.174 * sin(q t ) + q 2] G^(q) I         6.174 * sin(q 1 ) + q₂

Parameters of the actuator dynamics discussed above in (5) are chosen as

JM1 = 2.85 kgm2, JM2 = 1.4 kgm2 ,

K M = 19.44 Nm/A , K M = 12.28 Nm/A ,

R_ai = 1.2 П , Ra₂ = 1.3 П, r 1 = r₂ = 1;

B M = 0.0573, B M = 0.0253,

Kb1 = Kb2 = 5 V/rad/sec , FM1 = FM2 = 1.5

For this simulation study two cases have been taken into consideration:

Case 1: without actuator dynamics,

Case 2: with actuator dynamics.

Control gains parameters for PD controller are opted by TAE method as

1000   0          70  0

K p   L 0     200.1 ^;      K d 1.0    50.1 ^;

In RBNN controller, by making about 50 trial runs of TAE methods spread factor is tuned to 2.

In proposed EONN controller, modified PSO parameters are taken as: range of spread factor as (0.10.7); Population size: 30; iterations: 50; wmax = 0.9 and wmin = 0.4; values of c1and c2 are made to change from 2.5 to 0.5 and 0.5 to 2.5 respectively.

Results: Results of all the simulation studies for all the controllers applied on a non linear control problem of motion control of robotic manipulator has been given in Figures 5 & 6. Figure 5 (a-f) contains the trajectory tracked by three controllers for both the joints in Case 2 i.e. with actuator dynamics. It can be observed form the figure 5 that for joints 1 & 2 best trajectory is tracked by EONN. It can also be visualized that RBNN performance is proven to be better than classical PD controller. With PD controller tracking accuracy is least. Same type of results can be observed in Figure 6, which gives the continuous tracking errors. For non linear control problems performance evaluating criteria naming, transient error, steady state error, overshoot time etc. are not sufficient. Hence, for performance evaluations indices like mean error, mean square error (mse) and mean of input control torque have been chosen here. These performance evaluating factors have been tabulated in table 1. It can be observed from the results in the table that in both the cases (with and without actuator dynamics) the errors and control input torques have reduced when EONN controller is used. With actuator dynamics (case 2) errors in all the three trajectories have increased. Moreover, input control torque has also increased in Case 2.

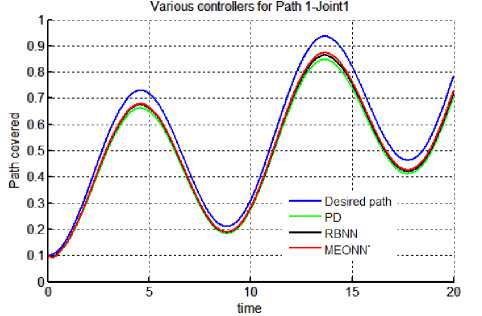
Fig. 5 (a) Trajectory 1: Joint 1.

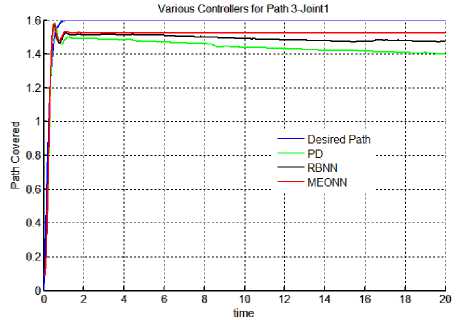
Fig. 5 (e) Trajectory 3: Joint 1.

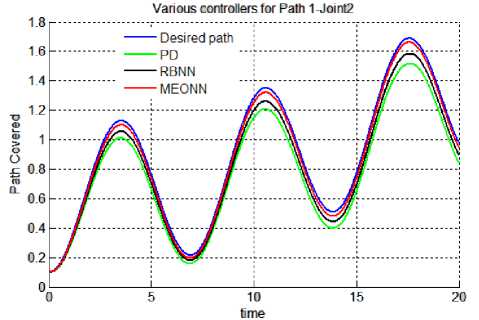
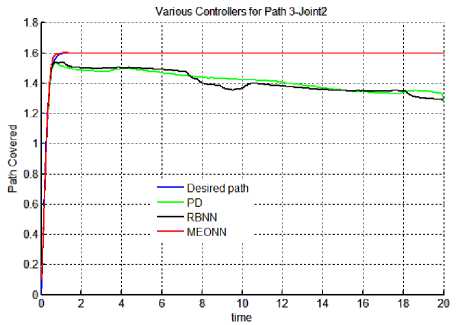
Fig. 5 (b) Trajectory 1: Joint 2.

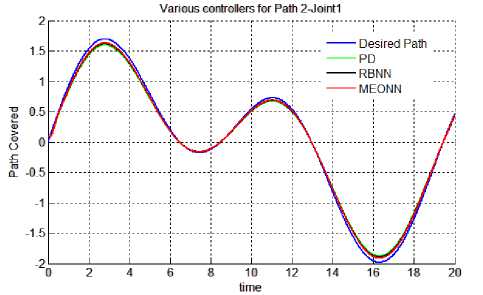
Fig. 5 (c) Trajectory 2: Joint 1.

Fig. 5 (f) Trajectory 3: Joint 2.

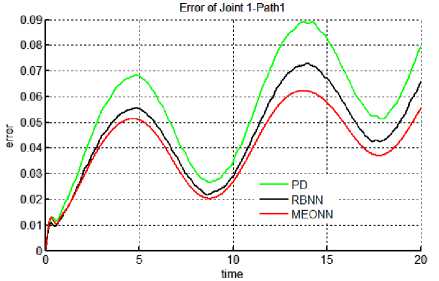
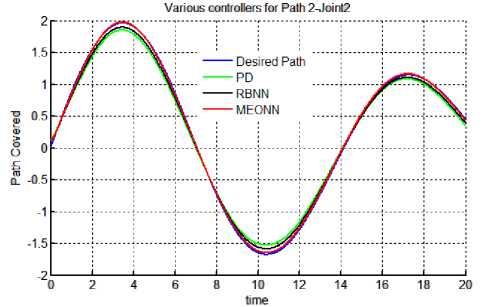
Fig. 6 (a) Trajectory 1: Joint 1.

Fig. 5 (d) Trajectory 2: Joint 2.

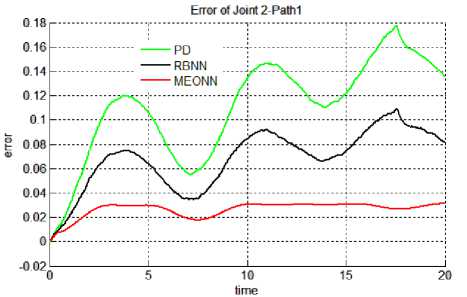
Fig. 6 (b) Trajectory 1: Joint 2.

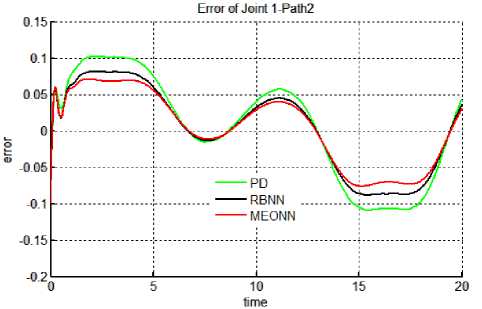
Fig. 6 (c) Trajectory 2: Joint 1.

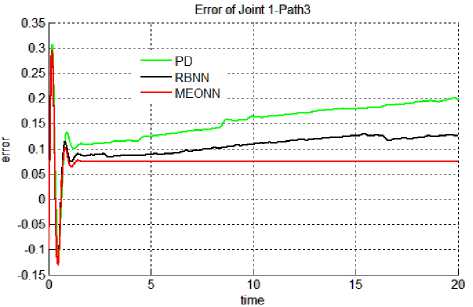
Fig. 6 (e) Trajectory 3: Joint 1.

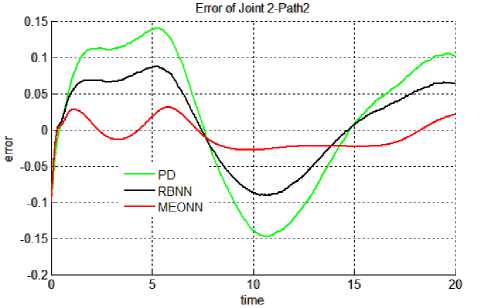
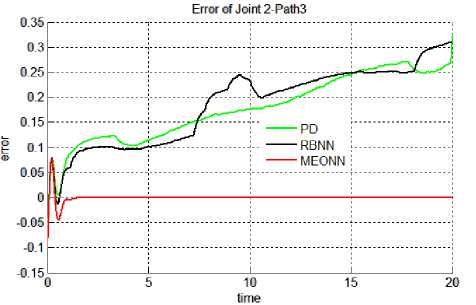
Fig. 6 (d) Trajectory 2: Joint 2.

Fig. 6 (f) Trajectory 3: Joint 2.

		Case 1						Case 2
		mse (e1)	mean (e1)	mse (e2)	mean (e2)	tau 1	tau 2	mse (e1)	mean (e1)	mse (e2)	mean (e2)	tau 1	tau 2
Trajectory 1	PD	0.0034	0.0548	0.0139	0.1107	19600	946	0.021	0.099	0.033	0.34	28078	1289
	RBNN	0.0023	0.045	0.0053	0.0685	19000	923.89	0.011	0.65	0.021	0.099	20875	1007.98
	EONN	0.0018	0.0403	7.33e-4	0.0264	192000	924	0.011	0.521	0.0023	0.0432	17087	980.99
Trajectory 2	PD	0.0051	0.0046	0.0092	0.0241	25700	244.9	0.0087	0.016	0.023	0.043	35767	319.86
	RBNN	0.0033	0.0037	0.0036	0.0109	373.02	241.9	0.006	0.009	0.02	0.032	30876	278.9
	EONN	0.0025	4.40E-4	0.0037	-0.0078	334.75	222.99	0.003	0.00066	0.008	0.01	31098	243.7
Trajectory 3	PD	0.0248	0.1514	0.0357	0.177	466.77	196.7	0.055	0.034	0.088	0.54	564.32	876.88
	RBNN	0.0121	0.105	0.04	0.1841	410	134.7	0.0345	0.23	0.1	0.34	410	576
	EONN	0.0061	0.0735	8.6E-5	9.09E-5	4.4E+2	1.66E+2	0.01	0.001	0.0045	0.0009	2.45E+2	3.57E+2

• V. Conclusion

In this work, intelligent hybrid controller, having a modified PSO to optimize RBNN parameters is proposed. This special class of hybrid controller is named as evolutionary optimized neural network (EONN). Validity of the controllers is checked by implementing it on a 2 dof manipulator. Robustness of the control scheme is checked by taking actuator dynamics into consideration. It has been concluded form the observation made by the results of the simulation study that the proposed EONN controller is giving the best results in terms of minimum errors and reduced required control torque when compared with the classical PD and RBNN controller. Robustness of the controller is checked by implementing the same controller on three different paths. Hence, one can conclude that the proposed EONN control technique has good performance for non-linear control systems. Further improvements in the work can be made by using improvised versions of PSO [17].