Exact solutions in modified gravity theories

1.    Limitations of Einstein General Relativity

Einstein’s General Relativity (GR) theory is a highly successful theory in explaining many issues in cosmology and astrophysics such as (i)the prediction of perihelion precession of Mercury (ii) the deflection of light by the Sun (iii) the gravitational redshift (iv)radar echo delay and (v) the detection of gravitational waves through the binary black hole merger. In GR, it is believed that, a mass causes the space-time to curve and thereby rejects the action at a distance theory as proposed in Newtonian mechanics. GR is basically a geometrical theory based on Riemannian metric tensor д 叮 ,which describes not only the gravitational field, but also the geometry. The action in GR can be written as

N,

(1.1)

where R is the Ricci scalar, д is the determinant of the metric tensor д 叮 .We chose G = c = 1. £团 is the matter Lagrangian. The field equations in GR may be obtained as

The left hand side of this equation describes the geometry and the right hand side considers the matter field through the energy-momentum tensor 厶".The energy-momentum tensor is obtained from the matter Lagrangian £团 as

2 8( 广 Q

，- ?   Sg ""    ,

(1.3)

and its trace by T =疗"厶" .

Einstein’s GR is a beautiful geometric theory, which gives a unified description of gravity as geometric property of space-time. In this theory, the space-time is described by the Riemannian metric

曲 ² = 呢“ dx ^ dx^ ;    〃,〃 = 0 , 1 , 2 , 3 .

(1.4)

We may consider a simple geometry for example a flat Friedmann - Robertson - Walker (FRW) metric given by ds2 = —d力2 + a2(t) (dx2 + dg2 + dz2) ,                             (1.5)

where a(t) is the radius scale factor of the Universe. At the time of the proposition of the General Relativity theory, Einstein considered the Universe to be infinite and static. However, after the discovery of Hubble’s law which states that the recessional velocity is directly proportional to the distance between the ob jects, it is confirmed that, the Universe is not static rather, it is expanding. The rate of expansion of the Universe is usually defined through the Hubble parameter defined as

H = .                                           (1.6)

Q

We are not yet certain about the composition of the matter and/or any other energy components of the Universe. Most of the time, we assume that, the Universe is filled with a non-dissipative perfect fluid described by an energy-momentum tensor

T g^ = (p + p )q U " + pg^

where p is the energy density and p is the pressure of the cosmic fluid. Here, u ^g = 8 g is the four velocity vector.

For the given cosmic fluid and the flat FRW metric, the GR field equations may be obtained as

3H ² = 8ттр 2H + 3H ² = — 8ттр.

(1.7)

(1.8)

These equations are known as the Friedmann equations. The first equation speaks of how the rate of expansion of Universe is related to the matter content (the energy density p) of the Universe and the second one provides us an idea about the cosmic acceleration and its relation to the cosmic pressure p.

The dynamical aspects of the Universe is assessed through a dimensionless parameter called the equation of state (EoS) parameter ^, defined as the ratio of the pressure to the energy density. From the Friedmann equation, it is straightforward to obtain the EoS parameter as

P s =—

P

2H

3H ² .

(1.9)

We may also define a deceleration parameter q = —患 = — 1 —系 .While a positive value of q describes a decelerated Universe, a negative q represents an Universe with its expansion accelerating with time. In terms of the deceleration parameter, the EoS parameter may be expressed as

3 = ； (2q - ¹ ).

(1.10)

From the above equation one may infer that, if q = —1, then we have ® = —1 and if q = — 2, then ® = — 3. Since the cosmic dynamics is described by the EoS parameter and the EoS parameter is controlled by the deceleration parameter, it is more or less certain that, the deceleration parameter decides the cosmic dynamics. It is required that, the energy-momentum of the whole Universe should be conserved at any point of time i.e.工力" = 0. In GR the conservation equation is given by p + 3H (夕 + #)=0,                                 (1.11)

which ensures the conservation of energy-momentum in the theory.

Einstein theory reigned for a long time in addressing many issues in cosmology and astrophysics. Modifications in GR came later with the introduction of scalar field. Amidst the proposal of different modifications of GR with scalar field, the belief was that, the Universe is finite, may be having an origin of time and is expanding, the expansion depending on the matter field present in the cosmic fluid. However, in 1998-99, Riess et al. [1] and Perlmutter et al. [2] have suggested from a lot of cosmological observations on type Ia supernova that, our Universe is not only expanding rather, the expansion is accelerating at least at its late phase of evolution. A lot of observational data support this fact [3–5]. Observational evidences show that the transition from a decelerated phase of expansion to an accelerated one may have occurred at a redshift z _t 〜 1 [6,7]. This bizzare discovery can not be explained by the standard General Relativity. Researchers contemplate an exotic dark energy form ( to be put by hand in the field equations) to explain this late time cosmic acceleration issue. In GR, the dark energy corresponds to a cosmic fluid with low energy density and a negative pressure. Observations indicate that DE has a lion share of 68 . 3% in the mass energy budget of the Universe [8]. Within the purview of GR, this dark energy driven late time cosmic phenomenon can not be explained in tensor modes. As a solution to this, scalar field models are emerged. Additional degrees of freedom in the form of scalar fields are considered in the gravitational action of GR. Chiral cosmological models with multicomponent scalar fields have also been proposed to address this issue [9–11]. All through the proposition of different dark energy models to explain the late time cosmic speed up issue, we are still not certain about the nature and origin of the dark energy. The only information about dark energy at our hand is that it can cluster at large scales and violates some energy conditions. Besides the issue of dark energy and late time cosmic acceleration, in GR, there exists singularity at Big Bang and inside the black holes where the usual Physics losses it structure. These observations have established that, Einstein’s GR may not be the ultimate theory of gravitation.

2.    Geometry Modification of GR

The speculative nature of the dark energy made ways for the alternative gravity models as possible solution to the cosmic speed up phenomenon where the the geometrical part of the GR field equation is modified in such a manner that, the action will contain some arbitrary function of Ricci Scalar R and possibly the trace of the energy momentum tensor T in place of the Ricci scalar appearing in GR. These geometric dark energy models do not require any additional dynamical degrees of freedom as matter fields. Moreover, these modified gravity theories have been motivated from quantum effects. Several modified theories of gravity have been proposed in literature such as /(R) theory [12,13], /(G) gravity [14], /( 丁 ) theory [15,16], /(R,T) theory [17], /(Q) theory [18] and /(Q,T) theory [19]. The most popular among them is the / (R) gravity theory where we have a more general function of the Ricci scalar R replacing the usual R in the Einstein-Hilbert action:

$ =+ / /(R)/^"% + / Lm7—g "4£.

(2.1)

The field equations of the /(R) theory may be written as fRRw — ；/(R)g“" = (▽“ ▽” — g“” ▽“ ▽”) /r (R) + 尺T-,                (2.2)

where /д = ^д^). One interesting aspect of this geometrically modified gravity theory is that, the GR is recovered for /(冗)=R. Also, one gets the ACDM model for a replacement of /(冗)=R — 2Л. Here Л is the cosmological constant. Extension of the /(R) theory with different functional forms of /(R) have been proposed in literature to address different cosmological issues. Caroll proposed the 1/R gravity model with / (R) = R — Д, q being a constant [12]. In this model the late time cosmic acceleration is achieved with the scale factor behaving like。(力) 〜 力2 and the equation of state parameter as ® = — |. This theory is obtained to be similar to scalar-tensor gravity theories such as the Brans-Dicke theory with a Brans-Dicke parameter 3bd = 0. One should recall that, the solar experiments require rather a large value of the Brans-Dicke parameter i.e. ®bd > 20000. Of course, incorporation of time dependence of the Brans-Dicke parameter, a rather low negative value is required. The stability of /(R) theory is assessed through the quantity m = д{дд . If m > 0 , the model is stable and for m < 0, the model is considered to JR be unstable. Clearly, the Caroll’s proposed theory is unstable for R > 0. Such a theory modifies gravity both at the large scale and at local scales and there is absence of matter era. Other popular assumption in /(R) theory is the Starobinsky model where the functional is chosen as /(R) = R + qR2, q being a constant. Starobinsky model was initially proposed to handle the inflationary scenario. Interestingly, the Starobinsky model gravity theories are stable with m > 0. Many other extensions of the /(R) have been proposed in literature.

Later in 2011, Harko et al. [17] proposed an extension of the /(R) theory, with inclusion of the trace of the energy-momentum tensor within the geometrical action:

s =± / /(R,T )V-9 d ⁴ x + / £ _m v— d ⁴ x,

(2.3)

where T =呢"疗" is the trace of the energy-momentum tensor. The matter energy coupling in this /(R, T) theory plays an important role to provide a suitable explanation for the late time cosmic acceleration without the need of any additional dynamical degrees of freedom such as the dark energy. The role of dark energy, in these theories comes from the geometry modification. In /(R, T) theory, the interactions of matter with space time curvature becomes a well motivation to consider different cosmological consequences with varying matter components. However, there remains an issue in /(R, T) theory associated with the non-conservation of the energy-momentum tensor. Josset et al. have shown that, the violation of the energy-momentum conservation in modified gravity theories leads to accelerated expansion [20]. The non-conservation of energy-momentum in the extended gravity theories leads to an additional degree of freedom that provides an explanation of the late time cosmic acceleration and may be associated with the description of particle creation process in the gravitational field. There have been a wide interest and investigations concerning issues in cosmology and astrophysics using the recently proposed /(R, T) gravity theory [21—33]. As a simple extended gravity theory, the /(R, T) theory provides a simple structure but have elegance in addressing many cosmological issues.

There is another method to consider the gravitational interaction. In the teleparallel approach, the basic idea is to replace the metric д^” of the space time by a set of tetrad vectors e^. The tetrad fields generate a torsion which is used to describe the gravitational effects. So in the action, the curvature (R) is replaced by the torsion 丁. Such a theory is dubbed as the Teleparallel Equivalent of General Relativity: the /(T) gravity theory. The action in the teleparallel theory may be written as s          /(T)

+

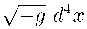
£ 团 d ^— g " £•

(2.4)

A third approach is the representation of the gravitational field through the non-metricity Q where Q geometrically describes the variation of the length of a vector in the parallel transport:

Q 三 -gW[L"%- 券 J&],

where the disformation tensor is defined as

乙誑 = - 2g а 入 [ ▽ ) ^g 户入 + ▽ 户外 7 — ▽ 入 9 户" .

(2.5)

(2.6)

The action of the / (Q) gravity is written as [18]

S = 16^ / / (QZ^-g " 4 £ + / L m<— g d 4 £・

(2.7)

The gravity is called / (Q) gravity or non-metric gravity or symmetric teleparallel gravity. In / (Q) gravity theory, the accelerating expansion is an intrinsic property of the geometry of the Universe, without the need of either exotic dark energy or extra field. The /(Q) gravity is based on Weyl geometry where the gravitational effects do not occur because of the change in the direction of a vector during parallel transport rather due to the change in the length of the vector itself.

In principle, GR can be represented both in the teleparallel representation and curvature representation. Both the geometric representations are equivalent. In the teleparallel representation, the curvature and the non-metricity vanish whereas in the curvature representation, the torsion and the non-metricity naturally remain absent.

Inspired by the success of the / (R,T ) gravity theory, Xu et al. proposed an extension of the symmetric teleparallel gravity by considering a non-minimal coupling between the non-metricity and the trace of the energy-momentum tensor T [19]. The prime motivation behind such a theory is to address the late time cosmic speed up issue where

S = 11^ / /(Q,T)lg" 4 " + / CmQ g d%

(2.8)

All of these geometrically modified theories have their advantages and disadvantages. Many of the theories may not provide stable model and some may not be in conformity with recent observations. In the present work, we consider two specific similar modified gravity theories namely / ( 冗, T) gravity and /(Q, T) gravity. The choice is purely personal. The minimum details of the field equation derivation and extracting information regarding the cosmic dynamics will be presented.

3.    Basic equations and dynamics in f (R,T) gravity

For a minimal matter-geometry coupling within the action, we may split the functional / (R,T ) into two distinct functions /( 冗) and /(T) so that / (R,T ) = /(Д) + /(T) for which the action becomes

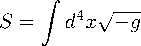
16tt

(/(£) + /(T))+ £ 」 .

(3.1)

The field equations for this geometrically modified gravity theory are obtained through a variation of the action with respect to the metric 呢“

Rs — ； " 1 (R)/(R)m = / R 1 (R) ( ▽ N " — m □ ) / r (R) + [8 冗 + 方 (t )] 小 + 方 (t )p + 2

^g H"

(3.2) where we have considered the matter Lagrangian as £ 团 = —p where p being the pressure of the cosmic fluid. Also, we have used the shorthand notations:

• /R三，方(T)三W， 方阳三鳥.

For a simple linear choice of the function / ( 冗) = R, we get the modified field equations as

• G“"=[断 + 方(T)] T“" + 方(T)p + 2 /(T)]g“",

which can also be written as

Gw = ^ [〃" + T^〔.

Here, 片 丁 = 8тт + / 丁 (Т) is the redefined Einstein constant. Linear choice of the function .方 (T) ensures that, the gravity theory may reduce to the GR under suitable substitution. One should note that, for linear choice, the redefined Einstein constant 片 丁 becomes a constant quantity. However, for any other choices else than a linear one for / т (T) provides us time varying 片 丁 which dynamically mediates the coupling between the geometry and matter. It may be observed that, in (3.5), we have an additional term as compared to the GR field equations which involve an interactive term

T int t 从"

/ т (T )Р + 2 /(Т) ]

87r + / т (Т)   产“

(3.6)

which is the effective energy-momentum tensor generated due to the geometrical modification through a minimal coupling with matter. In fact, this term is the result of the geometry modification of the gravitational action and it shoulders the responsibility for explaining the late time cosmic speed up phenomenon. As emphasized earlier, this matter and curvature coupling is motivated from quantum effects and leads to a non vanishing divergence of the energy-momentum tensor T^ speculating a violation of energy-momentum tensor. At this point, we may chose suitable functional form for /(T) which may provide viable cosmological model and is in conformity with recent observations.

We may consider a simple linear choice

/ (T) = 2AT,

(3.7)

so that

rt = 87r + 2A,

^T- = ^ [ ⑵ ^{+ T} ) ”

(3.8)

(3.9)

The cosmological consequence and the cosmic dynamics of the / (凡 T) may be assessed either considering an isotropic FRW model or through a metric favouring an anisotropic spatial expansion. For the isotropic case, we may use the flat FRW metric in (1.5) for which the equivalent Friedmann equations are obtained as

3Я ² = (87 + 3A)p - Лр, 2H + 3H ² = Лр - (8тт + 3Л)р.

(3.10)

(3.11)

Solving the above equations for the energy density and pressure, we obtain

• —  3(87 + 2Л) H ² - 2ЛН

^P = ~(87 + 3Л) ² - Л ²~ ,

• —    3(87 + 2Л) H ² + 2 (8тт + 3Л) H

^Р =            (87 + 3Л) ² - Л ²         .

The EoS parameter for this model may be obtained as

• — 3(87 + 2Л) H ² + 2 (87 + 3Л) H

ĆJ =--;-------- .

3(87 + 2Л) H ² - 2ЛН

The EoS parameter may be expressed in terms of the deceleration parameter q as

(3.12)

(3.13)

(3.14)

s = - 1 +

8 (27 + Л) (1 + q)

6 (47 + Л) + 2Л(1 + q)

(3.15)

This is an important result in the sense that, the time variation of the deceleration parameter decides the evolution of the EoS parameter. In other words, a constant deceleration parameter leads to a constant EoS parameter.

In the limit of GR, we have А т 0 and the EoS parameter reduces to

ĆJ

2 方

3 Я ² .

(3.16)

In order to investigate the cosmic dynamics, we need to solve Eq.(3.14). Solution may be obtained in different approaches. Suppose we consider a Universe with a constant Hubble parameter i.e. Я = constant. This will lead to a de Sitter kind of Universe with exponential expansion of the scale factor. For such a case, it is clear from Eq.(3.14) that, ® = — 1 as it should be for a de Sitter expansion. We may adopt two different methods to obtain the exact solutions to the equivalent Friedmann equations: either we chose an EoS parameter ( may be constant or time varying) and solve Eq.(3.14) to get the Hubble parameter and then integrate it to obtain the scale factor which will provide us the expansion of the Universe through the ages. On the other hand, we may chose a Hubble parameter or scale factor basing upon certain plausible assumption or constructed from observations and then obtain the EoS parameter which will provide us the cosmic history from an early age to the late times. Also, we get the cosmic dynamics through out the expansion history.

In this work, we will review some of the techniques to obtain the exact solutions with the framework of the / ( 冗, T) gravity theory. We consider some specific choices either for the EoS parameter of the Hubble parameter to obtain the cosmic dynamics. Our goal is to show that, exact solutions for this extended gravity theory can be obtained with simplified approaches with interesting results.

• (i)    Case-1 : Let us chose an EoS parameter: ® = 0 representing a dust Universe. For this case, the field equation becomes

₇Я + Я ² = 0,                                   (3.17)

which can be integrated to obtain

Я = /                                      (3.18)

and consequently the scale factor may be obtained as q ⑴=О                                (3.19)

Here we have defined 7 = 38+2^ . This case predicts a Universe with power law expansion.

• (ii)    Case-2 : Let us now chose a presumed dynamics of the Universe through the choice of a specific scale factor or Hubble parameter or a deceleration parameter such as a periodic varying deceleration parameter (PVDP) [34]:

q = m cos kt — 1,

(3.20)

which yields a Hubble parameter

k

^Я = m cos kt + k i ,

(3.21)

where m is an enhancement factor that enhances the peak of the PVDP and k decides its periodicity. k i is an integration constant and may be fixed from a comparison with observational results. For such a choice, it is straight forward to obtain the cosmic dynamics or the dynamical parameter such as the energy density, pressure and the EoS parameter as

夕

P

ćj

2Am cos kt + 3(8тт + 2А)

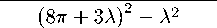
k ²

m ² sin ² kt

2(8tt + 3A)m cos kt — 3(8тт + 2A) (8тт + 3A) ² — A ²

k ²

m ² sin ² kt

2(8tt + 3A)m cos kt — 3(8тт + 2A) 2Am cos kt + 3(8тт + 2A)

(3.22)

(3.23)

(3.24)

Obviously, these dynamical parameters periodically vary with some frequency determined from the parameter к.

• (ii)    Case-3 : For a symmetric bounce scenario, we may consider a scale factor

Q ⑴=户，

(3.25)

(3.26)

(3.27)

/3 being an open positive parameter. The Hubble parameter for this scenario becomes H = 213t.

The energy density 夕 and pressure p for the present model are obtained as [35]

夕

P

123 2 (8 冗 + 2A)t ² - 43 入

(8 冗 + 3X) 2 - X ² ,

123 2 (8 冗 + 2X)t ² + 43 (8 冗 + 3X)

(8 冗 + 3X) 2 - X ²

From the energy density and pressure we may get the equation of state parameter for this symmetric bounce model as

123 2 (8 冗 + 2X)t ² + 43 (8 冗 + 3X)

(3.28)

123 2 (8 冗 + 2X)t ² - 43X

Here we get a symmetric bounce of the model at t = 0. Also, the EoS parameter is symmetric about the bouncing epoch. One interesting aspect is that, there is no ® singularity near the bouncing point.

• (ii)    Case-4 : We may consider a hybrid scale factor (HSF) that simulates a transitioning Universe with early deceleration and late time cosmic acceleration considered through the Hubble parameter [36, 37]

H = 3 + I ，                                  (3.29)

where i and 3 are constrained from the observational Hubble parameter data. The HSF is an intermediate between a power law expansion and exponential expansion and is suitable for the investigation of cosmological issues.

The dynamical parameters of the model may be obtained as

P  = (断 + 3 X ) 2 — _X 2 t 2 [ 2Xi + { 3(3t + i) ² } 師 + 2X) ] ,                   (3.30)

P   =  &     q \ 2—\2 ； 2 [ 2(8 亓 + 3X)i - { 3(3t + i) ² } 師 + 2X) ] ,           (3.31)

(8 穴 + 3X ) X t

2i                                                 ,

® = — 1 + (8 冗 + 3X )—----；——----匸------ —.                        (3.32)

2 Xi + { 3(3t + i) ²} (8 冗 + 2X)

Here the EoS parameter decreases quadratically to the concordant ACDM value at late times i.e ® T — 1 as t T 2

In a similar manner, we may assume any given background dynamics and from it, the EoS parameter may be reconstructed using the technique as described above.

4.    Basic Equations and Dynamics in f (Q,T) gravity

The field equations of the / (Q, T) gravity may be obtained as

2       , 一 —    、     1 _

— у— ^ V a (后 ^- ^乜 " ) — 2 禽 h"

+ f _T (!> + Ө “" ) —f _Q ( P>3Q 产 — 2Q” aB” ) =8 亓 T>.            (4.1)

Here Ө ^" = g “° ^^ and we have used the short hand notations

/ 三 /QT ）； 三 ； 三 =

^ = P ， = - 2 Ь ^^ + 4 ( Q “ - Q “ ) 9 нн - 4 b^Q " ) is the superpotential for the model.

For a flat FRW metric ds2 =-必2 + a2(t)Sij dk d岔 3,(4.2)

we get

Q = 6W ² .

We consider a perfect fluid distribution of the Universe so that

Ti 三 d沁g (-p,p,p,p), and

Oij = bjp — 2Ti 三 d沁g (2p + p, —p, -p, —p).

We have now

T + 6ij 三 diag (p + p, 0, 0, 0).

The field equations for the / (Q, T) gravity for the given FRW metric and the perfect fluid are obtained as

16 冗 p

16 冗 p

/ - 12ҒЯ ² +4 ( 厂卜

- / + 12ҒЯ ² + 4*.

(4.6)

(4.7)

Here, * = FH and ;* = FH + FH . b = 1 + 霆 .The evolution equation may be obtained as

* = 4 不 8 ⁽ p + p) .

(4.8)

We may express the field equations in /(Q, T) gravity as

3H 2 = 迎 F 2H + 3H 2 = F

/      1 岁 + 5 ((1 ― b ) p ― bp) = Weff ,                     (4.9) 32 穴 2 + 9 ((1 + b ) p + bp )          = - ^p eff .             (4.10) 32 万    2                 4 万

The effective equation of state parameter may now be expressed as

•

•

3 二 & 二 _{- 1+} 4 ( 亓 一 8)FH - 2FH °" ^peff          / + ¹⁶ 冗 [ ^{(1 - b ) p} - A^p]

(4.11)

Let us consider a simple coupling of the non-metricity and the trace of the energy-momentum tensor:

/ (Q,T) = A i Q + 毋,

(4.12)

where A i and A 2 are some chosen constants so as to obtain a viable cosmological model. For a flat FRW metric we have Q = 6H ² and T = 3p - p, so that /(Q, T) = 6A 1 H ² + A 2 (3p - p), F = 器 =A i ; / r =鳥= ^A 2 ^{; b} = ^{1 +} 誥 / = ^ 2 .

We wish to consider different cases to obtain the exact solutions in the /(Q, T) gravity theory as we have discussed for the / ( 冗, T) gravity theory.

(i) Case-1 : We may chose a barotropic relation such as p = p(p) so that we have ® = ^ . The simplest case is the dust case: p = 0, ® = 0. For such a dust Universe within the /(Q, T) gravity theory, we get the energy density as

p

^{3 A} 2    ^2

2 (A 2 + 478) ,

(4.13)

so that the evolution equation becomes

я

np

67AA 2

A i ( 》 2 + 4ttS)

я 2 .

(4.14)

The above relation may be written as

я n,

Я ²      ,

(4.15)

where n

6 行入入 2

A i (A 2 +4^A) .

On integration, we obtain a dynamics of the form

'n 力 + О

.

(4.16)

(4.17)

The corresponding scale factor becomes

。⑴ =a 。 (n 力 + 0)1"

.

(4.18)

In this case we obtain a power law model for the Universe.

• (ii ) Case-2 : Let us now consider a barotropic relation p = ®p with ® = 0. For this choice, we have

  /

  X

  
  

6А і Я ² + A 2 (3® - 1) p 47rs(1 + ®)p,

(4.19)

and the effective cosmological constant may be obtained as

® eff = ^{- 1}

8А 1 Я

6А 1 Я ² + [16tt[(1 - 8)® - 8] + 入 2 ( 3® - 1)] p

(4.20)

From the field equations we may have

5A i

^p — [ 1678 [ 1 - (宁) ® ] - A 2 (3® - 1) ]

я ² .

(4.21)

A substitution of the above equation in Eq.(4.20), we get

® eff

•

-1 - 8 я

— 1 + 8(1 + q).

(4.22)

(4.23)

For a de Sitter kind of model, we have q = - 1 and obviously, ® _e ff = - 1. In order to ensure a negative value of the effective cosmological constant, i.e. ® eff < 0, we may set a condition for the deceleration parameter q as

7 g< ^- 8.

(4.24)

• (iii ) Case-3 : Some more examples may be considered where we try to obtain the exact solution by choosing a Hubble parameter. From the field equations, we may obtain the expressions of the pressure and energy density as [38]

  = 3 》 i H ² + % 方 [1 + 8 - &i]

  '        2 亓[ (1 + 8) 2 +4_Ғ ]  ,

  —  - 3X8 ² + А і Я[3е - (28 + W) &]

  
  

  ^P         2 亓[ (1 + 8) 2 +4— 2 ]

  
  

  ,

  
  

  (4.25)

  (4.26)

  
  

where W = 誥 and & = X

The equation of state parameter may now be obtained using the relation з = ^ :

3А і Я ² + А і Я[1 + 8 - WW i ]

(4.27)

- 3 入必 ² + 入必 [3W - (28 + W) W i ]

We may incorporate some choices of the Hubble parameter into the expressions. For example consider a constant Hubble parameter: H = % for which we have

³ eff

	/ (Q,T)=		A i Q + A 2 T, 6A i H 2 + 8(3p - p).			(4.28)
Obviously we obtain F = |f = 尢; We may express the field equat 3H 2 = ¥ A i		方 = It = a 2 ； X = FH = 入 1 H 0 ; X = 0; ions in /(Q, T) gravity as 6MH 2 + 8 (3 P - p ) + |((1 - 8) p - 8p) 327          2		• F	=0 and A = Weff ，	二 1 + A 2 . (4.29)
2H + 3H 2 =	87r A 1	6MH 2 + 8 (3 P - p ) + |((1 + 8) p + 8p) 327          2		=	- aP eff .	(4.30)
For the present case, we	have
	(1 — 8) p — 8p (1 + 8) p + 8p		=P — 8 ( P + p) = P, = p + 8(p + p) = p.			(4.31) (4.32)

Here we have used the evolution equation 1 + A 2 Now the effective equation of state parameter becomes

P eff ^p ff

2H + 3H ²

3H 2

- 1.

(4.33)

• (iv)    Case-4 : For an HSF, H = q + 号 ,we may use Eq. (4.20) to obtain the cosmic dynamics in the form of the EoS parameter. Alternatively, we may consider Eq.(4.27) to assess the dynamical behaviour of a model throughout the cosmic evolution as worked out in Refs. [38, 39]. Other suitable choices of scale factor may be considered to address different issues and to study different scenario at different evolutionary phases of the Universe.

Besides the use of the functional as in Eq. (4.12), we may consider different choices of the functional /(Q, T) such as

• 1.    /(Q,T)= XiQ^m + ^T,

• 2.    /(Q,T)= AiQ^m+》2丁2,

• 3.    /(Q,T) = AiQ + A2Q²+ 2A3T,

5.    Conclusion

for investigation of different cosmological issues within the framework of the /(Q, T) gravity.

Here we review the limitations of Einstein general relativity in the context of the observations concerning the late time cosmic acceleration. It is certain from observations that, the Universe is not only expanding but its expansion is accelerating. This accelerating expansion of the Universe is believed to be a recent phenomena. Interesting thing is that, till date, we do not have a clear answer for the reason behind the acceleration. In this context, we discuss the perspectives of different geometry modifications of GR. We consider two geometrically modified gravity theories namely / ( 冗, T) theory and the /(Q,T) theory and discussed different simplified techniques to obtain exact solutions for different cosmic scenarios. The two gravity theories are similar in nature also provide similar results. One may note that, a simple modification of the action through the geometry part significantly changes the dynamics of the evolution of the Universe. The structure of these extended gravity theories may be simple but they can be able provide elegant results concerning different issues in cosmology.