Exponential stability for a swelling porous-heat system with thermodiffusion effects and delay
Автор: Douib M., Zitouni S.
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 2 т.25, 2023 года.
Бесплатный доступ
In the present work, we consider a one-dimensional swelling porous-heat system with single time-delay in a bounded domain under Dirichlet-Neumann boundary conditions subject to thermodiffusion effects and frictional damping to control the delay term. The coupling gives new contributions to the theory associated with asymptotic behaviors of swelling porous-heat. At first, we state and prove the well-posedness of the solution of the system by the semigroup approach using Lumer-Philips theorem under suitable assumption on the weight of the delay. Then, we show that the considered dissipation in which we depended on are strong enough to guarantee an exponential decay result by using the energy method that consists to construct an appropriate Lyapunov functional based on the multiplier technique, this result is obtained without the equal-speed requirement. Our result is new and an extension of many other works in this area.
Swelling porous, well-posedness, thermodiffusion effects, delay term, exponential stability
Короткий адрес: https://sciup.org/143180464
IDR: 143180464 | УДК: 517.955.8 | DOI: 10.46698/y2253-0872-2762-l
Текст научной статьи Exponential stability for a swelling porous-heat system with thermodiffusion effects and delay
In this paper, we study well-posedness and exponential stability for a swelling porous-heat system with thermodiffusion effects and delay. The system is written as
P i U tt - a i U xx - a 2 ^ xx = 0 ,
P 2 V tt — а з ^ хх — a 2 U xx — Y 1 9 x — Y 2 P x + Д 1 V t + №V t ( x, t — т ) = 0 , c9 t + dP t - k6 xx — Y i V xt = 0 , ^d9 t + rP t — hP xx — Y 2 V xt = 0 ,
where ( x,t ) € (0 , 1) x (0 , + ro ) , and we impose the following initial and boundary conditions
|
u(x, 0) = u o ( x ) , u t ( x, 0) = u 1 ( x ) , |
x € (0 , 1) , |
|
V(x, 0) = V o ( x ) , V t ( x, 0) = V i ( x ) , |
x € (0 , 1) , |
|
9(x, 0) = У о ( х ) , P ( x, 0) = P o ( x ) , |
x € (0 , 1) , |
|
V t ( x, - t ) = f o ( x,t ) , |
t € (0 , т ) , |
|
u (0 , t ) = v(0, t ) = 9(0, t) = P (0 ,t ) = 0 |
( V t ^ 0) , |
|
_u x (1 ,t ) = V x (1,t) = 9 (1 ,t ) = P (1 ,t ) = 0 |
( V t ^ 0) , |
where u = u ( x, t ) is the displacement of the fluid and y = y(x, t ) is the elastic solid material; p i and p 2 are the densities of u and y, respectively; 9 = 9(x, t) is the temperature difference and P = P ( x,t ) is the chemical potential; k and h are heat and mass diffusion conductivity coefficients, respectively. The coefficients a i , а з are positive constants and a 2 = 0 is a real number such that a 1 a 3 > a 2 2 . The coefficients µ 1 is positive constant and µ 2 is a real number. Here, we prove the well-posedness and stability results for the problem (1)–(2), under the assumption
№ > l ^ 2 | . (3)
The physical positive constants γ 1 , γ 2 , r, c and d satisfying
A = rc — d 2 > 0 .
Equations (1) 1 , 2 are results of the basic field equations for the theory of swelling of onedimensional porous elastic soils, given by (see [1])
f P i u tt = T i x - P i + F i , [P 2W = T 2 x - P 2 + F 2 ,
where T i are the partial tensions, F i are the external forces, and P i are internal body forces associated with the dependent variables u and ϕ, respectively. We assume that the constitutive equations of partial tensions as follows
T i = a i a 2 u x
V T2) Va 2 a 3 / XXM ’
M where M is a positive definite symmetric array, i. e., a22 < a1a3, and the internal forces of the body are considered null, that is, Pi = P2 = 0. We finally chose
F i =0 and F 2 = Y i 9 x + Y 2 P x - ^ i ^ t - ^ 2 ^ t ( x,t - т ) .
Time delay equations have a wide range of applications in the biological, mechanical social sciences, and many other modelling of the phenomena. It depend not only on the present state but also on some past occurrences. We know the dynamic systems with delay terms have become a major research subject in differential equation since the 1970s of the last century (e. g. [2–8]). It was shown that delay is a source of instability unless additional conditions or control terms are used (see [9]). On the other hand, it may not only destabilize a system which is asymptotically stable in the absence of delay, but it may also lead to will posedness (see [10, 11] and the references therein). Therefore, the stability issue of systems with delay plays great importance theoretical and practical in most of researches. In [8], the authors considered (5) by taking
Pi = P2 = 0, Fi = —^i^t — ^2^t(x,t — т) and F2 = 0, they proved that the energy associated with the system is dissipative, and established the exponential stability of the system. Readers can consult [12–20] and the references therein for some other crucial results on the swelling porous system.
The purpose of this work is to study system (1)–(2), in introducing the delay term and thermodiffusion effects can make the problem different and crucial among the literature considered. The main features of this paper are summarized as follows. In Section 2, we adopt the semigroup method and Lumer–Philips theorem to obtain the well-posedness of system (1)–(2). In Section 3, we use the perturbed energy method and construct Lyapunov functional to prove the exponential stability of system (1)–(2).
2. Well-Posedness
In this section, we prove the existence and uniqueness of solutions for (1)–(2). As in [7], we introduce the new variable
z ( x, p, t ) = ^ t ( x, t - тр ) , x E (0 , 1) , p E (0 , 1) , t > 0 . (7)
Therefore, problem (1) takes the form
P i U tt - a i u xx - a 2 ^ xx = 0 ,
P 2 V tt - а з ^ хх - a 2 U xx - Y 1 9 x - Y 2 P x + №V t + Mx 1 , t ) = 0 ,
-
< TZ t ( x, p, t ) + Z p ( x,p,t )=0 , (8)
c9 t + dP t - k6 xx - Y i ^ xt = 0 ,
,d9t + rPt - hPxx - Y2^xt = 0, with the following initial and boundary conditions
|
u ( x, 0) = u o ( x ) , u t (x, 0) = u 1 ( x ) , ^(x, 0) = ^ o ( x ) , V t ( x, 0) = ^ i ( x ) , 9 ( x, 0) = 9 o ( x ) , P ( x, 0) = P o ( x ) , < z ( x,p, 0) = f o ( x,Tp ) , z ( x, 0 ,t ) = V t ( x,t ) , u (0 ,t ) = v (0 ,t ) = 9 (0 , t ) = P (0 ,t ) = 0 _u x (1 ,t ) = V x (1 ,t ) = 9 (1 ,t ) = P (1 ,t ) = 0 |
x E (0 , 1) , x E (0 , 1) , x E (0 , 1) , ( x,p ) E (0 , 1) x (0 , 1) , (9) ( x,t ) E (0 , 1) x (0 , + ro ) , ( V t > 0) , ( V t > 0) . |
Introducing the vector function U = ( u, u t , z, v, v t , 9, P) T . Then system (8)-(9) can be written as
( U ‘ ( t ) = AU ( t ) , t > 0 ,
\
(U (0) = Uo = (uo,ui,^o , vi,fo,9o,Po)T, where the operator A is defined by
/ Ut u ut ^ ϕt z 9 P
P 1 1 [ a i U xx + a 2 ^ xx ]
ϕ t
A
P 2 [ а з V xx + a 2 U xx + Y 1 9 x + Y 2 P x - mV t - №z( x, 1 , t )] - T z p ■
( ^ ) 9 xx - ( hd ) P xx + ( rY 1 - dY 2 ) V tx
V ( ch ) P xx - ( kd ) 9 xx + ( c22^ ) V tx )
Now, the energy space is defined by
H = Hi(0,1) x L2(0,1) x Hi(0,1) x L2(0,1) x L2 ((0,1),L2(0,1)) x L2(0,1) x L2(0,1), where
h 1 (0, 1) = f e H 1 (0 , 1); f (0)=0) .
Let
U = (u,u t ,4,4 t ,z,9,P) T , U = (u,U t ,4,4 t ,z,9,P) .
Then, for a positive constant ξ satisfying
TЫ < € < T <2 № - W,
we define the inner product in H as follows
( U U ) H = j [ p r u t u t
+ a i U x U x + p 2 ^ t 4 + а з Ч х Ч х + a 2 x 4 x + 4 x U x) ] dx
1 11
+
/
[c99 + d^P9 + 9P) + rPP] dx + €
II z ( x,p) .. ....
The domain of A is
d (A ) = {U e H | u, Ч e h 2 (0, 1) , u t , ч e h 1 (0, 1) ,
9, P e h1(0, 1), z, Zp e L2( H2 Clearly, D) is dense in H. We have the following existence and uniqueness result. Theorem 1. Assume that Uo e H and (4) holds, then problem (7)-(8) exists a unique solution U e C<R+; H). Moreover, if Uo e D), then U e C (R+; D<A)) П C1(R+; H) . <1 To obtain the above result, we need to prove that A : D (A) ^ H is a maximal monotone operator. For this purpose, we need the following two steps: A is dissipative and Id — A is surjective. Step 1. A is dissipative. For any U = (u,ut,4,4t,z,9,P)Te D), by using the inner product and integrating by parts, we obtain (AU, U^h — k j 9X dx — h j Px2dx — (w—2T)/ 0 ϕt2dx — — — I z2<x, 1, t) dx. 2T J Using Young’s inequality, we obtain —^2 j z Therefore, from the assumption (11), we have {AU, U)h < k θx2dx (№ —2t V) / ^2 dx — h j Px2 dx — ^2— ^т^^ / z2(x, 1, t) dx ^ 0" Consequently, A is a dissipative operator. Step 2. Id — A is surjective. To prove that the operator Id — A is surjective, that is, for any F = (fi,..., f7)T€ H, there exists U = (u,ut,v,Vt,z,9,P)T € D(A) satisfying (Id — A )U = F, which is equivalent to u — ut = fi, P1Ut — aiUxx — a2Vxx = Pf2, V—Vt = f3, < p2Vt — a3Vxx — a2Uxx — Yi9x — Y2Px + ViVt + №z(x, 1, t) = P2f4, (13) TZ + Zp = Tf5, X9 — rk9xx + hdPxx — (rYi — dY2) Vtx = Xf6, ^XP — chPxx + kd9xx — (cY2 — dYi) Vtx = Xf7. Suppose that we have found u and ϕ with the appropriate regularity. Therefore, the first and the third equations in (13) give J ut = u — fi, Vt = V — f3 . It is clear that ut € H1(0,1) and Vt € H1(0, L). We note that the fifth equation in (13) with z(x, 0, t) = vt(x,t), has a unique solution z(x, p, t) = v(x)e Tp — ρ f3(x)e-Tp + те-тр j eTsf5(x,s) ds, 0 clearly, z, zp € L2((0,1) x (0,1)). By using (13), (14) and (15) the functions (u, v, 9, P) satisfy the following system piu — aiuxx — a2Vxx = gi, nv — a3Vxx — a2uxx — Yi9x — Y2Px = g2, X9 — rk9xx + hdPxx — (rYi — dY2)Vx = дз, XP — chPxx + kd9xx — (cY2 — dYi)Vx = g4 , where П = Р2 + № + №e T, gi = pifi + pi f2, < g2 = P2f4 + пfз - P2Te-T / eTsf5(x, s) ds, дз = —f6 - (rYi — dY2 )f3x, ,g4 = —f7- (cY2 - dYi) f3x• We multiply (16)i by u, (16)2 by (, (16)з by c9, (16)4 by rP, (16)з by dP and (16)4 by d9 and integrate their sum over (0,1) to find the following variational formulation B ((u, (, 9, P)T, (u, (, 9, P)T) = G(u, (, 9, P)T, (17) where B : [H^O, 1) x H^O, 1) x L2(0,1) x L2(0,1)]2—> R is the bilinear form given by B ((u,(,9,P)T, (u, p,6,P)T) = pi У uu dx + ai j 11 1 + п У (p dx + аз У (xpxdx + c j 99 dx + k j 9x9xdx + uxuxdx+a2/■xux+uxpx) dx +d 0 00 r j PP dx + hj PxPxdx У (вР + P9) dx + Yi j (9px - (x9) dx + 72 j (Ppx - (xP) dx, and G : [Hi(0,1) x H* (0,1) x L2(0,1) x L2(0,1)] —>R is the linear form defined by 11 1 1 11 T cr dd G uH^pJdP3) = giH dx + g2(5 dx + — дз9 dx + — g4P dx + — дзP dx + — g49dx. 00 0 0 00 It is easy to verify that B is continuous and coercive, and G is continuous. So applying the Lax– Milgram theorem, we deduce that for all (u, (p, 9), P) G H(0,1) x H(0,1) x L2(0,1) x L2(0,1), problem (17) admits a unique solution (u, (, 9, P) G Hi(0,1) x Hi(0,1) x L2(0,1) x L2(0,1). The application of the classical regularity theory, it follows from (16) that (u, (, 9, P) G H2(0,1) x H2(0,1) x H0)(0,1) x H0)(0,1). Hence, the operator Id - A is surjective. Consequently, the result of Theorem 1 follows from Lumer–Phillips theorem (see [21, 22]). ⊲
3. Exponential Stability In this section, we prove the exponential decay for problem (8)–(9). It will be achieved by using the energy method to produce a suitable Lyapunov functional. We define the energy functional E(t) as E(t) = 2/ + aiux + p2(t + аз(х + 2a2ux(x + c9 + 2d9P + rP ] dx + 2 У У z2(x,p, t) dpdx. Noting (4), we have for 9, P = 0, c92 + 2d9P + rP2 = -92 + r (-=9 + VTp)2 > 0, then we get that the energy E(t) is positive. The stability result reads as follows. Theorem 2. Let (u, z,^,9,P) be the solution of (8)-(9) and (4) holds. Then there exist two positive constants k0 and k1, such that E(t) ^ koe-k1t(V t > 0). Before defining a Lyapunov functional, we need some lemmas as follows. Lemma 1. Let (u, .,^,9, P) be the solution of (7)-(8) and (4) holds. Then, the energy functional, defined by equation (18), satisfies 11 1 1 dt E(t) ^ -k J 9X dx - h J Px dx - Ci j 00 0 ^t dx — C2j z2(x, 1,t) dx ^ 0, where Cl = ^ - M - A > 0, C2 = — - —> 1 ' 2 2- ’ 2 2- <1 Multiplying (8)1, (8)3, (8)4 and (8)5 by ut, ^t, 9 and P, respectively, and integrating over (0, 1) with respect to x, using integration by parts and the boundary conditions, we obtain dt 2 j (piut + aiuX + P2^t + аз^Х + 2a2UxPx + c92 + 2d9P + rP2) dx 0 11 1 1 = -kj^ dx - hjPx dx - ^1j ^tdx - ^2 у ^^.(x’ 1’t) dx. 00 0 0 On the other hand, multiplying (8)2 by Tz(x,p,t) and integrating over (0,1) x (0,1), and recalling z(x, 0, t) = ^t, we obtain ξd ξ 2 dt / z (x’ P’t) dPdx = 2? ^t dx - 7— j z2(x, 1,t) dx. A combination of (21) and (22) gives dt E(t) = -k У 9Х dx - h У Px2dx - (^1 - 2?) / ^2 dx 0 - 2- J z2(x, 1, t) dx 0 - p2 j ptz(x, 1,t) dx. Now, estimate the last term of the right-hand side of (23) as follows —^2 j z(x, 1,t)^t dx ^ ^t2- j z2(x, 1,t) dx + y2j ^2 dx. Substituting (24) into (23), and using (11), we obtain (20), which completes the proof. > Lemma 2. Let (u, z,^,9,P) be the solution of (8)-(9). Then the functional Li(t) = —pi j uut dx, satisfies, for any Ei > 0, the estimate 1 21 + Eij Фх dx. Li (t) ^ —Pi У u2dx + ^ai + 4"2”) j 0 10 <1 By differentiating Li(t) with respect to t, using (8)i and integrating by parts, we obtain L1(t) -ρ1 j u2 dx + ai j uX dx + a2 uxϕx dx, then, by Young’s inequality, we obtain the result. > Lemma 3. Let (u, z,^,9, P) be the solution of (8)-(9). Then the functional L2(t) = aiP2 ϕϕt dx - a2ρ1 ϕutdx, satisfies, for any E2 > 0, the estimate L2(t^ ^ — 2 ^ ^x dx + Ci(e2) ^ ^t dx + £2 ^ ut dx +----- 0 00 + ^Ы f px dx + ^x f z2(x, i,t) dx, a a θx2dx where a = aia3 — a2 > 0, Сз(е2) = aiP2 + ^a^^i + a^. a 4е2 < By differentiating L2 (t) with respect to t, using the equations (8)i and (8)2 , and integrating by parts, we obtain L2(t) = -a j V2 dx + aip2У ^2 dx — a2Pi j Vtut dx + Yiai jtp9xdx + Y2ai ϕP dx - µ1 a1 ϕϕtdx - ^2ai У ^z(x, 1,t) dx, 0 where a = „301 established. > - a? > 0. Using Young’s and Poincare inequalities, estimate (26) is Lemma 4. Let (u, z, y, 6, P) be the solution of (8)-(9) and (3) holds. Then the functional L3(t) — alP2 [ ytudx — a2 a3ρ1 utϕ dx, a2 satisfies, for any £3 > 0, the estimate L3(t)<—ai у u? dx+ „3 /yX dx + 2017? t6d dx . - • P. dx a2 a2 + C2(£3) У y? dx + a1^2 f z2(x, 1,t) dx + a22 ε3 ut2dx, where C4 (£3) = 2 a22 1+ -— 4ез a1 ρ2 - a2 a3ρ1 . <1 By differentiating L3 (t) with respect to t, using the equations (8)1 and (8)2, and integrating by parts, we obtain L3(t) — —ai J* Ux dx + „3 J* yX dx + Y1a1 - µ1a1 ϕtu dx a2 a2 /6Xu dx + Y2 1 Pxu dx a2 - P?a1 У z(x, 1, t)u dx + ^ a1P2 - a3ρ1 a2 Using Young’s and Poincare inequalities, estimate (27) is established. > Lemma 5. Let (u, z, y, 6, P) be the solution of (8)-(9) and (3) holds. Then the functional L4(t) — У У е-2трz2(x,p, t) dpdx, satisfies, for some positive constants n1 and n2 , the estimate L4(t) C —n1 j j z(x,p, t) dpdx — n2 j z(x, 1,t) dx +—У y? dx. <1 By differentiating L4(t) with respect to t, and using the equation (7)з, we obtain L4(t) - 2 У J e 2Tpz(x, p, t)zt(x, p, t) dpdx — — У У e-2Tpz(x, p, t)zp(x, p, t) dpdx - — M dh (e 2Tpz2(x, p,t)) dpdx — 2 У У e-2Tpz2(x, p, t) dpdx < -n1 z2(x, p, t) dpdx - n2 У z2(x, 1,t) dx +— У p2 dx, 0 which gives the estimate (28). > Now, we turn to prove our main result in this section. < Proof Of Theorem 2. We define the Lyapunov functional L(t) by L(t) :— NE(t) + ^ NiLi(t) + L4(t), i=1 where N and N (i — 1, 2, 3) are positive constants that will be chosen later. By differentiating L(t), exploiting (20) and (25)-(28), we get L‘(t) ^ — [piNi - ε2N2 - E3N3] у ut2dx - т N3—(a1+41) N1 u2xdx CiN —C3(E2)N2—C4(E3)N3-- τ ϕt2dx - [2 N2 — a3N3—E1N1] У Vx dx kN — 22^ N2 — 2a1Yl N3] Z @x dx — [hN — 2^ N2 — 2^^ N3I Z Px2 dx a a22 x a a22 x - ni J j z2(x,p,t) dpdx — [^N + n2 - a 2a1p2 a22 At this point, taking Ei — 1/Ni, i — 1, 2, 3. We then choose Ni large enough so that Ni > 2/pi. After that, we select N3 so that a1 a22N1 — N3 —( ai +4— JNi > 0. Then, we choose N2 large enough so that j N2 — a3N3 — 1 > 0. Finally, we select N large enough so that C1N - C3(E2)N2 - C4(E3)N3> О, τ kN - 2аЫ N - 2 N > о, aa hN - -' ■ N - 20172 N, > о, aa C2N + П2 - 2 N2 - 2 '2 N, > 0. aa Consequently, from the above, we deduce that there exist a positive constant α0 such that L‘(t) < -aoE (t). On the hand, it is not hard to see that L(t) ~ E(t), i. e., there exist two positive constants ai and α2 such that a1E(t) ^ L(t) ^ a2E(t) (Vt ^ 0). Combining (29) and (30), we obtain that L‘(t) ^ -kiL(t) (Vt > 0), where ki = aa2 • A simple integration of (31) over (0,t) yields L(t) ^ L(0)e-k1t (Vt ^ 0). It gives the desired result of Theorem 2 when combined with the equivalence of L(t) and E(t). >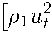
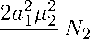
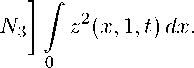
Список литературы Exponential stability for a swelling porous-heat system with thermodiffusion effects and delay
- Iesan, D. and Quintanilla, R. Existence and Continuous Dependence Results in the Theory of Interacting Continua, Journal of Elasticity, 1994, vol. 36, no. 1, pp. 85-98. DOI: 10.1007/BF00042493.
- Apalara, T. A. Well-Posedness and Exponential Stability for a Linear Damped Timoshenko System with Second Sound and Internal Distributed Delay, Electronic Journal of Differential Equations, 2014, vol. 2014, no. 254, pp. 1-15.
- Choucha, A., Boulaaras, S. M., Ouchenane, D., Cherif, B. B. and Abdalla, M. Exponential Stability of Swelling Porous Elastic with a Viscoelastic Damping and Distributed Delay Term, Journal of Function Spaces, 2021, vol. 2021, pp. 1-8. DOI: 10.1155/2021/5581634.
- Kafini, M., Messaoudi, S. A., Mustafa, M. I. and Apalara, T. Well-Posedness and Stability Results in a Timoshenko-Type System of Thermoelasticity of Type III with Delay, Zeitschrift fur Angewandte Mathematik und Physik, 2015, vol. 66, no. 4, pp. 1499-1517. DOI: 10.1007/s00033-014-0475-9.
- Mustafa, M. I. A Uniform Stability Result for Thermoelasticity of Type III with Boundary Distributed Delay, Journal of Mathematical Analysis and Applications, 2014, vol. 415, no. 1, pp. 148-158. DOI: 10.1016/j.jmaa.2014.01.080.
- Nicaise, S. and Pignotti, C. Stability and Instability Results of the Wave Equation with a Delay Term in the Boundary or Internal Feedbacks, SIAM Journal on Control and Optimization, 2006, vol. 45, no. 5, pp. 1561-1585. DOI: 10.1137/060648891.
- Nicaise, S. and Pignotti, C. Stabilization of the Wave Equation with Boundary or Internal Distributed Delay, Differential and Integral Equations, 2008, vol. 21, no. 9-10, pp. 935-958. DOI: 10.57262/die/1356038593.
- Ramos, A. J. A., Almeida Junior, D. S., Freitas, M. M., Noe, A. S. and Dos Santos, M. J. Stabilization of Swelling Porous Elastic Soils with Fluid Saturation and Delay Time Terms, Journal of Mathematical Physics, 2021, vol. 62, no. 2, pp. 1-10. DOI: 10.1063/5.0018795.
- Datko, R. Not All Feedback Stabilized Hyperbolic Systems are Robust with Respect to Small Time Delays in their Feedbacks, SIAM Journal on Control and Optimization, 1988, vol. 26, no. 3, pp. 697-713. DOI: 10.1137/0326040.
- Datko, R., Lagnese, J. and Polis, M. P. An Example on the Effect of Time Delays in Boundary Feedback Stabilization of Wave Equations, SIAM Journal on Control and Optimization, 1986, vol. 24, no. 1, pp. 152-156. DOI: 10.1137/0324007.
- Racke, R. Instability of Coupled Systems with Delay, Communications on Pure and Applied Analysis, 2012, vol. 11, no. 5, pp. 1753-1773. DOI: 10.3934/cpaa.2012.11.1753.
- Apalara, T. A. General Stability Result of Swelling Porous Elastic Soils with a Viscoelastic Damping, Zeitschrift fur Angewandte Mathematik und Physik, 2020, vol. 71, no. 6, pp. 1-10. DOI: 10.1007/s00033-020-01427-0.
- Bofill, F. and Quintanilla, R. Anti-Plane Shear Deformations of Swelling Porous Elastic Soils, International Journal of Engineering Science, 2003, vol. 41, no. 8, pp. 801-816. DOI: 10.1016/S0020-7225(02)00281-1.
- Choucha, A., Boulaaras, S. M., Ouchenane, D., Cherif, B. B., Hidan, M. and Abdalla, M. Exponential Stabilization of a Swelling Porous-Elastic System with Microtemperature Effect and Distributed Delay, Journal of Function Spaces, 2021, vol. 2021, art. ID 5513981, pp. 1-11. DOI: 10.1155/2021/5513981.
- Keddi, A., Messaoudi, S. A. and Alahyane, M. Well-posedness and Stability Results for a Swelling Porous-Heat System of Second Sound, Journal of Thermal Stresses, 2021, vol. 44, no. 12, pp. 1427-1440. DOI: 10.1080/01495739.2021.2003274.
- Murad, M. A. and Cushman, J. H. Thermomechanical Theories for Swelling Porous Media with Microstructure, International Journal of Engineering Science, 2000, vol. 38, no. 5, pp. 517-564. DOI: 10.1016/S0020-7225(99)00054-3.
- Quintanilla, R. Exponential Stability for One-Dimensional Problem of Swelling Porous Elastic Soils with Fluid Saturation, Journal of Computational and Applied Mathematics, 2002, vol. 145, no. 2, pp. 525-533. DOI: 10.1016/S0377-0427(02)00442-9.
- Quintanilla, R. Exponential Stability of Solutions of Swelling Porous Elastic Soils, Meccanica, 2004, vol. 39, no. 2, pp. 139-145. DOI: 10.1023/B:MECC.0000005105.45175.61.
- Quintanilla, R. On the Linear Problem of Swelling Porous Elastic Soils with Incompressible Fluid, International Journal of Engineering Science, 2002, vol. 40, no. 13, pp. 1485-1494. DOI: 10.1016/S0020-7225(02)00021-6.
- Wang, J. M. and Guo, B. Z. On the Stability of Swelling Porous Elastic Soils with Fluid Saturation by one Internal Damping, IMA Journal of Applied Mathematics, 2006, vol. 71, no. 4, pp. 565-582. DOI: 10.1093/imamat/hxl009.
- Goldstein, J. A. Semigroups of Linear Operators and Applications, Oxford Mathematical Monographs, New York, The Clarendon Press, Oxford University Press, 1985.
- Pazy, A. Semigroups of Linear Operators and Applications to Partial Differential Equations, New York, Springer, 1983.


