Fault Tolerant Message Efficient Coordinator Election Algorithm in High Traffic Bidirectional Ring Network

Published Online December 2012 in MECS DOI: 10.5815/ijitcs.2013.01.02

A coordinator could be initiator of an activity (e. g. reconstruction of lost Token in a Token Ring network), recognizer of the deadlock or failures, the root of a spanning tree [2] and it also needed in applications such as video conferencing and multiplayer games.

Coordinator algorithms have lots of usages in different research areas such as Ad Hoc networks [3, 4].

These algorithms are based on different network topologies, process communication strategies, and whether to assign a unique number to processes or not. Network topologies could be directional ring, bidirectional ring, directional graph, mesh graph or it could be dynamic network such as wireless networks and etc. processes can be referenced by unique numbers or by no ones. One of the reasons for not setting a unique number to the processes is because when the number of the system processes increases, the probability of setting a unique number to them will be decreases which will convert it to harder activity. Moreover type of communication between processes can be synchronous or asynchronous.

The reminder of the paper is organized as follow: Related works are discussed in section 2. Section 3 describes system’s assumptions. In section 4 three kinds of message formats which can be used for coordinator election are introduced and section 5 is dedicated to describe our algorithms. The proposed algorithm is simulated and evaluated in section 6 and 7, its convergence is approved in section 8 and finally last section is devoted to paper’s conclusion.

• II.    Related Work

Many algorithms have been proposed for electing coordinators, such as ring [5], bully [6], Chang and Robert [7], Franklin [8], and many other ones. R.Bakhshi [9, 10] proposed an algorithm for electing coordinator in a network which based on assumptions that numbers aren’t assigned to any processes and process’s fault probability is zero. The algorithm of Highman [11] is useful in networks that processes have no number and the numbers of network’s processes is specified at start up time also. Burns [12] and Fich [13] algorithms are based on networks with central demon as scheduler, like Highman [11] processes don’t have any numbers and the number of processes is determined at the start up time. Zargarnataj [14] presented an algorithm that elects assistant for the coordinator as well, so if the coordinator failed, it won't be necessary to launch new election, this algorithm isn’t based on special topology so could be applied to any network. Effatparvar [15] modified bully algorithm to alleviate exchanged message numbers during election and also ring algorithm to apply fault tolerance to it by choosing another process as surrogate coordinator. Shirali [16] proposed an algorithm to improve election performance in the bidirectional ring topology which creates groups of processes, distributes the election in them, and then it compared group’s coordinator with each other to elect the main coordinator afterward. Gholipour [17] introduced another algorithm based on Bully which elects k alternatives in addition to coordinator. After coordinator failure, alternatives are replaced as coordinator in the system, so there won’t be any need to launch new election until k-1 alternatives will fail (this idea is used in this paper’s algorithm). Ingram [18] proposed an algorithm for based on reliability attribute which nodes are reliable but communication links aren’t. He models the entire system by finite state machine that nodes communicate through shared events which could be links up/down, receipts of a message or sending a message. Lots of other algorithms such as [19-21] are also proposed, however, from all of these algorithms Bully and Ring are the two most valuable ones. In contrary of typical ring algorithms, token isn’t used by Ring election algorithm. Its first assumption is that any process just knows its successor and processes and they also referenced by unique numbers. Ring algorithm launches new election after failing the last coordinator by two steps: Each process which figures out the failure of the coordinator must create an Election packet and collect all active processes numbers. When the packet comes back to informer process, it’ll elect coordinator, make a Coordinator packet, and broadcast new coordinator’s number to the network. The algorithm in the worst case is from O (n2) and on average and best case is of O (nlogn). If two processes realize coordinator failure at the same time, the numbers of packets will be twice more but the speed of election won’t change. Effatparvar et al [22] presented another algorithm based on ring topology which makes the packet’s size passed throw the network smaller by considering just a section for informer, but it also causes denying coordinator fault tolerance. Moreover they reduce the number of exchanged message when more than one processes simultaneously find crash out, but if other processes find it out during coordinator crash time and the time which processes know about new elected coordinator they’ll launch new election. This will be worse when more processes find the crash out, especially in high traffic networks.

In the real world, when a process knows its successor and gives packets from its previous process in ring topology, it can figure out its predecessor simply by saving its delivered packet information. Therefore, we work on bidirectional ring topology where each process can communicate to its successor and predecessor. Xie et al, [23] presents an algorithm based on bidirectional ring network. This algorithm is similar to ours in the point of view of sending election messages simultaneously by processes which find coordinator crash out to their successor and predecessor. The election speed is more than simple Ring algorithm and its differences with ours are listed as follow:

• 1)    It inherits the disadvantage of Ring algorithm which is occurred when more than one process find out that coordinator crashed. Hence if n processes find it out the number of exchanged messages will be 2n.

• 2)    It doesn’t care about coordinator failure tolerance in network to avoid any losses in the network’s functions. Therefore the number of exchanged

messages by this algorithm is same as simple Ring algorithm.

The algorithm which is proposed in this paper is based on bidirectional ring too; it appreciates coordinator election’s speed and applies coordinator failure fault tolerance to the network by electing an alternative as well.

• III.    System Assumption

The system which is based by our algorithm has the following characteristics:

• •    Network’s topology is bidirectional ring.

• •    Communication links are reliable.

• •    There is no priority for each process to be elected as coordinator.

• •    Each process just knows its successor and predecessor and doesn’t have any information about other network’s processes.

• •    Unique numbers are assigned to processes.

• •    Message’s format can be differing in the case of network usages and system requirements.

Our election algorithm’s packets have label, so system’s messages such as controlling message could easily throw in the network

• IV.    Message Format

Message’s format which depends on networks characteristics could be any of the below three.

• 1)    N sections format: there are N processes in the network and they add their numbers to message when they receive it. Message passing is very fast by this format but size of the packet goes larger and larger

by increasing the number of process. The format is shown in Fig. 1.

Pn

Pn-1

. . .

p2

Pl

Fig. 1: N Section message format

• 2)    Two sections format: Coordinator and informer numbers are placed in the message. If process number be larger than coordinator’s number, it’ll be placed in coordinator number section. Message has small size but fault tolerant isn’t considered when coordinator crashed and also one compare by each process is required.

Fig. 2: Two section message format

Three sections format : It is obvious that during election each process should check its number with surrogate coordinator number in addition to coordinator. Message’s size is smaller than N sections format and coordinator failure fault tolerance is also considered. The format is based in this paper and is shown in Fig. 3. In each step the processes that receive messages with same label and same initiator from it sides, will kill the message to avoid exchanging waste extra messages. In our algorithm we suppose that the end to end time between each two process is the same, so if the number of process is odd at the end two neighbor processes will send messages to each other simultaneously. Therefore, two processes will receive messages from their two sides at the same time; they make Coordinator or Surrogate Coordinator messages simultaneously (same as each other) and will throw it in the network. But since election result of these two processes are same as each other, throwing Coordinator message in the network isn’t important, therefore, if a process receives two Coordinator or Surrogate coordinator message, it’ll stop one of them.

SCID

Coordinator ID

informer ID

Fig. 3: Three section message format

• V. Proposed Algorithm

Different kind of messages could be passed in a typical system, but four kinds of messages are considered in order to election in our algorithm.

• 1)    Election message : When there is no coordinator in the system, one process such as process 3 in Fig. 4 creates an Election message, and then puts its number in informer section and coordinator message’s

sections, after it puts zero in the surrogate coordinator section, finally it’ll send message to its successor and predecessor.

• 2)    Coordinator message : At least one process such as process 6 in Fig. 5 will receive Election messages (which have the same informer number) from its two sides. This process then works according to following steps:

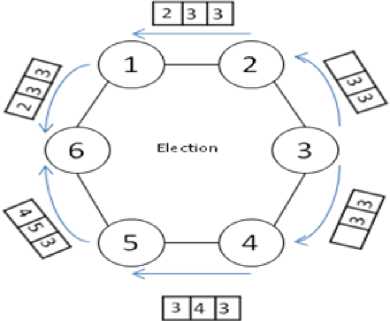
Fig. 4: Process number 3 creates Election message

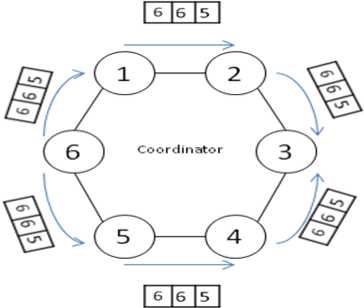
Fig. 5: Coordinator message from process number 6 which delivered election message from its two sides from one starter

• •    First of all it checks that whether these two Election messages have same labels and informer process or not

• •    Then it doesn’t allow the messages to throw again in the network.

• •    Next it compares the two messages coordinators and surrogate coordinator’s number, and then it selects greater ones as coordinator and other as surrogate coordinator.

• •    After, this process creates a message, labels it as Coordinator message, puts its number into informer, elected coordinator section, and into surrogate coordinator section.

• •    Finally new informer (this process) throws this message into the network.

• 3)    SElection message: If processes find coordinator crash out (process number 3 in Fig. 4, they’ll tolerate it by replacing the surrogate coordinator to coordinator. While this process is continuing its ordinary operation without any delay, it creates a message, labels it as SElection and puts the last surrogate coordinator into coordinator section, zero into surrogate coordinator section and its own number into informer. Then the process throws the message into the network. Each process in the network which didn’t notice about coordinator crash, will replaces the surrogate coordinator to coordinator by receiving this message and then it compares its own number with message’s surrogate coordinator to elect new one. After that it’ll pass the message into network in the same direction it received. This scenario is shown in Fig. 6 and Fig. 7.

In each step the processes that receive messages with same label and same initiator from it sides, will kill the message to avoid exchanging waste extra messages. In our algorithm we suppose that the end to end time between each two process is the same, so if the number of process is odd at the end two neighbor processes will send messages to each other simultaneously.

Therefore, two processes will receive messages from their two sides at the same time; they make Coordinator or Surrogate Coordinator messages simultaneously (same as each other) and will throw it in the network. But since election result of these two processes are same as each other, throwing Coordinator message in the network isn’t important, therefore, if a process receives two Coordinator or Surrogate coordinator message, it’ll stop one of them.

• 1)    Scoordinator message : Same as the Coordinator message, at least one process receives message with same label and initiator from its two sides. Then each of these processes will make a SCoordinator message separately.

After electing coordinator and surrogate coordinator they put the appropriate information into the message’s sections and throw it in the network to inform other processes about new surrogate coordinator. This scenario is also shown in Fig 8 which process 5 throws SCoordinator message into the network. As it is obvious in this figure some time it is possible that two or more messages with similar labels and different initiator numbers are passing in network.

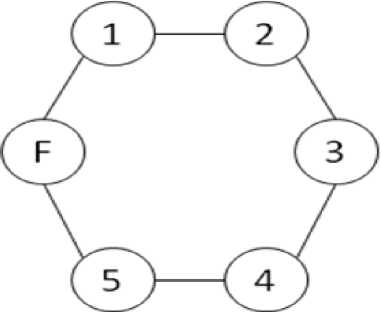
Fig. 6: Coordinator (process number 6) failed

5

5

4

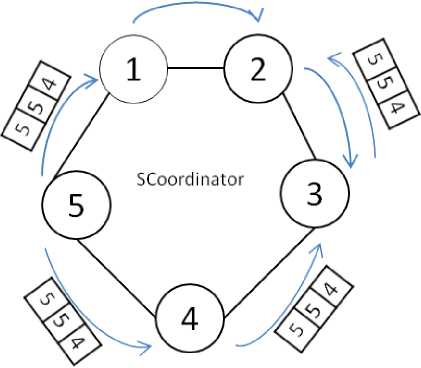
Fig. 8: Process number 5 created Scoordinator message and throught it in the network

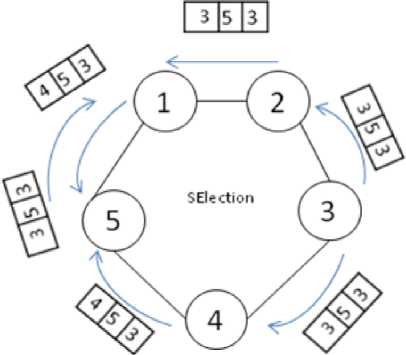
Fig. 7: SElection messages after denying failed node from process number 6

The event happens because more than one process find crash out or Election or SElection message don’t receive to one process at the same time, so two neighbors processes will throw the Coordinator and Scoordinator messages with different initiators and same labels.

The solution for this issue is that each process in the network which receives two messages with identical labels but different initiators will check the initiator numbers and will stop the message with lower initiator in order to alleviate throwing waste extra messages. Our algorithm in each step specified surrogate coordinator and coordinator, so if one process with the larger

number comes into the network before coordinator failure, system will omit it in election until next the next one to avoid 2n message overhead.

The flowchart of the Election and SElection message’s function of a typical process is determined in Fig. 9. In this flowchart first of all processes find out message type by message’s label. As we see, when message type is Election, if process receives another message with the same informer, this process finds out that this message has gone all around the network and it creates new coordinator message. Since we consider a coordinator’s alternative, the number of messages which should be passed into the network in order to inform processes about crash is equal to number of processes.

This is also fewer than the number of messages which passed by basic Ring algorithm. This fact is This fact is illustrated by an example in Fig. 10. As we can see when the number of processes in the particular network is odd, the number of messages which is passed among them to figure out crash and then to elect a new coordinator is n+1, which n is the number of processes. But if number of processes be even, the number of message will be changed to n.

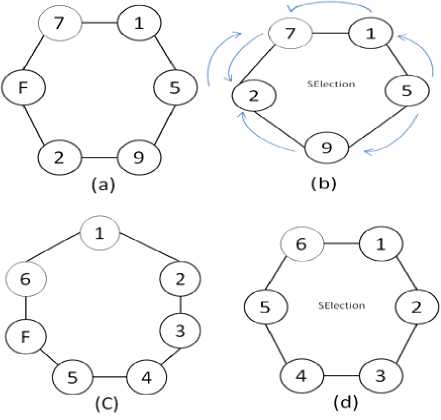
Fig. 10: exchanged message number between processes to find coordinator crash and elect new one

Low message complexity of an algorithm is considered as a great advantage. However if these messages exchanged during long period of time, the algorithm is almost impractical and useless so both of message complexity and time complexity of an algorithm should be analyzed.

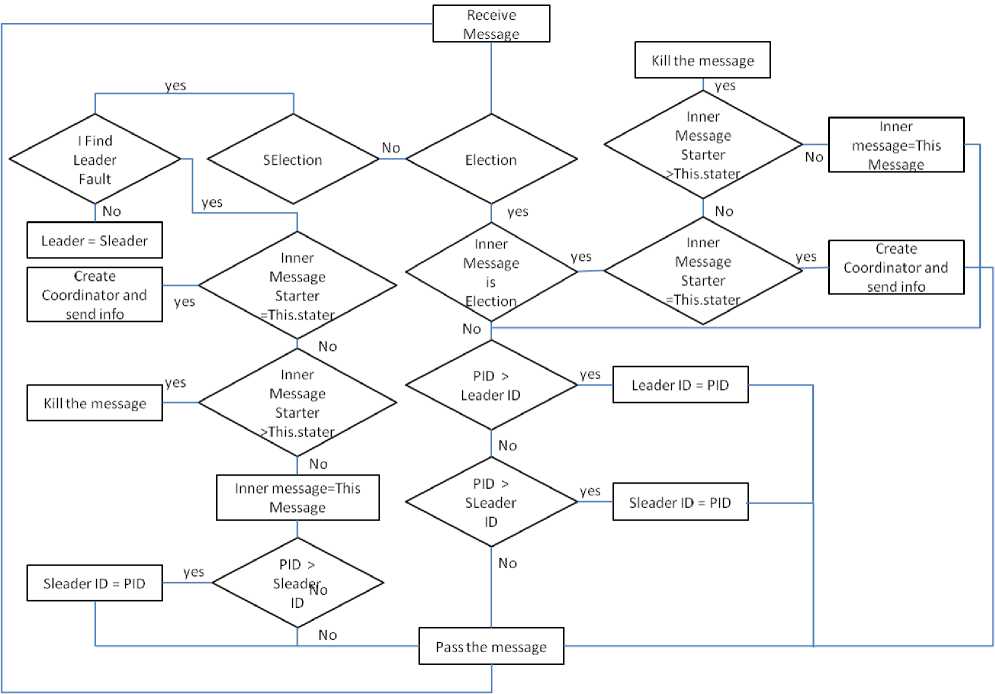
Fig. 9: Election and SElection Operations of typical process

• VI.    Mathematical Analyze

  • 6.1.    Message Complexity Analyzing

• 6.2.    Time Complexity Analyzing

The number of messages which exchanges via this algorithm (MN) depends on the number of processes in the network (N) and number of those which find coordinator crash out (FPN). Therefore MN is calculated by (1) which is from O (N) and Ω (N).

MN=(FPN-1)∗(  )+ 2N           (1)

A mathematical comparison between this algorithm and basic ring is inserted in Table (1). In the rest of the paper we’ll refer to our algorithm as FCEABR (Fault tolerant Coordinator Election algorithm in bidirectional Ring).

During election procedure Election messages are circulated among all the processes in the network, and then they should be informed about elected coordinator and its alternatives. Moreover any process compares its own number with Election message’s coordinator and its alternatives. As discussed before, number of messages passed by this algorithm is variable due to number of processes in the network. Communication time between each two processes (α) is considered to be the same for simplicity so Communication Cost (CC) of the algorithm is gained by (2).

2∗(N-1)∗α

2∗N∗α

N is even

N is odd

Total Processing Time (PT) by processes in the network also calculated by below equation when considered as processing time for comparison between two scalars by a typical process.

Table 1: Mathematical comparison between FCEABR and Ring algorithm

FPN/Algorithm	FCEABR	RING
1	2N	2N
2	2N+N/2	4N
10	2N+ (9/10)*N	10N
.	.	.
.	.	.
.	.	.
N	3N-1	N2

PT=2∗(N-1)∗β(3)

Therefore, (6) calculates Election process Consuming Time ( ЕСТ ).

λ ! =  ∗(2∗(N-1)∗β+(2∗N-2 )∗α)(4)

^2 = ∗(2∗(N-1)∗β+2∗N ∗α(5)

=λ1

ECT={λ    N is odd(6)

However (3) and (6) will be changed to (7) and (10) respectively when all coordinator alternatives are already crashed but coordinator is still up.

PT=(N-1)∗β(7)

λ3 = ∗((N-1)∗β+ 2∗(N-1)∗α)(8)

λ4= ∗((N-1)∗β+ 2∗N∗α)(9)

ECT={λλ3(10)

λ    N is odd

β and α are constant variables, so time complexity of the algorithm is from O (N) and Ω (N).

• VII.    Simulation Result

  The simulation program has written by Microsoft visual studio 2010, C#.Net Programming Language. Random numbers are assigned to each process and processes which find crash out are randomly selected. Therefore number of messages in each test may differ from another same test because of this randomization. Program has run 50 times for the same numbers of processes and average is gained for variables. In simulation procedure we will refer to basic Ring algorithm as Ring. At first FCEABR is compared with basic ring algorithm.

The result of first simulation which network has 35 processes is shown in Fig. 11. It is obvious that FCEABR exchanged fewer message than basic Ring algorithm.70 processes are placed in the second test (Fig. 12). By comparing first test and second one it is concluded that by appreciating the network’s process number and number of processes that find coordinator crash out, FCEABR decreased the number of exchanged message in comparison to basic Ring algorithm.

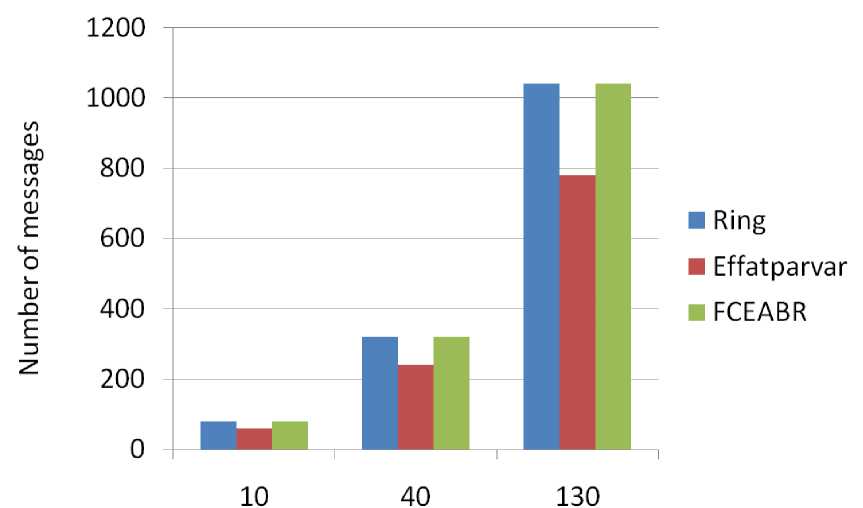
• •    In the rest of this section 3 scenarios are considered and the result of FCEABR algorithm, basic Ring algorithm, and Effatparvar algorithm will be compared..The first ones is the number of messages that passed to inform processes crash.

• •    Second ones is the number of passed message when coordinator crashed and one process finds it out

• •    Third ones is the number of exchanged message when coordinator crashed and three processes find it out.

We show the result of these scenarios in Fig. 11, Fig. 12 and Fig. 13 respectively. In Fig. 10 it is obvious that the number of exchanged message by FCEABR and simple Ring algorithm is similar to each other but it is more than Effatparvar algorithm. This is because of putting out election to the time when coordinator and alterative of coordinator crashed. Our algorithm passed more messages in this case but no wait time is inducted to any processes during their run time because of coordinator crash.

It should be mentioned that tolerating waiting time by processes may cause dangerous problem especially in real time usages.

Fig. 11 shows the second scenario of our simulation and we can see that our algorithm passed fewer and fewer messages in comparison to other algorithms especially when the number of processes which find coordinator crash out is going to be more and more.

This reduction happened because in other algorithm each process that finds coordinator crashed creates Selection message separately and its messages are fully passed among processes but by FCEABR when a new Election message is delivered to the process which received the same message with other informer number before, it’ll compare two Election message’s informer. If the new received ones have lower number, the process will stop it.

We also obtain the number of messages that was passed among processes to inform them about crash for four networks with different number of processes and the result is inserted into Table 2. In this Table, it is obvious that the number of messages exchanged among the processes when coordinator crashed by our algorithm is nearly half fewer a .than basic Ring algorithm. Also, it figures out the differences between odd number of process and even number too.

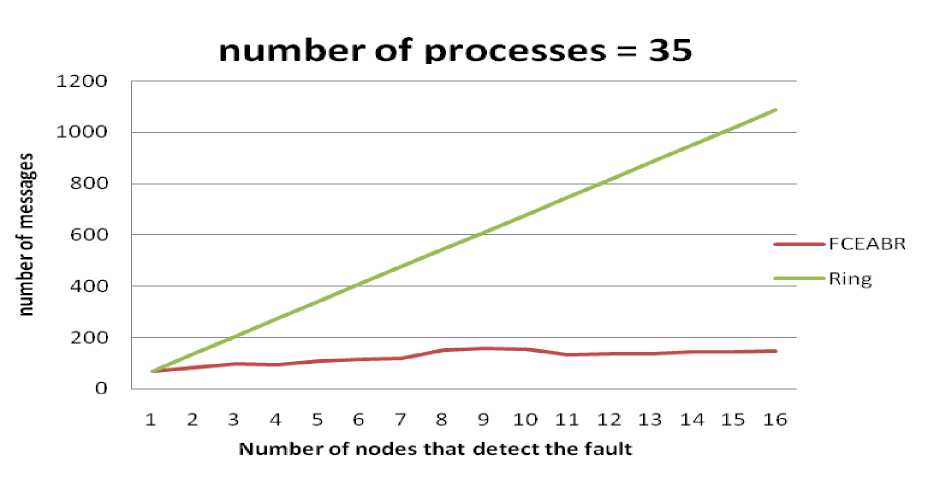
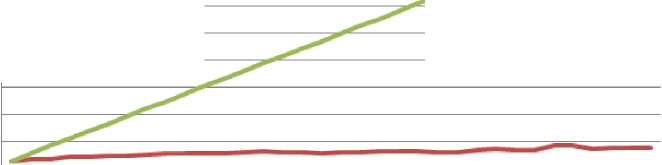
Fig. 11: FCEABR and basic Ring Comparison when number of processes is 35

4500 й 4000 3 3500 | 3000

2500 - 2000 ^ 1500 = 1000

500 0

number of processes = 70

FCEABR

Ring

1 3 5 7 9 11 13 15 17 13 21 23 25 27 29 31 33

Number of nodes that detect the fault

Fig. 12: FCEABR and basic Ring Comparison when number of processes is 70

Number of processes

Fig. 13: Total exchanged message number when coordinator crashed and one process finds it out after four time coordinator crash.

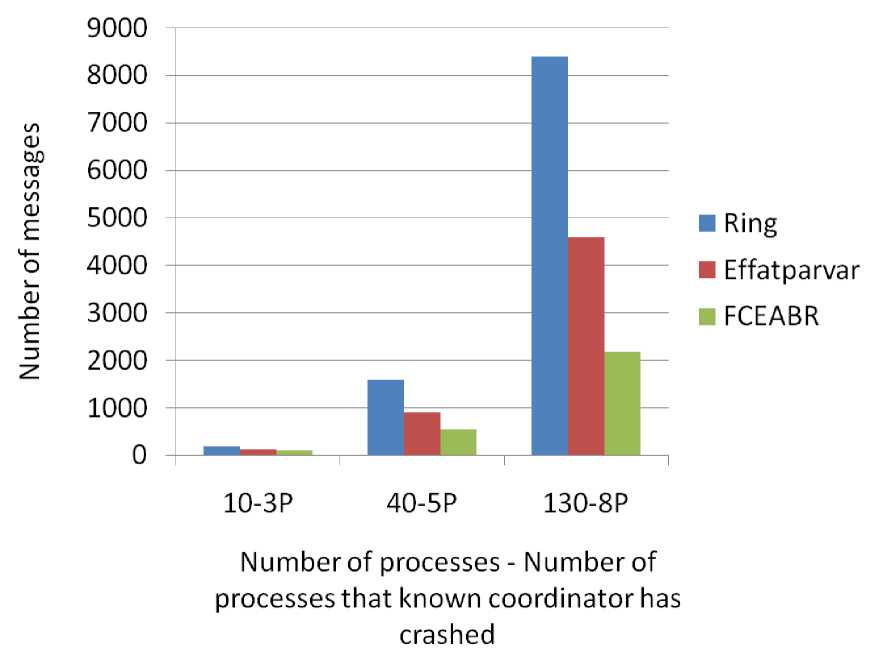
Fig. 14: Total number of messages that passed after four times that coordinator crashed and different number of processes fined this out

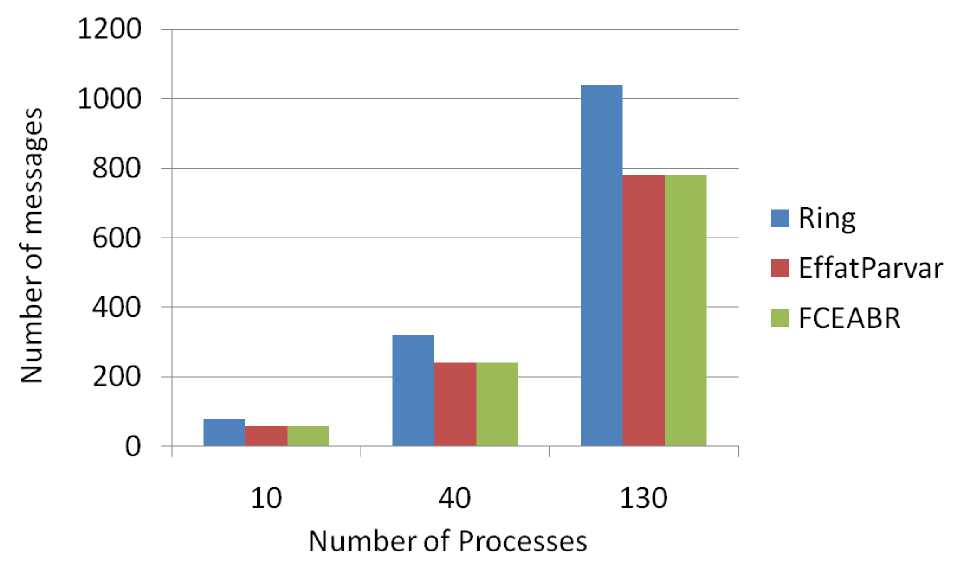
Fig. 15: Message passed to inform processes about crash during four times coordinator crash

• VIII.    Convergence Approving

We select the processes that find coordinator is crashed randomly, so we approve the final result (number of messages passed in network) convergence of our algorithm by calculating its standard deviation. The average number of messages ( X ) that is exchanged during 200 times of test repetition is gained by (11) and due to unknown statistical community, sample variance ( Sx ) that calculated by (12) should be used.

Table 2: Number of messages when coordinator crashed in four networks with different number of processes before coordinator crash (NPBCC)

NPBCC	Modified Ring	Ring
50	98	50
187	372	186
1290	2578	1290
5890	11778	5890

X ∑ = r 2   ∑L( Xi-X)

Therefore standard deviation is calculated by be below equation.

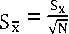
NPS	NOF	ANSRM	SD
40	3	112	0.022
115	6	392	0.011
320	11	1287	0.302
830	20	3820	0.405

We calculate variance and standard deviation for four different networks. The specification of networks and average number of messages that passed after 200 times repeating the test is inserted in Table 2.

In Table 3 different parameters of a network is identified. For example when we run our simulator 200 times for a network with 320 processes which 11 processes finds crash out; the average number of messages passed would be 1287. Also, the standard deviation of the messages is 0.302.

• IX.    Conclusion and Future Work

As we read in previous section, our method to identifying a coordinator was based on bidirectional ring network. We found that our algorithm passed fewer messages than Ring algorithm to elect new coordinator and also it increased the election’s speed. In each step a coordinator and its surrogate coordinator was identified so if a coordinator was failed, each process could continue its functions without waiting which means the process’s waiting time is leaded to zero. Each process could tolerate one failure. Also three sections message format which miniaturizes the size of the message was used. Processes in our algorithm saved the information of coordinator and its alternative in each step which doesn’t consume much memory especially when we have just one alternative. The only operation that was added to election procedure was comparison between numbers in processes and received messages. Control packets could easily pass between processes in the network because the labels of coordinator election algorithm messages made them differ from other types of messages. As the future work we are going to apply this algorithm into multi management sites systems which can share their resources among processes in their sites or even other site’s processes

• [1]    Y.Afek and A. Gafni, “Time and message bounds for election in synchronous and asynchronous complete networks,” in Proc. 4th Annu. ACM Symp. on Principles of Distributed Computing, Minaki, Canada, Aug. 1985, pp. 186-195.

• [2]    R. Gallager, P. Humblet and P. Spira, “A Distributed Algorithm for Minimum Weight Spanning Trees,” In ACM Transactions on Programming Languages and Systems,vol.4, no.1, pages 66-77, January 1983.

• [3]    N. Malpani, J. Welch and N. Vaidya, “Leader Election Algorithms for Mobile Ad Hoc Networks,” In Fourth International Workshop on Discrete Algorithms and Methods for Mobile Computing and Communications, Boston, MA, August 2000

• [4]    P. Basu, N. Khan and T. Little, “A Mobility based metric for clustering in mobile ad hoc networks,” In International Workshop on Wireless Networks and Mobile Computing,, April 2001 Page(s):658 – 663

• [5]    A. Obeidat and V. Gubarev. “Leader Election in peer to peer systems. Siberian conference on control and communications SIBCON-2009.

• [6]    N. Fredrickson and N. Lynch, “Electing a Leader in a Synchronous Ring.” J.ACM, 1987, vol.34, no.1, pp.98-115.

• [7]    H. Garcia Molina, “Elections in a Distributed Computing System. Y. Afek and A. Gafni, “Time and message bounds for election in synchronous and asynchronous complete networks,” in Proc. 4th Annu. ACM” IEEE Trans. Comp, 1982, vol.31, no. 1, pp.48-59.

• [8]    E. Chang and R. Roberts, “An improved algorithm for decentralized extrema finding in circular configurations of processes, ”Communications of the ACM}, pp. 281-283, 22,5, 1979.

• [9]    R. Bakhshi, W. Fokkink, J. Pang, and J. van de Pol. µCRL specification of probabilistic Franklin leader election algorithm.     http://www.few.vu.nl/~

• [10]    R. Bakhshi, W. Fokkink, J. Pang, and J. van de Pol.Leader. Election in Anonymous ring, Franklin Goes probabilistic, http://www.few.vu.nl/~ rbakhshi/ alg/franklin.mcrl

• [11]    L. Higham and S. Myers. Self-stabilizing token circulation on anonymous message passing. In Proc. 2nd Conf. on Principles of Distributed Systems, pages 115– 128z Hermes, 1998.

• [12]    J. Burns and J. Pachl. Uniform self-stabilizing rings. ACM Trans. Program. Lang. Systems, 11(2):330–344, 1989.

• [13]    F. Fich and  C. Johnen. A  space  optimal,

deterministic,   self-stabilizing,   leader  election algorithm for unidirectional rings. In Proc. 15th Conf. on Distribute Computing, volume 2180 of LNCS, pages 224–239. Springer, 2001.  S.-T.

Huang. Leader election in uniform rings. ACM Trans. Program. Lang. Systems, 15(3):563–573, 1993.

Danial Rahdari: received his B.S. in computer engineering from Sistan and Balouchestan University, in 2010 and he is studying computer engineering in M.S. at IAU University. His research interests are in the areas of distributed systems, cloud services, quality of service, load balancing and resource allocations algorithm in cloud computing and ad hoc networks.

Amir Masoud Rahmani: received his B.S. in computer engineering from Amir Kabir University, Tehran, in 1996, the M.S. in computer engineering from Sharif University of technology, Tehran, in 1998 and the PhD degree in computer engineering from IAU

University, Tehran, in 2005. He is associate professor in the Department of Computer Engineering at the IAU University. He is the author/co-author of more than 140 publications in technical journals and conferences. He served on the program committees of several national and international conferences. His research interests are in the areas of distributed systems, ad hoc and sensor wireless networks, scheduling algorithms and evolutionary computing.

hoc networks.

Afsane Arabshahi: received her B.S. in computer engineering from Sistan and Baloochestan university Zahedan, Iran in 2011. His research interests are in the areas of distributed systems, cloud computing and cloud services, quality control, load balancing algorithm in cloud computing and ad