Фазовая модель рассеяния микроволн от слоя с шероховатыми границами

При интерпретации данных дистанционного зондирования космическими интерферометрическими радарами основной информативной характеристикой является интерферометрическая фаза радиолокационного сигнала, рассеянного земной поверхностью. Эта фаза определяется как разность фаз рассеянных сигналов, полученных из данных разновременных одного спутника над одним участком земной поверхности или одновременных космических радарных снимков, полученных тандемом спутников. Существующие модели обратного рассеяния радарного микровол- нового сигнала практически не учитывают зависимость фазы радиолокационного сигнала от физических и геометрических свойств почвенных покровов, в частности, от слоистого строения влажности почвы. Обычно при анализе работы интерферометрических радаров используется следующее выражение для интерферометрической фазы сигнала [1]

^ф = Ф topo + Ф def + Ф atm + ^Ф noise , ⁽¹⁾ где слагаемое ф_1оро возникает вследствие рельефа, компонента ф а^ описывает влияние деформаций земной поверхности за время между пролетами спутника, составляющая ф_ат возникает вследствие неоднородности атмосферы, слагаемое ф_по15е обусловлено шумами приемно-передающего оборудования.

В формуле (1) не учитывается зависимость фазы сигнала от изменения отражательных свойств поверхности, которая может быть обусловлена слоистой структурой влажности почвы, влиянием замерзания верхнего слоя почвы и другими факторами. Между тем, вариации фазы могут существенно уменьшить точность метода дифференциальной интерферометрии, используемой для определения деформаций и подвижек земных покровов и сооружений на них [2]. Ранее в работах [3-6] было показано, что слоистость земных покровов вызывает заметные вариации фазы отраженного сигнала. Фаза зеркально отраженного сигнала важна для бис-татической радиолокации например, для GPS рефлектометрии. Ранее фазовая модель обратного рассеяния, учитывающая фазу рассеянного сигнала была рассмотрена в [7, 8], однако в ней не были учтены все волны, рассеянные неровностями нижней границы слоя.

В данной работе проведено обобщение результатов, ранее полученных в [7, 8]. Цель работы заключается в построении основанной на физических соображениях и методе малых возмущений модели обратного рассеяния от слоистой среды с шероховатыми границами раздела для простого случая двухслойной среды и оценка влияния слоистой структуры среды на фазу рассеянной радарной волны. Двухслойная среда может, например, описывать такие земные покровы, снег на земле, лёд на воде, почва с двухслойным строением, травяной покров на почве.

В первых работах, посвященных влиянию влажности, предполагалось, что изменение влажности однородной почвы может влиять на фазу из-за изменения глубины проникновения и вследствие этого изменения глубины эффективного фазового центра рассеяния. Однако в работах [3, 6] было показано, что изменение влажности влажно-однородной почвы может вызывать только слабые изменения фазы, не превышающие нескольких градусов.

Существует ряд работ, где исследовалось обратное рассеяние от двухслойной среды. Для анализа рассеяния электромагнитных волн использовались различные модели, такие как метод малых возмущений [9], полноволновой метод [10], метод Кирхгофа [11] и метод малых наклонов [12]. Во всех этих работах исследовались только энергетические характеристики рассеянной волны. Только в работе [13] рассматривалось влияние слоистости на фазовую сигнатуру, являющуюся разностью фаз рассеянных волн вертикальной и горизонтальной поляризаций.

Модель обратного рассеяния

Перейдем к построению приближенной модели обратного рассеяния, основанной на наглядных физических предпосылках и позволяющей определить фазу рассеянной волны. На рис. 1 показана геометрия задачи. Из среды 1 на двухслойную среду, состоящую из слоя 2, лежащего на полу-бесконечном слое 3, падает плоская электромагнитная волна E_ = e ik i ( x sm ⁹ - z cos ⁹ ( k 1 _ волновое число в среде 1), которая имеет горизонтальную или вертикальную поляризации. Среды 1, 2, 3 характеризуются, соответственно, диэлектрическими проницаемостями е 1 = 1 и комплексными диэлектрическими проницаемостями £ ₂ = £ ‘ + i £ 2' и £ ₃ = £ 3 + i £ 3' . Поверхности (границы) S ₁₂ и S ₂₃ , разделяющие среды, являются статистически шероховатыми поверхностями с неровностями, описываемыми некоррелированными стационарными случайными функциями z 1 (x,y) и z₂(x,y) со средними значениями < z 1 >  = 0 и < z ₂ >  = - b , среднеквадратичными отклонениями s 1 и s ₂ , радиусами корреляции 1 1 и 1 ₂ . Полагаем, что неровности малы по сравнению с длиной волны, их наклоны невелики и выполняются условия применимости метода малых возмущений ks₁₂ < 0,3, kh2 < 3 [14].

Представим поле обратного рассеяния в виде суммы волн, испытавших различное число актов преломления, рассеяния и отражения. Будем рассматривать только поле с поляризацией, совпадающей с поляризацией падающей волны. На рис. 1 лучи, соответствующие когерентным волнам, испытывающим отражение и преломление на плоских (в среднем) поверхностях, показаны сплошными линиями, а лучи, вдоль которых распространяются некогерентные рассеянные волны, обозначены пунктиром.

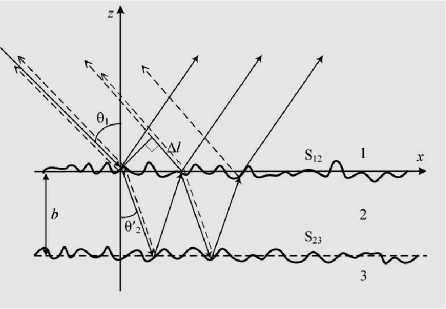
Рис. 1. Геометрия задачи об обратном рассеянии

Коэффициенты отражения и прохождения волн определяются формулами Френеля для плоской границы раздела, т.е. полагаем, что в нулевом приближении неровности не влияют на когерентное поле (борновское приближение) и рассеянное поле, когда оно преломляется по закону 42

Снеллиуса. Поскольку размеры неровностей малы, будем учитывать только однократное рассеяние, поскольку в этом случае влияние эффектов многократного рассеяния между верхней и нижней поверхностью мало. В связи с малостью неровностей также не учитываем изменения фазы волны вследствие влияния этих неровностей. С учетом принятых допущений поле, рассеянное слоем с шероховатыми границами в обратном направлении, можно представить в виде суммы волн

| Ee * = | E 12| + E e ^{- 1} + E 2I e - 2 ,                       (2)

где E ₁₂ – амплитуда рассеянного поля при падении волны E_i на границу S 12 ; второе слагаемое описывает поле, обусловленное рассеянием выходящих после отражений от нижней границы волн на неровностях верхней границы раздела S 12 ; третье слагаемое описывает поле волн, рассеянных на поверхности S 23 . Из выражения (2) следует, что фазы отсчитываются относительно фазы поля E ₁₂ .

Поле E 1 e^i- 1 представим в следующем виде

|E 1 \е‘ ^{ф 1} = T ₁₂ R 23 E 21)| e ^- a ^{+ i ( Ф 1 + ф} ' + T ₁₂( R ₂₃) ² R ₂₁ E 21 ²⁾| e ^{2[ -} a ^{+ i ( Ф 1 +ф} 2 ^)] +

+ t ₁₂( R ₂₃) ³ ( R ₂₁) ² E 21 ³⁾ e ^3[- a ^{+ i ( Ф 1 +ф 2)]} +... t ₁₂( R 23 ) n ( R ₂₁) n ^{- 1} E 21 n ) e n ^{[ -} a ^{+ i ( Ф 1 + ф 2)]} +...

В выражении (3) поле E 1 с амплитудой E ₁ и фазой ψ записано как сумма следующих полей: E ₂ ⁽¹⁾ – поле рассеяния волны в направлении на радар при прохождении через верхнюю границу из слоя 2 в среду 1: (эта волна возникает в результате прохождения через верхнюю границу и слой 2 в прямом направлении, когерентного отражения от нижней границы и падения на верхнюю границу); E ₂ ⁽²⁾ – поле обратного рассеяния волны, полученной в результате четырехкратного прохождения через слой, двукратного отражения от нижней границы, однократного отражения от верхней границы и рассеяния неровностями верхней границы в направлении на радар; и т.д. В формуле (3) через Т 12 и Т 21 обозначены коэффициенты прохождения Френеля через верхнюю границу из среды 1 в среду 2 и, соответственно, наоборот; R 23 и R 12 – коэффициенты отражения Френеля от границ слоя; a – слагаемое в показателе экспоненты, характеризующее ослабление волны при двукратном прохождении слоя; φ 1 – набег фазы волны за счет двукратного прохождения слоя; φ 2 – приращение фазы при распространении в среде 1 на расстояние Δ l .

Параметры a , φ 1 , и φ 2 определяются следующими выражениями:

a = 2k1 b^^2-(71 + tan2 § -1), ф1 = 2k1 b^У2-(71 + tan2 5 +1)^cos92, ф2 = 2btg02 sin 01,                           (4)

„ + . S’          _       kx sin 0         ,     ~ где tan о = —, 02 = a tan----1              , k1 - волновое число в среде

^S 2               Re 4k 22 - ( k ₁ sin 0 1 ) ²

• 1,    k ₂ = k 1 -Js - волновое число в слое 2.

Для поля E ₂ e i ^{2 2} получим

| E 2\ e ² = T ₂ T ₂₁| E 23)| e - a 1 + T ₁₂ R 2₃ R 21 T 2J E g) e ² a ^{+ ф :}" ” ^; + T 12 ( R 2₃ ) ² ( R 21 ) ² T ₂₁| E (3⁾| e ^3(- a ⁺ " ^; ' ² ’ ^; + .. T ₁₂ ( R ₂₃ ) n ^{- 1} ( R ₂₁ ) n ^{- 1} T ₂₁| E 2?| e n ^{( - a} ’ " n ^V " " ² + ...

В выражении (5) слагаемые имеют следующий смысл. Первое слагаемое описывает поле E ₂ ⁽¹ ₃ ⁾ волны, рассеянной неровностями нижней границы S 23 в обратном направлении (эта волна вначале проходит через верхнюю границу и слой 2 в прямом направлении, а затем в обратном направлении); второе слагаемое описывает волну, прошедшую в слой 2, затем отраженную последовательно от нижней и от верхней границ, рассеянную в обратном направлении на неровностях нижней границы (поле E ₂ ⁽ ₃ ²⁾ ) и прошедшую через верхнюю границу в направлении на радар. Следующие рассеянные волны возникают благодаря дальнейшим переотражениям от границ слоя.

Усредняя выражения (2), (3) и (5) по ансамблям случайношероховатых поверхностей S 12 и S 23 , получим

(|E\)e^{i v} = [ E 12I) + ( E J ) e i^{2 1}+( E 2| E ^ ² ,            (6)

(I E J E ^{2 1} = T ₁₂ R ₂₃( E g?| ) e - a ^{+ 1 ( ф | + ф 2)} + T ₁₂ ( R ₂₃ ) ² R ₂₁) E £)| ) e ^{2[ -} a ^{+ ix    ф 2})] +

+ T ₁₂ ( R ₂₃ ) ³ ( R ₂₁ ) ²(| e 23)|) e ³ a ^{+ i Xw+ P 2)]} + ... T ₁₂ ( R ₂₃ ) ⁿ ( R ₂₁ ) ^{n - 1}( E 2 П )|^ e^{n [ -} a ^{+ ixw + ф 2)]} + ...

(I E 2I e ^ ^{2 2} = 7 ^2 T 21( I E 23)! ) e - a ^{+ф 1} + T 12 R 23 R 21 T(|e 222’| ) e²⁽ - a ^{+ 1 ф 1 ) +ф} 2 +

T 12 ( R 23 ) ² ( R 21 ) ² T 21( \E§\) e³⁽- a ^{+ 1 ф з) + 2 ф 2} + .. T 12 ( R 23 ) n ^{- 1} ( R 21 ) n ^{- 1} T 21( \E§\) n (^{n ( -} a ^{+ 1 ф |) + ( n - 1) ф 2} + ...

Поскольку неровности поверхностей     S12  и  S23 являются стационарными случайными функциями, полагаем

• (1)            (2)            (3)(

E 211 = 3 E 211 = 3 E 211 =... = \ E 211 / = \ E 21|/,

• (1)             (2)             (3)(

\|E23 I = \ E23 I = \E23 I = ... = \E23 I = \IE231/ .(1

Используя формулу для бесконечной геометрической прогрессии, получим из (7) – (10)

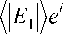
(I E 2 I) _ei ψ 2

TR /I _E |\ - a + i ( ϕ ₁ + ϕ ₂) T 12 R 23 E 21 e

₁ - _{R 23 R 21 e} - a + i ( ϕ 1 + ϕ 2 )  ^,

TT /I E    - a + i ϕ ₁

T 12 T 21 E 23 e

- a + i ( ϕ ₁ + ϕ ₂) ^. 1   R 23 R 21 e

Подставляя выражения (11) и (12) в (6), получим

(I ^E I) _ei ψ =(I E ₁₂ I) ⁺

T 12 ( R 23 (I E ₂₁ I) e^{i ϕ 2} + T ₂₁ (I E ₂₃ I) _{) e} - a + i ϕ ₁

₁ - _{R 23 R 21 e} - a + i ( ϕ 1 + ϕ 2 )

Полагаем, что E_тn l\ ² = С (I E_тn ² ,            тn             тn

где С – константа, m принимает

значения 1, 2, а n – 1, 2, 3. Например, для распределения Релея C = π/4. В 22

свою очередь, значения d E12 I у и d E23 I у по определению пропорцио- нальны соответствующим коэффициентам обратного рассеяния (backscattering coefficient) σ0. При рассеянии волны в результате прохож- дения шероховатой границы раздела для коэффициента рассеяния используется обозначение σt [14]. С учетом этих обстоятельств формула (13) приведётся к виду

0 i ψ 0 σ e ψ = σ ₁₂ +

T ₁₂ ( R ₂₃

t   i ϕ ₂

σ ₂₁ e  + T ₂₁

σ ₂0_{3 ) e} - a + i ϕ 1

₁ - _{R 23 R 21 e} - a + i ( ϕ 1 + ϕ 2 )

где σ0 – результирующий коэффициент обратного рассеяния, σ102 – ко- эффициент обратного рассеяния от верхней поверхности, σ203 – коэффи- циент обратного рассеяния от нижней поверхности, σ2t1 – коэффициент рассеяния волны в направлении на радар при прохождении из среды 2 обратно в среду 1.

Величину σ ⁰ eⁱ ψ назовем комплексным амплитудным коэффициентом обратного рассеяния.

В рамках метода малых возмущений коэффициент обратного рассеяния для волны с волновым числом k, падающей под углом θ на среду с диэлектрической проницаемостью ε и шероховатой границей со среднеквадратичным отклонением неровностей s и радиусом корреляции l , имеет вид [14]:

σ ⁰ = 8 k ⁴ s ² cos⁴ θa _p I ² W (2 k sin θ ,0) .             (15)

В формуле (15) индекс p у параметра αp характеризует поляризацию волны: p = h при горизонтальной поляризации, p = v при вертикальной поляризации. Значения αh и αv определяются соотношениями ah

ε - 1

(cos θ + ε - sin ² θ ) ²

=( - )    (ε-1)sin2θ+ε av = (ε - 1)                         . (16)

( ε cos θ + ε - sin ² θ ) ²

Функция W(2ksin θ,0) является спектром неровностей шероховатой поверхности

∞∞

W ( k x , k y ) = ₂1 π ∫∫ ρ ( u , v )exp( jk _x u + jk _y v ) dudv ,      (17)

-∞-∞ где ρ(u,v) – коэффициент корреляции.

Коэффициенты обратного рассеяния σ102 и σ203 в (7) определяются с помощью формул (6) – (8), с заменой обозначений: для рассеяния верхней границей величины k, s, θ, ε заменяются соответственно на k1, s1, θ1, ε1, а для рассеяния нижней границей на Re(k2), s2, θ2’, ε3/ ε2.

Коэффициент рассеяния σ ₂ ^t ₁ на основе соотношений, приведенных в [12], представим в виде

σ ₂ ^t ₁ = (8 k ₁ Re( k ₂) s ₁ cos θ ₁ cos θ ′ ) ² a ² _p ¹ I ² W ( k ₁sin θ ₁ + Re( k ₂)sin θ ₂ ′ ,0), (18)

где ah21

a v ²¹

(1 / ε ₂ - 1)

1 - sin ² θ ₁ / ε ₂ ) + cos θ ₁/ ε ₂ )(cos θ ₂ + д/ 1/ ε ₂ - sin ² θ ₂ ) ²

(1 / ε ₂ - 1) V (1 - sin ² θ ₁ / ε 2 )(1 / ε ₂ - sin θ ₂ )

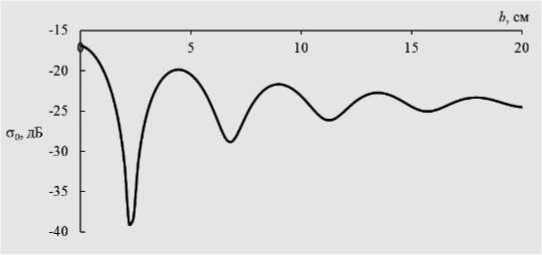
Рис. 2. Зависимость коэффициента обратного рассеяния от толщины слоя

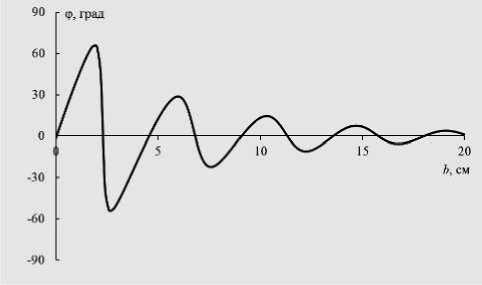
Рис. 3. Зависимости фазы эффективной комплексной амплитуды рассеяния от толщины слоя

Приведённые результаты показывают, что влияние слоистого строения влажности почвы может вызывать значительные изменения, как амплитуды, так и фазы волны обратного рассеяния. Например, изменение фазы, равное 65º и наблюдаемое при толщине слоя 2 см. В радиолокационной интерферометрии изменению фазы на 2π соответствует изменение наклонной дальности на 2/ 2, следовательно, изменению фазы на 65° при 2 = 23 см соответствует невязка 2,1 см. Поскольку для дифференциальной интерферометрии необходима субсантиметровая точность, учет таких невязок необходим. Отметим, что расчетные значения амплитуды и фазы существенным образом зависят от параметров слоя, что обуславливается интерференционной природой результирующего сигнала.

Заключение

На основе метода малых возмущений построена приближенная фазовая модель обратного рассеяния от двухслойной среды с шероховатыми границами. Численные расчеты показали, что слоистость вызывает значительные изменения фазы и амплитуды волны обратного рассеяния, которые необходимо учитывать при обработке данных микроволнового радарного дистанционного зондирования.