Фазовое кодирование при итерационном расчете синтезированных голограмм на компьютере

Для ряда применений лазерной технологии актуальной задачей является создание чисто фазовых голограмм. Первым этапом на пути синтеза голограмм, восстанавливающих изображение путем воздействия только на фазу падающего света, явилось создание киноформа {1}. Процесс синтеза киноформа заключался в том, что по заданному распределению комплексной амплитуды на голографируемом объекте рассчитывались отсчеты фазовой функции математической голограммы и наносились на прозрачную регистрирующую среду в виде разных значений оптической толщины. Восстановление изображения с киноформадает изображение исходного объекта, искаженного из-за пренебрежения амплитудной информацией. Однако энергетическая эффективность восстановления изображения достаточно высока, так как изображение восстанавливается в единственном дифракционном порядке.

В дальнейшем было предложено несколько подходов, позволяющих синтезировать фазовые голограммы с более высокими качественными характеристиками восстановления, чем у киноформа.

П ерейдем к математической формулировке задачи. Пусть исходный объект задается интенсивностью Дх,у) на некоторой двумерной области G. Комплексная амплитуда ч(х,у) определяется амплитудой |w(x,y)|=//(x,y) и некоторой вводимой фазой #(х,у): w(x,y)=|w(x,y)|exp(zXx,y). R - оператор, описывающий распространение световой волны от плоскости регистрации голограммы к плоскости наблюдения. Функцию И^и,г)= R"'(w(x,y)) будем называть математической голограммой объекта, где R - оператор, обратный к R и описывающий переход от плоскости наблюдения к плоскости регистрации голограммы.

Голограмма освещается плоской волной. Необходимо по математической голограмме tP(u,i') построить такую фазовую функцию ИДм.г^СехрОХщт)) (Oconst), чтобы интенсивность восстановленного изображения |w'(x,y)|2, где u'(x,y)= R( И'(м,г)) была близка к интенсивности исходного объекта.

В качестве критериев восстановления выберем относительную среднеквадратичную погрешность восстановления, рассчитываемую по формуле:

ff(l w(x.y) | -1 р w\x,y^ tfdxdy

^Л --------------------,       (1)

Я W,y^dxdy

G где ц - нормирующий множитель, в случае, если исходный объект является бинарным:

I^Uy)^

где |w'(x,y)|cp - среднее значение амплитуды восстановленного изображения объекта, и энергетическую эффективность, определяемую следующим образом:

H\w\x,y^dxdy g                                         (2)

где Е_о - энергия восстанавливающей световой волны. Отметим, что иногда имеет смысл интеграл в числителе формулы (2) брать по некоторому расширению области фокусировки G+^G из-за возникающих погрешностей восстановления.

В [2] был предложен метод кодирования амплитудно-фазовых характеристик функции комплексного пропускания, являющийся обобщением метода Кирха-Джонса. Суть метода в переходе от комплексной функции пропускания И^дл) к фазовой w\u,v) в форме:

И/Ди^ехр^'ф^,!/))

ф ( и, и) = argi IV( и, И)+(—- ] В О (1У^У111

V 2 Г (         /

о

xp(vxU,vyK) , где p^t) - произвольная периодическая функция несущей с периодом 1, принимающая значение р(г)е|-1,1|; фтахе[0,2л-] - максимальный сдвиг фаз; ^€[0,1 ]; QG) - нелинейное предыскажение амплитуды, 0< Q^< 1 при 0<г<1, причем 0(0)= 1, 0(1 )=0; r?=(i?„py) - вспомогательная несущая пространственная частота, выбираемая, исходя из разделения дифракционных порядков. Метод ориентирован навосстановле- ние изображения в нулевом порядке дифракции, а высшие дифракционные порядки являются "платой" за чисто фазовый характер элемента. При синусоидальной несущей Х0=со5(2тг/) и Vy придем к методу Кирха-Джонса. При прямоугольно-импульсной несущей />(г)=1, Kz<0,5+/; /=0,±1,±2,.„ , р^-\, 0,5+/<1+/с ^=( 1/6’, 1/6’), где б1 - шаг дискретизации, мы придем к методу синтетических коэффициентов. В [2| рассмотрен выбор нелинейного предыскажения QU) в зависимости от вида несущей p(t\ В частности, при ,(0=cos(2„) ofW^L/W^l где lV0=max^l/V(u,v)|j, a Jo - функция Бесселя 0-го порядка. При прямоугольно-импульсной несу щей Q(llV(u,u)l)=arccos[1^^^2!

Однако выбор в качестве нормированной амплитуды —!—v   — приводит к низкой тах[ |W(u,v)|]

энергетической эффективности восстановления голограммы, так как в этом случае значительная доля энергии приходится на высшие порядки дифракции. Поэтому рекомендуется выбирать нормированную амплитуду следующим образом:

l^(“,v)|/Hz0, если | И^м,?)^ И^; 1, если | ^(^v^ И70, где

//|И/(и,и)|^и где D - область восстановленного изображения, а |Д| - ее площадь.

Общим недостатком методов кодирования является низкая энергетическая эффективность восстановления, обусловленная возникновением побочных изображений в высших порядках дифракции.

В [ 3] для повышения качества восстанавливаемого изображения было предложено использовать алгоритм Герчберга-Секстона. Алгоритм работает следующим образом: исходное распределение |и(х,у)| дополняется слу-чайной фазой р ( х , у ) : w(x,y)= |м/х,у)|ехр(/Хх,у)); рассчитывается его математическая голограмма И7( и, у)= R"1 (Цх,у)), амплитуда замен я етс я на константу, объект восстанавливается и'(х,у)= R(B'(n,v)) и фаза восстановленного объекта используется в качестве дополнения исходного распределения амплитуд на следующей интеграции.

Использование алгоритма Гечберга-Секстона позволяет рассчитать фазовые голог-раммы, восстанавливающие исходное изображение с меньшей погрешностью, чем киноформ, однако не позволяет полностью избавиться от искажений, вызванных пренебрежением амплитудной информацией.

В данной работе предлагается совместить итерационное восстановление исходного объекта с кодированием амплитудно-фазовых характеристик функции комплексного пропускания в чисто фазовые при синтезе голограмм на компьютере.

Для расчета отсчетов фазовой функции фазовой голограммы предлагается следующий алгоритм:

• 1.    Формирование матрицы отсчетов исходного изображения |w(x,y)|;

• 2.    Формирование матрицы отсчетов случайной функции ^(х,у), равномерно распределенной на отрезке |0,2т|;

• 3.    м<\,у)= |w(x,y) |ехр(/^(.х,у));

• 4.    Дополнение матрицы отсчетов w(x,y) нулями, что физически соответствует выбору частоты несущей;

• 5.    Формирование матрицы отсчетов голограммы исходного объекта HV6v)^R'¹(H’(x,y));

• 6.    Нормировка амплитуд (4);

• 7.    Решение уравнения линеаризации и расчет фазовой функции синтезируемой голограммы ф(//,г) согласно формуле кодирования (3);

• 8.    Формирование матрицы отсчетов функции комплексного пропускания голограммы МДмл’^СехрО^и.у)), причем значение константы С определяется из равенства Нарсе-валя;

• 9.    Моделирование восстановление голограммы w'(x,y)= R( И^ил’));

• 10.    Подсчет энергетической эффективности е (2) и погрешности восстановления б (1);

• 11.    Выбор в качестве ^(u,v) фазы восстановленного объекта и переход к п.З.

В данной работе приводятся результаты численного эксперимента, в ходе которого с помощью предлагаемого алгоритма моделировались синтез и восстановление фазовых голограмм бинарных объектов.

На рис. 1-2 в изолиниях представлены матрицы отсчетов фазовых функций киноформа и голограммы, рассчитанной итерационным метолом синтетических коэффициентов. Отчет-

Рис.1. Изолинии матрицы отсчетов фазовой функции киноформа.

Рис.2. Изолинии матрицы отсчетов фазовой функции голограммы. рассчитанной итерационным методом синтетических коэффициентов.

диво видно результат введения несущей при использовании итерационного метода синтетических коэффициентов. На рис. 3-7 представле- новления изображения с фазовых голограмм.

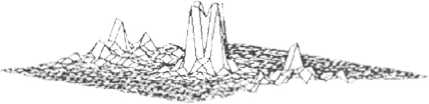
Рис.5. Распределение интспстииности на изображении. восстановленном с голограммы, рассчитанной методом с и птетичес ких ко :ффи цис i гго в.

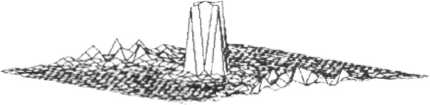
Рис.6. Распределение интенсивности на изображении. восстановленном с голограммы, рассчитанной итерауионным методом синтетических коэффициентов.

рассчитанных методом синтетических коэффи циентов и итерационным методом синтетических коэффициентов. Можно отметить подавление паразитных дифракционных порядков после итерационной обработки. Рис.7 - результат восстановления изображения с голограм мы. рассчитанной методом Герчберга-Секстона.

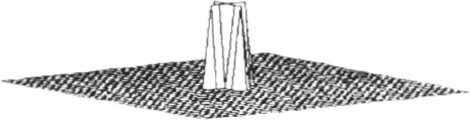
Рис ' Распределение интенсивности на исходном объекте

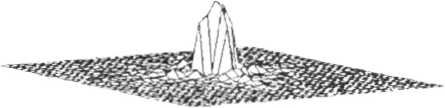
Рис.7. Распределение интенсивности на изображении. восстановленном с голограммы, рассчитанной по методу Герчберга-Секстона.

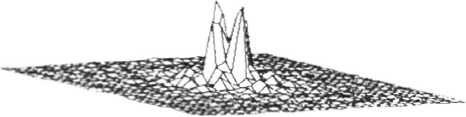
Рис 4 Распределение интенсивности на изображении, восстановленном с киноформа.

ны распределения интенсивностей, полученные при моделировании восстановления изображения крестообразного объекта с фазовых голограмм. рассчитанных различными методами. На рис? - распределение интенсивности на исходном объекте. Рис.4 - результат восстановления изображения с кнноформа; отчетливо видны искажения, вызванные отсутствием амплитудной информации. Рис. 5-6 - результаты восста

В таблицах 1-2 приведены результаты вычислительного эксперимента, в ходе которого моделировалось восстановление изображении с фазовых голограмм, рассчитанных различными методами.

Как видно из приведенных результатов, наибольшую энергетическую эффективность восстановления для данного типа объектов можно получить, используя метод Герчберга-Секстона. Являясь начальным приближением для алгоритма Герчберга-Секстона. киноформ восстанавливает изображение с большими потерями, однако синтез киноформа истребует сложных итерационных вычислении. Применение итерационной обработки в алгоритме Герчберга-Секстона не позволяет полностью избавиться от потерь, связанных с заменой реального распределения амплитуды в плоское -

Таблица I. Результаты компьютерного моделирования восстановления изображения объекта в виде буквы "П".

Используемый метод	Энергетическая эффективность, е	Относительная среднеквадратическая погрешность, <5
Киноформ	0,74	6,19
Метод Кирха-Джонса	0,55	0,14
Метод синтетических коэффициентов	0,52	0,13
Итерационный метод Кирха-Джонса	0,68	0,04
Итерационный метод синтетических коэффициентов	0,69	0,05
Метод I ерчберга-Секстона	0,83	0,12

Таблица 2. Результаты компьютерного моделирования восстановления изображения крестообразного объекта.

Используемый метод Энергетическая эффективность, е Относительная среднеквадратическая погрешность, 6 Киноформ 0,75 0,20 Метод Кирха-Джонса 0,55 0,16 Метод синтетических коэффициентов 0,55 0,12 Итерационный метод Кирха-Джонса 0,70 0,05 Итерационный метод синтетических коэффициентов 0,68 0,05 Метод Герчберга-Секстона 0,88 0,13 ти регистрации голограммы на константу. Методы синтеза чисто фазовых голограмм, использующие для расчета фазовой функции формулу кодирования (3), позволяют уменьшить погрешность восстановления голограммы по сравнению с киноформом. Некоторое снижение энергетической эффективности при этом объясняется появлением побочных изображений в высших порядках дифракции. Сочетание фазового кодирования амплитуды с последующей итерационной обработкой исключает потери, связанные с потерей амплитудной информации, с другой стороны, позволяет повысить энергетическую эффективность восстановления за счет уменьшения энергии высших порядков дифракции. На рис.8-9 изображены графики изменения значений энергетической эффективности и относительной среднеквадратичной погрешности восстановления крестообразного объекта от итерации к итерации для метода Герчберга-Секстона (сплошная линия) и итерационного метода синтетических коэффициентов (пунктирная линия).

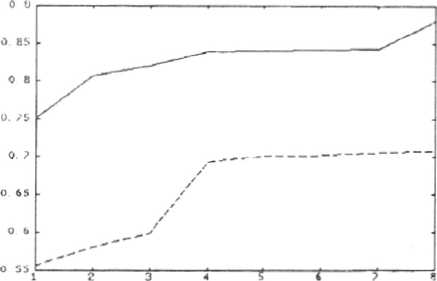
Рис.8. Изменение энергетической эффективности восстановления изображения методом Герчберга-Секстона (----) и итерационным методом синтетических коэффициентов (---) от итерации к итера ции.

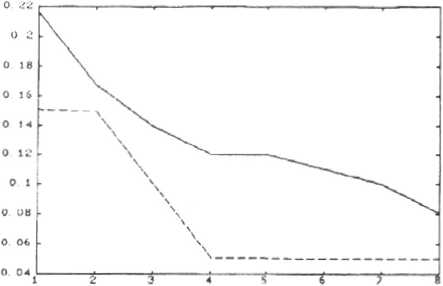
Рис.9. Изменение среднеквадратичной погрешности восстановления изображения методом Герчберга-Секстона (——) и итерационным методом синтетических коэффициентов (---) от итерации к итера ции.

Таким образом, итерационные методы кодирования, сочетающие итерационный расчет фазовой функции с фазовым кодированием амплитуды математической голограммы позволяют синтезировать голограммы, восстанавливающие изображение с довольно высокой энергетической эффективностью при погрешности восстановления намного меньшей, чем может обеспечить алгоритм Гечберга-Секстона.