Фазовые дифракционные элементы для реализации интегральных преобразований пучка излучений

Значительную перспективу для реализации интегральных преобразований излучения имеет предложенная в [10, 11, 15] фазовая дифракционная структура, состоящая из двух разнородных участков, имеющих различные значения отношения ширин dj, d2 прямоугольных канавок к периоду Т их расположения, удовлетворяющие дискретному множеству значений.

В настоящей работе с использованием соотношений Фурье-оптики показано формирование Гильберт-образа пучка в заданном дифракционном порядке указанной фазовой структуры. Достигнуто расширение, по сравнению с [10, 11], множества значений dt /Т, d2/T, при которых наблюдается выполнение преобразования Гильберта. Обоснована возможность реализации Фуко-образа пучка фазовой структурой, участки которой имеют различную глубину фазовой модуляции. Описан эффект безлинзового отображения Гильберт, Фурье и Фуко-образов в изображениях Френеля фазовых решеток, у которых поперечные размеры прямоугольных канавок участков выбраны сравнимыми с периодом Т. При описании использовалось эквивалентное представление гребенки Дирака в виде ряда экспонент с квадратичной фазой. Определены условия реализации семейства интегральных преобразований излучения в дискретном множестве плоскостей наблюдения. Геометрии исследуемых дифракционных структур показаны на рис. 1.

Представим комплексную амплитуду отражения структуры, изображенной на рис. 1а в виде

R(x) = 0,5 (А.-А,) [1 + sign (х)] S 5(х-пТ)®х 1   1п=-”

х reel {-7—) + 0,5 (А. -1) [1-sign (х)] 5 6(х - nT) ® х rect (-7-) +0,5 А, [1+ sign (х)]+0,5[1 - sign(х)],(1)

п=-“ где ® - операция одномерной свертки, А] = ехр (2 ikh2), А2 = ехр (2 ik A h), Ah = 1^ - hj.

При нормальном падении пучка с функцией амплитудно-фазового распределения U (х) комплексная ампли туда дифрагированного поля в зоне Фраунгофера запишется следующим образом

U(x,Z) = -^^ [(А₂+ 1)0(w) + (A₂ - l)U(w)® х

,                ”   1        nnd, а х sign (ы) + (А1 - A^Z*, япТ sin (—у2-) [U (шп) +

+ Н (wn)l + (А, - 1) Z^ -^Т" sin <---Г-) х 1$ "" ™ ^п^}"                                   <2>

Здесь х-координата в плоскости наблюдения, z-расстояние от дифракционной структуры до плоскости наблюдения, знак уголок над функциями обозначает преобразование Фурье-функций, стоящих под этим знаком, по частоте х               ехр [ik (-----+ Z)2]

ы = ----, С(х, Z) = -------- ^XZ ----------, свертка U (w_n)®sigh (n) = H(w_n) представляет по определе-

XZ                Vi X 2

нию [7] преобразование Гильберта от Фурье-образа U (х), X — длина волны излучения.

Для Ah = 0, Х/2 выражение (2) преобразуется к виду

—        ~ г          00     1d. d,

U (x.Z) = С (x.Z) {(А, - 1) Z —7— [С, (n, ~Н 7?-) х

L 1     п=-°° яп 1 Т Т х U(wn) + C2(n, -i-, у?-) Н (w„)] +U(w)},(3)

где

_ / ^dL ^d2 \    - - "•”(d₂ +dj) ,     , я n (d, - d,)

Ct (n, y2-, -^-) = sin (-----2T 1   ] cos [),

C2 (n.

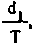
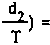
sin

я n (d, - d,) , ------6----^ cos

2T

r                ^dl) ]

2T

В случае, когда отношения d^T и d2/T удовлетворяют следующему дискретному множеству значений d, 2(k'-k")-l

Т ~ 2q где q = 2, 3, 4, .... q - номер дифракционного порядка, в котором осуществляется преобразование Гильберта, к' и к" — целые числа такие, что

0< 2(к'-к")-1 < _{1и 0<} 2(к: + к").±1

2q2q запишем U (x.Z) следующим выражением г 1 л                  1d.

d, а

^-)U(wn) +

U (x.Z) = С(х, Z)(A,

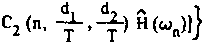
-^^"'"^‘Ji,— К.М

C(x,Z)U(w)

+2

где Oj = q + 2qk,k — целое число.

Наличие первой суммы в выражении (6) доказывает возможность осуществления в порядках с номером П] преобразования Гильберта от U (ш). Порядки с номером n = 2q + 2qk в дифракционном изображении зоны Фраунгофера исчезают. Наряду с этим существуют порядки, для которых С₂ (n₂, dj/T, d₂/T) = 0, а С] (п^.й^П, ^IT) отлично от нуля. В этих порядках формируется U (ш).

При h_t/X= l/8,h₂/X= 3/8 и значениях d^T, d₂/T, удовлетворяющих (4), (5), выражение (3) примет вид f Н (w) 1а а          1        d. d,

U(x,Z)= C(x,Z) [-у- + Z — [U^)- i H («П1)1 +Д— |C2 (n.^, x

A        A              d d- A        A 1

x [U(con)-iH(Wn)]+C,(n.^, ^-)x [H(wn)-iU(wn)l]}.

В (7) выражение U (шп) - 1Й (ып) представляет согласно [7] преобразование Фуко от U (ы). В нулевом порядке осуществляется преобразование Гильберта от Фурье-образа падающего пучка.

Необходимость использования в описанных дифракционных элементах дополнительной фокусирующей оптики для наблюдения картины дифракции Фраунгофера затрудняет их использование для формирования интегральных образов пучков большого диаметра и высокой интенсивности. Для этих целей более перспективно применение дифракционных элементов, позволяющих устранить фокусирующую оптику при выполнении преобразований пучка. В настоящее время в [2—4, 16, 17] решена задача безлинзового формирования Фурье-образа в изображениях Френеля периодической дифракционной решетки. Однако безлинзовые преобразования Гильберта, Фуко оставались нереализованными вплоть до появления работ [12—15, 18-20], в которых обнаружен эффект отображения Гильберт и Фуко-образов в дискретном множестве плоскостей наблюдения промежуточной зоны дифракции. При этом в качестве дифракционной структуры в [15, 19, 20] используется редкая периодическая решетка, позволяющая устранить влияние смещения оси пучка относительно ее центра на формирование изображения Гильберта. Однако применение периодической решетки ограничено сравнительно узким классом функций амплитудно-фазового распределения пучка излучения. Отмеченный недостаток устраняется при помощи решетки [12, 18], состоящей из двух разнородных участков, имеющих значения dp d2 согласно (4), (5), сравнимые с периодом Т. Приведенное в [18] доказательство безлинзового формирования Гильберт-образа ограничено численным экспериментом и не дает полного представления об указанном эффекте.

Выполним аналитическое описание эффекта безлинзового отображения Гильберт, Фуко и Фурье-образов пучка в изображениях Френеля. С этой целью используя фильтрующие свойства 5-функции [21], представим гребенку Дирака для Z, определенных из следующего соотношения*

Z = -^-(8)

рХ в виде о»              -ikx2 m ”    ___2 -in^p

2 5 (х - nT) = ехр (———)2 2 (-l)Pmn х ехр(-----1—) 5 (х - mnT - v Т),(9)

n=-oo                    2Z r-1 п=-°оm где рг = £m/2 - [1 -(-1)]/4-г}.

В результате выполнения преобразования Фурье тождества (9) при соблюдении условий

-Ц- < 1,(Ю)

ml х > NT + Ду.(11)

где N - число периодов в пределах участка дифракционной структуры, получим следующее приближение m «о 2ninv          nd,n

2 X exp (------‘—J sine (----?-) 5 (co—) =

r* i ni-* m          mlm T

• /--- -iff m «о                 nd.          -iff(pp+ n)² ik -_ nT

= VXZ exp(—)2 2 (-l)Pm" sine(—Hxexp [---------] exp[— (x--)].(12)

4 r=i n—”           mT           mp          2Z p

С учетом (12) при выполнении условий (10), (11) запишем комплексную амплитуду поля, дифрагированного на редкой фазовой структуре, отношения d^mT, d2/mT которой удовлетворяют определенному согласно (4), (5) множеству значений в дискретном наборе плоскостей наблюдения (8), в виде

U (x,Z) = 0,5 С (х, Z) {ViXZ (А2 + 1) U (со)® ехр (———) + ViXZ (А2 -1) Цы)® sigh (со)® ехр (у* )* L                             X ZX m 00                 я n (L а аm

+ (А. -А₇) 2 2 С (п, т, р, г) sin (---— ) х [U (о) + iH (gd)] + (А. -1) Z Z C (n, m, p, г) x

• ^{1    z}_r= 1 n=-°°                    m T             ^{n          n 1}_r= i n=-°°

X sin (-^-) [U (щп) - i Й (wn)]}.(13)

„               .       1 )”*n^ P X2 Z2       , -iff^p + n)2n

Здесь C(n,m,p,r) = -—----------- exp [--------[--------], co = (co).

ffn                   m p         nmT

При h = 0,X/2 выражение (13) преобразуется следующим образом и (x,Z) = С (x,Z) (/iTz U (ш)® ехр (---—---) + (А. -1) 2 [2 С (п., т, р, г) Н (со ) +

• 1    г-1 п. 1П

♦ z с («,.„.,. о 0 ^ . z с(п, „. р, „ , к, (n i, А, О („,). с2 ^ ^ А> н к» 1}.о.)

У казанные Z определяют местоположение плоскостей наблюдения изображений Френеля [3].

Из (14) следует, что в полосах с номером nj = mq + 2mqk вблизи координат X] = П] mT/р наблюдается формирование Гильберт-образа пучка. Вторая сумма в (14) описывает при C2(n2, d]/T, d2/T) = 0, a C/n2, d,/T, d2/T)* * 0 отображение Фурье-образа падающего излучения, что расширяет приведенный в [2, 3, 16, 17] класс дифракционных структур для безлинзовой реализации преобразования Фурье. В остальных полосах распределение комплексной амплитуды дифрагированного поля совпадает с преобразованием Фуко-Гильберта.

В случае выбора h^X = 1/8, h2/X = 3/8 выражение (13) записывается в виде

U (x,Z) = С (x,Z){ViXZ 0 (w)® sign (ш)® exp (-^у—) + m                  л        a        m                        d, d, л

+ 2 2 C(n.,m,p,r) [U(w ) - i H (w )] + 2 S C (n, m, p, r) [C. (n, —L.-^-) [H (w ) - r=l "!                   n        n Г=1П^П]              i mT mT n a               d. d, a        a i

-iU(wn)] +C2(n,-L.-4) [U(%)-iH(wn)]]}.                                          (15)

Из (15) видно, что вблизи координат с номером nf отображается Фуко-образ функции U (%)•

Так как при |q| > 10 коэффициент Cj в выражениях (6), (7), (14), (15) практически равен нулю при п не равном, но близком Пр то Гильберт и Фуко-образы наблюдаются в нескольких, рядом расположенных дифракционных порядках (полосах). Число таких порядков (полос) увеличивается с ростом q, зависит от уровня кривизны волнового фронта и может служить его мерой [И, 18].

Анализ дифракционных изображений показал, что описанные интегральные преобразования когерентного излучения сохраняются в рассеянном поле при падении пучка на структуру, изображенную на рис. 16. Отличие в характере выполняемых преобразований наблюдается только в нулевом порядке зоны Фраунгофера, или в пределах проекции падающего пучка на выбранную плоскость наблюдения изображения Френеля.

На рис. 2, 3, 4 приведены численные результаты, позволяющие провести сравнение относительного углового распределения интенсивности в дифракционных полосах, образующихся на расстоянии, задаваемом (8) при р = 1, m = 1, с аналогичными распределениями Гильберт, Фуко и Фурье-образов, полученных при падении пучков с функ циями амплитудного распределения видов

U (х) = ехр [—9 (х/а)],

U (х) = sin (2 k х/а),

U (х) = reel (х/а),

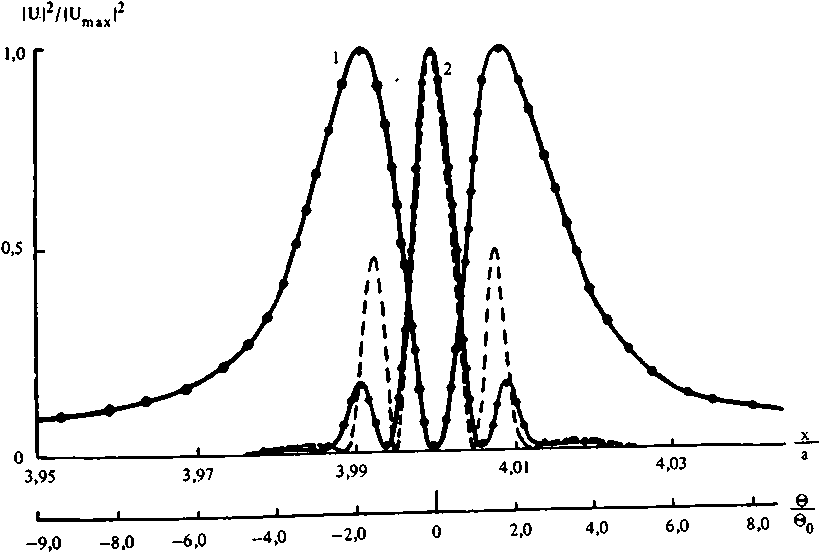
Рис. 2. Относительные распределения интенсивности излучения: N = 20, q = 30, hj/X = h2/X = 0,25, 1 — пучок (16), 2 —пучок (17)

где a = 2 NT - характерный размер пучка. Сплошной кривой на рис. 2 показано относительное распределение интенсивности в дифракционной полосе зоны Френеля. Точки соответствуют дифракционному порядку структуры с "нормальным” сбоем периода [7, 8], выполняющей в зоне Фраунгофера преобразование Гильберта пучка вида U (ы). Для сравнения с соответствующим распределением Гильберт-образа при дифракционной полосе зоны Френеля приведена угловая координата в/ вд. где 0g = X/(2NT), 6 = x/Z. Из графиков видно, что в угловом распределении интенсивности полосы Френеля, номер которой совпадает с определенным согласно (14) значением п,, формируется Гильберт-образ пучка. В плоскостях наблюдения согласно (8) Гильберт-полосы расположены с периодом Т/р, причем при р* 1 происходит их мультиплицирование с коэффициентом, равным р.

При численном исследовании распределения интенсивности поля в изображениях Френеля обнаружено, что для n3 = 2qm + 2qmk функция, модулирующая комплексную амплитуду дифракционных полос имеет минимум, а в полосах с номером, близким к rig, выполняется интегральное преобразование, которое приближенно можно классифицировать как Н (wn).

Пример формирования в полосе с номером ng, равным 37, изображения, близкого к Н(ып) в случае падения пучка (17) на дифракционную структуру, у которой dj/T = 0,975, d^T = 0,925, N = 20, показан на рис. 2 пунктирной кривой. Отличие крыльев данного углового распределения от Й(а>п) обусловлено наложением картин Гильберт и Фурье-образов. Характер искажений H(wn) в указанных полосах зависит от U(x).

Пример безлинзового отображения Фурье-образа в изображении Френеля описанной дифракционной структуры при ДН = 0 показан на рис. 3. Видно, что угловые распределения интенсивности в полосе Френеля и в диаграмме направленности пучка в дальней зоне совпадают.

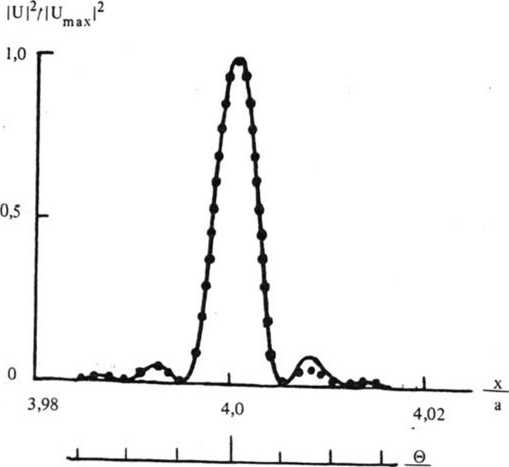
3    -2 -1    0     1      2 з ®п

Рис. 3. Сравнение относительного углового распределения интенсивности в полосе Френеля (------) при

N = 20, q = 20,1ц/X = h2/X = 0,25 с диаграммой направленности пучка (18) в дальней зоне (------)

Возможность отображения Фуко-образа в промежуточной зоне дифракции иллюстрируется графиком на рис. 4. Точками показано относительное угловое распределение интенсивности Фуко-образа, реализованного во втором дифракционном порядке структурой с "аномальным" сбоем периода расположения прямоугольных канавок [12, 13]. Из данного рисунка следует, что при выбранных значениях dj/T, d2/T относительное угловое распределение интенсивности в полосе Френеля совпадает с распределением в изображении Фуко в дальней зоне как в случае пучков (16), (18), так и более сложного пучка вида (17).

Описанный эффект дифракционной структуры - производить безлинзовую реализацию преобразований Гильберта, Фуко, Фурье, Фуко-Гильберта в зоне Френеля - позволяет, выбрав плоскость, расположенную на расстоянии от структуры в соответствии с выражением (8) и измерив распределение интенсивности в дифракционных полосах, выполнить визуализацию фазового объекта, определить диаграмму направленности исследуемого пучка в зоне

IU|2/|Umaxl2

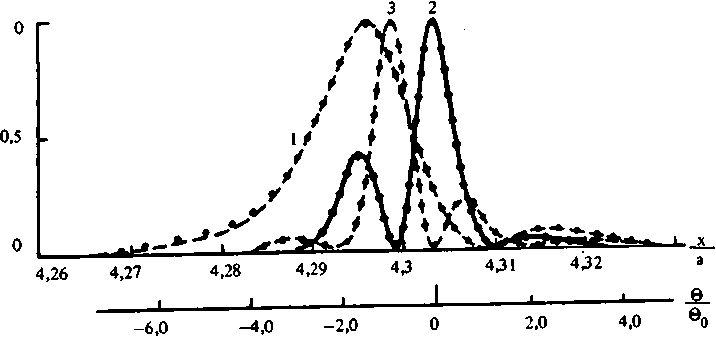
Рис. 4. Безлинзовая реализация преобразования Фуко пучка излучения в полосе Френеля: N - 20, q = 35, hj/X = 1/8, h2/X = 3/8, 1 - пучок (16), 2 - пучок (17), 3 - пучок (18)

Фраунгофера. В результате появляется возможность упрощения существующих схем теневых приборов для диагностики фазовых неоднородностей путем совмещения в одном дифракционном элементе функций фильтров Гильберта, Фуко, Фуко-Гильберта и линзы. Исключение из данных схем фокусирующей оптики расширяет диапазон их применения в сторону больших размеров фазовых объектов и плотностей мощности зондирующих пучков излучения.