Feature Selection based on Hybrid Binary Cuckoo Search and Rough Set Theory in Classification for Nominal Datasets

Published Online April 2017 in MECS

The rapid growth of the number of features in structured datasets in classification causes a major problem, known as “curse of dimensionality”, that reduces the classification accuracy, increases the classification model complexity and increases the computational time, thus the need for Feature Selection (FS) [1] [2]. Koller and Sahami [3] define FS as selecting "a subset of features for improving the classification performance or reducing the complexity of the model without significantly decreasing the classification accuracy of the classifier built using only the selected features ".

Good FS approaches are capable of minimizing the number of selected features without significantly reducing the classification accuracy of all features [1] [4]. In general, the search strategy, which is used to select the candidate feature subsets, and the objective function, which is used to evaluate these candidate subsets, are the two main steps employed in any FS approach [1] [5].

Based on the objective function, existing FS approaches are categorized into two categories: filter approaches and wrapper approaches [1] [6][60]. Filter approaches select the feature subset independently from the classification algorithms using statistical characteristics, such as dependency degree [7] and information measurement [8] of the data to evaluate features of a subset [6][58]. But the wrapper approaches include a classification algorithm as part of the objective function to evaluate the selected feature subsets [2]. Filter approaches are often recognized as faster and more generic than wrapper approaches [2] [6].

The RST approach, proposed in the early 1980s, is one of the effective approaches to feature selection [9] [10] [11]. Its main concept is to search or generate all possible feature subsets and select the one with maximum dependency and a minimum number of features. However, its search strategy (complete search) is very expensive [10]. Several researchers have shown that meta-heuristic algorithms are more efficient for searching [12]. They have been shown to provide an efficient solution for an optimization problem. FS is effectively an optimization problem, since it needs less number of assumptions to find the near optimal feature subset [2] [5] [12]. Thus, many approaches combine meta-heuristic algorithms and RST to solve the FS with higher accuracy and lesser cost.

NIAs are an efficient type of meta-heuristic algorithms [13]. They process multiple candidate solutions concurrently, and they are developed based on characteristics of biological systems [13]. They are widely used for improving the search strategy in FS, because they are easy to implement and incorporate mechanisms to avoid getting trapped in local optima [54] [59][61][65]. These algorithms are also able to find best/optimal solution in a reasonable time with efficient convergence [13][14][65]. Ant Colony Optimization (ACO) [15], Particle Swarm Optimization (PSO) [16], Genetic algorithm (GA) [17], Artificial Bee Colony (ABC) [18], and Cuckoo Search (CS) are known examples of NIAs [65]. Binary CS (BCS) is a binary version of the CS, in which the search space is modelled as a binary string [19].

The ACO algorithm uses graph representation and needs more parameters than others, which makes it much more complex and more expensive compared to other NIAs [20] [16] [15] [18]. PSO, ABC, and BCS use binary representation, which makes their implementation easier and less expensive. The convergence of ABC and BCS is more efficient compared to ACO and PSO because ABC and BCS use a hybrid search mechanism. But BCS is easy to implement and has a more efficient convergence compared to ABC, it uses lesser number of parameters in its local search which makes it one of the fastest algorithms [14] [21][65].

There are several studies in filter FS for classification that combine NIA with Rough Set Theory Dependency Degree (RSTDD). [22] [23] [24][63] employ ACO with RSTDD, [25] [26] [27][62] combine PSO and RSTDD, while [28] [29] [30] [64] use ABC and RSTDD. But according to our knowledge, none of the existing FS approaches use BCS [19] [31] [32][55][56] and RSTDD. Thus this paper proposes a new classification filter FS approach for nominal datasets that combines between BCS and RSTDD. It minimizes the number of selected features (i.e. achieve significant Size Reduction % (SR %)) without significantly reducing the classification accuracy. This approach has developed an algorithm referred to as Feature Selection based on hybrid Binary Cuckoo Search and rough set theory in classification for nominal datasets (FS-BCS).

The remainder of this paper is organized as follows. Section 2 describes RST, CS and BCS. In section 3, details the proposed algorithm FS-BCS. The followed evaluation methodology is described in section 4. Section 5 presents the results and discussion. The conclusion is discussed in section 6. The last section presents the made assumptions and future work.

• II.    RST and Binary Cuckoo Search

RST and binary cuckoo search are the key concepts that our approach bases itself on, these are described briefly below.

• A.    Rough Set Theory

  RST was developed, by Z Pawlak, in the early 1982s [9] as a mathematical tool that deals with classificatory analysis of data table. The advantages of RST are as follows [33] [11]: First, it provides efficient methods for finding hidden patterns in data. Second, it allows to reduce original data without additional information about data. Third, it is easy to understand. Fourth, it allows to evaluate the significance of data using data alone.

RSTDD and positive region are two important issues in data analysis to discover the dependency between the feature subsets and class labels. Positive region (POSp(Q)) contains all objects that can be classified into classes of Q using information in P. The RSTDD can be defined in equation (1) [10] [33] [34].

Y p =

| pos_p ( Q ) | | U |

Where |U| is the total number of objects, |POSp(Q)| is the number of objects in a positive region, and yp (Q) is the dependency between feature subset p and classes Q.

• B.    The Principle of Cuckoo Search

  CS is a new and powerful NIA algorithm that was developed by Yang and Deb in 2009 [20]. CS is a search algorithm inspired by the breeding behavior of cuckoos and L’evy flight behavior of some birds and fruit flies which is a special case of random walks [20] [19] [35]. The reproduction strategy for Cuckoo is aggressive. Cuckoos use the nests of other host birds to lay their eggs in and rely on these birds for hosting the egg. Sometimes, the other host birds discover these strange eggs and they either throw these strange eggs or abandon their nest and build a new one. Cuckoos lay eggs that look like the pattern and color of the native eggs to reduce the probability of discovering them. If the egg of the cuckoo hatches first, it gets all the food that is provided by its host bird [20] [36].

Algorithmically, each nest represents a solution, CS aims to replace the "not so good" solution (nest) with a new one that is better. CS starts to generate the population of nests randomly, then in each iteration, CS uses hybrid search to update the population of nests as follows: The nests that have the lowest quality are updated randomly (global search) [20] [36]. And the remaining nests are updated using local search that uses L’evy flight via the equation (2) and equation (3) [19]:

x t ⁺ 1 = x t + a О L ’ evy ( 2 ) . (2)

Where x^t+1 is a new candidate solution (nest), α is the step size (α>0) scaling factor of the problem, in most cases, we can use α=1. ʘ Means entry-wise multiplications, and λ: L’evy distribution coefficient (0 < λ ≤ 3). Random step length (L’evy (λ)) is calculated from power low by equation (3):

L ’evy uu = s "x . (3)

Where s is step size. L'evy flight is a semi-random search that moves in search space in diverse step lengths depending on the current location to find a good location. L'evy flight makes the CS more efficient in exploring the search space.

• C.    Binary Cuckoo Search

  BCS is proposed by [19] in 2013. It is a binary version of the CS, in which the search space is modelled as a

Classification for Nominal Datasets binary n-bit string, where n is the number of features [19]. BCS represents each nest as a binary vector, where each 1 corresponds to a selected feature and 0 otherwise. This means each nest represents a candidate solution, and each egg represents a feature. The initialization strategy is generating an initial population of n nests randomly by initializing each nest with a vector of binary value. Then according to a probability pa ϵ [0, 1]), it selects the worst nests and updating them using L'evy flight. Finally, BCS stops when the number of iterations reaches the maximum predefined by the user, and produces the best global nest. Algorithm 1 explains how BCS work.

In order to build binary vectors in local search, it employs equation (4) and equation (5) [19]:

t1

• ^{5 (} x ( i . j ) ) =----------------.                   ⁽⁴⁾

• 1    + e ^- x t ^{( j}

1, ^{5 (} x t ( i , j ) ) >  °

0, otherwise

(features) at nest i in iteration t.

• III.    The Proposed Algorithm

Feature selection based on hybrid binary cuckoo search and rough set theory in classification for nominal datasets (FS-BCS) uses BCS as a search technique to generate candidate feature subsets, and it uses objective function based on RSTDD to evaluate these candidates' features subsets to guide the BCS to reach best feature subset. This objective function is proposed by Jensen et al. [30] that selects the minimum number of selected features and maximum classification accuracy, it is shown in equation (6). The proposed FS-BCS is presented in Algorithm 1.

Objective Fuh.(R)=/r(D) *1C |  1R 1    (6)|C |

Where |C| is the number of conditional (total-class) features, |R| is the number of selected features, D is class, and Y r (D) is the dependency degree between feature subset (selected features) and class label.

Where о belongs to [0, 1], x^p stands for new eggs js

Input

• 1:    Number of nests N. // Each nest represent candidate feature subset

• 2:     Probability p a ϵ [0, 1].

• 3:    Maximum number of iteration T, initial iteration t=0.

Output

• 4:    Best global feature subset g_best.

Initialization (Initialize the population of nests and best global feature subset g_best).

• 5:      for i=1 to N do

• 6:               Generate Initial population of N candidate feature subsets x i randomly.

• 7:               Sort the x i descending according to value of objective function.

• 8:                Evaluate x i using equation (6).

• 9:                Best local feature subset=top candidate feature subset.

• 10:               g_best=best local feature subset.

• 11:      end for

Updating the population several time ( T times)

• 12:   Repeat

• 13:              Abandon a fraction p a of worse candidate feature subsets and updating them using L´evy flight.

• 14:              Evaluate each candidate feature subset in population

• 15:              Sort the population of nests descending according to value of objective function.

• 16:               Best local solution= top candidate feature subset in the population.

• 17:               If g_best< best local solution

• 18:                          g_best=local best solution.

• 19:                end if.

• 20:               t=t+1.

• 21:   Until t

• 22:   Produce the global best solution (g_best).

Algorithm 1. FS-BCS algorithm

• IV.    Evaluation

There are a number of potential ways to evaluate our approach. However, the most commonly used and perhaps provides comparative results on its efficiency is one that uses existing datasets, which have known features, and then compares our approach to a set of other competitive approaches. These are described below.

• A.    Datasets Selection

  To evaluate the performance of FS-BCS, a group of experiments have been run on five nominal datasets with different number of features (from 9 to 36), different number of objects (from 366 to 8124) and different number of classes (from 2 to 19). These nominal datasets are randomly selected from a set that has very little missing values from the University of California at Irvine, known as the UCI data repository of machine learning database [37]. Table 1 shows the selected datasets and their characteristics.

Table 1. Datasets

Dataset	Features	Objects	Classes
Breast-W	9	699	2
Mushroom	22	8124	2
Dermatology	34	366	6
Soybean(large)	35	683	19
Chess	36	3196	2

The following is a brief description of the datasets.

Breast-W. It is obtained from the university of Wisconsin hospitals, it has 9 features, and each one has ten distinct values. There are 699 objects, 458 objects classified into benign class, and the remaining objects are classified into malignant class.

Mushroom. It contains records drawn from the Audubon society field guide to North American mushrooms. This dataset has 22 features with different number of distinct values (from 2 to 12). Also, it has 8124 objects that are classified roughly into two classes.

Dermatology. This dataset has 34 features which have distinct values from 2 to 4. 366 objects are classified into six classes, 61 objects for first class, 112 objects for second class, 72 objects for third class, 52 for fourth class, 49 for fifth class, and 20 objects for sixth class.

Soybean (large). The task is to diagnose diseases in soybean plants. There are 304 objects which are classified into 19 classes.

Chess (King-Rook vs. King-Pawn). It has 36 features which have 2 distinct values. This dataset has 3196 objects, 1669objects belong to White can win class, and remaining objects belong to White cannot win class.

• B.    Evaluation Method

The indirect approach [2][57] is used to evaluate the developed algorithm, three comparisons are used in the experiments. First, “before and after comparison” is employed, which measures the classification accuracy of all available features and of the selected features. Secondly, our approach is evaluated against the Genetic algorithm [17] with Correlation based on Feature Selection (CFS) [38]. Thirdly, our approach is evaluated against PSO [39] with CFS [38]. Decision Tree (DT) [40] and Naive Bayes (NB) [41], which are two different classification algorithms (types), are used to measure the classification accuracy for all approaches that are used in the experiments. DT and NB are from the top ten data mining algorithms, and do not need complex initial parameters [42]. These are evaluated against three factors, their number of selected features, classification accuracy and number of iterations.

All implementations are run on a personal computer running Windows 8.1 with (i7), 3.0 GHZ processor and 16 GB memory. FS-BCS is implemented with PHP. The Genetic algorithm with CFS and PSO are known filter FS approaches, and are already implemented in the Weka tool [43]. The Genetic and PSO algorithms are selected, they are common NIAs for FS, and they are implemented in the Weka tool. CFS is an efficient objective function for FS, because it measures the redundant and relevant features in each candidate feature subset by evaluating the correlation between each feature and the class labels and between each pair of features using mutual information [38].

All parameters in these approaches are selected according to default parameters in the Weka tool, some of them are shown as follows: population size is 20, maximum number of iterations is 20, and the size of k is 10 objects in K-fold cross-validation which will be mentioned later in this section.

Each dataset was divided into two datasets randomly, training set, and a learning and test set. A training set that has about 70% of the dataset objects, and a learning and test set has about 30% of the dataset objects [44]. The training set is used by FS approaches to achieve features reduction. The learning and test set is used to build the classification model and estimates the performance of classification. We use K-fold cross-validation [45], also implemented in the Weka tool, to split the learning and test set into two disjoint sets to build the model and estimate the classification performance using DT and NB. When an object belongs to the test set, its class is hidden from the built classification model based on the learning set only.

In this work, we found, running the FS-BCS five times over a training set was sufficient to obtain good results, running the experiments longer than five times did not provide additional value. The best run, with the best classification accuracy, is selected.

• V.    Results and Discussion

In these experiments, classification Accuracy (Acc) is used to evaluate the classification performance, and Size Reduction percentage (SR %) is used to evaluate the percentage of removed features compared to all available features (or Subset Size (SS), which is the number of

Classification for Nominal Datasets selected features). In table 2, all means all features in a dataset. The best approach is the one that achieves maximum SR% without significantly reducing the classification accuracy compared to the total number of features in the least number of iterations [1]. Differences in accuracy is considered significant when it is more than 5% [46], and it is considered the same when it is less than 1% [47].

Table 2 shows that FS-BCS achieves better SR% without significantly reducing the classification accuracy in lesser number of iterations compared to the Genetic and PSO approaches. The main reason for these results is that BCS’s convergence is more efficient and faster compared to convergence of the PSO and Genetic approaches, because BCS uses efficient and simple hybrid mechanism [20] [19]. To be more specific, the local search in the BCS's hybrid mechanism plays the main role in the efficiency and speed of its convergence, because it uses levy flight technique to maximize the guarantee and speed of convergence [35]. The following subsections discuss the experiments results in more details in reference to SR%, "before and after FS" and a number of iterations.

• A.    Size Reduction Percentage and Classification Accuracy

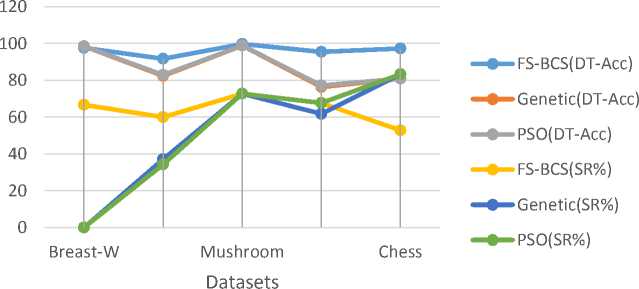
Table 2 and fig. 1 show the results of the comparisons between the FS-BCS, PSO and Genetic approaches.

The results show that FS-BCS achieves better FS for four datasets and the same for one dataset compared to the Genetic and PSO. In Breast-W dataset, FS-BCS achieves significant SR% (66.7%) compared to PSO and genetic (SR%=0), while the classification accuracy, according to DT and NB, is the same in the three approaches. FS-BCS achieves better SR% and classification accuracy according to DT and NB for Soybean (large). In Mushroom dataset, three approaches achieved the same FS (SR% and classification accuracy). But FS-BCS is capable to achieve better SR% and classification accuracy (DT and NB) in the dermatology dataset compared to the Genetic approach. Also in this dataset, FS-BCS achieves the same SR% and better classification accuracy (DT and NB) compared to PSO approach. The Genetic and PSO approaches achieve better SR% and significant reduction in classification accuracy (DT and NB) compared to FS-BCS, which achieves SR% without significant DT classification accuracy and improvement NB classification accuracy.

Table 2. Results of FS-BCS, genetic and PSO approaches

Dataset	Method	Size	SR%	DT Acc.	NBAcc.
Breast-W	All	9		93.9	96.1
	FS-BCS	3	66.7	97.6	98.1
	Genetic	9	0	98.5	98.1
	PSO	9	0	98.5	98.1
Mushroom	All	22		100	95.8
	FS-BCS	6	72.7	99.7	98.1
	Genetic	6	72.7	98.8	98.7
	PSO	6	72.7	98.8	98.8
Soybean (large)	All	35		92.3	92
	FS-BCS	14	60	91.7	90.7
	Genetic	22	37.1	82.4	85.3
	PSO	23	34.2	82.9	84.8
Dermatology	All	34		93.9	97.2
	FS-BCS	11	67.6	95.4	94.5
	Genetic	13	61. 6	76.3	86.3
	PSO	11	67.6	77.2	78.1
Chess	All	36		99.4	87.8
	FS-BCS	17	52.7	97.3	90.8
	Genetic	6	83.3	80.9	78.6
	PSO	6	80.9	81.2	83.3

All: Original Datasets. Size: Number of features. SR%: Percentage of size reduction against all features Acc: Accuracy.

CD сю

CD

CD

Datasets

—•—FS-BCS(NB-Acc)

—•—Genetic(NB-Acc)

—•—PSO(NB-Acc)

—•— FS-BCS(SR%)

—•—Genetic(SR%)

—•— PSO(SR%)

Fig.1. Comparisons between FS-BCS, genetic and PSO based on SR% and Classification Accuracy.

On average, in all datasets that are used in our experiment, FS-BCS achieves about 64% SR% and improves the DT and NB classification accuracy compared to the Genetic and PSO approaches, which achieve 50.9% and 51.6% SR% respectively

• B.    Classification Accuracy “before and after” FS-BCS, Genetic and PSO.

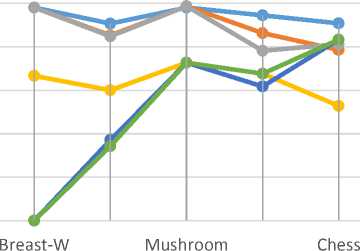
The results in Table 2 and fig. 2 show the classification accuracy according to DT and NB classification algorithms before and after running the FS-BCS, Genetic and PSO.

These results show that FS-BCS improves the classification accuracy-DT in breast-W and Dermatology datasets, as well as in the Soybean (large) and mushroom, while in the chess dataset, there is insignificant DT reduction. But the genetic and PSO achieve significant DT reduction in three datasets. According to NB classification algorithm, FS-BCS improves the NB in three datasets, and it achieves slight reduction, in NB, in two datasets, while the Genetic and PSO achieve significant reduction.

These results show that FS-BCS improves the classification accuracy-DT in breast-W and Dermatology datasets, as well as in the Soybean (large) and mushroom, while in the chess dataset, there is insignificant DT reduction. But the Genetic and PSO achieve significant DT reduction in three datasets. According to NB classification algorithm, FS-BCS improves the NB in three datasets, and it achieves slight reduction in NB in two datasets, while genetic and PSO achieve significant reduction.

Finally, according to DT and NB classification algorithms, FS-BCS succeeded to avoid significant reduction in classification accuracy for all the five datasets, while the Genetic and PSO failed to. Since FS-BCS is a general filter FS approach, it is efficient for DT and NB, which are different types of classification algorithms. According to [1], when a filter FS approach is efficient for DT and NB, it can be generalised for different types of classification algorithms, thus the results of FS-BCS.

Classification for Nominal Datasets

Q

го

о го

го

со

го

ого

го

IIII

Breast-W

Mushroom

Datasets

Chess

IIII

Breast-W

Mushroom

Chess

• ■    Before FS

• ■    After FS-BCS

• ■    After Genetic

• ■    After PSO

• ■    Before FS

• ■    After FS-BCS

• ■    After Genetic

• ■    After PSO

Datasets

Fig.2. Classification Accuracy Before and After FS

• C.    Analysis based on the number of iterations.

Table 3 and fig. 3 show the number of iterations needed to find the best solution for FS-BCS, genetic and PSO approaches. As shown, FS-BCS requires the least number of iterations compared to genetic and PSO in all datasets to reach the best solution. FS-BCS was able to find the best solution in 25% and 34% (these percentages are the average of all datasets) from the number of iterations in the Genetic and PSO respectively.

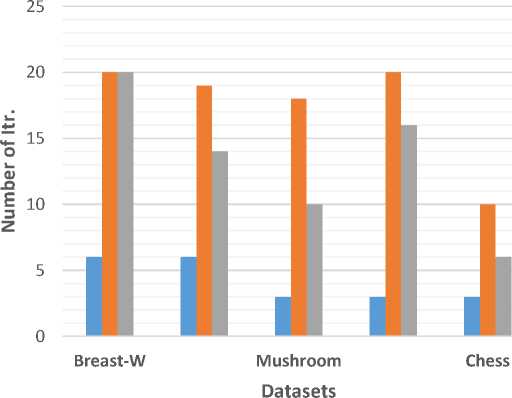
Fig.3. C omparisons between FS-BCS, genetic and PSO based on number of iterations

■    FS-BCS ■    Genetic ■    PSO

Table 3. Number of iterations of FS-BCS, genetic and PSO approaches

Dataset	FS-BCS	Genetic	PSO
Breast-W	6	20	20
Mushroom	6	19	14
Soybean (large)	3	18	10
Dermatology	3	20	16
Chess	3	10	6

• VI.    Conclusion

BCS has quick and efficient convergence, less complexity, easier to implement, and fewer parameters compared to other NIAs such as ACO, ABC and PSO, and thus is increasingly used in many algorithms as a search technique. Similarly, RSTDD is used in many filter FS approaches as an objective function, for its relatively cheaper, easier to implement characteristics, and does not need any preliminary or additional information.

This paper proposed a new algorithm, FS-BCS, as a classification filter FS approach for nominal datasets using BCS and RSTDD to achieve significant SR% without significantly reducing the classification accuracy compared to the total number of features in lesser number of iterations. According to our knowledge, FS-BCS is the first approach that combines the BCS with RSTDD.

The experimental results show that FS-BCS achieved better FS in four datasets, and same FS in the fifth dataset compared to known filter FS approaches (PSO and Genetic) in the Weka tool implementations.

On average, FS-BCS achieved significantly higher SR% and improved the DT and NB classification accuracy compared to the Genetic and PSO approaches. Also our approach succeeded to maximize the SR% without significantly reducing the classification accuracy compared to the total number of features for all datasets, while PSO failed to do so in two datasets and Genetic failed in three datasets. Our approach also took lesser number of iterations to reach the best solution compared to PSO and genetic approaches. On average our approach needed significantly lesser number of iterations than those needed in Genetic and PSO.

Although these results show that BCS with RSTDD has faster and more efficient convergence compared to PSO and Genetic approaches, the authors appreciate further experiments would needed to evaluate the scalability of the proposed approach on large high dimensional datasets.