Феноменологическая модель динамики городской агломерации: теоретический аспект

DOI:

Цитирование. Киселева Н. Н., Киселев В. В., Бавина К. В., Кальянова Е. Г., 2019. Феноменологическая модель динамики городской агломерации: теоретический аспект // Региональная экономика. Юг России. Т. 7, № 2. С. 46–59. DOI:

Постановка проблемы

В настоящее время ряд ученых и практиков в сфере урбанистики связывает перспективы пространственного развития с усилением агломерационных тенденций. В своем выступлении на Гайдаровском форуме в январе 2019 г. мэр Москвы С.С. Собянин отметил, что для обеспечения роста экономики нужно отдать приоритет финансированию крупных городов и агломерации. Однако каждая агломерация имеет свою емкость и, достигнув определенного порога, агломерационный эффект рассеивается. Устойчиво наблюдаемый феномен поляризации экономического пространства устанавливает определенный баланс издержек и выгод, таким образом, эффекты дезэкономии уравновешиваются положительными эффектами экономии различного вида. Возникает вопрос, может ли сохраняться такой баланс при отсутствии ограничений роста объемов производства и, соответственно, размеров города?

Внутренние закономерности развития агломерации и ее роль в пространственной организации региона могут быть описаны с помощью математических моделей, позволяющих выявить объективные закономерности динамики концентрации населения и экономической активности. Полученные оценки могут быть использованы при принятии решений о финансовой и иных формах поддержки муниципальных образований, а также при определении стратегических приоритетов их развития.

Обзор литературы и методы

В настоящее время хрестоматийными признаны три научных направления, в рамках которых строились модельные представления и достигалось теоретическое понимание природы агломерационного процесса:

• 1)    неоклассическая теория [Samuelson, 1964; Balassa, 1985];

• 2)    новая теория торговли [Krugman, 1980; Brülhart, Torstensson, 1996];

• 3)    новая экономическая география [Krugman, 1994; Venables, 1996; Krugman, Venables, 1996; Fujita, Thisse, 2002; Head, Mayer, 2004; Fujita, 2007].

Последнее направление объясняет природу агломерационных процессов действием центростремительных и центробежных сил. Генерирование центростремительных сил происходит в недрах общественного сознания людей, которые достигли понимания того, что повышение качества жизни и более комфортная среда для развития бизнеса и получения доходов увеличиваются при скоплении промышленного производства и концентрации взаимосвязанного населения в городе (городах) и прилегающих поселениях, приводит к существенному повышению экономической эффективности (нечто подобное проявляется в биологических популяциях и носит название «эффект группы») и возникновению условий для развития инновационной среды. В результате формируется оптимальная транспортно-логистическая сеть, реализуются скоординированные системы территориального планирования и использования земель, проводится согласованная экологическая политика, реализуются крупные инфраструктурные проекты, в том числе за счет федеральных средств, комплексное строительство коммунальной инфраструктуры, сбалансированное развитие торгово-развлекательной и социальной инфраструктур, создаются условия для гетерогенности в отраслевой и профессиональной структурах занятости населения и т. п. Негативные последствия высокой концентрации населения (экологическая, социальная, экономическая напряженность и др.) относят к центробежным силам, которые влекут снижение концентрации экономической активности.

Современное представление о городских агломерациях полагает в основу их возникновения существование крупных городов – центров в промышленных районах с высокой плотностью населения, где концентрация экономической активности в пределах обозначенной территории сопровождается формированием общей социально-экономической системы.

Значительное число работ посвящено изучению закономерностей развития отдельных подсистем городской агломерации [Groot, Poot, Smit, 2007; Greenstone, Hornbeck, Moretti, 2007; Chang, Oxley, 2009; Новосельцева, 2011; Растворцева, 2013; Панина, 2013; Carlino, Kerr, 2014].

Ответ на вопрос о характере динамики агломерационного процесса может быть получен при анализе синергической составляющей центробеж- ных и центростремительных агломерационных сил, которые возникают в результате экономических отношений между агентами на урбанизированной территории. Выявление закономерностей эволюции городской агломерации, как и любой большой системы, может стать предпосылкой для построения некоторой модели динамики концентрации экономической активности населения, основанной на использовании математических методов. В настоящее время можно отметить существование двух стратегий использования математического аппарата для описания больших адаптивных динамических систем.

Методологическую основу первой стратегии составляют системный анализ и представление о городской агломерации как о сложной единой социально-экономической инвестиционной системе в составе некоторого природно-территориального комплекса с общей инженерной инфраструктурой и единой коммуникационной системой. В математическом смысле исследование городской агломерации в рамках рассматриваемой стратегии приводит к построению имитационных или (и) эконометрических моделей и их всестороннему анализу. На таких моделях можно исследовать влияние разных совокупностей агломерационных сил, их корреляционных связей на агломерационный эффект, возможен поиск оптимальной структуры городской агломерации для достижения соответствующих характеристик пространственно-временной динамики агломерационного процесса.

Возможен сценарный анализ формирования агломерации с заданными параметрами и свойствами и др. Например, модельный анализ агломерационного процесса в работах [Puga, Venables, 1969] дал объяснение эффекту «разлета» отраслей промышленности от одного региона к другому (феномен «летящие гуси») [Растворцева, 2013]. Изучение городской агломерации в рамках первой стратегии дает возможность учесть воздействие большого числа разнообразных агломерационных сил и включить их в различные сценарии взаимодействия, но при этом не позволяет получить аналитические результаты, характеризующие фундаментальные свойства агломерационного процесса.

Вторая стратегия исследования агломерационного процесса с использованием математического инструментария базируется на феноменологическом описании городской агломерации как системы с применением метода фазовых портретов [Киселева, Киселев, Бавина, 2018]. Феноменологическое описание выполняется с помощью фазового пространства (xi), динамичес- кого пространства (xi, t), пространства параметров (ak) и некоторой математической модели, где xi – переменные; ak – параметры, которые являются константами данного агломерационного процесса, однако в общем случае – зависящими от некоторых других величин; t – время. Важнейшим и наиболее ответственным этапом при такой стратегии обращения к математическим методам является обоснование выбора основных фазовых переменных, так как эти переменные в конечном итоге через модель представляют и характеризуют закономерности агломерационного процесса, они лежат в основе выводов.

Таким образом, городская агломерация и ее пространственно-временная динамика описываются некоторым множеством параметров и фазовых переменных с разными характерными временами, то есть с существенно различными масштабами времени. Такие системы при их исследовании обычно неформальным путем разбиваются на подсистемы, содержащие не более трех масштабов времени, с которыми связывают быстрые, основные и резервуарные переменные (в терминах теоремы Корзухина) [Жаботинский, 1974]. Из теоремы Корзухина следует, что подпадающие под условия этой теоремы большие системы характеризуются сложным поведением, в том числе автоколебательным режимом. Их состояние с временным запаздыванием или без запаздывания синхронизируется с внешними силами, которые для городской агломерации могут быть как центростремительными, так и центробежными. Основные составляющие агломерационного процесса генерируются поведением народа, которое направлено на рост личного благосостояния и повышение уровня качества жизни. В отдельных случаях агломерационными силами выступают нормативные правовые документы, которые также являются механизмами регуляции агломерационного процесса и численности населения. Этого достаточно, чтобы для анализа предпосылок концентрации экономической активности населения его численность была выбрана в качестве главной фазовой переменной.

Быстрые переменные городской агломерации ассоциированы с информационными и цифровыми технологиями, банковскими, юридическими, медицинскими, образовательными, туристскими, культурологическими, спортивными и прочими услугами, инвестициями. Резервуарные переменные связанны с природно-климатическими характеристиками, возведением объектов инфраструктуры, ад- министративно-территориальным делением, специализацией региона. Быстрые переменные не оказывают никакого влияния на запаздывание системы, которая лишена этого эффекта по отношению к их воздействию, время релаксации регулирующего механизма равно нулю. Эти переменные являются безынерционными, мгновенно «настраиваются» на состояние системы (на значение основной фазовой переменной) и принимают стабильные значения. Результатом воздействия быстрых переменных на агломерационный процесс можно пренебречь и при математическом моделировании их можно не включать в модель. Резервуарные переменные на временах «горизонта прогнозирования» эволюции агломерации считаются постоянными и не лимитируют развитие агломерации. Их влияние на агломерационный процесс носит дискретный характер. Математически это можно учесть с помощью параметров, которые скачкообразно изменяются в отдельные моменты времени, а также с помощью изменения начальных условий и введения новых параметров в модель.

Если в качестве основной фазовой переменной городской агломерации выбрана численность (концентрация) населения как показатель концентрации экономической активности, то наиболее простым фазовым пространством, в котором строятся и изучаются фазовые портреты, является плоскость x 0 y , где x – численность (концентрация) населения, y – показатель изменения численности (концентрации) населения.

Имеются яркие работы, демонстрирующие плодотворность применения феноменологического анализа в научных исследованиях в самых различных областях знаний – биологии, экологии, химии, экономике и др. [Колмогоров, 1972; Молчанов, 1975; Исаев и др., 2001].

Математический аппарат качественных исследований динамических систем подробно описан в соответствующей литературе, и результаты этих исследований являются хрестоматийными [Якобсон, 1976; Арнольд, 1978].

Регулирующие механизмы динамики городской агломерации и ее фазовые портреты

Дадим феноменологическое описание динамики городской агломерации. Первой фазовой переменной x мы определяем численность населения, а второй – y – изменение численности,

x(t + At)                                      ~ y =   , ' за некоторый дискретный времен- x (t)

ной интервал Δ t , длительность которого определяется горизонтом прогнозирования и наличием исходного эмпирического материала службы статистики (год или два). В этом случае функция y = y ( x ) может быть найдена экспериментально, а ее график принято называть фазовой траекторией. Значение x = x ₀, при котором выполняется равенство y ( x ) = 1, принято называть равновесным, или стационарным, а точку x = x ₀ – стационарной точкой, или особой (критической) точкой. При y ( x ) = 1 для любого значения x особые точки полностью заполняют прямую y = 1 . На этой прямой агломерационные центробежные и центростремительные силы уравновешиваются, численность населения не изменяется.

При y ( x ) > 1 численность населения увеличивается и с большой уверенностью можно утверждать, что в городской агломерации преобладают центростремительные силы, происходит рост концентрации экономической активности. При обратном неравенстве y ( x ) < 1 численность населения снижается, центробежные силы преобладают над центростремительными, наблюдается снижение концентрации экономической активности.

Если y ( x ) = 1, то соотношение центробежных и центростремительных сил и вид функции y = y ( x ) определяют характер равновесия на урбанизированной территории. Оно может быть устойчивым или неустойчивым. Если равновесие является неустойчивым, то происходит или концентрация экономической активности до максимально возможных значений в пределах некоторой территории, или ее катастрофическое снижение. Характер устойчивого равновесия может быть различным и зависит от типа особых (критических) точек, являющихся решением уравнения y ( x ) = 1 . В частности, могут наблюдаться автоколебания, затухающие колебания, колебания с возрастающей, но ограниченной в асимптотике амплитудой, монотонное достижение стабильного равновесия сверху или снизу (логистическая зависимость), предельные устойчивые, полуустойчивые или неустойчивые циклы различной длины.

Характерная особенность автоколебаний – отсутствие внешнего периодического воздействия. Возникают вопросы о том, какова амплитуда, период, другие характеристики колебательного процесса, какова его эволюция, может ли колебательный режим постепенно измениться и через какое время колебания исчезнут. Это вопросы управления адаптивной системой, которые могут быть исследованы в данном случае только качественно, например, методом анализа фазовых портретов.

С математической точки зрения подобные задачи относятся к теории катастроф, крайне сложные для решения [Чиллингоурт, 1979]. Тем не менее эта теория нашла широкое применение в исследовании устойчивости структур самой различной природы и самых разнообразных типов.

При анализе фазовых портретов будем учитывать такую особенность городской агломерации, как ее крупность (Развитие городских агломераций, 2015). На практике различают малые агломерации – до 0,5 млн чел., большие – от 0,5 до 0,75 млн чел., крупные – от 0,75 до 1 млн чел. и крупнейшие – свыше 1 млн чел. На фазовой плоскости x 0 y эти граничные или пороговые значения численности обозначим x _min и x _max, советующие минимальной и максимальной численности. Необходимо учитывать их при анализе центробежных и центростремительных сил, так как с этими параметрами связываются важнейшие составляющие агломерационного процесса, определяющие его градиент. Это интенсивность и направление миграционных потоков населения, которые определяют пространственно-временную динамику агломерации. При достижении численности населения своего максимального значения x _max и сохранении его роста напряжение критической перенаселенности может быть снято реализацией одного из двух вариантов развития событий. Первый из них и неизбежный при условии сохранения агломерацией исходного статуса крупности предполагает миграцию населения на другие территории. В этом случае агломерация становится агломерацией-донором населения до тех пор, пока выполняется неравенство y ( x ) > 1 .

Второй вариант разрешения проблемы избыточности населения предполагает изменение ранга крупности агломерации и переход ее в более высокий. Это влечет скачкообразное изменение значения параметров x _min и x _max, соответствующую трансформацию и перестройку взаимосвязей, механизмов ее функционирования, территориальное изменение границ и т. п. со всеми вытекающими отсюда последствиями, которые неизбежно будут сказываться на агломерационном эффекте.

При доминировании центробежных сил (в этом случае y(x) < 1) численность населения агломерации снижается до предельно минимального уровня xmin, отмечается утрата агломерационных эффектов и других преимуществ высокой концентрации населения. Теоретически можно предвидеть развитие ситуации по трем сценариям. Если в ранжированном ряду агломераций по их крупности рассматриваемая агломерация является малой, то она, как феномен, либо прекращает свое существование (сценарий 1), либо продолжает функционировать за счет иммигрантов из донорных по населению территорий и становится агломерацией-акцептором (сценарий 2), либо переходит в более низкий ранг крупности, если ее место в ряду не является самым низким (сценарий 3).

Конечно, отождествление реальных процессов – центробежных и центростремительных сил агломерационного процесса – с переменными и параметрами феноменологической модели, объясняющей пространственно-временную динамику основной фазовой переменной, равновесие системы, появление предельных циклов, стационарных и затухающих автоколебаний, даже путем простого моделирования является все-таки сложной задачей.

Общее качественное поведение системы во всем динамическом пространстве проявляется при t→∞, когда ее асимптотические характеристики не зависят от начальных условий. Наиболее важными решениями являются стационарные точки и предельные циклы. Вопрос об устойчивости и характере стационарных точек напрямую связан с качественной картиной фазового портрета в их окрестности и его топологией. Выше мы говорили, что вид фазовых портретов зависит от параметров и функциональной зависимости одной фазовой переменной от другой, определяющей тип особой точки: устойчивый узел, седло, устойчивый фокус, центр или еще какая-либо сложная особая точка.

Нахождение автоколебаний – одна из основных задач при исследовании поведения систем. Однако общих аналитических методов для ее решения и выявления механизмов, ответственных за возникновение автоколебаний, не существует. Можно лишь утверждать, что если при t →∞ основная фазовая переменная x →∞ , то модель является неполной и обладает небольшой предсказательной силой. Если из любой точки первого квадранта изображающая точка состояния агломерации за некоторое время достигает одного из положений равновесия (устойчивого или неустойчивого), либо переходит в режим автоколебаний, то можно полагать, что модель правильно отражает качественное поведение оригинала.

Теоретическую кривую y = y ( x ) на фазовой плоскости x 0 y для фиксированных значений всех параметров обозначим y ₀ = y ( x ). Такая кривая называется статической. Рассмотрим изменение ее положения на примере отдельного фрагмента кривой y ₀ = y ( x ) в виде монотонно убывающей функции для различного соотношения агломерационных сил (рис. 1).

Превышение суммы центростремительных сил над суммой центробежных «приподнимает» кривую y ₀ над осью 0 x (см. рис. 1, кривая II), в слу-

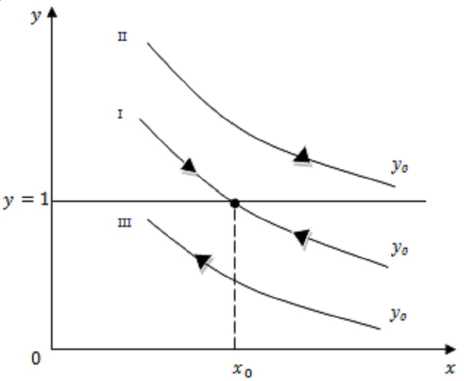
Рис.1. Изменение положения статической кривой y ₀ на фазовой плоскости x 0 y при различном соотношении центростремительных ( F _цс.) и центробежных ( F _цб.) сил:

I – положение кривой с одной устойчивой точкой равновесия x ₀, центробежные и центростремительные силы равны ( F _цс. = F _цб.), численность населения не меняется или колеблется в окрестности x ₀, y ₀( x ₀) = 1;

II – то же, F _цс. >  F _цб., численность населения увеличивается, y ₀( x ₀) > 1 для всех x из области определения;

III – то же, F _цс.<  F _цб., численность населения уменьшается, y ₀( x ₀) <  1 для всех x из области определения Примечание. Составлено авторами.

чае их равенства кривая y ₀ пересекает y = 1 в некоторой точке x ₀, она является устойчивой, и в агломерации достигается стабильное состояние (см. рис. 1, кривая I), характер которого определяется типом особой точки x ₀. Если центробежные силы больше центростремительных, то кривая y ₀ целиком находится ниже прямой y = 1, оставаясь в первом квадранте (см. рис. 1, кривая III).

Еще раз подчеркнем, что на рисунке 1 приведен лишь пример фрагмента некоторой истинной кривой y ₀, которая фактически может иметь куда более сложный вид, нежели монотонно убывающая функция.

Наиболее популярные эвристические и теоретические фазовые портреты больших систем для отдельных фрагментов статической кривой y ₀ в плоскости x 0 y представлены на рисунке 2 с одной ( а , б ) или двумя ( в, г ) точками равновесия.

На каждом рисунке представлены фазовые траектории для различных типов особой точки x _уст. и x _неуст., поэтому они изображены пересекающимися.

Характер или тип особой (критической) точки, которая является решением уравнения у0(х) = 1, определяется видом статической кривой у0. Ранее мы, ссылаясь на общеизвестные математические постулаты, говорили, что численность населения городской агломерации при определенных условиях на функцию y = у0(х), которая описывает изменение состояния агломерации в стабильных условиях, может с течением времени: снижаться до состояния утраты всех агломерационных эффектов; стабилизироваться на некотором уровне; испытывать периодические колебания.

В соответствии с типом особой точки динамические фазовые портреты системы в плоскости t 0 x также могут быть самыми разнообразными: режим автоколебаний с циклами различной длины, затухающие колебания, стабильное состояние покоя, логистическая зависимость, x ( t ) → 0 или x ( t ) →∞ в асимптотике при t →∞ , другие режимы. В ряде случаев фазовые траектории, окружающие особую точку типа центр, являются замкнутыми и тогда в системе появляются предельные циклы. Устойчивые предельные циклы являются математическими образами автоколебаний.

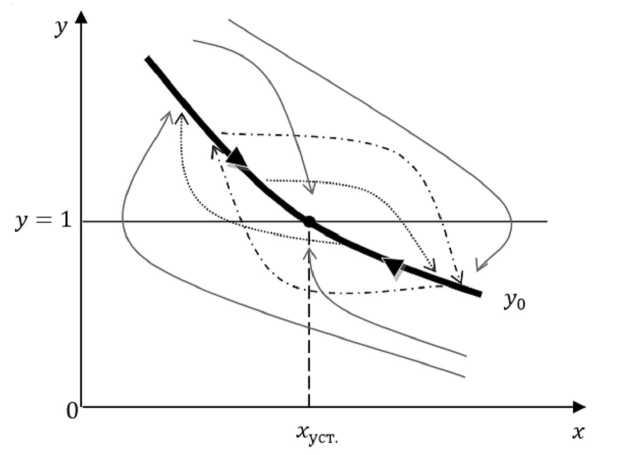
а )

Рис. 2. Фрагменты фазовых портретов городской агломерации в плоскости x0y для различных видов статической кривой y ₀ (см. также с. 53 и 54):

x – численность населения городской агломерации; y – изменение численности городской агломерации; y ₀ – статическая кривая зависимости y = y(x) для стабильных условий;

---------->     возможные фазовые траектории для различных типов особой ----------------->       точки x уст. или x неуст.

• а ) y ₀ – убывающая функция с одной устойчивой точкой равновесия x _уст., механизм регуляции численности населения агломерации основан на принципе отрицательной обратной связи

  у¹¹

  
  
  

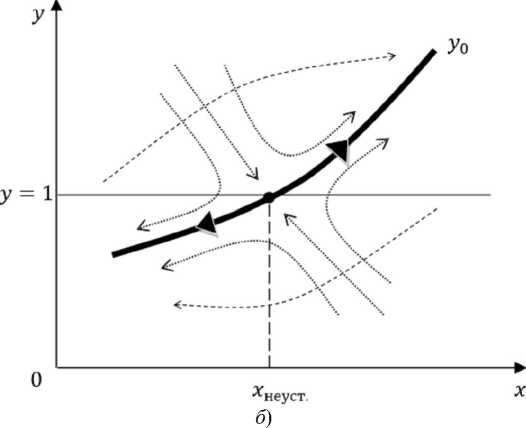
  Рис. 2. Продолжение:

  б ) y ₀ – возрастающая функция с одной неустойчивой точкой равновесия x _неуст., механизм регуляции численности населения агломерации основан на принципе положительной обратной связи

  
  
  

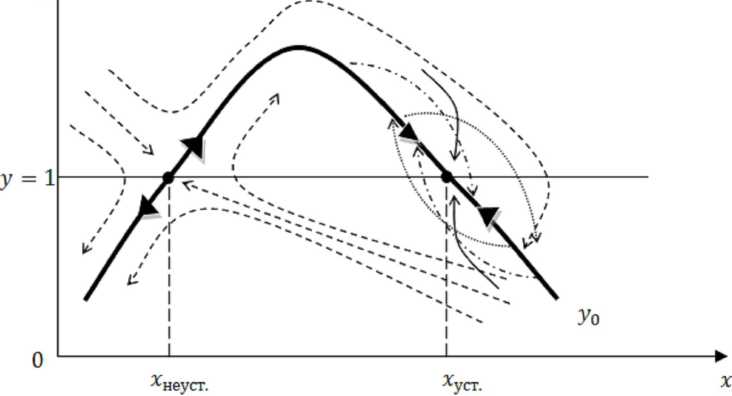
  в )

  
  

Рис. 2. Продолжение:

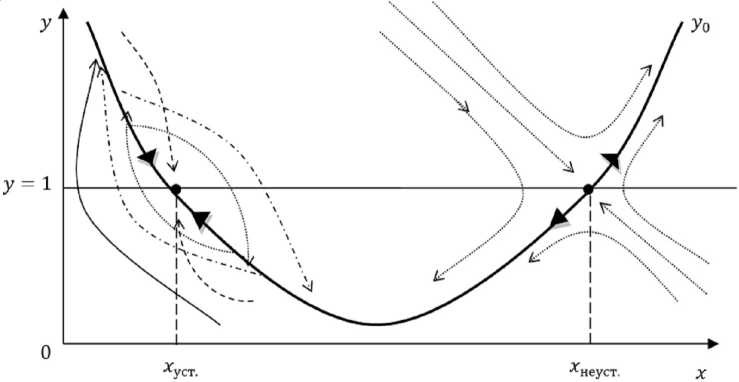
• в ) y ₀ – выпуклая вверх функция с двумя точками равновесия – устойчивой x _уст. и неустойчивой x _неуст., механизм регуляции численности населения в окрестностях точек x _уст. и x _неуст. таков, как указано в подписи к рис. 2, а и 2, б

  

  г )

  Рис. 2. Продолжение:

  г ) y ₀ – выпуклая вниз функция с двумя точками равновесия – устойчивой x _уст. и неустойчивой x _неуст., механизм регуляции численности населения в окрестности точек x _уст. и x _неуст. таков, как указано в подписи к рис. 2, а и 2, б

  
  
  

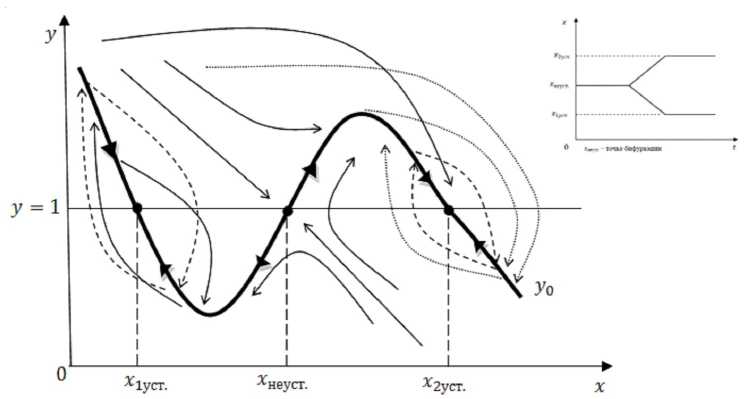
  Рис. 2. Окончание:

  
  

д ) y ₀ – немонотонная функция с тремя точками равновесия – x _1уст., x _2уст. и x _неуст., механизм регуляции численности населения в окрестности точки x _неуст. может быть как отрицательным ( x <  x _неуст.), так и положительным ( x >  x _неуст.)

Примечание. Составлено авторами.

Кроме вышеописанных режимов, важна оценка устойчивости агломерационного процесса и нахождение предпосылок для возникновения бифуркаций. Они возникают тогда, когда в динамике взаимодействия центробежных и центростремительных сил рождается точка, переход через которую приводит траекторию развития динамической системы к разветвлению. В этом случае исследуемые качественные свойства объекта не являются одинаковыми для всех значений некоторых параметров модели. Определение потенциала центробежных и центростремительных сил, который приводит к разрывному изменению сложившегося в регионе агломерационного процесса, фактически означает нахождение бифуркационных значений параметров, при которых происходит качественное изменение фазового портрета. В этом случае напряжение центробежных и центростремительных сил разрешается прохождением через точку бифуркации. На рисунке 2, д точка x = xнеуст. является точкой бифуркации, на фрагменте показан динамический фазовый портрет, возможен перескок изображающей точки с одной ветви на другую.

Городская агломерация, как система, может обладать еще одной особенностью: проявлением режима динамического хаоса. Хаотическое поведение динамических систем возникает в детерминированных дифференциальных или разностных нелинейных системах, в которых имеет место существенная зависимость от начальных условий. Любое малейшее изменение начальных условий приводит к кардинальному изменению поведения системы. Характерной особенностью хаотических систем является наличие странных аттракторов – областей притяжения с фрактальной структурой [Тарасевич, 2003]. В рамках рассматриваемой феноменологической модели вида xn+1 = f(xn), на которую мы фактически опираемся, система может перейти к хаосу. Некоторые исследователи агломерационных процессов считают актуальным использование теории фракталов при упорядочивании иерархии поселенческих систем, которые кажутся хаотичными [Павлов, 2013]. К сожалению, качественный анализ динамического хаоса практически невозможен.

Зарождение и эволюция городской агломерации с граничными значениями по численности населения могут быть объяснены в рамках фазового портрета на рисунке 3.

Приведем пример фазового портрета городской агломерации, который демонстрирует плодотворность предложенного метода исследования динамики концентрации населения вокруг города-центра. Обратимся к фактическим данным о народонаселении Владивостокской городской агломерации по годам и рассчитаем показатель темпов его изменения (см. таблицу). Агломерация является крупной, моноцен-трической, доля населения города-ядра на 2018 г. составляла 77,9 % от общей численности агломерации.

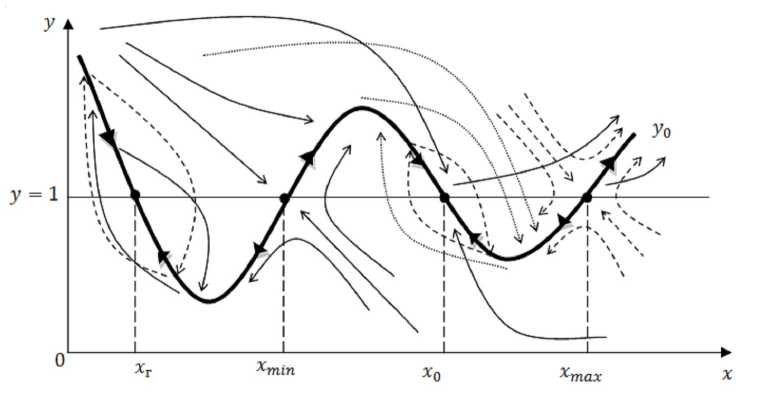
Рис. 3. Фазовый портрет городской агломерации:

х _г – равновесное состояние города-ядра; х _min – точка зарождения городской агломерации, начало проявления агломерационных эффектов; х ₀ – стабильное состояние городской агломерации; х _max – точка перехода городской агломерации в более высокий ранг крупности;

у ₀ – статическая кривая концентрации экономической активности; х _min и х _max – точки бифуркации Примечание. Составлено авторами.

Таблица

Динамика численности жителей поселений Владивостокской городской агломерации

Численность населения	2002 г.	2004 г.	2006 г.	2008 г.	2010 г.	2012 г.	2014 г.	2016 г.	2018 г.
г.о. Владивосток	594,7	616,8	610,2	605,4	604,8	622,7	630	633,2	633,1
г.о. Артём	110,9	111,4	111,6	111,9	111,2	112,3	111,8	114,9	116,2
Надеждинский район	40,2	40,2	38,8	38,7	39,1	38,9	38,2	38,5	38,7
Шкотовский район	25,8	25,6	25,6	25,6	24,5	24,3	24,2	24,5	24,2
Итого численность городской агломерации, x n	771,6	794	786,2	781,6	779,6	798,2	804,2	811,1	812,2
Изменение численности, x„ + 1 У п = ~— x	–	1,029031	0,990176	0,994149	0,997441	1,023858	1,007517	1,00858	1,001356

Примечание. Рассчитано авторами.

Соответствующий статистическим данным таблицы фазовый портрет Владивостокской городской агломерации представлен на рисунке 4.

Фазовая траектория – это линия, последовательно соединяющая изображающие точки на фазовой плоскости по годам, координатами которых являются численность населения x и показатель изменения численности y за промежуток времени в два года. Направления стрелок указывают ход времени. На рисунке представлен гипотетический вид статической кривой y ₀. На фазовой кривой можно выделить две характерные стадии изменения численности населения. Это гетероциклическая стадия с 2002 по 2010 г., длительность которой составила 8 лет, и стадия увеличения численности с 2010 г. по настоящее время, длительность которой не менее 8 лет. Прирост народонаселения за рассматриваемый период составил 5,3 %, но его темп снижается, за последние два года не превышал 0,14 %, статическая кривая y ₀ является убывающая функция. При сохранении существующего баланса сил ожидается стабилизация численности населения на уровне 815–820 тыс. человек.

Заключение

Типы динамики городской агломерации, стадии ее развития и наличие количества и типа особых точек характеризуют предельные проявления особенностей этого многогранного явления. В научных исследованиях математическая модель служит средством получения дополнительной информации об объекте изучения, позволяет оценить границы его прогнозируемого поведения, проверить возможности управления состоянием системы, обеспечивая новыми сведениями построение теории и отдельных практических приложений. Качественное исследование фазовых портретов городских агломераций будет способствовать решению задач поиска идентификационного образа агломерации, разработке методов прогнозирования пространственно-временной динамики концентрации экономической активности населения и нахождению количественных оценок агломерационного эффекта.