Ферримагнитные пирротины в метастабильном состоянии

У природных минералов состава Fe 0 , 908 S– Fe 0,873 S (пирротинов) зависимость намагниченности от температуры имеет ряд специфических особенностей [1–5]. Например, γ-превращение проявляется в виде резкого изменения намагниченности при температурах 220…280 °С [1; 3]. У искусственных сульфидов железа наблюдалось низкотемпературное ( Т = 45 К) изменение намагниченности [4]. Часто у ферримагнитных сульфидов железа отмечается так называемый температурный магнитный гистерезис, т. е. несовпадение намагниченности до и после термообработки. Максимальный температурный гистерезис наблюдается у образцов практически с нулевой намагниченностью в исходном состоянии [6]. Такое изменение намагниченности определяется не только перераспределением вакансий в кристаллической структуре, но и другими, до настоящего времени пока еще мало изученными явлениями [6–8].

Пирротины обладают кристаллическим строением типа NiAs, в котором часть катионных позиций вакантна. Поскольку между базисными плоскостями реализуется антиферромагнитное спиновое упорядочение, а в базисных плоскостях – ферромагнитное, то тип распределения вакансий (сверхструктура) определяет величину неcкомпенсированного магнитного момента подрешеток [9–13]. Распределение вакансий на подрешетках находится в непосредственной зависимости от температуры, давления и химического состава сульфидов железа [10–14]. Процессы перераспределения вакансий в структуре осуществляются в результате диффузии, поэтому при воздействии на пирротины высокой температуры с последующей закалкой можно получать различные неравновесные распределения вакансий в структуре, т. е. пирротины в метастабильном фазовом состоянии.

Необходимо изучить температурные изменения намагниченности пирротинов в метастабиль-ном фазовом состоянии, обладающих максимальным температурным магнитным гистерезисом, а также объяснить эти изменения в рамках существующих теоретических моделей.

Образцы для исследований, в исходном состоянии обладающие практически нулевой намагниченностью, были получены как методом сухого синтеза (серия А), так и в результате разложения в вакууме пирита (FeS2) при различных температурах (серия Б) [6; 11; 16]. После синтеза образцы прокаливались при различных температурах, закаливались и исследовались на термобаллистической установке в поле 1 кЭ. Химический состав и кристаллическая структура полученных образцов анализировались на рентгеновском дифрактометре ДРОН-3 по описанным в литературе методикам [3; 10]. Мессбауэровские спектры снимались с источником Со57 в матрице Cr.

Явление уменьшения намагниченности пирро-тинов, синтезированных и затем закаленных от 1 000 °С, установлено давно и является прямым следствием фазовых диаграмм [2; 3; 9–11; 14]. Сам факт уменьшения намагниченности пирро-тинов при закалке от высоких температур является обычным результатом, однако намагниченность в большинстве случаев до нуля не спадает. Представляет особый интерес тот случай, когда при закаливании получались образцы с нулевой намагниченностью. При нагревании таких образцов со скоростью 5 град/мин в поле 1 000 Э до температуры 350 °С наблюдался переход их в ферримагнитное состояние.

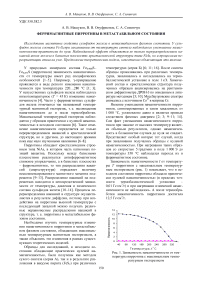
Зависимость намагниченности I от температуры Т пирротинов с максимальным температурным гистерезисом (рис. 1) показывает, что в исходном состоянии пирротины обладали практически нулевой намагниченностью (в пределах точности термобаллистической установки – 0,01 Гс∙см³/г) и при нагревании изменений намагниченности не наблюдалось. А после термообработки намагниченность пирротинов достигала 12,5 Гс∙см³/г.

0 I" ■,■ ■,■ ■,■ ■■■ ■■■ ■■■     *,

Температура, t С

Рис. 1. Зависимость намагниченности от температуры пирротина с максимальным температурным гистерезисом

Определение химического состава исследуемых пирротинов по принятой рентгеновской методике (по угловому положению рентгеновских рефлексов) вызывает трудности. Например, наиболее чувствительный к химическому составу рентгеновский рефлекс (102) после температурного воздействия смещался, т. е. угловое положение данного рентгеновского рефлекса после термообработки пирротинов изменялось (рис. 2). Однако по совокупности экспериментальных фактов химический состав таких пирротинов соответствовал формуле Fe7S8. Рентгеновские ис- следования показали, что в исходном состоянии образец обладал гексагональной структурой, а в конечном – моноклинной, но моноклинной структурой состав Fe7S8 может обладать в очень узкой области гомогенности [2; 3; 9–11; 14].

Рис. 2. Профиль рентгеновского рефлекса (102) пирротина с максимальным температурным гистерезисом до нагрева ( а ) и после ( б )

Сравнение профиля рентгеновского рефлекса (102) образца в исходном (рис. 2, а ) и в конечном состоянии (рис. 2, б ) показывает, что одиночный рентгеновский рефлекс в конечном состоянии расщепляется на пять близко расположенных рефлексов, соответствующих моноклинным искажениям структуры.

Мессбауэровские спектры пирротина (рис. 3) демонстрирует, что в начальном состоянии спектр ядерного гамма-резонанса (ЯГР) состоит из одного секступлета с ассиметричным уширением линий (рис. 3, а), а конечное состояние характеризуется с тремя хорошо разрешенными секступлетами(рис. 3, б). Анализ этих спектров говорит о том, что в конечном состоянии катион- ные вакансии упорядочены в четных (нечетных) базисных плоскостях. Это соответствует структурному переходу В8–С6 в промежуточной стадии. Катионы в такой структуре имеют соответственно 0, 2 и 4 вакансии во второй координационной сфере. Такие позиции соответствуют локальным магнитным полям 305, 275 и 225 кЭ на ядрах. Расчет заселенности позиций в этой структуре следующий N0 = 0,47; N1 = 0; N2 = 0,39; N3 = 0; N4 = 0,23. Заметим, что вакансии при случайном законе распределения должны иметь заселенности N0 = 0,21; N1 = 0,3; N2 = 0,31; N3 = 0,14; N4 = 0,05, где N0, N1, N2, N3, N4 – заселенности позиций без вакансий, с одной вакансией, двумя, тремя и четырьмя вакансиями соответственно.

Рис. 3. Спектры ядерного гамма-резонанса пирротина с максимальным температурным гистерезисом до нагрева ( а ) и после ( б )

Обработка спектра пирротина в начальном состоянии позволяет предположить наличие в нем дополнительных секступлетов. Удовлетворительной оказалась аппроксимация спектра пятью сек-ступлетами с величинами полей 310, 280, 260, 247 и 235 кЭ. Катионы в такой структуре имеют соответственно 0, 1, 2, 3 и 4 вакансии во второй координационной сфере. Очевидно, что при высоких температурах заселенности позиций приближаются к случайному закону распределения, что соответствует полному разупорядочению вакансий в структуре.

Вычисление заселенности позиций в начальном состоянии закаленных образцов дает значения N0 = 0,31; N1 = 0,20; N2 = 0,34; N3 = 0,11; N4 = 0,05. Таким образом, наблюдается отклонение распределения вакансий от случайного зако- на, так как нулевая намагниченность возможна только при случайном законе распределения вакансий. Следовательно, у образцов в начальном состоянии есть упорядочение вакансий и намагниченность этих образцов должна быть отличной от нулевой.

Оценка заселенностей проводилась по анализу относительной интенсивности секступлетов, на которые разлагался экспериментальный спектр ЯГР. Эти заселенности сравнивались с величинами, ожидаемыми для случайного закона распределения.

Для объяснения наблюдаемой нулевой намагниченности при некоторой упорядоченности вакансий в структуре необходим анализ величины и знака локального поля на некотором узле кристаллической решетки с различным расположением вакансий в структуре.

Магнитные свойства системы можно описывать гейзенберговским гамильтонианом [1–4; 6–8]

H = -X IfmSfSm, jm где f, m – узлы кристаллической решетки; Ifm – обменные параметры; Sf – оператор спина на узле f.

В общем случае обменное взаимодействие может быть дальнодействующим и осциллирующим (механизм РККИ). Ограничимся рассмотрением случая, когда I fm отличны от нуля только для ближайших соседей. В простейшем случае обменные параметры принимают только два значения: I 22 – между базисными плоскостями и I 11 – внутри плоскости.

Если ограничиться случаем рассмотрения изинговской части гамильтониана

Н = ^- X ¹ fm ° f ° . .

fm где <5 f = 2 Sf, то собственные значения парциальных собственных функций [1–4; 6–8]

Фm Н)=[п|Т)а П|Ф ), ] αβ

n гамильтониана Н0 можно записать в виде w. =-^х 1,. (ф . if .1 ф n)=-1 х f °';)° m'.

4 fm                      4 fm

По условию минимума энергии W ? = min ( W . ) получим

W ? =-1 х « ? = ? .

4f где е0 = х 1mс. — локальное поле на узле f. m

Таким образом, необходимым условием минимума W 0 является g ? е ? > 0. по которому следует, что направление спина однозначно связано со знаком локального поля:

00 g f = sign е f .

Например. спин в узле f при е f = 0 является парамагнитным и может иметь любую ориентацию. Включение малого магнитного поля вдоль оси квантования снимает это вырождение и спин принимает значение с ? = 1.

В рамках рассматриваемой модели имеется конечное число типов локальных полей, характеризующихся различными типами распределения вакансий вокруг данного узла f (рис. 4).

Для кристаллической структуры типа NiAs (рис. 4, а) основное состояние спина на узле f, не содержащем вакансии в ближайшем окружении, имеет вид е? = 6111 - 2122 < 0.

Для расположения ионов железа в плоскости, перпендикулярной оси с (рис. 4, б ) характерно следующее: если в базисной плоскости, в которой находится рассматриваемый узел f , имеются вакансии, то основное состояние будет зависеть от их числа, однако знак локального поля при этом меняться не будет:

е ' = 5 1 11 - 2 1 22 < 0.

е ? =-2 1 22 < 0.

т. е. ε ⁰ _f последовательно принимает значения для 1, 2, …, 6 вакансий в ближайшем окружении.

Если вакансии находятся в соседних базисных плоскостях α, то локальное поле на узле f может принимать как положительное, так и отрицательное значение. Даже при соотношении 6 1 11 <  1 ₂₂. когда наличие одной вакансии не приводит к изменению знака у локального поля ε⁰ _f на узле f (рис. 4, в ), две вакансии, расположенные в плоскостях α, неизбежно должны вызвать переориентацию спина (рис. 4, г ). Основное состояние для первого случая будет иметь вид е ? = 6 1 11 - 1 ₂₂ <  0. для второго - е ? = 6 1 11 > ?. Если узел f окружен вакансиями и в плоскости α, и в плоскости β, то спин в этом случае будет находиться в парамагнитном состоянии (рис. 4, д ).

Рис. 4. Кристаллическая ( а , б ) и магнитная ( в , г , д ) структура пирротина с различным расположением вакансий в структуре железа:

x – ось квантования

Для объяснения кривой J / J 0 ( T ) метастабиль-ной фазы сульфида железа предположим, что в стабильном фазовом состоянии образец является ферримагнетиком. Суммарный магнитный момент подрешеток Μ = Μ β – М α отличен от нуля только при условии, что число вакансий на подрешетках различно. Для определенности будем считать, что число вакансий в четных базисных плоскостях больше, чем в нечетных плоскостях. Тогда М α >  Μ β , что соответствует упорядочению вакансий в четных базисных плоскостях. В результате закаливания можно получить некоторое неравновесное распределение вакансий, при котором часть спинов будет инвертирована. По предположению, число вакансий в стабильном фазовом состоянии больше в четных базисных плоскостях, поэтому число таких спинов будет больше в нечетных плоскостях. Следовательно, суммарный магнитный момент такого образца меньше, чем у исходного.

Итак, с учетом уменьшения числа вакансий в четных базисных плоскостях намагниченность может уменьшаться практически до нуля за счет их частичного разупорядочения при закаливании образца. В данном случае закон распределения вакансий отличен от случайного распределения, т. е. наблюдается частичное упорядочение вакансий в четных базисных плоскостях. После нагрева у закаленного образца намагниченность возраста- ет. Это происходит в результате активизации изменения направления спина и перераспределения вакансий в базисных плоскостях. Если образец не имеет инвертируемых спинов в кристаллической структуре, то намагниченность закаленных образцов отлична от нулевого значения.

Таким образом, у ферримагнитных сульфидов железа в метастабильном состоянии возможны изменения намагниченности практически до нуля. Эти изменения определяются перераспределением вакансий в базисных плоскостях кристаллической структуры и процессами переориентации спинов в зависимости от расположения катионных вакансий во второй координационной сфере. Описанная выше модель качественно объясняет это магнитное превращение.