Филлотаксис: расположение листьев на горизонтальной ветке и кристаллографические бордюры

Voytekhovsky, Yu. L. et al. 2024. Phyllotaxis: Leaf arrangement on a horizontal branch and crystallographic borders. Vestnik of MSTU, 27(2), pp. 119–125. (In Russ.) DOI:

Филлотаксис – упорядоченное расположение листьев на стеблях и ветках растений. На такое расположение листьев с давних пор обращали внимание наблюдательные ученые. В привычной нам научной форме одним из первых его пытался описать Леонардо да Винчи на рубеже XV–XVI вв. И. Кеплер в 1611 г. упоминает его в сочинении "О шестиугольных снежинках" ( Кеплер, 1982 ). Ш. Бонне в 1754 г. обнаружил в спиральном филлотаксисе некоторых растений золотое сечение. А. Браун в 1830 г. и К. Ф. Шимпер в 1835 г. предприняли систематические измерения. А братья Огюст и Луи Браве в 1837 г. не только связали спиральный филлотаксис с числовыми рядами Фибоначчи, но сформулировали и доказали ряд теорем. В ходе поисков адекватной формы математического описания филлотаксиса ботаники обратили внимание на достижения развивавшейся науки о геометрически правильных формах кристаллов. О. Браве в 1848 г. вывел 14 типов кристаллических решеток (решеток Браве) – фундаментальный результат, описывающий трансляционное упорядочение элементарных ячеек в структуре кристаллов ( Браве, 1974 ).

Естественное объяснение филлотаксиса состоит в том, что каждый вид растения, исходя из условий обитания, в ходе эволюции решал задачу оптимизации светового потока и обеспечения фотосинтеза в каждом листе. Найденный оптимум закреплялся в генотипе и становился видовым фенотипическим признаком. (На феноменологическом уровне локальный энергетический оптимум в расположении атомов также транслируется по всему кристаллу.) В научном исследовании этот признак нужно зафиксировать с достоверностью, допускающей малые флуктуации, присущие формам растений под влиянием среды. Но на практике до сих пор используются вербальные описания прирастаний листьев на стебле и ветке: очередное, супротивное, кососупротивное, кольчатое, мутовчатое и т. д. ( Горянинов, 1841; Ванин, 1967; Иллюстрированный определитель…., 2006; Атлас…, 2010; Шишкин, 2020; Пескова, 2022 ). Если винтовой филлотаксис на стебле описывается с использованием указанной выше математической теории (по сути, сводящейся к винтовым осям разрешенных и запрещенных в кристаллографии рациональных и даже иррациональных порядков), то для листьев на горизонтальной ветке дело заканчивается применением только вербального описания. Между тем для этого случая целесообразно использовать теорию кристаллографических бордюров.

В настоящем исследовании рассматривается описание расположения листьев на горизонтальной ветке и на вертикальном стебле с применением в первом случае теории кристаллографических бордюров, во втором – теории винтовых осей.

Кристаллографические бордюры

В кристаллографии бордюром называется линейно упорядоченный (ритмично повторяющийся) односторонний орнамент ( Шубников, 1940; Вайнштейн, 1979 ). Каждый бордюр состоит из одинаковых кластеров, полученных из асимметричного элемента одной или несколькими операциями симметрии, совместимыми с односторонней полосой: продольной плоскостью Р, поперечными плоскостями П, центрами инверсии С на их пересечении, конечной трансляцией Т и плоскостью скользящего отражения Т* (композицией Т и отражения в Р на половине шага трансляции). Теория сводится к тому, чтобы исходный асимметричный элемент размножить в бордюр всеми возможными комбинациями указанных операций. В двух простейших случаях исходный элемент порождает бордюры операциями Т и Т*. Доказано, что возможны бордюры всего 7 типов (рис. 1, а ).

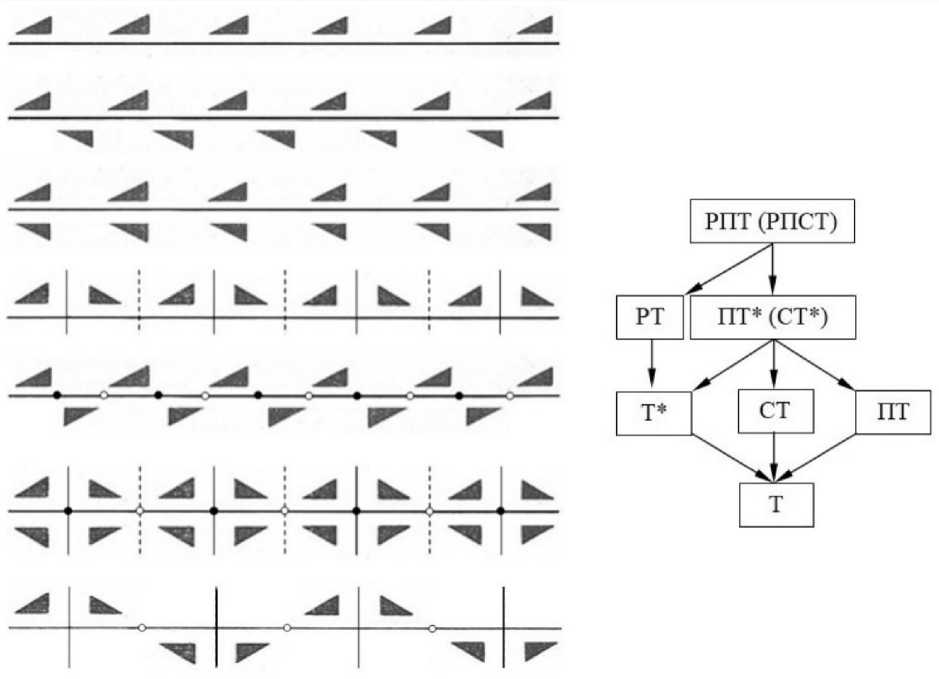
Данный факт может показаться невероятным ввиду огромного разнообразия линейных орнаментов, окружающих нас в природе и дизайне. Но причина кроется в устройстве исходного элемента, по традиции обозначенного на рис. 1 асимметричным треугольником. Сплошными линиями на рис. 1 показаны направление трансляции Т, совпадающий с ним след Р и плоскости П в кластере; штрихами – дополнительные плоскости П, появляющиеся между кластерами в силу геометрических теорем. Черными кружками показаны центры инверсии С в кластерах, белыми – дополнительные центры инверсии между ними. Каждый бордюр содержит минимально достаточный или полный список операций симметрии ( Войтеховский, 2020 ).

Наборы элементов симметрии в бордюрах соподчинены нетривиальным образом (рис. 1, б). Соподчинение легко установить при сравнении названий. Следует иметь в виду, что операция Т входит в Т*, а Т* – в композицию РТ. По стрелкам от высшей группы симметрии РПТ (полное название РПСТ, центр инверсии С появляется автоматически на пересечении Р и П; аналогично, бордюр ПТ* имеет второе название СТ*) можно разными путями спуститься к низшей группе Т – самой простой в схеме, но в математическом смысле нетривиальной. Иерархия подгрупп любой математической группы (в нашем случае – группы симметрии) должна завершаться тривиальной группой Е (ничего не меняющей, подобно 1 при умножении чисел). В нашем случае она отвечает не бордюру, а любому неупорядоченному узору. Необходимо указать на это обстоятельство потому, что оно имеет очевидную ботаническую интерпретацию – незакономерное (не отвечающее ни одному из бордюров, представленных на рис. 1) расположение листьев на ветке.

б

а

Рис. 1. Типы бордюров ( а ; сверху вниз): Т, Т*, РТ, ПТ, СТ, РПТ(РПСТ), ПТ*(СТ*); иерархия групп симметрии бордюров ( б )

Fig. 1. а – 7 types of borders (from top to bottom): Т, Т*, РТ, ПТ, СТ, РПТ(РПСТ), ПТ*(СТ*); б – hierarchy of border symmetry groups

Ботанические бордюры

Кристаллографические бордюры – односторонние орнаменты. Именно это позволяет использовать их для описания ритмичных расположений листьев (у которых верхняя, т. е. обращенная к солнцу, сторона радикально отлична от нижней) на горизонтальной ветке, когда все они условно лежат в одной плоскости. Но и здесь возможны варианты: (1) лист прирастает косо к ветке по ходу ее роста, и тогда неважно, он симметричен или асимметричен; (2) лист ортогонален к ветке, и тогда важно, он симметричен (2а) или асимметричен (2б). Случай (1) согласуется с бордюрами Т, Т* и РТ (рис. 2). (Черным цветом показан лист, с которого начинается построение бордюра.) Другие варианты противоречивы – в них правильное прирастание листа сочетается с обратным. В случае (2а) лист состоит из двух асимметричных половинок, связанных плоскостью П, и с точки зрения теории кристаллографических бордюров должен рассматриваться как кластер. Он сочетается с бордюрами ПТ, ПТ*, СТ и РПТ (рис. 3). Бордюры ПТ* и СТ очень похожи. Но в ПТ* каждый нижний/верхний лист прирастает строго посередине (между верхними/нижними). В СТ кластер из двух противоположно ориентированных листьев транслируется на некоторый (произвольный) шаг. Случай (2б) с точки зрения симметрии сводится к случаю (1).

На рис. 1, б показано, что бордюры различаются по степени симметричности, обычно сопоставляемой с совершенством организации. Но если в кристаллографии это не привносит смысловых искажений, то в ботанике может быть рискованно, а то и недопустимо. Эволюционные стратегии современных растений столь сложны, что, скорее всего, их морфологию нельзя выстраивать на восходящей лестнице совершенства, ориентируясь только на симметрию расположения листьев. Очевидное и, пожалуй, достаточное применение предлагаемого подхода – фиксация таких расположений, если они существуют, в рамках строгой конечной систематики.

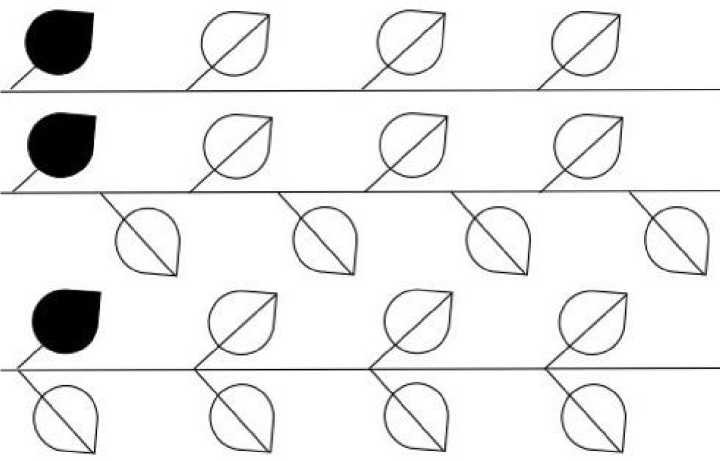
Рис. 2. Симметричный лист, косое соединение с веткой: (сверху вниз) Т, Т* и РТ

Fig. 2. Symmetrical leaf, obliquely connection to the branch. From top to bottom: Т, Т*, and РТ

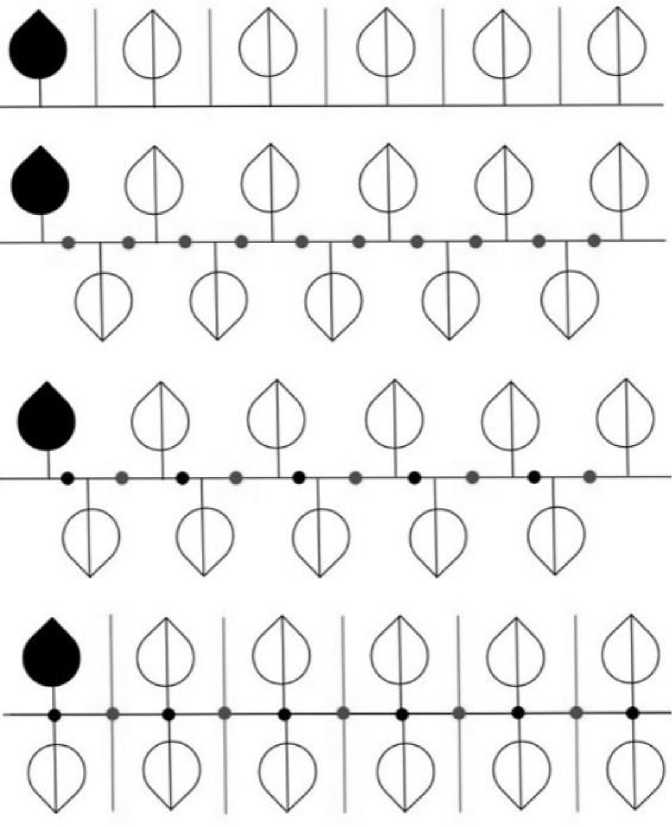
Рис. 3. Симметричный лист, ортогональное соединение с веткой: (сверху вниз) ПТ, ПТ*, СТ и РПТ Fig. 3. Symmetrical leaf, orthogonal connection to the branch. From top to bottom: ПТ, ПТ*, СТ and РПТ

Реальные прототипы

Оказался несложным поиск реальных прототипов всех ботанических бордюров в парках и ботанических садах Санкт-Петербурга (рис. 4, 5). Заметим, что у хамедореи Зейфрица (рис. 4) за элемент повторяемости объективно следует принять пару листьев, близко прирастающих по разные стороны ветки, но всегда разделенных небольшим интервалом. Более сложная интерпретация состоит в том, чтобы допустить, что изначально листья растут ортогонально ветке (бордюр СТ, рис. 3) и наклоняются к ней по мере роста. Вопрос следует изучить дополнительно. Но весьма показательно и интересно, что точная фиксация ситуации сразу породила вопрос об онтогенезе растения. У вербеника монетного (рис. 5) тип бордюра ПТ принят на том основании, что его мутовки из двух листьев ориентированы всегда вверх и обладают внутренней симметрией, но может быть оспорен. О частоте разных бордюров в мире растений говорить рано. По нашим наблюдениям, тип ПТ наиболее редок, что и не позволило привести более убедительный пример.

Рис. 4. Косое прирастание: (фото автора; слева направо) T – хамедорея Chamaedorea seifrizii ; T* – кизильник Cotoneáster sp .; PT – церцидифиллюм Cercidiphyllum japonicum

Fig. 4. Obliquely connection, from left to right: Т – Chamaedorea seifrizii ;

Т* – Cotoneáster sp .; РТ – Cercidiphyllum japonicum

Рис. 5. Ортогональное прирастание: (фото автора; слева направо) ПТ – вербеник Lysimachia nummularia ; ПТ* – кочедыжник Athyrium filix-femina ;

СТ – замиокулькас Zamioculcas zamiifolia ; РПТ – вика Vicia sepium Fig. 5. Оrthogonal connection, from left to right: ПТ – Lysimachia nummularia ; ПТ* – Athyrium filix-femina ; СТ – Zamioculcas zamiifolia ; РПТ – Vicia sepium

Заключение

Для описания расположений листьев на условно горизонтальной ветке непротиворечивыми оказались все типы кристаллографических бордюров. При этом удобная номенклатура по порождающим операциям симметрии однозначно фиксирует ортогональное прирастание симметричного листа (ПТ, СТ, РПТ, ПТ*) или косое – симметричного и асимметричного листа (Т, Т*, РТ). Сбой периодичности в расположении листьев по шагу трансляции Т или отсутствие листа в нужном месте бордюра (если это представляется принципиально важным, а не флуктуацией) должны означать, что природа избрала другой путь рациональности для достижения своей цели – оптимизации светового потока для каждого листа. Этот тип организации выше отмечен как тривиальная группа симметрии. Все варианты ботанических бордюров установлены авторами в природе.

Выше неявно предполагалось, что листья вдоль ветки имеют одинаковый размер. Это в общем не так – в направлении роста ветки их размер уменьшается. И тогда для описания целесообразно применить симметрию подобия ( Шубников, 1960 ). Плоскость симметрии листа, косо ориентированного к ветке, можно рассмотреть как плоскость гомологии ( Михеев, 1961 ). Листья на дугообразной ветке можно описать в терминах криволинейной симметрии ( Наливкин, 1925, 1951; Падуров, 1926; Шафрановский, 1979 ). Для описания расположений листьев на стеблях следует использовать (по сути, уже используются) винтовые оси. Современная кристаллография предоставляет для этого стройную теорию ( Вайнштейн, 1979 ). Наконец, вместо одного листа природа предлагает разнообразные кластеры-мутовки (соцветия, несколько листьев, лист с иглой и т. д.). Считать их элементами бордюра или относить такую организацию к тривиальной группе симметрии – вопрос открытый. В последнем случае важно понять, как природа решила задачу оптимизации светового потока, избежав в расположении листьев кристаллографического порядка.