Фильтрация натурных данных для численного моделирования трехмерных турбулентных течений с применением подхода LES

В прибрежных системах велика роль вертикального турбулентного обмена. В ряде случаев он определяет транспорт биогенных веществ, от него зависит насыщенность водной среды кислородом, а также возникновение заморных явлений при отсутствии турбулентного перемешивания в водной толще. Задание коэффициента вертикального турбулентного обмена в виде константы приводит к искаженной картине распределения скоростей водной среды, а также концентраций биогенных веществ и кислорода по вертикальному направлению и не обеспечивает требуемую точность расчета 3D-течений, что подтверждается сравнением результатов численного моделирования и непосредственно измерений 3D-вектора скоростей водной среды при помощи оборудования типа ADCP (Acoustic Doppler Current Profiler).

Трехмерный характер течения, стохастическая природа и широкий пространственновременной спектр турбулентности делает предсказательное моделирование характеристик сложных турбулентных течений сложной и трудоемкой задачей. Исходная предпосылка математического моделирования турбулентных течений в рамках феноменологического подхода состоит в предположении о приемлемости уравнений Навье–Стокса для интерпретации турбулентных течений и предсказания их мгновенных характеристик.

Существует необходимость расчета вертикальной структуры течения для решения ряда прикладных задач, в первую очередь антропогенного загрязнения акваторий, а также оценки надежности гидротехнических сооружений – защитных конструкций, нефтяных платформ, волнопре-

Сухинов А.И., Проценко С.В., Фильтрация натурных данных для численного моделирования Проценко Е.А. трехмерных турбулентных течений с применением подхода LES образователей и других устройств, установленных в районах шельфовой зоны и мелководных морях, при наложении эффектов прилива и штормового нагона [1].

Несмотря на проведение широкого круга исследований, ориентированных на рассматриваемую проблему, в них не была достаточно полно отражена вся совокупность разнообразных факторов и процессов, влияющих на структуру и параметры вертикального турбулентного перемешивания [2–4]. Это указывает на необходимость проведения системного анализа проблемы и построения взаимосвязанного комплекса моделей, высокопроизводительных алгоритмов и программ. Относительно небольшое число публикаций, посвященных моделированию разномасштабного вертикального турбулентного перемешивания и сложность получения натурных данных в реальной области, свидетельствует о необходимости привлечения развитых в авторском коллективе 3D моделей гидродинамики, которые учитывают специфику прибрежных систем, и обладают, по сравнению с известными моделями, лучшей точностью и повышенным запасом устойчивости, при перепадах глубин в 15–20 раз. Проведенный обзор существующих на сегодняшний день математических моделей гидродинамики показал, что для расчета гидродинамической составляющей используется гидростатическое приближение, такой подход не позволяет учитывать ускорение движения водного потока по вертикальной составляющей. При параметризации моделей турбулентного перемешивания широко используются упрощенные функциональные зависимости, не связанные с реалистическими моделями гидрофизики, что приводит к моделям, не обладающих должной прогностической ценностью. Немногие из работ посвящены параллельной численной реализации задач данного класса. Несмотря на большое количество существующих программных комплексов, позволяющих моделировать гидродинамические процессы: POM (Princeton Ocean Model), EFDC (The Environmental Fluid Dynamics Code), DELFT, Mars3D, CARDINAL (Coastal Area Dynamics Investigation Algorithm, ветро-волновые модели третьего поколения WAM, SWAN (Simulation Waves Nearshore), WaveWatch, данные разработки обладают рядом существенных недостатков [5–8]. Проведенный анализ этих и других моделей показывает, что подавляющее большинство имеющийся подходов к построению моделей гидродинамических процессов в прибрежной зоне мелководных водоемов основывается на приближении мелкой воды, или в лучшем случае на гидростатическом приближении, которое не учитывает турбулентный тепломассообмен по вертикальному направлению. С другой стороны, имеющиеся опытные данные свидетельствуют о существенном влиянии этих процессов на гидрофизику береговой зоны, дислокацию солей и газовый режим. Поэтому построение, изучение и применение пространственно-трехмерных моделей гидродинамики, предусматривающих механизмы турбулентного обмена по вертикальной координате, представляется актуальной научной и важной прикладной проблемой.

Среди основных методов численного моделирования трехмерных турбулентных течений необходимо выделить прямое численное моделирование (Direct Numerical Simulation, DNS), моделирование крупных вихрей (Large Eddy Simulation, LES) и решение осредненных по Рейнольдсу уравнений Навье–Стокса (Reynolds Averaged Navier-Stokes equations, RANS). Имеются также различные промежуточные подходы, сочетающие в себе те или иные черты RANS, LES и DNS, например, метод моделирования отсоединенных вихрей (Detached Eddy Simulation, DES) [9].

Прямое численное моделирование (DNS) предполагает численное решение полных нестационарных трехмерных уравнений Навье–Стокса. При таком подходе разрешаются все масштабы турбулентного движения. Для использования DNS требуются мощные вычислительные ресурсы, а возможности его применения ограничиваются расчетами течений с простой геометрией и малыми числами Рейнольдса.

Использование осредненных по Рейнольдсу уравнений Навье–Стокса (RANS) требует намного меньших вычислительных ресурсов. Данный подход успешно применяется в практических расчетах. Однако используемые для замыкания уравнений Рейнольдса модели турбулентности не обладают приемлемой универсальностью, а потому не могут применяться для решения широкого круга прикладных задач.

Метод моделирования крупных вихрей (LES) является компромиссным вариантом между DNS и решением RANS. Данный подход ограничивается исследованием течений только в масштабах, превышающих некоторую заданную величину. В методе LES осуществляется решение фильтрованных по пространству уравнений Навье–Стокса, и разрешается движение только крупных вихрей. Мелкие вихри имеют более универсальную структуру и моделируются при помощи моделей подсеточного масштаба (Subgrid Scale Model, SGS), построенных на основе концепции вихревой вязкости или других рациональных приближений процессов переноса.

Метод моделирования крупных вихрей (LES) основан на двух предположениях. Одно из них состоит в возможности разделения поля течения на движение крупных и мелких вихрей. Крупные вихри, находящиеся под прямым воздействием граничных условий и несущие в себе максимум рейнольдсовых напряжений, рассчитываются. Мелкомасштабная турбулентность считается изотропной и имеющей универсальные характеристики, а потому менее критичной и более поддающейся моделированию. Другое предположение заключается в возможности аппроксимации нелинейных взаимодействий между крупными и мелкими вихрями только по крупным вихрям с использованием подсеточных моделей (SGS). Иначе говоря, принимается гипотеза о статистической независимости крупных и мелких вихрей.

В то время как DNS отображает весь диапазон размеров вихрей, метод LES считает наиболее важными крупные вихри, соответствующие малым волновым числам. При этом подсеточные модели не оказывают критического влияния на результаты в целом. Статистика крупных вихрей обычно не чувствительна к подсеточному моделированию. Крупномасштабное движение рассчитывается путем решения фильтрованной системы уравнений Навье–Стокса, которую формально можно записать в таком же виде, что и систему уравнений Рейнольдса. Роль подсеточного моделирования возрастает при увеличении числа Рейнольдса.

Мелкомасштабное движение исключается из уравнений Навье–Стокса при помощи применения операции фильтрации и моделируется с использованием подсеточных моделей. Среди наиболее популярных и часто используемых фильтрующих функций можно отметить фильтры Гаусса и Фурье, а также коробочный фильтр (boxfilter). При проведении расчетов на основе метода контрольного объема фильтрация осуществляется в результате интегрирования дифференциальных уравнений, представляющих законы сохранения, по контрольным объемам разностной сетки. Классификация подсеточных моделей проводится по тем же признакам, что и в RANS (по числу соотношений, вводимых в дополнение к системе фильтрованных уравнений) [10-11].

Результаты расчетов, полученные при помощи LES, зависят от ширины фильтра Δ, которая входит в оператор фильтрации и обычно связывается с размером шага разностной сетки. Уменьшение ширины фильтра позволяет воспроизвести более широкий частотный диапазон флуктуаций решения. Увеличение Δ способствует сглаживанию решения, а при Δ→0 метод LES переходит в DNS. Тем не менее метод LES является перспективным направлением в развитии методов расчета турбулентных течений и представляется весомой альтернативой DNS и RANS.

Выбор оператора фильтрации

Для получения фильтрованных уравнений Навье–Стокса используются подходы с явным и неявным введением оператора фильтрации.

Введем обобщенный фильтр, дающий формальное определение операции осреднения и позволяющий исключить из рассмотрения масштабы, меньшие некоторой наперед заданной величины Δ, называемой шириной фильтра (filter length). Вихри, размер которых меньше, чем ширина фильтра, не разрешаются. Обобщенный фильтр определяется следующим образом:

f ( x , t ) = J f ( i , t ) g ( x , i , A ) d i .

D

В том случае, когда функция g(x, i) зависит только от разности x - i, операции дифференцирования и фильтрации коммутируют. Тогда обобщенный фильтр вводится как интеграл свертки f (x ’ t) = L f (i ’ t) 8 (x - i ’ A) di = f (x ’ t)' g (x ’ A).

Предполагается, что фильтрующая функция g ( x ) (filtering function), называемая также ядром фильтра (filter kernel), является четной и бесконечно дифференцируемой в ограниченной области D , имеет компактный носитель и удовлетворяет условию нормировки

g(x) = g(-x), J g(i, А№ = 1- d

Сухинов А.И., Проценко С.В.,       Фильтрация натурных данных для численного моделирования

Проценко Е.А.                трехмерных турбулентных течений с применением подхода LES

В предельном случае имеют место соотношения lim j f(^, t)g(x - ^, Д)d^ = f (x, t),  lim g(x, Д) = S(x).

Д^даJ                                Д^да

D

Интегрирование проводится по всей области течения D. Фильтрующая функция определяет структуру и размер мелкомасштабных турбулентных вихрей, разрешаемых системой осреднен-ных уравнений.

Согласно теореме Бореля о свертке, преобразование Фурье свертки равняется произведению преобразований Фурье ^[ f ( x , t ) • g ( x ) ] = ^[ f ( x , t ) ]^[ g ( x ) ] •

Преобразованием Фурье функции f ( x ), абсолютная величина | f ( x )| которой интегрируема

+да на интервале -да < x < + да, называется функция c(k) = ^[ f (x)], где c(k) = J f (x)exp(-ikx)dx.

-да

+да

Формула обращения имеет вид f ( x ) = J c ( k )exp( i kx ) d k .

-да

Существуют различные виды фильтров, примеры некоторых из них.

используемые в численных расчетах. Приведем

Коробочный фильтр g ( x - £ ) = <

1/ Д ³,

0,

I ^x i ^- ^ i\ ^^Л * i ^/2

I xi- £| >Д xi/2

•

Фильтр Гаусса g ( x - £ ) =

\ 3/2

П Д2 ;

exp

-6| x - £ |²/ Д ² •

r        1 T-T^sin2 ^ e * - §

•

Фильтр Фурье g ( x - ^ ) = —- П —, Si = n -^L-—^L Д i S         ^Д

За исключением Фурье-фильтра (sharp Fourier cutoff filter), фильтрация отличается от стандартной операции осреднения во времени тем, что f ^ f .

Для представления наименьших разрешимых масштабов необходимо, чтобы ширина фильтра не превосходила шага разностной сетки. Обычно различие между этими двумя величинами игнорируется, и ширина фильтра полагается равной Д = V ^1/3 = ( Д х Д y Д ) ^1/3, где V - объем ячейки разностной сетки; Д х , Д у , Д z - шаги сетки в координатных направлениях x, у и z соответственно. Поскольку ширина фильтра зависит от разностной сетки, то фильтрующую функцию часто называют сеточным фильтром (grid filter).

Для расчета пограничных слоев предлагается заменить шаг сетки в нормальном к стенке направлении Д у на величину Д у и находить ширину фильтра, используя соотношение

/     .      X1/3

Д = ( Д х Д у Д z )   .

Причем Д у = Д у вблизи стенки и Д у = Д у вдали от стенки. Для промежуточных значений у используется плавный переход между указанными предельными значениями. Величина Д у представляет собой среднее значение Д у в пристеночной области, а величина Д у рассчитывается по формуле

ДУ =

Л 3

ДУ )

г)VДу J

-I - 1/3

•

Имеются также и другие определения ширины фильтра

N

Д=eN П^i

V i = 1

f 2     f N

,Д = p ^A*2

V г = 1

X1/2

, Д = в min Д х у, Д= В max Д х _z, i =1,..., N                 i =1,..., N

где N – размерность задачи, β – коэффициент пропорциональности.

При фильтрации уравнений Навье–Стокса фильтрующая функция выбирается таким образом, чтобы выполнялось условие ( g * , V ) и = 0.

Форма записи уравнений, используемых в LES, не зависит от того или иного выбора фильтрующей функции g ( x ). Конкретный вид фильтра играет роль только при статистической обработке и сравнении результатов численного моделирования с экспериментальными данными или результатами, полученными при помощи DNS. В то же время результаты численных расчетов, в частности размеры разрешимых масштабов турбулентности зависят от выбора ширины фильтра. Приемлемая ширина фильтра выбирается, как правило, методом проб и ошибок. При Δ→0 метод LES переходит в DNS.

Интерес к турбулентности в мелководных водоемах, типа Азовского моря, вызван тем, что в местах ее существования происходит интенсивная передача количества движения и тепла, распространение пассивных примесей, перенос взвешенных частиц. Эти процессы существенно влияют на формирование и пространственную структуру физических, химических и биологических полей водоемов и их пространственные и временные изменения. Обработка собранного эмпирического материала ведется в настоящее время для изучения внутренней структуры зафиксированных возмущений мелкомасштабной турбулентности, определения скорости диссипации энергии возмущений [12].

Для оценок характеристик турбулентности с помощью прямых методов существует проблема, связанная с необходимостью получения больших объемов данных, а также длительных и дорогостоящих экспедиционных измерений.

Натурные данные получены в ходе экспедиции в Центрально-Восточной части Азовского моря и в Таганрогском заливе на НИС «Денеб» Южного научного центра РАН. Для измерения трехмерного вектора скорости движения водной среды использовался гидрофизический ADCP-зонд Workhorse Sentinel 600. Исследования проводились на 17 станциях. Измерения поля течений водного потока в Азовском море проводились по вертикали, начиная от ближней зоны чувствительности ADCP-зонда до дна. Измерения фиксировались с интервалом в 1 с каждые 10 см на измеряемой глубине. Скорость записывалась в соответствующий файл в мм/с. По столбцам приведены значения времени на часах прибора и 128 измерений по глубине одной из компонент вектора скорости в текущий момент времени. В описываемом эксперименте сохранение данных происходило по трем компонентам вектора скорости водного потока в текущий момент времени. Таким образом, при разрешении по вертикали в 10 см, и шаге по времени в 1 с для временного интервала 20–30 мин, имеется более 3 000 000 исходных измерений, в каждой точке (на каждой станции, которых 17) – более 150 000 (рис.1).

Экспедиции проводились с целью получения данных для накопления информации о состоянии и изменении гидрофизических и гидрохимических параметров. В рейсах проводилось исследование следующих измеряемых параметров: пульсации компонент скорости; погрешность измерения; глубина водоема в месте измерения; значение ветра. В мелководных водоемах плотностная стратификация отсутствует, процессы в вертикальном направлении носят существенно нелинейный характер, поэтому приходится прибегать к нестандартному третьему методу измерения и оценки коэффициента вертикальной турбулентной вязкости, основывающемуся на вычислении градиента средней скорости потока.

Рассмотрим применение различных фильтров для обработки мгновенных скоростей водного потока, полученных при измерениях. Будем использовать коробочный фильтр, фильтр Гаусса и фильтр Фурье при различной величине ширины фильтра. В данных расчетах ширина фильтра задавалась, исходя из размерности решаемой задачи гидродинамики и соответствующего данной размерности масштаба сетки.

Сухинов А.И., Проценко С.В.,       Фильтрация натурных данных для численного моделирования

Проценко Е.А.                трехмерных турбулентных течений с применением подхода LES

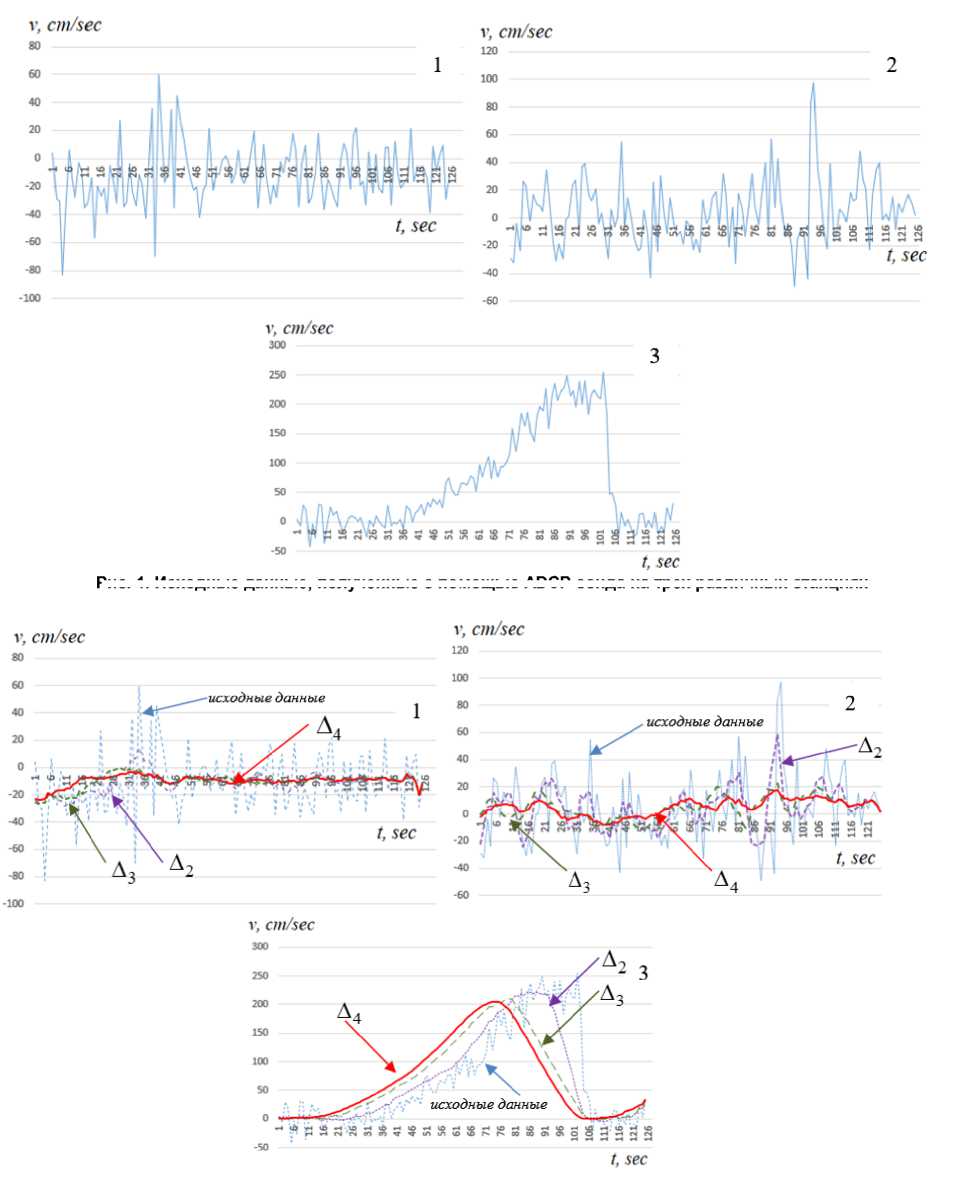
Рис. 2. Применение 1 – коробочного фильтра, 2 – фильтра Гаусса, 3– фильтра Фурье, при различной величине ширины фильтра: А₄ <  А₃ <  А₂

Рис. 2 демонстрирует пример работы программы, предназначенной для устранения зашумленности измеренных экспедиционных данных поля скорости водного потока. Процедура фильтрации заметно снижает разброс данных и амплитуду колебаний, что в свою очередь позволяет более адекватно оценивать информацию, полученную в ходе натурных экспериментов. Наличие погрешностей в измерениях пульсаций вертикальной компоненты скорости является одной из трудноразрешимых проблем и связанно со многими явлениями, происходящими в момент измерения, такими как девиация судна, колебания свободной поверхности, изменения глубины, устойчивости, ветра и волнения.

Рис. 1. Исходные данные, полученные с помощью ADCP-зонда на трех различных станциях

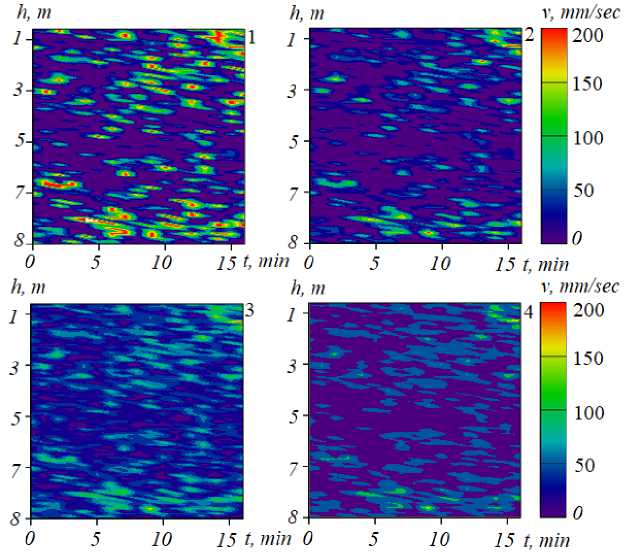
Рис. 3. Применение коробочного фильтра: 1 – исходные данные, 2, 3, 4 – данные, полученные с помощью фильтрации, при различной величине ширины фильтра: А4 < А3 < А2

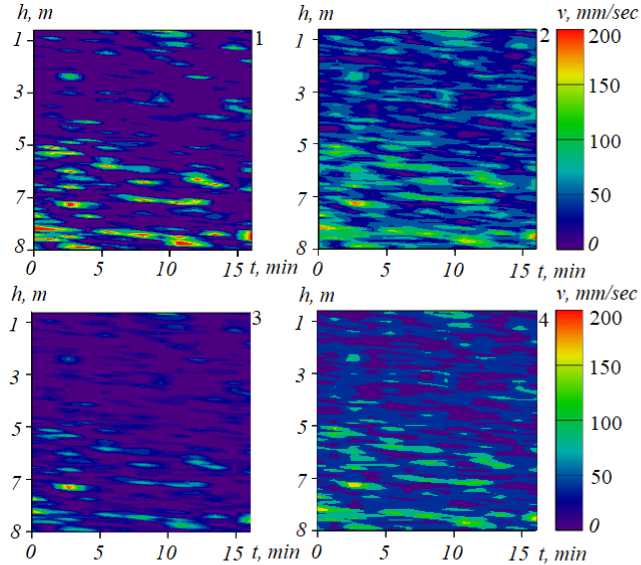
Рис. 4. Применение фильтра Гаусса: 1 – исходные данные, 2, 3, 4 – данные, полученные с помощью фильтрации, при различной величине ширины фильтра: А4 < А3 < А2

Сухинов А.И., Проценко С.В.,       Фильтрация натурных данных для численного моделирования

Проценко Е.А.                трехмерных турбулентных течений с применением подхода LES

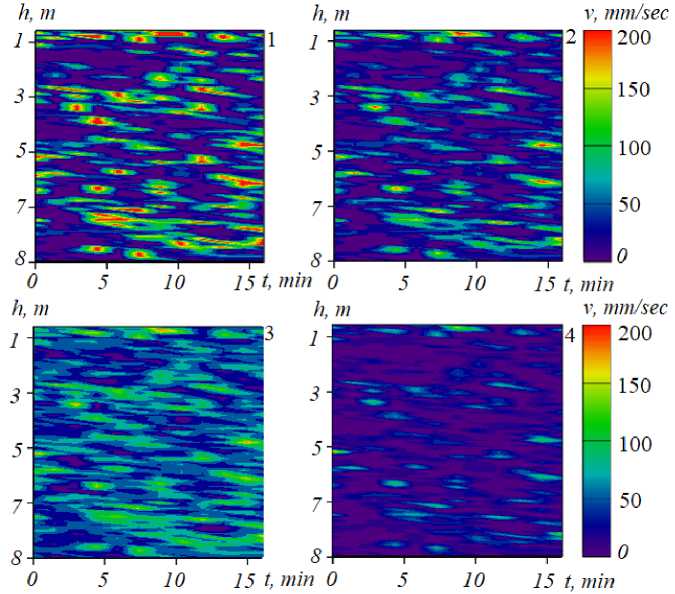
Рис. 5. Применение фильтра Фурье: 1 – исходные данные, 2, 3, 4 – данные, полученные с помощью фильтрации, при различной величине ширины фильтра: А4 < А3 < А2

Рис. 3–5 демонстрируют результат работы программного обеспечения, предназначенного для устранения зашумленности экспедиционных измерений, на примере одной из составляющих вектора скорости водного потока в двумерном случае. Цветом выделена скорость водного потока в мм/с в соответствии с приведенной цветовой шкалой.

Параметризация процесса турбулентного обмена в дискретных моделях в первую очередь для вертикального координатного направления выполняется с учетом градиента плотности водной среды на основе современных подсеточных моделей.

Для параметризации коэффициента вертикального турбулентного обмена рассмотрены алгебраические подсеточные модели, основанные на определении турбулентных потоков как ос-редненных по пространству или времени произведений отклонений составляющих скорости течений и переносимой физической величины. Были выполнены эксперименты на основе нескольких подходов для вычисления коэффициента турбулентного обмена по вертикали: параметризация Белоцерковского, Буссинеска, Смагоринского (рис. 6). Использовались отфильтрованные данные о распределении трехмерного вектора мгновенной скорости водного потока для глубин от 0,8 до 20 м и более, полученные при помощи ADCP WHS 600 WHS 1200 Sentinel.

Все методы параметризации коэффициента вертикального турбулентного позволяют в большинстве случаев получить схожие распределения коэффициента вертикального турбулентного обмена по порядку величины и локализации максимумов-минимумов.

Явление резких скачков коэффициента на всех графиках связано с погрешностями в измерениях пульсаций вертикальной компоненты скорости, которая входит в расчетную формулу метода. Наличие погрешностей в измерениях пульсаций вертикальной компоненты скорости связанно со многими явлениями, происходящими в момент измерения, такими как девиация судна, колебания свободной поверхности, изменения глубины, устойчивости, ветра и волнения.

Профили коэффициента вертикального турбулентного обмена в момент времени показывают, что параметризация Белоцерковского и Буссинеска наиболее адекватно отражает процессы турбулентного обмена именно для мелководных водоемов, но для оценки качества параметризации необходим более глубокий анализ с применением методов математической статистики.

0,04                                                                0,09 0,035                  *                                            °,08                         о 0,03                                                                °'07 0,025             jМ-------------------------- 0,06               * м               •                 *                °,05 0,02                  * •                0,04             •      •—♦----------ж— °-015                        .                                      0,03 0,01 :                .                                      °'02             : - . • ; 0,005            •                    .                        ПП1       •    *    • 0 1            f                                                1                                                    __________I____________ -0,005 ®--------2--------*--------6--------8--------™       0         2         4         6         8        10 ♦ SM ♦ BUS • BEL                                ♦ SM • BUS • BEL 0,06 -----------------1-----------------1-----------------1-----------------1-----------------1      0,08 0,05                                     .                           °'°7 0,06 °'04                                                                  0,05 0,03            -----—---------- •    -       •              0,04 ___                             •                      0,03 ------------- /            1 —-* 0,02                   •                            e                                 .    .                •          • :       ■    :                                 0,02                .     . ■ о            .     • °-01       2    .    '          •                                 0,01       •                      • 0                                    В                     0 02 468 10 0 2468 10 • SM ♦ BUS • BEL                                  • SM - ■•■ • BUS ♦ BEL 0,08 --------------1-------------r-------------1--------------1--------------1     0,05 0Д7             --A11-------                                   • °r°4      -------- -x о,об -----------/—n-----—                          0  • °'05                                                                   0,03 0,04                                                   -                                             /          \               e 0,03 ------------ / ,4. ’--- - •                 °'02 -------- / "pA------/ \t-- °'02             •    •    »          •    •    .                0,01       0    .    °    ’    .    1    ° 0,01         У ♦ О           •     ...     - 0--0 --- 02468 10 02468 10 ........ SM -•- BUS -•■ - BEL                                        -•- SM «-- BUS ♦ BEL 0,07                                                             0,035 0,06                             •                                0,03                 , 0,05                                                                   0,025 0,04                                                               0,02                                  *    * 0,03                             -                               0,015                                  *    *    • 0,02                                     о                             o,Ol 0,01      •    °    ° t         T 1 e              °-005      • ~ e         • o --------------------1111              о 0 2 468 10 02468 10 -e - SM -♦■ BUS • BEL                                   -♦- SM —♦- BUS -• BEL

Рис. 6. Коэффициент вертикального турбулентного обмена, рассчитанный на основе различных типов аппроксимаций для параметризации вертикального турбулентного перемешивания (по горизонтали – значения в м2/с)

Разработанное программное обеспечение позволило обработать большой объем данных натурных наблюдений движения и параметров водной среды в акватории Азовского моря, который был получен в ходе экспедиционных исследований с использованием гидрофизического зонда ADCP, с помощью процедуры фильтрации. Процедура фильтрации заметно снижает разброс данных и амплитуду колебаний, что в свою очередь позволяет более адекватно оценивать информацию, полученную в ходе натурных экспериментов.

Был применен коробочный фильтр, фильтр Гаусса и фильтр Фурье при различной величине ширины фильтра. В данных расчетах ширина фильтра задавалась, исходя из размерности решаемой задачи гидродинамики и соответствующего данной размерности масштаба сетки. Полученные данные планируется использовать для численного моделирования трехмерных турбулентных течений с применением подхода LES и сопоставления с результатами осреднения по RANS.

В статье рассмотрены возможности применения различных типов аппроксимаций для параметризации вертикального турбулентного обмена. С помощью ADCP-данных о пульсациях ско-

Сухинов А.И., Проценко С.В., Фильтрация натурных данных для численного моделирования Проценко Е.А. трехмерных турбулентных течений с применением подхода LES рости для нескольких станций измерения гидрологических характеристик проведен анализ результатов параметризации коэффициента вертикального турбулентного обмена. Все рассмотренные методы параметризации коэффициента вертикального турбулентного позволяют в большинстве случаев получить схожие распределения коэффициента вертикального турбулентного обмена по порядку величины и локализации максимумов-минимумов.

Исследование выполнено за счет гранта Российского научного фонда № 22-71-00015,

• 1.    Small Microplastics as a Main Contributor to Plastic Mass Balance in the North Atlantic Subtropical Gyre / M. Poulain, M.J. Mercier, L. Brach et al. // Environ. Sci. Technol. – 2019. – Vol. 53. – P. 1157–1164.

• 2.    Zippel, S.F. Turbulence from Breaking Surface Waves at a River Mouth / S.F. Zippel, J. Thomson, G. Farquharson // J. Phys. Oceanogr. – 2018. – Vol. 48. – P. 435–453.

• 3.    Stokes G.G. Supplement to a Paper on the Theory of Oscillatory Waves / G.G. Stokes // Mathematical and Physical Papers. – Cambridge University Press,1880. – Vol. 1. – P. 314–326.

• 4.    Smit, P.B. Nonlinear Wave Kinematics near the Ocean Surface / P.B. Smit, T.T. Janssen, T.H.C. Herbers // J. Phys. Oceanogr. – 2017. – Vol. 47. – P. 1657–1673.

• 5.    Material Transport in the Ocean Mixed Layer: Recent Developments Enabled by Large Eddy Simulations / M. Chamecki, T. Chor, D. Yang, C. Meneveau // Rev. Geophys. – 2019. – Vol. 57. – P. 1338–1371.

• 6.    DiBenedetto, M.H. Transport of Anisotropic Particles under Waves / M.H. DiBenedetto, N.T. Ouellette, J.R. Koseff // J. Fluid Mech. – 2018. – Vol. 837. – P. 320–340.

• 7.    Comparison Between Manta Trawl and in situ Pump Filtration Methods, and Guidance for Visual identification of Microplastics in Surface Waters / T.M. Karlsson, A. Kärrman, A. Rotander, M. Hassellöv // Environ. Sci. Pollut. Res. – 2019. – Vol. 27, Iss. 5. – P. 5559–5571.

• 8.    The Role of Ekman Currents, Geostrophy and Stokes Drift in the Accumulation of Floating Microplastic / V. Onink, D. Wichmann, P. Delandmeter, E. Van Sebille // J. Geophys. Res. Oceans. – 2019. – Vol. 124, no. 3. – P. 1474–1490.

• 9.    Methods for Sampling and Detection of Microplastics in Water and Sediment: a Critical Review / J.C. Prata, J.P. da Costa, A.C. Duarte, T. Rocha-Santos // Trends Anal. Chem. – 2019. – Vol. 110. – P. 150–159.

• 10.    Sukhinov, A.I. Long Waves Simulation in Coastal Systems Using Parallel Computational Technologies / A.I. Sukhinov, S.V. Protsenko // Young Scientist's Third International Workshop on Trends in Information Processing. – 2019. – Vol. 2500. – P. 1–10. http://ceur-ws.org/Vol-2500/paper_1.pdf

• 11.    Protsenko, S. Mathematical Modeling of Wave Processes and Transport of Bottom Materials in Coastal Water Areas Taking into Account Coastal Structures / S. Protsenko, T. Sukhinova // MATEC Web of Conferences, XIII International Scientific-Technical Conference “Dynamic of Technical Systems” (DTS-2017), Rostov-on-Don, Russian Federation. – September 13–15, 2017. – Vol. 132 (2017). – 04002.

• 12.    Zippel, S.F. Turbulence from Breaking Surface Waves at a River Mouth / S.F. Zippel, J. Thomson, G. Farquharson // J. Phys. Oceanogr. – 2018. – Vol. 48, Iss. 2. – P. 435–453.

Поступила в редакцию 6 сентября 2022 г.

FIELD DATA FILTERING FOR THE DIGITAL SIMULATIONOF THREE-DIMENSIONAL TURBULENT FLOWS USING THE LES APPROACH

A.I. Sukhinov1, S.V. Protsenko2, E.A. Protsenko2

• ¹    Don State Technical University, Rostov-on-Don, Russian Federation

• ²    Chekhov Taganrog Institute (branch) Rostov State University of Economics, Taganrog, Russian Federation

Сухинов А.И., Проценко С.В., Фильтрация натурных данных для численного моделирования Проценко Е.А. трехмерных турбулентных течений с применением подхода LES

Received September 6, 2022

Sukhinov Aleksandr Ivanovich is Corresponding Member of the Russian Academy of Sciences, Doctor of Physical and Mathematical Sciences, Professor, Head of the Mathematics and Computer Science Department, Don State Technical University, Rostov-on-Don, Russian Federation, e-mail: , ORCID iD:

Protsenko Sofya Vladimirovna is Candidate of Physical and Mathematical Sciences, Associate Professor of the Mathematics Department, Chekhov Taganrog Institute (branch) Rostov State University of Economics, Taganrog, Russian Federation, e-mail: , ORCID iD:

Protsenko Elena Anatol'evna is Candidate of Physical and Mathematical Sciences, Associate Professor of the Mathematics Department, Chekhov Taganrog Institute (branch) Rostov State University of Economics, Taganrog, Russian Federation, e-mail: , ORCID iD: