Фильтры нижних частот

Для фильтрации сигналов в электросвязи, измерительной технике, системах обработке сигналов, системах автоматического управления и т. д. широко используют фильтры различных принципов действия с различными характеристиками. В зависимости от диапазона частот, относящихся к полосе пропускания и полосе подавления, различают фильтры низкочастотные, высокочастотные, полосовые, режекторные (заграждающие) фильтры. Также применяются всепро-пускающие фильтры, которые обладают постоянной амплитудно-частотной характеристикой на требуемом диапазоне частот, при этом их фазочастотная характеристика представляет собой заданную функцию частоты.

Свойства используемых линейных фильтров могут быть описаны передаточной функцией. Составив передаточную функцию для одного типа фильтра, например фильтра нижних частот, используя метод подстановки, можно получить фильтры других типов.

Можно привести следующие подстановки:

– подстановка для преобразования фильтра нижних частот в фильтр верхних частот

ωср s = —-;

S 1

– подстановка для преобразования фильтра нижних частот в полосовой фильтр s = к

^s 2 + ^Ю ср .

Ю ср ^s 2 ’

– подстановка для преобразования фильтра нижних частот в режекторный фильтр

® ср ^s 3

s =-----~-----

• ^k ( s 32 +Ю 2р )’

здесь к = ю _ср / Аю , ю _ср - частота среза фильтра, Ato - полоса подавления для режекторных и полоса пропускания для полосовых фильтров.

Получить одни типы фильтров заданного порядка из других типов фильтров того же порядка можно путем замены элементов электрической цепи.

Линейные фильтры являются неидеальными, и, более того, их проектирование связано с компромиссом противоречивых требований.

В современной технической литературе рассматриваются фильтры Бесселя (Гаусса), Чебышева, Баттерворта, эллиптические фильтры, фильтр с критическим затуханием и другие. Все эти фильтры нижних частот в общем случае могут быть описаны передаточной функцией вида

• \ ко + ks + k^.s ² + k g S ³ + ...+ k_ms m

Н ( s ) =  --- ¹----2 2 mN , N >  m ,                                         (1)

• c 0 + C 1 s + c 2 s + C 3 s +^ + C n s

где s – комплексная переменная. Для удобства вводят комплексную переменную sn , нормиро- ванную по частоте среза юср: sn = V юср .

Порядок полинома знаменателя N характеризует порядок самого фильтра. Порядок числителя m зависит от порядка фильтра и его типа. Фильтры, у которых порядок полинома числителя нулевой, получили название полиномиальных фильтров. К таким фильтрам относятся фильтр нижних частот Бесселя, Баттерворта, Чебышева 1-го рода, фильтр с критическим затуханием и другие. Полиномиальные фильтры могут быть описаны передаточной функцией вида

Н ( s n ) =

23    N

¹ + ^c1 s n + c 2 s n + c 3 s n +- + c N s n

Амплитудно-частотная характеристика (АЧХ) фильтра находится по формуле G ( го ) = | Н ( j го )| при подстановке s = j ю или s_n = j го/го _ср . Как правило, передаточная функция фильтра нижних частот также нормируется по условиям:

• 1)    G ( 0 ) = 1 или заданному коэффициенту усиления G ( 0 ) = K ₀ при подстановке го = 0 ;

• 2)    G ( го _ср ) Jg ( 0 ) = 1Д/2 при подстановке го = го _ср или го _n = 1 . Частота среза ю_ср при этом должна быть заданной.

В данном случае условие нормирования п. 2 является также определением частоты среза.

Для практической реализации в виде активных фильтров выражение (2) целесообразно представить в виде

Н ( S n ) =

K 0

( 1 + a 1 S n + b S n )( 1 + a 2 S n + b 2 S 2 ) - ,

• т. е. в виде сомножителей второго порядка, где a 1 , a 2 , …, b 1 , b 2 , … – положительные коэффициенты.

Рассмотрим эти фильтры подробнее.

Фильтр нижних частот Баттерворта. Данный фильтр имеет максимально гладкую амплитудно-частотную характеристику на частотах полосы пропускания и снижающуюся почти до нуля на частотах подавления. Для фильтра первого порядка АЧХ снижается со скоростью –20 децибел на декаду (–6 децибел на октаву). Для фильтра Баттерворта N -порядка скорость снижения АЧХ определяется по формуле –20^∙ N децибел на декаду (–6^∙ N децибел на октаву). Фильтр Баттерворта нижних частот любого порядка – монотонно убывающая функция частоты. По сравнению с фильтрами Чебышева, эллиптическим фильтром, фильтр Баттерворта имеет более пологий спад АЧХ и потому должен иметь больший порядок, чтобы обеспечить нужные характеристики.

Фильтр Баттерворта определяется следующей зависимостью амплитудно-частотной характеристики:

или

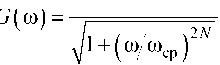
2 N

¹ + ( ^го/^го ср )

Gn (го) =

для нормированных частот ю n = го/ю_ср .

Отсюда определяются полюса фильтра Баттерворта:

j ( 2 k + N - 1 ) п

Sk = e   2 N где N – порядок фильтра; k – номер полюса, k = 1…N.

Полюса фильтра Баттерворта лежат на окружности комплексной плоскости, при этом рассматриваются только значения с отрицательной вещественной частью. Нормирование по пунктам 1 и 2 не требуется.

В табл. 1 представлены передаточные функции фильтров Баттерворта нижних частот для 1–4-го порядков.

Таблица 1

Порядок фильтра, N	Передаточная функция фильтра, приведенная к виду (2)	Передаточная функция фильтра, приведенная к виду (3)
1	H ( s n ) = s n ♦ 1	H ( s n ) = s n '+ 1
2	H ( sn ) = 2 rp 1 s n + 2 s. s n +1	H ( sn ) = 2 rp 1 s n + V2 s n +1
3	H ( s n ) = 3     2 V 7  s n + 2 s n + 2 s n + 1	H ( s n ) = (    1 V 2 ( sn + 1 ) ( sn + sn + 1 )
4	H ( sn ) = 4        3        ' V ’ s n + 2,61 s n + 3,41 s^ + 2,61 s n + 1	H ( s n ) =/ 2                  2             \ ( s„ + 0,765 sn + 1 ) ( s 2 + 1,85 sn + 1 )

Фильтр нижних частот Бесселя. Фильтр Бесселя обладает максимально гладкой групповой задержкой. В широком диапазоне частот сдвиг по фазе входного и выходного сигнала пропорционален частоте, что определяет линейность фазочастотной характеристики. АЧХ фильтра Бесселя нижних частот спадает не так круто, как у фильтра Баттерворта и Чебышева, что является недостатком. Однако преимущество фильтра Бесселя – оптимальная, с очень малым положительным выбросом переходная характеристика.

Коэффициенты фильтра Бесселя определяются по выражению

C ' k =

2 ( N - k + 1 ) k (2 N - k + 1)

C ' k — 1 , С о = 1, C 1 = 1,

где N – порядок фильтра; k – порядок степени s _n . Затем коэффициенты пересчитываются с учетом коэффициента нормирования:

C k = Y N c ' k .

Коэффициенты нормирования по частоте для фильтров Бесселя нижних частот 1–4-го порядков представлены в табл. 2.

Таблица 2

N	1	2	3	4
γ N	1,00	1,36	1,76	2,11

В табл. 3 представлены передаточные функции фильтров Бесселя нижних частот для 1–4-го порядков.

Таблица 3

Порядок фильтра, N	Передаточная функция фильтра, приведенная к виду (2)	Передаточная функция фильтра, приведенная к виду (3)
1	H ( s n ) = s n ‘+ 1	H ( s n ) = s n '+ 1
2	H ( s„ )=       2 V 7 0,618 s n 2 + 1,362 s n + 1	H ( s „ ) =       2 V 7 0,618 s 2 + 1,362 s n + 1
3	H ( sn )=         .         . V 7 0,3608 s 2 + 1,233 s 2 + 1,756 s n + 1	H ( s n ) =/                     2                \ ( 0,756 s n + 1 ) ( 0,477 s 2 + 0,9996 s n + 1 )
4	H ( s n ) = 1	H ( s n ) = 1
	" 0,19 s 4 + 0,9 s3 3 + 1,915 s 2 + 2,114 sn + 1	( 0,389 s n 2 + 0,774 s n + 1 ) ( 0,489 s n 2 + 1,34 s n + 1 )

Фильтр нижних частот Чебышева 1-го рода. Амплитудно-частотная характеристика фильтра Чебышева наиболее круто переходит от полосы пропускания к полосе непрозрачности. Фильтр Чебышева 1-го рода имеет неравномерности амплитудно-частотной характеристики в полосе пропускания, а фильтр Чебышева 2-го рода – в полосе подавления, по остальным показателям мало отличаясь от рассматриваемого фильтра Чебышева 1-го рода. Кроме того, фильтр нижних частот Чебышева 2-го рода, называемый также инверсным фильтром Чебышева нижних частот, имеет полином от комплексной переменной s в числителе. В переходных характеристиках обоих типов фильтров имеются существенные положительные выбросы, величина которых зависит как от порядка фильтра, так и от коэффициента пульсаций.

Амплитудно-частотная характеристика фильтра Чебышева 1-го рода строится по зависимостям:

G N ( to ) - H N ( j ®)| = /               = для нечетных порядков;

• V1 + (e TN (to nYn ))2

G N ( to ) - | H N ( j to)| - ,       + ⁶      = для четных порядков,

• V1 + (6TN (tonYN ))2

где N - порядок фильтра; e - коэффициент пульсаций; T N ( to _n у _n ) - полиномы Чебышева N -го порядка T _N ⁽ x ) при подстановке x -to _n у _n ; Y _N — коэффициент нормирования по частоте.

Коэффициенты нормирования для фильтров Чебышева 1-го рода 1–4-го порядков при ε = 1 представлены в табл. 4.

Таблица 4

N	1	2	3	4
γ N	1,00	1,168	1,00	1,041

Для других значений ε коэффициенты будут другие. Кроме коэффициента пульсаций ε используется связанный с ним коэффициент неравномерности АЧХ, измеряемый в децибелах. Например, неравномерности АЧХ для фильтра Чебышева 1-го рода 3 дБ соответствует коэффициент пульсаций ε=0,9976. В табл. 5 приведены передаточные функции фильтров Чебышева 1–4-го порядков.

Таблица 5

Порядок фильтра, N	Передаточная функция фильтра для ε= 1, приведенная к виду (2)	Передаточная функция фильтра для ε= 1, приведенная к виду (3)
1	H ( s n ) - s n '+ 1	H ( s n ) - s n '+ 1
2	H ( s« ) -     2 v ’ 1,93 s 2 + 1,065 sn + 1	H ( s« ) -     2 v ’ 1,93 s 2 + 1,065 sn + 1
3	H ( Sn ) - 3         2 V ’ 4 s n + 2,384 s n + 3,71 sn + 1	H ( s n )-/                      2              \ ( 3,356 s n + 1 ) ( 1,192 s n + 0,355 s n + 1 )
4	H ( S „ ) -      4        3        2 V 7 6,65 s 4 + 3,71 s n 3 + 7,17 s n + 2,38 s n + 1	H ( s n )-r      2                      2           \ ( 1,201 s n + 0,196 s n + 1 ) ( 5,54 s n + 2,2 s n + 1 )

Фильтр нижних частот с критическим затуханием. Отличительной чертой этого фильтра являются отрицательные действительные полюса, равные между собой. Если передаточную функцию (2) представить в виде

Н ( s n ) = 7------ ^ ^7,                                              (4)

( Sn -а1 )(Sn -а2 )( Sn -а3 ) — то а1 - а2 - а3 =^ = аi, и по условиям нормирования определится:

^а 1 ^-а 2 ^-а 3 = ^ = ^а i =---- ; K о ^-а 1 "  ^а 2 " ^а з -™" ^а / | .

V N 2 - 1

АЧХ фильтра с критическим затуханием спадает менее круто, чем у других рассмотренных фильтров, включая фильтр Бесселя, переходная характеристика не имеет выбросов.

В табл. 6 представлены передаточные функции фильтра с критическим затуханием 1–4-го порядков, приведенных к виду (4). Эти функции также можно привести к виду (2) и (3).

Таблица 6

Порядок фильтра, N	Передаточная функция фильтра, приведенная к виду (4)
1	H ( • ■    S n  1
2	2,41 H ( s„ ) = V n' ( s n + 1,554 ) ( s n + 1,554)
3	7,545 H ( S „ ) = n’ ( S n + 1,961 )( S n + 1,961 )( S n + 1,961 )
4	H ( s ) ____________________ 27,93 ___________________ 1 n) ( S n + 2,299 )( S n + 2,299 )( S n + 2,299 )( S n + 2,299 )

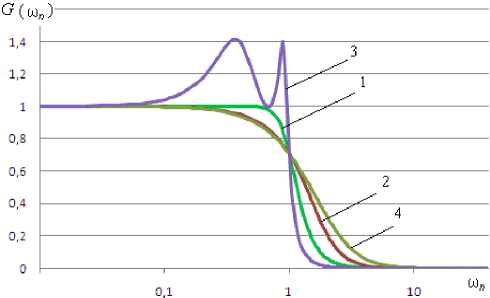
В целом, рассматривая передаточные функции фильтров нижних частот Баттерворта, Бесселя, Чебышева 1-го рода, фильтра с критическим затуханием, можно отметить, что для фильтров 1-го порядка всех этих типов передаточные функции одинаковы, для порядков N выше первого передаточные функции отличаются коэффициентами C _i (рис. 1).

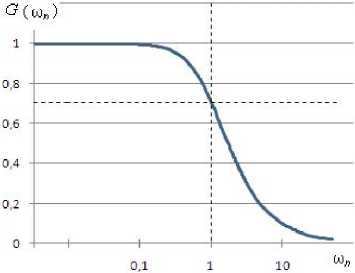
а)

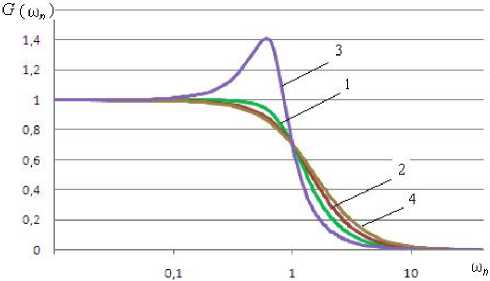
б)

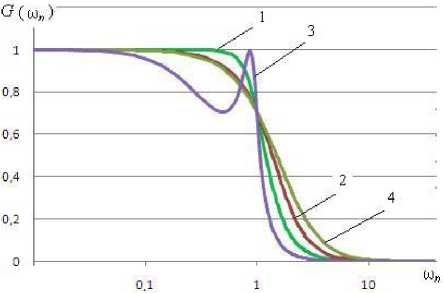
в)

г)

Рис. 1. АЧХ фильтров нижних частот Баттерворта, Бесселя, Чебышева 1-го рода при ε = 1, фильтра с критическим затуханием – кривые 1, 2, 3, 4; а – 1-го порядка, б – 2-го порядка, в – 3-го порядка, г – 4-го порядка

С увеличением порядка фильтра крутизна спада АЧХ возрастает. Но одновременно с этим усложняется реализация фильтра и увеличивается величина выброса переходной характеристики. Исключение – фильтр Бесселя, у которого, начиная с четвертого порядка выброс переходной характеристики уменьшается. У фильтра с критическим затуханием выброс отсутствует для любого порядка фильтра.

Для практического использования широкое распространение получили схемы активных фильтров нижних частот на операционных усилителях. Для любого порядка фильтров Баттерворта, Чебышева 1-го рода, фильтра с критическим затуханием можно составить выражения для непосредственного определения коэффициентов a i и b i в передаточной функции (3). При этом следует учитывать условия нормирования. Для фильтра Бесселя расчет коэффициентов a_i и b_i оказывается более сложной задачей.

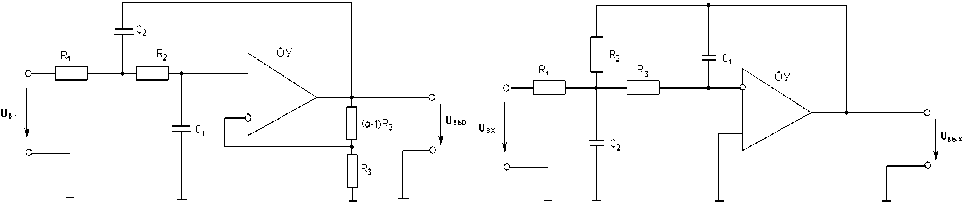
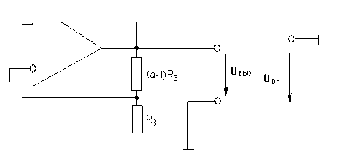
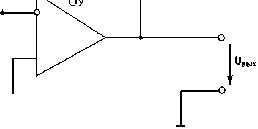
Рис. 2. Схема звена второго порядка с одной петлей Рис. 3. Схема звена второго порядка с многопетлевой положительной обратной связи                       отрицательной обратной связью

= с2 r2

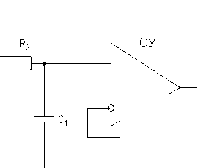
Кроме активных фильтров, в качестве фильтров нижних частот Баттерворта, Бесселя, Чебышева 1-го рода и фильтров с критическим затуханием могут быть использованы пассивные LC-фильтры. В литературе приводятся нормированные параметры четырехполюсников и методики выбора и расчета параметров. Пересчет элементов пассивных фильтров производится исходя из заданных сопротивлений нагрузки, частоты среза, других условий. Из фильтров нижних частот можно получить фильтры других типов, непосредственно заменяя одни элементы на другие, определяемые расчетом. При разработке активных фильтров важным ограничивающим фактором является верхняя граница частот пропускания активного элемента. Недостатки пассивных LC-фильтров: проблема получения высокой стабильности и добротности фильтра, главным образом из-за наличия катушек индуктивности; на низких частотах среза требуются большие номиналы элементов (при частотах среза порядка 1 кГц требуются индуктивности 0,01–0,1 Гн при нагрузке 1 кОм), что увеличивает габариты пассивных LC-фильтров, делает их неэкономичными; трудность создания сосредоточенных элементов на высоких частотах. При работе на высоких и сверхвысоких частотах могут быть применены электрические цепи с распределенными параметрами. Кроме того, могут применяться RLC-фильтры и фильтры других принципов действия: электромеханические, магнитострикционные, пьезокварцевые и пьезокерамические, акустоэлек-тронные, волноводные, параметрические и другие.

Современное развитие микропроцессорной и цифровой техники предоставляет широкие возможности реализации фильтров как программным способом, так и на основе цифровых интегральных микросхем. Следует учитывать квантование по времени и по уровню, которые присутствуют в цифровых устройствах, а также способы представления сигнала на входе и выходе.

Выводы. Рассмотренные полиномиальные линейные фильтры нижних частот обладают разными, порой взаимоисключающими характеристиками. Главное, что их объединяет – удобство реализации в виде каскадного соединения активных фильтров в ограниченном диапазоне частот, в виде каскадного соединения реактивных четырехполюсников по имеющимся в литературе методикам, и другими способами. Фильтры нижних частот могут служить прототипом при разработке других типов фильтров.