Физически обоснованная дискретизация времени в математических моделях генераторов регулярных и хаотических колебаний

Автоколебательные системы, осциллирующие в дискретном времени (ДВ-автогенераторы), интересны по крайней мере по двум причинам. Во-первых, они могут быть моделями реальных физических систем. Дискретное время здесь появляется в результате применения конечно-разностных алгоритмов к аналоговым моделям осцилляторов. В этом случае модели с дискретным временем должны с требуемой точностью воспроизводить характеристики аналоговых систем.

Во-вторых, нелинейные ДВ-автогенераторы могут рассматриваться как самостоятельные объекты динамики в дискретном времени. Зачастую они формируются по аналоговым прототипам, но точность воспроизведения свойств прототипов здесь не является главным требованием. Скорее речь идет об их качественном сходстве. При этом нелинейные ДВ-осцилляторы могут демонстрировать динамические эффекты, не наблюдаемые в непрерывном времени.

Традиционно для целей нелинейно динамики временная дискретизация аналоговых моделей проводится методом Эйлера. Первые исследования в этом направлении, по-видимому, выполнены в Б.Н. Чириковым [1] на основе комбинаций явного и неявного методов Эйлера. Аналогичным образом получено отображение Богданова [2; 3] и ряд других [4; 5]. Можно также использовать методы Рунге – Кутта высших порядков. Однако такой подход не дает замкнутых алгоритмов генерации ДВ-сигналов, т. к. предполагает применение внешних функций, задающих численные методы. Реализация этих функций средствами цифровой схемотехники сложна и, как правило, требует дополнительной дискретизации [6].

Более плодотворной, на наш взгляд, является физически обоснованная временная дискретизация с использованием представлений о колебательных процессах в системе [7].

В настоящей статье представлен метод дискретизации времени в математических моделях автоколебательных систем, основанный на сохранении временного отклика линейного резонатора системы. Изложение проведено на примерах генераторов Дмитриева – Кислова [8] и ван дер Поля.

1. Генератор Дмитриева – Кислова в дискретном времени

Систему дифференциальных уравнений движения аналогового прототипа – генератора Дмитриева – Кислова можно записать как d2 x + dt2

to o dx

Q dt

+ to o x — to o z ,

dz

+ to_r z — цto x exp( - x ), dt ^cc

где ® о и Q - собственная частота и добротность резонансного контура автогенератора; ro c - частота среза низкочастотного фильтра в цепи обратной связи; ц - параметр глубины обратной связи.

Предполагая в дальнейшем дискретизацию времени с интервалом А и введя в рассмотрение безразмерное время т = t / А, систему уравнений (1) запишем в виде d-X + -nv dx + 4n2Q- x = 4 n2Q- z,(2)

dt2       d т        00

dz + -nQcz = -nQc цx exp( - x-).(3)

Здесь частоты Q o , Q c и полоса резонатора v = Q o / Q измеряются в единицах частоты дискретизации ® d = -п / А .

Основным условием при проведении дискретизации времени в системе (2)–(3) считаем условие сохранения импульсного отклика линейного резонатора (2) на внешнее воздействие z(t). В теории синтеза линейных цифровых фильтров такой подход носит название метода импульсной инвариантности [9]. Для осциллятора (2) он дает разност- ное уравнение xn -25cos(-nQo)xn-1 +§2xn-- = = -nQo5 sin (-nQo) zn—i,

где параметр диссипации дискретного резонатора равен

5 = exp (-nv).

Следует отметить, что, согласно правой части уравнения (4), текущее значение осцилляций xn зависит от воздействия zn-i в предыдущий момент дискретного времени. Эта особенность примененной процедуры дискретизации позволяет сформировать рекурсивную систему без введения в аналоговый прототип дополнительных запаздываний.

Аналогично дискретизация времени по методу импульсной инвариантности преобразует дифференциальное уравнении (3) в разностное уравнение zn -Xzn-1 = -nQcцxn exp(-x- ),

где X = exp ( - - nQ c ) - параметр дискретного фильтра.

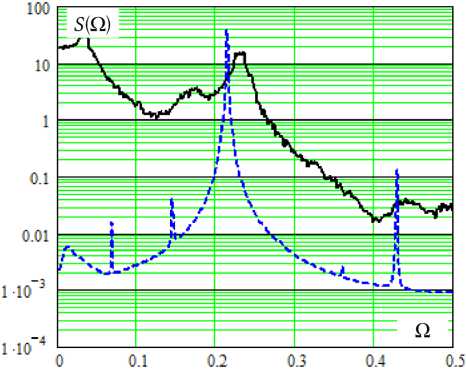
Таким образом, система разностных уравнений (4)–(5) определяет алгоритм генерации сигнала дискретным во времени генератором Дмитриева – Кислова. Режимы генерации определяются значениями совокупности четырех параметров Qo, Q, Qc, ц и варьируются от квазигармониче-ских до хаотических. На рис. 1 в качестве иллю- страции представлены периодограммные оценки спектров мощности S(Q) автоколебаний в генераторе со значениями Qo = 0.-1, Q = 30, Qc = 0.05 (X = 0.73). При этом параметр глубины обратной связи в первом случае равен ц = -.5 (пунктирная линия на графике), а во втором - ц = 6.75 (сплошная линия). Форма спектров указывает на то, что первый режим – это регулярные квазигармониче-ские автоколебания, второй – хаотические. Регулярные автоколебания совершаются в окрестности одной из двух неподвижных точек ±X:

± X = ±

- In

(1 - -5 cos (2nQ0 ) + 5- )(1 -X?

------------------------------------------------

4 n-Q0Q c ц5 sin (-nQ0)

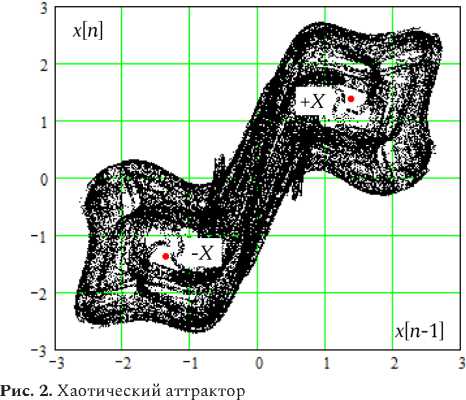
Хаотический аттрактор на плоскости ( x n - 1 , x n )

показан на рис. 2. Он формируется переходами между окрестностями указанных неподвижных точек.

Проведя перенормировку переменной z / ц ^ z , систему уравнений движения ДВ-генератора Дми-

триева – Кислова (4)–(5) можно записать в более компактной форме:

3. Генератор ван дер Поля

в дискретном времени

x n - 2 5 cos ( 2 KQ o ) x n - 1 + 5 2 x n - 2 = у z n - 1 ,            (6)

zn -X zn-1 = 2nQ cxn exp( - xn ), где через у = 2nQo^5sin (2nQ0) обозначен эквивалентный параметр глубины обратной связи.

Уравнение движения генератора ван дер Поля – автоколебательной системы томсоновского типа с кубической нелинейностью – запишем в виде (с безразмерным временем):

2. ДВ-генератор с инерционным возбуждением

Введем в кольцо генератора (6) дополнительный поворот фазы на угол п , тогда параметр у поменяет знак ( у ^ -у ), а дискретная динамическая система

d2x      dxdx

—- + 2nv   + 4n2Q0x = 2nvp (1 - x2 ) ,(7)

d т2       d т

x n ^{- 2 5 cos} ( ^{2 nQ} 0 ) x n - 1 + ⁵ 2 x n - 2 = ^-у z n - 1 , z n -X z_n - 1 = 2 nQ c x n exp( - X n )

где р – параметр превышения порога генерации (порог p = 1).

Принцип сохранения импульсного отклика подобно переходу (2) ^ (4) позволяет перейти от уравнения (7) в непрерывном времени к разност-

ному уравнению

x n ^{- 2 5 cos} ( ^{2 nQ} 0 ) x n - 1 ⁺⁵ 2 x n - 2 =

будет относиться к классу генераторов с инерционным возбуждением [10].

С учетом того, что 5 = exp ( -kQ q / Q ) и X = exp ( - 2 nQ c ) , режимы генерации в ДВ-системе (7) определяются значениями совокупности четырех параметров Q o , Q , Q c и у .

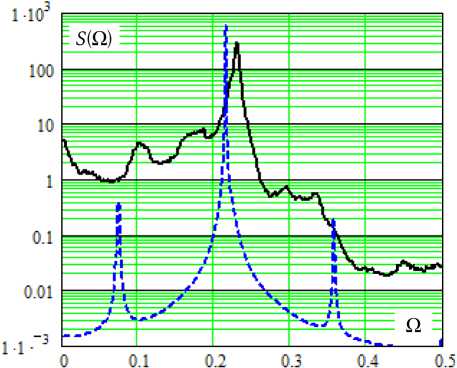
На рис. 3 в качестве иллюстрации представлены периодограммные оценки спектров мощности S ( Q ) автоколебаний в генераторе со значениями Q 0 = 0.21, Q = 30, Q c = 0.05 ( X = 0.73). При этом параметр глубины обратной связи в одном случае равен у = 1.25 (пунктирная линия на графике), а в другом — у = 9.69 (сплошная линия). Форма спектров указывает на то, что первый режим – это регулярные квазигармонические автоколебания, второй – хаотические.

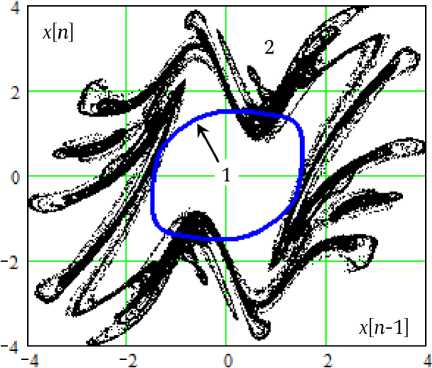
Фазовые плоскости x, x автоколебаний n-1 n показаны на рис. 4, где кривая 1 соответствует предельному циклу регулярных автоколебаний, множество 2 – хаотическому аттрактору.

= 2nv5p sinc (2nQ0) (1

x n - 1 ) y n - 1 ,

где sinc ( 2 nQ 0 ) = sin ( 2 nQ 0 ) /2 nQ 0 - кардинальный синус.

Дискретная переменная y_n – это отсчеты производной y ( т ) = dx / d т . Для их вычисления воспользуемся формулой

sinc (2nQ0) Уп = cos (2nQ0 )xn - xn-1.

Эта формула дифференцирования точна для гармонических колебаний и с учетом квазигармоничности автоколебаний в генераторе Ван дер Поля может быть принята в качестве приближенной. Тогда уравнение (8) принимает вид

x n ^{- 2 5 cos} ( ^{2 nQ} 0 ) x n - 1 ⁺⁵ 2 x n - 2 =

= 2 ^nv5 p ( 1 ^{- х}П - 1 ) ( cos ( ^{2 nQ} 0 ) x n - 1 ^- x n - 2 ) .

Разностное уравнение движения (9) определяет алгоритм генерации дискретного сигнала – ДВ-

генератор Ван дер Поля. При умеренных превышениях порога генерации ( p < 10) он воспроиз-

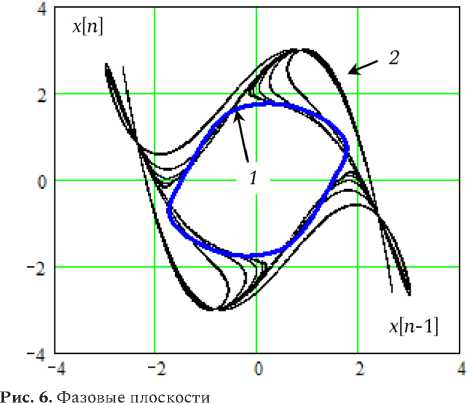
водит в дискретном времени основные свойства аналогового прототипа [8]. На рис. 5 (пунктирной линией) и рис. 6 (линией 1) представлены оценка спектра мощности и предельный цикл генератора (9) с параметрами Q o = 0.2, Q = 30 и p = 5. Эти характеристики типичны для режима регулярных квазигармонических автоколебаний. Но есть и особенность ДВ-автоколебаний, состоящая в подмене частот гармоник. На рис. 3 выделяются подмененные третья ( g3 ) и пятая ( g5 ) гармоники.

Создавая группу автоколебательных систем типа (9), можно определять их уравнением движения xn - 25 cos (2nQ0 ) xn-1 + 52xn-2 =

= 2 KVS p ( 1 - x n - 1 ) ( ^{K x}n - 1 - x n - 2 ) ,

где cos ( 2 nQ o ) 1. Отметим, что при значениях к ® 1 в ДВ-генераторе (10) достаточно легко реализуется режим хаотических автоколебаний (хаотический осциллятор ван дер Поля). Например, на рис. 3 сплошной линией показана оценка спектра мощности генератора (10) при к = 1 (остальные параметры сохраняют свои предыдущие значения). Хаотический аттрактор автоколебаний на рис. 4 представлен множеством 2.

Заключение

Использование физических представлений о процессах, протекающих в динамических системах, позволяет проводить дискретизацию времени в аналоговых моделях систем без привлечения численных алгоритмов высокого порядка точности, снижающих вычислительную эффективность и скорость обработки и формирования дискретных (цифровых) сигналов. Для систем с резонансными элементами дискретизацию времени целесообразно проводить на основе принципа сохранения импульсного отклика в аналоговых и дискретных резонаторах. Кроме того, скорость квазигармони-ческих осцилляций предполагается вычислять с помощью формул дифференцирования гармонических функций. Такой подход позволяет сформулировать рекурсивные алгоритмы генерации в дискретном времени регулярных и хаотических колебаний. Регулярные режимы генерации предлагается использовать для нелинейной фильтрации, например для синхронного детектирования дискретных сигналов с амплитудной и частотной модуляцией. Дискретные хаотические колебания позволяют, в частности, осуществлять маскировку полезной информации [11].

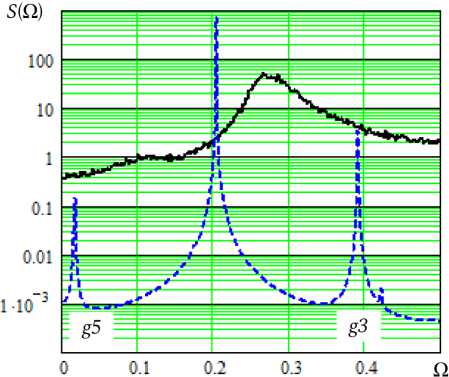
Рис. 5. Спектры мощности