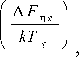Физический смысл параметров уравнения Бартенева для зависимости температуры стеклования от скорости охлаждения

С.Ш. Сангадиев, Б.Д. Сандитов, В.Б. Шагдаров и др. Физический смысл параметров уравнения Бартенева для зависимости температуры стеклования от скорости охлаждения

Известно, что характер изменения физических свойств в области стеклования одинаков для всех аморфных веществ независимо от их природы. Например, зависимость температуры стеклования T g стеклующихся систем от скорости охлаждения расплава q =d T /d t описывается одним и тем же эмпирическим соотношением, которое называют уравнением Бартенева [1],

— = C 1 - C 2 In q

^{T g}                   .                                       (1)

Отношение параметров данного уравнения оказалось универсальным для всех стеклующихся веществ (табл.) [2]

C

—^L ~ const ~ 0.03

^{C 2}                                                (2)

Данное сообщение посвящено интерпретации этого факта в рамках релаксационной теории [1-3] с привлечением модели возбужденного состояния [4], согласно которой жидкость переходит в стекло, когда средняя энергия тепловых колебаний решетки 3kT, отнесенной к атому, становится равной или меньше энтальпии предельной упругой деформации межатомной связи AHе: 3kT

^e re const re 2.5 + 3.5 kTg

,

что равносильно утверждению о том, что доля флуктуационного объема f=AVJV, образованного за счет критических смещений кинетических единиц из равновесных положений (А Ve=N_e-Au_e), при T= Tg достигает минимального постоянного значения f=fg [4]

re const re 0.02 + 0.03

.

Здесь N_e - число возбужденных кинетических единиц, Аи_е - элементарный флуктуационный объем, необходимый для реализации критического смещения (возбуждения) частицы.

Таблица.

Параметры уравнения Бартенева (1) и доля флуктуационного объема fg при температуре стеклования (использованы данные [2])

№1: SiO2 – 55.3, Na2O – 3.8, K2O – 9.2, PbO – 30, Al2O3 – 1.7; №2: SiO2 – 38.1, Na2O – 1.3, K2O – 2.5, PbO – 52, Al2O3 – 3.4, B2O3 – 1.8, CaO – 0.4, MgO – 0.4; №3: SiO2 – 70.9, Na2O – 16.1, K2O – 0.6, CaO – 8.1, MgO – 2.9, другие оксиды – 1.4; №4: SiO2 – 56, Na2O – 10.1, CaO – 17, MgO – 4, B2O3 – 2, Al2O3 – 11; №5: SiO2 – 57.6, CaO – 7.4, MgO – 8, K2O – 2, Al2O3 – 25. Составы стекол даны в мас.%.

Флуктуационный объем А V_e практически совпадает с флуктуационным свободным объемом аморфных веществ: Vf = Nh-u_h (Nh - число дырок, uh - объем дырки) [4]. С этой точки зрения образование флуктуационной дырки обусловлено критическим смещением молекулы, соответствующим максимуму силы межмолекулярного (межатомного) притяжения, иначе, процессом возбуждения молекулы (атома). Приближенное условие стеклования (4) выполняется для неорганических стекол, аморфных органических полимеров и металлических стекол (аморфных сплавов) [4].

Соотношение (1) можно вывести из релаксационной теории стеклования [1-3] с привлечением уравнения вязкости, записанного при температуре стеклования [5]

n

g

= n 0 exp

где AF_ng - свободная энергия активации процесса вязкого течения при T_g. При этом параметр С₂ приобретает следующий физический смысл

C2

k

A F n g

.

Принимая во внимание данное равенство, уравнение Бартенева (1) можно представить в виде

^AFng kTg

Из сравнения (5) с уравнением Дулитла [5] при T=Tg n g =n0exp(l/ fg )

следует связь свободной энергии активации текучести AF_ng с долей флуктуационного объема fg

№  1

ng « ^{1 kTg    fg} .                                         (8)

В рамках модели возбужденного состояния можно вывести уравнение Дулитла. При этом f принимает смысл доли флуктуационного объема [6]. Из выражений (7) и (8) приходим к выводу о том, что доля флуктуационного объема fg, замороженная при температуре стеклования, как и следовало, ожидать, оказывается функцией скорости охлаждения стеклообразующего расплава

—-f1-in q f- V C -V .                                    (9)

Авторы [2] предложили ввести стандартную температуру стеклования Tg^c как температуру, соответствующую вязкости n_g=10¹² Па-с (10¹³ П), ибо подавляющее большинство стеклующихся жидкостей переходит в твердое стеклообразное состояние именно при этой вязкости [5]

n(T_g) = n_g ~ const ~ 10¹²Па - с

Стандартной температуре стеклования соответствует скорость охлаждения q=1.8 град/мин=0.03 град/с. Примерно такая скорость q«1-3 град/мин используется во многих странах в дилатометрии стекол и аморфных полимеров. Поэтому можно считать, что имеющиеся данные о Tg относятся к стандартной температуре стеклования: T_g= T_g^c.

Зависимость Tg=Tg(q), как правило, является слабой и q входит в уравнения (1) и (9) под логарифмом: при изменении скорости охлаждения q в 10 раз температура стеклования смещается лишь на ATg«0.03T_g^c, где T_g^c - стандартная температура стеклования, AT_g=(T_g^c - T_g). Тем не менее, при более строгом подходе необходимо указывать, к какой скорости охлаждения относится значение fg. Принимая во внимание приведенные выше соображения, можно утверждать, что существующие в настоящее время данные о fg (а также данные об отношении (3)) соответствуют стандартной скорости охлаждения q=0.03 град/с и стандартному значению fg=fg^c.

Подставив в равенство (9) данное значение q (lnq=-3.5), получим стандартное значение доли флуктуационного объема (табл.)

f C,           1^-1

f = I--+ 3.5 I « const « 0.02 т 0.03 ^g

V C -         V

, которое согласуется с критерием стеклования (4).

Таким образом, постоянство отношения эмпирических коэффициентов уравнения Бартенева (2) можно рассматривать как следствие критерия стеклования в модели возбужденного состояния (4) [4]. Кроме того, проведенный анализ показывает, что доля флуктуационного объема fg, замороженная при температуре стеклования, зависит (хотя и слабо) от скорости охлаждения стеклообразующего расплава. Имеющиеся данные о величине fg относятся к стандартной скорости охлаждения q=0.03 град/с [2], применяемой в дилатометрии стекол и полимеров.