Fizik jarayonlarda oddiy differensial tenglamlarni o’rni

KIRISH

Fanlararo integratsiya - bir o'quv intizomining qonunlarini, nazariyalarini, usullarini boshqasini o'rganishda qo'llashda namoyon bo'ladi. Ushbu darajada amalga oshirilgan tarkibni tizimlashtirish talabalar ongida dunyoning yaxlit rasmini shakllantirish kabi bilim natijasiga olib keladi, bu esa o'z navbatida umumiy ilmiy tushunchalar, toifalar, yondashuvlarda o'z ifodasini topadigan yangi darajadagi bilim turini paydo bo'lishiga olib keladi. Fanlararo integratsiya fanlararo integratsiyani sezilarli darajada boyitadi.

Ushbu ishda fizika va differensial tenglamalari fanlari orasidagi integratsiya qanchalik muhim ekanligini quyidagi misollar yordamida ko’rib chiqilgan. Fizik jarayonlarni oddiy differensial tenglamlar yordamida yechish ko’rib chiqilgan.

Quyidagi ishlarda ham fanlararo integratsiya katta ahamiyat qaratilgan.[1],[2],[7],[22] ishlarda matematika va informatika fanlari orasidagi fanlararo integratsiyaga katta e’tibor qaratilgan. [3],[4],[5],[6] ishlarda algebra va geometriya fanlari orasidai integratsiya misollar yordamida ko’rsatilgan. [8],[9],[10],[11],[12],[13],[14],[15],[16],[17],[18],[19], [20],[21] ishlarda matematika, mexanika va fizika fanlari orasida integratsiyalarni ko’rsatib o’tilgan.

Tadqiqot ob’ekti va qo‘llaniladigan metodlar

Tadqiqot ob’ekti sifatida fizik jarayonlarni oddiy differensial tenglamalar yordamida yechish. Tadqiqot metodlari: masalani yechishning aniq usullari, taqribiy-aniq usullari va sonli usullari.

Olingan natijalar va ularning tahlili

Oddiy differensial tenglamalar haqida teorima va xossalarida foydalanib fizik jarayonlarni yechishni keltiramiz.

Эркин моддий нуқтанинг тўғри чизиқли ҳаракати. Эркин моддий нуқта тўғри чизиқли ҳаракат қилиши учун унга таъсир этувчи кучларнинг тенг таъсир этувчиси ўзгармас йўналишга эга бўлиши ва бошланғич тезлик эса тенг таъсир этувчи куч йўналиши бўйича йўналиши ёки нолга тенг бўлиши керак. Ҳаракат х ўқи бўйича содир бўлса, нуқта тўғри чизиқли ҳаракатининг дифференциал тенгламасини Ньютоннинг иккинчи қонунига биноан

dv

m — = F(x, v, t) dt

ёки

mx = F(x, v, t)

кўринишларда ёзиш мумкин.

Бунда ^—^ = — тезланиш харакат конунидан вакт буйича олинган иккинчи ва Г тезликдан t вакт буйича Олинган биринчи тартибли ҳосилалар, m — ҳаракатланаётган нуқта массаси, F — тенг таъсир этувчи кучнинг алгебраик қиймати.

• а)    Моддий нуцтага мицдор ва йуналиш жиуатдан узгармас булган F куч таъсир цилсин. Нуктанинг бошланFич тезлиги F кучнинг таъсир чизигида ётсин. х укни F кучнинг таъсир чизиги буйлаб йуналтирамиз. У ҳолда (1) тенгламани қуйидагича ёзиш мумкин:

mx = F

бунда F — кучнинг алгебраик киймати. (2) да x = —| эканлигини ҳисобга олиб, ўзгарувчиларни ажратамиз ва интеграллашдан сўнг

dx = — dt,

m

x = — t + С, m

ни ҳосил қиламиз.

• (3)    да хам x = ^ эканлигини эътиборга олиб, узгарувчиларни ажратамиз:

dx = (—t + С1) dt,

буни интеграллашдан сўнг —

x=-t2 + Cit+C2      (4)

ни топамиз.

• (4)    ифода (2) дифференциал тенгламанинг умумий ечимидир.

Ҳаракатнинг бошланғич шартлари t = 0 да х = x 0 , v =v 0 кўринишда бўлсин. У ҳолда уларни (3) ва (4) ифода ларга қўйиб, интеграллаш доимийлари   С 1  ва   С 2 ларни аниқлаймиз:   С 1 =v 0 , С 2 =x 0 . Топилган

қийматларни (4)га қўйиб, нуқтанинг ҳаракат қонунини аниқлаймиз:

X = Xn + Vnt + ^— t² 0 0m

• (5)    дан нуқта ўзгармас куч таъсири остида текис ўзгарувчан ҳаракатда бўлишини тушуниш қийин эмас.

• б)    Моддий нуқтага фақат вақтга боғлиқ куч таъсир этсин . F куч фақат t вақтнинг функцияси сифатида берилган бўлсин. У ҳолда (1) тенгламани қуйидагича ёзиш мумкин:

mx = F (t)

ёки туFри чизикли харакатда x = — = v,x = — (—У = — булгани dt            dt dt     dt учун m^ = F(t)

v = v 0 бошланғич шартда интеграллаб,

• (7)    тенгламани t = t 0 да хусусий ечимни ҳосил қиламиз:

t

+ v o

v = — I F(t) dr m to

Бу ечимни қуйидагича қайта ёзиш мумкин:

mv — mv₀ = f F(t) dr ^t o

• (8)    дан кўринадики, нуқтанинг бирор чекли вақт оралиғидаги ҳаракат миқдорининг ўзгариши таъсир этувчи кучнинг шу вақт оралиғидаги импульсига тенг (ҳаракат миқдорининг ўзгариши ҳақидаги қонун). F(t) маълум функция бўлганлиги учун охирги интегрални ҳисоблаб, вақтнинг функциясидан иборат бирор

f (t = f Fir) dr

t0

функция билан алмаштирсак, натижада (9) ни mv — mv0 = f (t)  (10)

кўринишда ёзиш мумкин. (10) дан нуқтанинг тезлиги v ни аниқлаймиз:

1 v = v₀ + —f(t) m

Бу тенгдамада v = — булгани учун dx

dt=^v 0 +m^f(t)

ёки ўзгарувчиларни ажратсак,

1 dx = v0 +—    dt

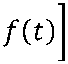
m бўлади.

Бошланғич t = t 0 пайтда х = х 0 дейлик. Бу бошланғич шартларда охирги тенгламани интеграллаймиз:

x = \ [-0 +—f (t)] dt + C to      m

ёки x = x0 + v0(t — t0) +I f(t)dt m to

Бу тенглама вақтга боғлиқ функция тарзида берилган ўзгарувчан куч таъсиридаги нуқтанинг тўғри чизиқли ҳаракат қонунини ифодалайди.

• в)    Моддий нуқтага фақат нуқтанинг ҳолатига боғлиқ куч таъсир

қилсин. У ҳолда (1) тенгламани dv m = F(x)

dt

ёки