Физико-химическая природа аномалий парамагнитных свойств монооксида никеля

Температурный ход зависимости хт должен соответствовать закону Кюри-Вейсса для антиферромагнетиков, который с учетом, что экспериментально установленное минимальное число магнетонов Бора на ион Ni²⁺ соответствует интервалу 3,4 <  Р < 3,5 [8] преобразуется к виду

^Р2 4ЛГг^

Z3KC ЗЛ(Т + 0) З^ТЧ#)’

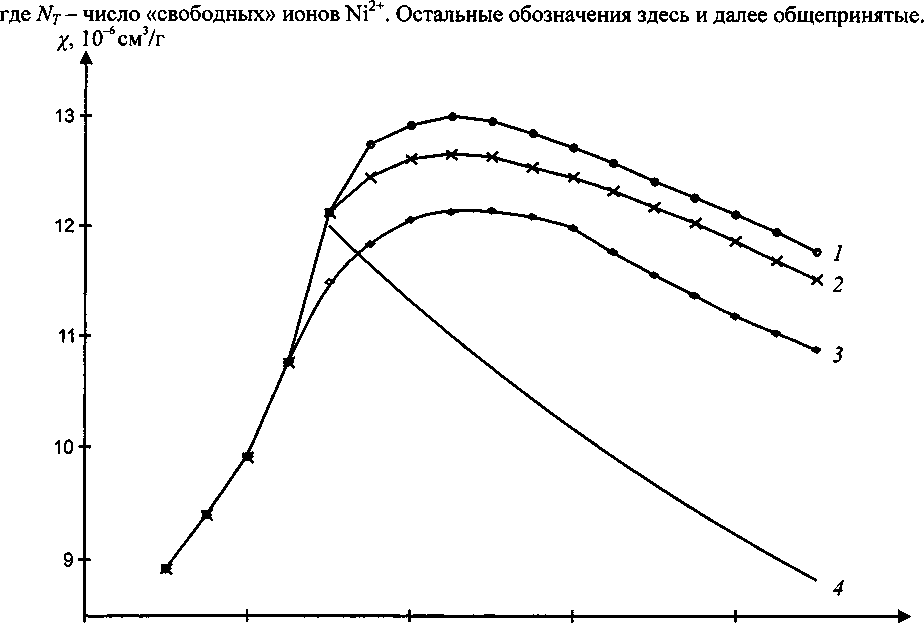
200            400            600            800            1000           Т, К

Рис. 1. Зависимость магнитной восприимчивости образцов NiO, полученных при температурах прокаливания:

1 -1300 °C, 2 -1100 °C; 3 -1000 °C; 4 - теоретическая зависимость

Величину и ход температурной зависимости дополнительного парамагнитного вклада от обменно-связанных ионов никеля можно определить исходя из модели Гейзенберга-Дирака-Ван Флека (ГДВФ) в соответствии со следующей последовательностью расчетов.

Модель ГДВФ базируется на гамильтониане

^пары =        - ^Б (4 + ^_z )Я ,                        (3)

который для случая 5] = S₂ = и/2 (n = 1, 2, 3,...) сводится к виду

Е = JS(S +1)-^(S")² - W_ZH,                    (4)

определяющему величину энергии в обменно-связанной паре. С учетом, что параметры S' = 0,1,2,...,25' и S'_z = -S', -5' + 1,...,5' имеют набор значений, для расчета суммы состояний (Z), среднего значения суммарной проекции спина ^S’_z ^ и намагниченности ^M_{z пар} ) использовали следующие равенства

S' 2S   -JSfS + p + ^SV'+O + Z/'s'S'z^

Z= X Z-p-------2—--------,(5)

S’Z=-S'S'=O

H'LS'zexpt-^A

>(6)

M^ = Nnap-2Mb-S^.(7)

Для условия 5[ = 52 = 1 равенство (7), с учетом (5) и (6), сводится к виду

Физика

sh

^Z,nap 4А_пар//_Б . ^

exp--+ l + 2ch I к! )

1 + ехр — + гъНЛ    (2J

—— + ехр —■ кТ )    [кТ

vWbH\ (2J}

>h ——— -exp —-

_{1 + 2ch} WL ₊ 2chM

кТ

кТ

из которого для случая слабых полей и высоких температур ц_ъН ]кТ <^\ получим выражение для температурной зависимости дополнительного парамагнитного вклада от концентрации обменно-связанных пар Ni²⁺-Ni²⁺.

*    _ В^пар^Б__1 + 5ехр(/ДГ)______ пар кТ 3 + 5ехр(2//А/) + ехр(-//АТ)’ где #пар - число пар. Поскольку полное число ионов никеля

^=^+2Упар,                        (10)

равенство (1), с учетом (2), (9) и (10), сводится к виду

"  ( J\ (6 Д .6 (2jV

4А_г//² 8А_пар                  ) Т ДкТ)

^/экс ЦТ + 0) кТ eV„ .  (2J>     ( /)V         ^{1 J}

ТД      VkT)  4 kT))

физический смысл которого очевиден. Первое слагаемое, это закон Кюри - Вейсса для идеальной антиферромагнитной кристаллической решетки NiO. Второе слагаемое это дополнительный парамагнитный вклад (А/) от обменно-связанных пар ионов Ni²⁺-Ni²⁺. Анализ его функциональной зависимости показывает, что величина отношения J/kT определяет не только величину А/, но и его знак. Если обменное взаимодействие в парах антиферромагнитное (/<0), то А/ < 0. В случае ферромагнитного взаимодействия (/ > 0) А/ > 0.

Таким образом, экспериментально наблюдаемый ход температурной зависимости /(7), а, следовательно, и отмеченные аномалии можно объяснить присутствием в кристаллической решетке пар Ni2+-Ni2+ из обменно-связанных ионов никеля с />0, сохраняющих ферромагнитную ориентации спинов до температуры Т = 563 К, при которой в [7] отмечен скачок теплоемко сти.

Для количественной оценки числа пар необходимы данные о численном значении параметров 0 и J, определяющих величину А/. Отметим, что оценка величины /из равенства полученного в теории усредненного поля [6]

ЗкТ

2zS(S + l)

существенно осложнена неопределенностью в выборе координационного числа (z) для пар. Согласно данному соотношению необходимо допускать изменение величины энергии обменного взаимодействия на порядок при переходе от пар из двух ионов (z = 1) к кластерам (z = 12).В [5, 6] отмечено, что значительные количественные изменения условий обменного взаимодействия возможны только при образовании группировок из более чем 1000 элементарных ячеек. В связи с этим численное значение параметров 0 и / оценивали в соответствии с принятой моделью ГДВФ на основании следующих допущений.

Анализ зависимости А/ (9) как функции двух переменных / и А_пар (рис.2) для изотермических условий показывает следующее. Величина А/ стремится к нулю в области отрицательных значений энергии (/<-0,2 эВ). При /<-0,1 эВ величина А/-8-10”⁸ см³/г сравнима с величиной погрешности при измерении. Это позволяет с учетом соотношения / = 0,1 эВ~к0 оценить величину постоянной 6 = 1160 К (800 см^-1) в законе Кюри-Вейсса (2) и согласно равенства (1) определить величину А/ и его температурную зависимость (рис. 3).

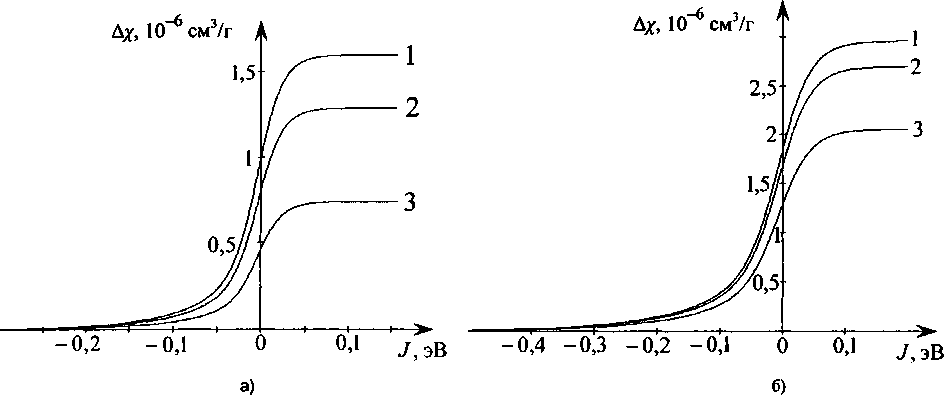
Рис. 2. Зависимость величины дополнительного парамагнитного вклада от величины энергии обменного взаимодействия и числа пар Ni2t- Ni2* при постоянной температуре:

а) 600 К; б) 1100 К. Цифры у кривых число пар х1О201 /г:

а) 1 - 0,96; 2 - 0,78; 3 - 0,45; б) 1 - 3,27; 2 - 2,98; 3 - 2,27

В области J > 0 величина Д/ определяется как функция двух переменных (рис. 2) до значений энергии J < 0,2 эВ. При J > 0,2 эВ величина Д/ достигает предельного значения и является функцией одной переменной (W_nap). Отмеченные особенности в ходе зависимости Д/ при J > 0 позволяет провести оценку числа пар по двум вариантам.

Первый вариант принят с учетом следующих положений. Зависимость Д/ от числа пар при изменении энергии обменного взаимодействия в интервале 0,2 эВ <  J < оо определяется равенством

Д/ = «^пар,                              (13)

где a - коэффициент пропорциональности при соответствующей температуре измерения.

Из вида данной зависимости следует, что при наличии в кристаллической структуре N1O постоянного числа пар величина энергии обменного взаимодействия не влияет на величину Д/. Это позволяет оценить величину коэффициента а и число пар из равенства

AZ3Kc=limAZ,                             (14)

где Д/_Экс - величина дополнительного парамагнитного вклада определяемая при соответствующей температуре измерения (рис. 3), Д/ - теоретическая зависимость определяемая равенством (9). Результаты вычисления в системе Maple 8 а и 7V_nap согласно равенству (13) представлены в таблице.

Для второго варианта оценки числа пар было принято, что энергия обменного взаимодействия не зависит от температуры измерения и термической предыстории синтеза образцов, а по величине равна половине интервала 0< J <0,1 эВ, где A_Zявляется функцией двух переменных Л^арИ ^ • В этом случае принятое значение энергии обменного взаимодействия (./ = 0,05 эВ) хорошо согласуется с величиной J = 0,0537 эВ рассчитываемой по Гейзенберовской модели для металлического никеля с температурой Кюри (7^ = 623 К).

Анализ при сопоставлении результатов количественной оценки числа пар (см. таблицу) позволяет сделать следующий вывод.

Величина относительной концентрации обменно-связанных пар с J >0 не более 10~² и, следовательно, их нельзя считать точечными либо линейными дефектами, а следует рассматривать

Физика

как кластеры (Ni2+ -Ni2+)„, обособленные либо когерентно связанные с кристаллической решеткой №0 при их статистическом распределении по объему кристаллов. Зависимость числа пар образующих кластеры от температуры спекания позволяет считать, что их химическая природа связана с термической предысторией синтеза образцов.

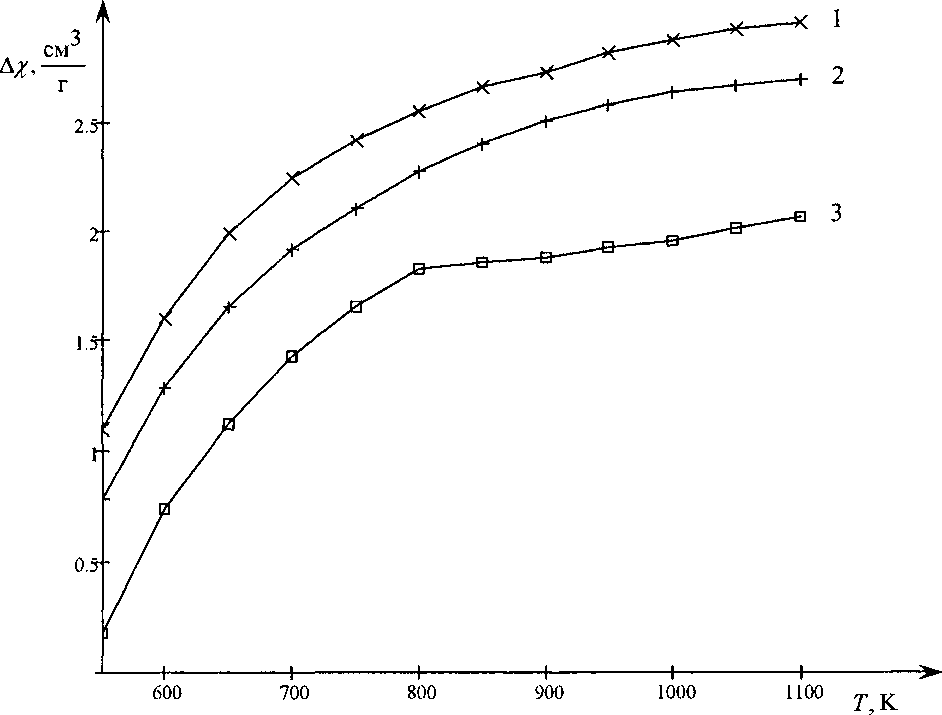
Рис. 3. Зависимость дополнительного парамагнитного вклада от температуры образцов, полученных при температуре спекания: 1 -1300 °C; 2 -1100 °C; 3 -1000 °C

Таблица

Расчетные значения числа обменно-связанных пар в структуре образцов NiO различной дисперсности

Температура измерения, К		600	700	800	900	1000	1100
a, IO'26см3		1,66	1,42	1,25	1,11	1,00	0,91
Число пар1 в структуре образцов, 1020 г"1, полученных при различ-ных температурах спекания	1000 °C	0,48 0,45	0,84 1,03	1,28 1,53	1,70 1,80	1,80 2,12	2,01 2,50
	1100 °C	0,72 0,79	1,20 1,39	1,76 1,91	2,16 2,41	2,50 2,87	2,96 3,27
	1300 °C	0,98 0,95	1,58 1,64	2,00 2,15	2,43 2,63	2,90 3,13	3,29 3,59

В заключение анализа физико-химической природы аномалий магнитных свойств NiO считаем необходимым отметить следующее. Предположение о наличии обменно-связанных пар (J > 0), сохраняющих ферромагнитную ориентацию спинов при температуре выше температуры Нееля противоречит утвердившимся теоретичеким положения [5] о невозможности их существования в идеальной кристаллической решетке NiO и при статистическом распределении в ней катионных вакансий. Однако вывод сделанный на основании теоретического анализа аномалий магнитных свойств NiO и количественных оценках числа пар находится в хорошем согласии с результатами авторов [9-12]. В данных работах предполагается существование в кристаллических решетках FeO, СоО и NiO связей Ме-Ме с термохимической энергией 127-146 кДж в расчете на один электрон, осуществляющий связь. Данная величина энергии близка к таковой в кристаллической решетке металла. При этом, как и в настоящей работе, наличие кластеров предполагается как естественное объяснение экспериментальных результатов термохимических и маг-нетохимических исследований. Вопрос о том, являются кластеры структуры временными элементами когерентно связанными с кристаллической решеткой NiO, либо представляют самостоятельные группировки из недоокисленных атомов никеля до настоящего времени остается дискуссионным.

Однако отмечено [10], что кластеры в составе NiO устойчивы и сохраняются даже при условии сильного разбавления магнитной структуры NiO.