Флуктуационный объем металлических стекол в области стеклования

Понижение температуры стеклообразующей жидкости до температуры стеклования T = T g приводит к тому, что объемная доля флуктуационного объема системы f уменьшается до некоторого минимального значения f = f g [1, 2]:

f = I - V - I   « const « 0.02 - 0.03,

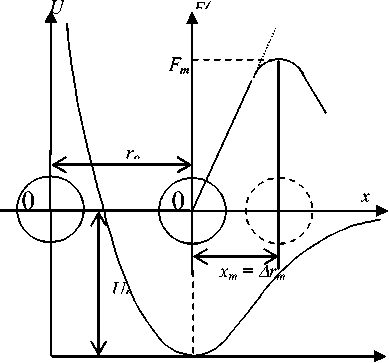
g к V ) T=Tg ниже которого (T

Модель возбужденного состояния предлагает возможный механизм, согласно которому возбуждение кинетической единицы сводится к ее критическому смещению Arm, соответствующему максимуму силы межатомного (межмолекулярного) притяжения (рис.) [1, 2]. Такие кинетические единицы (атомы, группы атомов) названы «возбужденными атомами». В силикатных стеклах в роли «возбужденного атома» выступает мостиковый атом кислорода во фрагменте кремнийкислородной сетки Si-O-Si, а в аморфных полимерах – небольшой участок основной цепи макромолекулы (группа атомов в повторяющемся звене). Данный подход – модель возбужденного состояния основан на обобщении концепции флуктуационного свободного объема [3-6].

Важным параметром модели является флуктуационный объем стеклующейся системы, обусловленный критическими смещениями возбужденных атомов из равновесных положений,

AVe = ( nr 2 Arm)Ne = NeAve, где Ne - число возбужденных кинетических единиц; nr2 - площадь сечения атома; Ave - элементарный флуктуационный объем, необходимый для процесса возбуждения атома:

Ave = nr 2 Arm .

Из термодинамической теории флуктуации плотности и модели возбужденного состояния следует связь объемной доли флуктуационного объема системы с относительной флуктуацией плотности в виде соотношения [7]:

Здесь v=V/N - объем, приходящийся на кинетическую единицу.

Рис. Схема механизма возбуждения атома (межатомной связи): ro - равновесное межатомное расстояние;

Arm - предельное смещение атома, соответствующее максимуму силы межатомного взаимодействия F_m [1, 2]

Если принять, что флуктуация плотности A A р / р )² =0, то флуктуационный объем аморфной среды будет равен нулю f=0. По этой и другим причинам V_e не совпадает со свободным объемом жидкостей и стекол, иначе, с объемом межатомного пространства [2, 6]. Задача настоящей работы - определить значения fg и других параметров модели для металлических стекол (аморфных сплавов) и сравнить полученные результаты с данными для аморфных полимеров и неорганических стекол.

Расчет параметров модели. Обсуждение результатов

Зависимость времени релаксации т (Т) и вязкости п (Т) в области стеклования от температуры описывается уравнением Вильямса-Ландела-Ферри (ВЛФ) [4]:

T - Tg ln aT = - C------g—’

^{T     1}T - Tg + C₂

где a_T=т (T)/t (T_g)=n (T)/n (Tg), C 1 и C₂ - эмпирические постоянные, которые в рамках модели возбужденного состояния получают следующую трактовку [2]:

C1 =¹/fg^;

C 2 = в f/fg, в = (df / dT)T - коэффициент теплового расширения флуктуационного объема при температуре fg стеклования.

Уравнение ВЛФ фактически эквивалентно известному уравнению Фогеля-Фулчера-Таммана

(ФФТ):

П = По expl T

B

-T

Константы этих формул образуют следующую связь [5]:

C1 =

B

т -т ’ go

С = Т - Т

C2 Tg T / о

Далее с учетом (1) и (2) есть возможность для расчета f_g и Pf по параметрам уравнения ФФТ:

fg =

Tg

To

B

P_f = 1/в.

Температуры плавления Tm, стеклования Tg и параметры уравнения Фогеля-Фульчера-Таммана для металлических стекол [8]

В таблице 1 приводятся значения параметров уравнения ФФТ для ряда металлических стекол, заимствованные из работы японских исследователей [8], а в таблице 2 – рассчитанные на их основе параметры модели возбужденного состояния.

Таблица 2

Параметры теории флуктуационного свободного объема для металлических стекол (использованы данные [8], см. табл. 1)

Примечание. c1 =B/(Tg-To), c2 = Tg-To.

Постоянные уравнений ВЛФ и параметры теории флуктуационного свободного объема для аморфных полимеров и неорганических стекол [2,4-6]

Примечание. U∞=R∙c1∙c2, fg=1/c1, βf =1/c1∙c2.

Следует обратить внимание на тот факт, что доля флуктуационного объема аморфных металлических сплавов, замороженная при температуре стеклования, нечувствительна к структуре и химическому составу этих систем (см. табл. 2)

f_g ≈ const ≈ 0.025 ÷0.027

и совпадает с данными для аморфных органических полимеров и неорганических стекол (табл. 3).

Имеющиеся данные fg и Tg, позволяют оценить энергию процесса возбуждения атома [1, 2]:

Δεe≅kTgln(1/fg)^.                                                      (³)

Величина Δεe ≅ 12-25 кДж/моль для аморфных сплавов (см. табл. 2) совпадает с такими же величинами для неорганических стекол (см. табл. 3). По-видимому, образование возбужденного атома в металлических стеклах представляет собой низкоэнергетический мелкомасштабный процесс, как и в других стеклообразных системах [2].

Для исследованных аморфных сплавов по формуле [9]

Ug = C1kTg                                                   (⁴)

вычисляли энергию активации вязкого течения при температуре стеклования Ug=U(Tg). Полученные значения Ug≈120-250 кДж/моль (см. табл. 2) по порядку величины близки к данным для неорганических стекол (см. табл. 3).

Значения коэффициента теплового расширения флуктуационного объема аморфных сплавов вбли- зи Tg (см. табл. 2)

βf =1/C1C2 ≈(2.0-2.8)⋅10-⁴K-¹

совпадают с данными для калиевоборатных стекол (см. табл. 3). Величина βf для многих стеклообразных систем совпадает со скачком коэффициента теплового расширения Δβ при температуре стеклования (см. табл. 3) [4, 5].

В области стеклования жидкостей и полимеров наряду с постоянством fg ≈ const установлены другие универсальные эмпирические и полуэмпирические правила и соотношения [5,10], например известное правило Симхи-Бойера:

ΔβT_g ≈ const ≈ 0.1 ^.

Полагая βf≈Δβ, мы проверили постоянство произведения βfTg для рассмотренных металлических стекол (см. табл. 2). За исключением ряда аморфных сплавов (Ni, Te, Ge) приближенно выполняется постоянство этого произведения: βfTg ≈ const ≈ 0,13-0,17.

В физике аморфных полимеров и стекол получил наибольшее распространение другой свободный объем, понятие о котором восходит к классическим работам Френкеля [14] и Эйринга [15] по дырочной теории жидкостей. Его часто называют флуктуационным [4, 5], иногда избыточным [12, 16] свободным объемом. Он обеспечивает молекулярную подвижность и играет доминирующую роль в молекулярнокинетических процессах, в частности в вязком течении жидкостей и аморфных веществ. Его объемная доля, замороженная при температуре стеклования, составляет около 2-4% [4, 5], что на порядок величины меньше доли геометрического структурно-обусловленного свободного объема.

Заключение

Если принять, что образование флуктуационной дырки происходит по механизму возбуждения кинетической единицы, то флуктуационный свободный объем совпадает с флуктуационным объемом в модели возбужденного состояния. Нетрудно заметить, что при такой интерпретации параметры теории флуктуационного свободного объема [2, 5] приобретают другой физический смысл. В частности, объем дырки vh приобретает смысл объема процесса возбуждения атома Δve, который определяется размером частицы (πr²) и масштабом предельной деформации межатомной связи (Δrm), а число дырок Nh – числом возбужденных атомов Ne. С этой точки зрения флуктуационный свободный объем vf=vhNh следует рассматривать как объем ΔVe=NeΔve, возникающий в результате критических смещений возбужденных атомов. Отсюда видно, что величина Vf=ΔVe не является свободным объемом как таковым в традиционном понимании последнего. Поэтому ее целесообразно назвать просто «флуктуационным объемом», а теорию свободного объема переименовать на «модель возбужденного состояния».