Фокальные распределения полей при наклонном падении излучения на геометрооптические фокусаторы. Фокусировка плоской волны в кольцо
Автор: Кобытев А.В., Курмышев Е.В., Сисакян И.Н.
Журнал: Компьютерная оптика @computer-optics
Рубрика: Численные методы компьютерной оптики
Статья в выпуске: 5, 1989 года.
Бесплатный доступ
Приводится численное исследование фокальных распределений полей, формируемых геометрооптическими элементами, фокусирующими наклонно падающую плоскую волну в кольцо с равномерным распределением интенсивности вдоль кольца. Определяется область применимости фазовой функции, реализующей указанные геометрооптические фокусаторы.
Короткий адрес: https://sciup.org/14058180
IDR: 14058180
Текст научной статьи Фокальные распределения полей при наклонном падении излучения на геометрооптические фокусаторы. Фокусировка плоской волны в кольцо
Плоские оптические элементы (ПОЗ), получающие все более широкое распространение в различных областях физического эксперимента и прогрессивных технологий [l], как правило, используются в отражательном режиме при наклонном падении излучения, что продиктовано очевидными технологическими требованиями построения оптических систем, а также необходимостью охлаждения таких элементов, предназначенных для фокусировки и коррекции излучения мощных технологических лазеров.
Наиболее развитыми как в математическом плане. Так и с точки зрения приложений являются математические модели синтеза ПОЗ, базирующиеся на приближении геометрической оптики [2-5]. Однако, как показывает анализ области применимости указанных алгоритмов и практики использования ПОЭ, в определенных областях параметров фокусаторов требуется более точное знание распределений интенсивности
-М- в фокальных областях с учетом волновой природы излучения. Задача формирования волновых полей с помощью оптических элементов для случая наклонного падения излучения имеет, как правило, более низкую симметрию в сравнении со случаем нормального падения волны. Этот факт значительно усложняет или делает невозможным аналитические расчеты (даже в зонах Френеля и Фраунгофера), обычно использующие сведение двукратного интеграла Кирхгофа к однократным и, возможно, последующее разложение в ряды по функциям Бесселя для осесимметричного случая или в ряды по другим функциям в зависимости от симметрии задачи [6-8], Поэтому в данной работе проведено численное исследование фокальных распределений полей, формируемых геометрооптическими элементами, фокусирующими наклонно падающую плоскую волну в кольцо с равномерным распределением интенсивности вдоль кольца.
Поставленная задача решалась с помощью соответствующей программы расчета двумерного интеграла Кирхгофа
u(P) = ^- fj ф(Е,П)| • ^r— dEdn, ...
2ni E r r где к=2п/Х - волновое число;
P(x,y,z) - точка наблюдения с координатами (x,y,z);
ф(Е,П) = A (g,п)е^*^,Г|’ - комплексное поле в плоскости z=+0 с вещественной амплитудой A(g,n) и вещественной фазой х(Е,П);
г2 = (х-g)2 + (у - п)2 + z2
и интегрирование ведется по плоской области Е (выходная плоскость ПОЭ), При выполнении условия кг » 1 интеграл (1) является решением первой краевой задачи уравнения Гельмгольца Ди + к2и = 0 с граничным условием Кирхгофа [7,8]. Отметим, что используемая нами программа расчета интеграла (1), созданная на базе метода Симпсона, позволяет рассчитывать волновые поля от ПОЭ произвольной (не только осесимметричной или прямоугольной) формы в широком диапазоне волновых параметров D = Xz/na2 >г 10-э, где а - характерный размер апертуры [9].
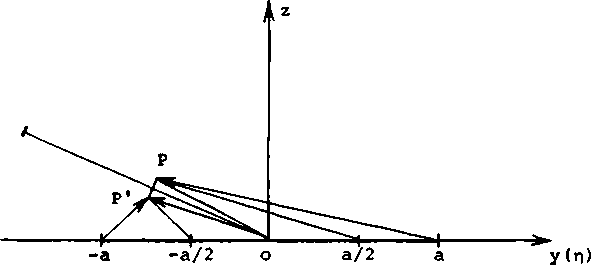
Итак, пусть ПОЭ располагается в плоскости ху (рис. 1). Плоская однородная волна падает на этот элемент под углом а к оси oz. Требуется сфокусировать такую волну в фокальное кольцо с равномерным распределением интенсивности вдоль кольца. Легко показать, что распределение фазы на выходной плоскости ПОЭ, решающее поставленную задачу в приближении геометрической оптики, дается выражением
х(Е,п) = - V(f + n-sin а) 2 + (р0 - Л;2 cos2 а + g2)2, (2)
где f - фокусное расстояние ОЭ (расстояние от центра 0 до фокальной плоскости);
Ро ~ радиус фокального кольца; а - угол падения.
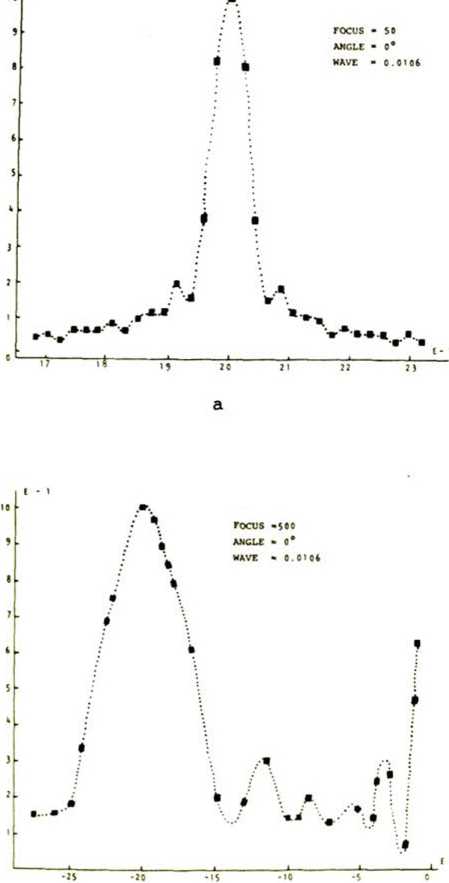
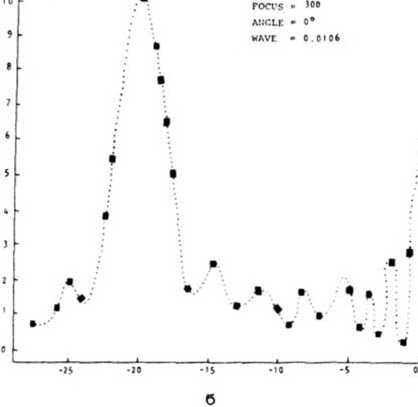
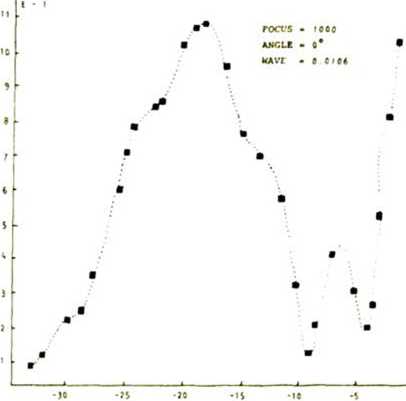
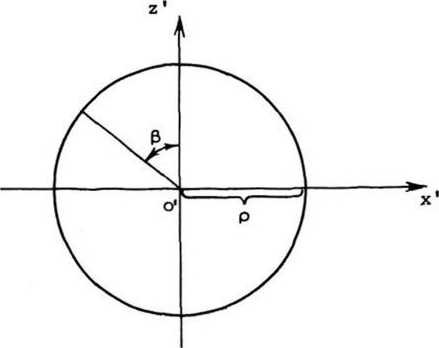
ПОЭ имеет форму эллипса с большой полуосью а = R/cos а и малой полуосью b=R,где R - радиус круглого фокусатора для случая нормального падения излучения -b С целью исследования описанного геометрооптического фокусатора мы провели численные расчеты волнового поля с помощью интеграла (1), используя в качестве выходной амплитудно-фазовой функции o(g,n) = А-е’’^^'^^, причем амплитуда была постоянной А = const, а фаза определялась выражением (2). Для всех расчетов длина волны X = 1.06 • 10"’ м, радиус круглого фокусатора R = 10-2 м, радиус фокаль- x(£j Рис. 1. Геометрия задачи ного кольца pQ = 2-Ю-3 м. Изменяемыми параметрами задачи были угол падения а = 0°; 30°; 45°; 75° и фокусное расстояние f = 3-10~а м; 5'10-2 м; 10“’ и; 3-10-1 м; 5•10—1 м; 1 м. Введем величину относительной интенсивности излучения l(f,p; а,В) = I(f,p; a,B)/l(f,p0; а,0°) в окрестности фокального кольца х,а + z'a = ра , расположенного в плоскости x'z* на расстоянии f от центра О оптического элемента. Здесь а - угол падения; В - полярный угол, отсчитываемый от оси o'z’ в плоскости x'z' (см. рисунки 1, 2). В силу симметрии задачи относительно плоскости yz(y'z') определяемой, кроме всего прочего, выбором расчетной сетки, интенсивность I(f,p; а,В) вычислялась при значениях полярного угла В = 0°; 45°; 90°, 135°; 180°, а а случае необходимости и при других значениях В. Отметим, что дополнительные контрольные расчеты для углов В = 225°; 270°; 315° полностью подтвердили указанную симметрию. ^"(n) Рис. 2. Фокальное кольцо Неравномерность распределения интенсивности вдоль фокального кольца описывается величиной I(f,po; а,В) при заданных значениях параметров f, ро, а и различных В. В таблице приведены результаты расчетов I для различных значений Распределение интенсивности поля вдоль фокального кольца В случае наклонного падения излучения на ПОЗ данные таблицы обнаруживают увеличение относительной интенсивности I при изменении полярного угла. Отмеченная регулярная неравномерность в распределении интенсивности вдоль фокального кольца при фиксированном а уменьшается с ростом фокусного расстояния f, а при заданном f она значительно возрастает с увеличением а. Причину наблюдаемого эффекта нетрудно понять из следующих соображений. Рассмотрим ход лучей от фокусаторов в соответствующие точки фокального кольца в плоскости х = 0 (см. рис. 1). В качестве наиболее контрастного примера геометрические построения приведены на рис. 3 для а = 75° и f - 30, 50 мм. Для других f и а рисунки и рассуждения аналогичны. Рис. 3. Положение фокального кольца относительно фокусатора в плоскости у=0 при а=75° и f=30, 50 мм - S7- Согласно геометрооптическому алгоритму каждая точка фокального кольца формируется соответствующим лучевым отрезком СЭ, так, например, реперная точка кольца Р с полярными координатами р0 = 2 мм и В = 0° формируется отрезком (0, а = R/cos а) оси оу, а отрезок (-а = -R/cos а, 0) отображается в точку фокального кольца Р’ с координатами р0 = 2 мм и В = 180°. Из рис. 3 и аналогичных ему рисунков для других f и а легко видеть, что при увеличении а из-за увеличения большой полуоси а = R/cos а апертуры фокусатора и в связи с приближением фокального кольца к ПОЭ происходит уширение формирующих лучков (на рис. 3 эти пучки ограничены лучами (-аР1) и (oP')z (аР) и (оР)), приводящее к нарушению условия параксиальности пучков (особенно для случаев малых f = 30, 50 мм), в рамках которого геометрооптическое решение задачи является корректным. Отмеченная непараксиальность приводит к замедлению сходимости результатов расчетов при измельчении сетки, то есть с увеличением а установление происходит на более мелких сетках. Другим следствием непараксиальности пучков является увеличение регулярной неравномерности распределения интенсивности вдоль геометрооптического кольца при росте а. Рассматривая участки лучевых отрезков фокусатора как источники вторичных сферических волн, амплитуда которых затухает по закону А -1-1 , легко оценить отношение интенсивностей, например, в точках фокального кольца Р и Р* по приближенной формуле 1(Р*)/КР) * [1(Р)/1(Р')]2, (3) где 1(Р) - расстояние от середины отрезка (о,а) до точки Р; 1(Р') -расстояние от середины отрезка (-а,о) до точки Р'. Оценки по формуле (3) для различных значений f и а не только качественны, но и по порядку величин верно отражают установленную в результате численных расчетов регулярную неравномерность распределения интенсивности вдоль кольца, объясняя тем самым ее происхождение и отличие результатов расчета по формуле (1) от геометрооптических расчетов фокусатора [2], предсказывающих равномерность интенсивности вдоль кольца. Практический интерес представляет ширина фокального кольца, то есть р -распределение интенсивности при заданных значениях параметров f, а, В» В данной работе относительные интенсивности I(f, р; а,В) = I(f,р; а,В)/I(f,РО; а,В = 0°) при различных фокусных расстояниях f = 30, 50, 100, 300, 500, 1000 мм и углах падения а = 0°, 30°, 45°, 75° вычислялись в фокальной плоскости x’z1 вдоль оси О ' Z ' . Расчет распределений интенсивности при а = 0° и f = 30, 50, 100, 300, 500, 1000 мм дает следующие результаты, которые представлены в виде характерных графиков на рис. 4. Отметим, что без потери существенных особенностей поведения кривых на графиках представлено значительно меньшее число расчетных точек, отмеченных квадратиками. Ввиду общей структурной схожести графиков для фокусных расстояний f = 30, 50, 100 мм эти распределения представлены одним графиком с f = 50 мм (рис. 4а); для всех указанных фокусных расстояний четко выделяется основной пик распределения в окрестности точки р ■ pQ. Ширина фокального кольца, определяемая полушириной главного пика распределения Кр) в окрестности точки Р = Ро , для случая f = 30 мм составляет ~4Х, для f = 50 мм - яг7А, для f = 100 мм-А13Л. Рис. ^ . Радиальное распределение интенсивности поля а окрестности геометрического кольца при нормальном падении излучения: a) f =• 50 мм; б) f = 30 0 мм; в) f = 500 мм; г) f = 1 00 0 мм Для указанных выше фокусных расстояний величины вторичных максимумов в окрестности основного максимума р = р0 не превышают 20$ от величины основного пика, имея тенденцию к росту с увеличением f. Расчеты для фокусных расстояний f = 300, 500, 1000 мм проводились не только в окрестности точки р = Оо, но и по всему диаметру фокального кольца. Ширина фокального кольца для f = 300 мм со-ставляет^Ц, для = 5 00 мм - х75А, для f = 10 00 мм - х 1 50А (см. рис. А б, в, г). Таким образом, с увеличением f наблюдается сильное дифракционное размытие гео-метрооптического кольца, которое сопровождается следующими эффектами: - происходит значительное изменение Формы главного пика (рис. ^г); - максимум главного лика смещается от точки р = р0 в сторону центра фокаль- - происходит рост максимума в центре фокального кольца с последующим разде лением этого пика на два относительно центральной точки х* = z' = 0 фокального коль ца . Исследование зависимости формы главного пика р - распределения интенсивности фокального кольца от различных углов падения а и фокусных расстояний f проводилось следующим образом. На основе формул (1) и (2) были рассчитаны распределения относительных интенсивностей I(f,p; а,В=0°) для фокусных расстояний f = 30, 50, 100 мм и углов падения излучения а = 0°, 30°, 45°, 75°. В случае f = 100 мм график р - распределения I (р) для всего диапазона углов падения а = 0°, 30°, 45°, 75° практически не меняется и имеет вид, аналогичный рис. 4а, причем полуширина главного пика составляет примерно 13Х. Для f = 30, 50 мм общая картина зависимости соответствующих р - распределений I(f,p; а,В=0°) от углов а похожа на случай с f = 100 мм - графики указанных р - распределений в окрестности точки р = ро остаются практически неизменными и имеют вид рис. 4а с полуширинами главных пиков 7Х и 4Х соответственно. Однако следует отметить, что с уменьшением f и увеличением а вследствие нарушения параксиальности формирующих пучков сходимость результатов расчетов при увеличении числа узлов расчетной сетки происходит на значительно более мелких сетках так, что для случая f = 30 мм и а = 75° при разумном времени счета на ЭВМ типа VAX р-распределение не установилось. С целью определения влияния граничных условий Кирхгофа [8] на полученные выше результаты для случая f = 50 мм и а = 0°, 30°, 45°, 75° были получены распределения интенсивности I(f,p; а,В) с учетом аподизации ПОЗ. Модуляция амплитуды отраженной волны с фазой (2) на выходной плоскости фокусатора описывалась выражением [10] A(g,n) = Ао ехр(1п тт1п(^- + ^t)N), (4) где а = R/cps а; b = R - большая и малая полуоси эллипса; Tmin ” минимальный уровень отражения падающей плоской волны с амплитудой Ао на границе апертуры; N - параметр "жесткости" аподизации. Как показали расчеты, учет аподизации при т = 10-3 и N = 50 приводит к min изменениям распределений относительной интенсивности не более чем на 1% от соответствующих распределений без учета аподизации. Таким образом, в данной задаче разрывные граничные условия Кирхгофа оказывают сравнительно небольшое влияние на результаты расчетов. Следует отметить, что использование аподизации ПОЗ в форме, отличной от (4), может привести к выравниванию распределения интенсивности вдоль фокального кольца. В заключение кратко суммируем результаты работы. 1. Наблюдается сравнительно быстрая сходимость результатов расчетов (до уровня Д1 = II(N) - I(N')I/I(N) < е = 10"3) при переходе от сетки N х (N/cos а) узлов к более мелкой сетке N' х (N*/cos а) . Сходимость зависит как от f , так и от а: для f > 100 мм, как правило, достаточно сетки с N = 256(512); для f $ 50 мн необходимы сетки с N > 512(700). 2. В случае нормального падения излучения в диапазоне f = 30-1000 мм наблюдается: - значительное дифракционное размытие основного пика р - распределения интенсивности в окрестности геометрооптического фокального кольца при f > 100 мм; - наличие и изменение пика р - распределения интенсивности в центре фо кального кольца при изменении f; - смещение максимума основного пика р - распределения к центру фокального кольца (при f = 1000 мм,Др = -4Х). 3. Для исследованных в работе геометрооптических фокусаторов, рассчитанных под различные углы падения излучения а, с увеличением а при данном f наблюдается рост регулярной неравномерности распределения интенсивности вдоль фокального кольца. Указанная неравномерность при фиксированном угле а убывает с ростом фокусного расстояния f. 4. В данной задаче разрывное граничное условие Кирхгофа оказывает незначительное влияние на результаты расчетов интеграла Кирхгофа.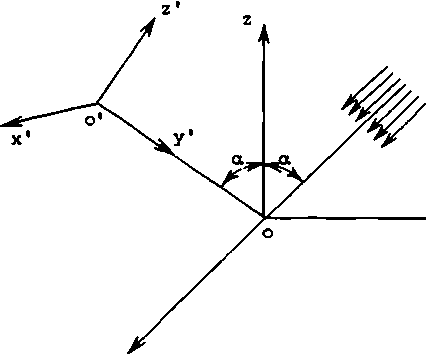
\f(M) о
а \
3 • 1 о-2
5-10~2
1 О-1
з-ю-1
5- Ю-1
1
1
1
I
1
1
1
0.999
0.999
0.999
1
0.999
1
0°
1
1.001
1
0.999
1
0.999
0.999
0.997
0.999
1
0.999
1
0.999
0.999
0.999
1
1
1
1
1
1
1
1
1
0.958
1.024
1.012
1.012
1 . 006
1 . 004
30°
1 . 046
1 .078
1.047
1 .038
1.017
1.013
1.146
1.141
1 .069
1 . 047
1 . 023
1 .022
1.203
1.179
1.095
1 .044
1 . 025
1 .026
1
1
1
1
1
1
1 . 064
1 .03
1 . 021
1.012
1.012
1 .006
45°
1 .242
1.129
1 . 06
1 . Об
1 .034
1 .023
1 .478
1 .257
1.121
1 . 065
1.043
1.038
1 .622
1.312
1.142
1 .057
1 .047
1 .045
1
1
1
1
1
1 .088
1 .053
0.999
1.001
1.017
75°
1.451
1 .245
1 .072
1 . 099
1 .073
2.432
1 .529
1.159
1 .098
1.136
3.576
1 .774
1.169
1 .093
1,16
f и а в точках фокального кольца, определяемых значениями полярного угла 0 = 0°; 45°; 90°; 135°; 180°.