Фокусировка лазерного излучения на трехмерную поверхность вращения

В задачах технологии лазерного поверхностного упрочнения и легирования материалов актуальной является фокусировка лазерного излучения в трехмерные поверхности.

В работах [1-4] сообщалось о создании фокусаторов лазерного излучения в плоские линии и плоские области.

В данной работе рассматривается задача фокусировки лазерного пучка на трехмерную поверхность общего вида, получены и проанализированы решения задачи фокусировки радиальносимметричного лазерного пучка на поверхность вращения.

• 2.    ПОСТАНОВКА ЗАДАЧИ

• 3.    РАСЧЕТ ЭЙКОНАЛА ФОКУСАТОРА

Пусть лазерное излучение с комплексной амплитудой W₀(u) = \/^(?)exp[ik^₀(u)]. где 1₀(и) - интенсивность освещающего пучка, Ф_обЪ — эйконал пучка, к = у- - длина волны, падает на фокусатор с апертурой С, расположенный в плоскости z = -f_Q, (рис. 1), который преобразует падающее излучение в поле W(iT) = = W₀(u)exp[ik^(u’)] = x/i^(5)exp [ik ^,6Г)] ,где ^(u) - эйконал фокусатора, tf'jttf) = *q(u) * V'(u) - эйконал непосредственно за фокусатором. Требуется найти эйконал фокусатора ^б?), обеспечивающий на поверхности S, описываемой уравнением z = f(x, у), заданное распределение освещенности Е(х, у).

Рис. 1. Геометрия задачи фокусировки

Поверхность фокусировки предполагаем непрозрачной и не содержащей областей геометрической тени. Будем называть пару точек с координатами (х, у, f(x, у)) G S и (u, v) G G "сопряженными”, если луч, соединяющий эти две точки, пересекает поверхность фокусировки только один раз и угол между этим лучом и нормалью к поверхности фокусировки не превышает^ (нормаль направлена к теневой стороне поверхности фокусировки). Поверхность фокусировки не содержит областей геометрической тени, если все точки поверхности имеют сопряженные в области фокусатора.

Расчет эйконала фокусатора будем проводить в геометрооптическом приближении.

Пусть

х = x(u,v) y = y(u,v).

Функции, описывающие лучевое соответствие между точками поверхности фокусировки и точками фокусатора.

Предполагая отображение (1) взаимно однозначным, закон сохранения светового потока запишем в виде

Е₀(и, у) =

-,   , , Эх Эу

Е(х,у) [— du Эу

Эх Эу, Эу Эи

Cos(a)

где Е₀(и, у) = I_Q(u, v)Cos(^), /3 - угол между нормалью к плоскости фокусатора и падающим в данную точку лучом, а а — угол между нормалью к поверхности фокусировки и осью z,

Cos(a) = У1₊( ^))2₊₍ЭГ(х,у)₎₂

Эх          Эу

Корректное задание EQ(u, у) и Е(х, у) требует выполнения условия нормировки:

/Е (7)d2u = JE(?)dS.(3)

GS

Из уравнения эйконала несложно получить уравнение наклонов:

grad [ ф ] (u)] = Х ~U             =■.(4)

x/(fQ + z(x))2 + (х - и )2

Из уравнения наклонов можно однозначно восстановить эйконал ф(и)_э если выполняется условие интегрируемости:

rot I                              1 = 0.(5)

V(f0 + Z(x))2 + (x - u)2

Эйконал фокусатора Ф(и) = Ф । (u) - Ф₀(и), определяемый из уравнений (2)—(5), является допустимым решением только в том случае, если соответствующее лучевое соответствие (1) связывает только сопряженные точки.

• 4.    РАСЧЕТ ЭЙКОНАЛА ФОКУСАТОРА РАДИАЛЬНО-СИММЕТРИЧНОГО ЛАЗЕРНОГО ПУЧКА НА ПОВЕРХНОСТЬ ВРАЩЕНИЯ

Рассмотрим случай радиальной симметрии комплексной амплитуды освещающего пучка WQ(p) = = Vl0(p) exp [ik Ф0(р)], р = Vu2 + V2, р < R, R — радиус фокусатора и функции распределения освещенности Е(г), г = vx2 + у2 на поверхности фокусировки S, полученной вращением кривой г = r(z) вокруг оси z. Функцию г = r(z) будем называть образующей поверхности S.

Вследствие радиальной симметрии задачи фокусировки, эйконал фокусатора является радиальной функцией и может быть определен из следующих уравнений:

dz(p) _ dp

Е„(р)р _________

E[r(z)] r(z)Vl + (^ )2 dz

*(p) = J -—==^==- dp - t₀(p) -⁰ V(f₀^{+ z}(p ))² + (r (z(p )] - p )²

Уравнения (6), (7) получены переходом к полярным координатам из закона сохранения светового потока (2) и уравнения наклонов (4). Условие интегрируемости (5) также является выполненным, что может быть легко про- верено непосредственным вычислением. Эйконал фокусатора, определяемый из уравнений (6), (7), будет являться решением задачи фокусировки, если лучевое соответствие г = r[z(p)] = 6(р) связывает только сопряженные точки. Как отмечено в п. 2, лучевое соответствие г = 9(р) связывает сопряженные точки в том случае, если угол меж ду направлением падающего луча и направлением нормали к теневой стороне поверхности меньше, чем™, то есть

(Т, П) > 0,                                                                                               (8)

где 1 = (L + z(p), 9(р) - р) - вектор луча; п = ( ^^У, , -1) - вектор нормали. ^и                                          dz

В частности, при фокусировке плоского пучка в сферический сегмент с образующей r(z) = VR2-^ - Rj)2,0< z< а,

R| - радиус сферы (рис. 2) и с постоянным распределением освещенности, условие (8) может быть приведено к виду:

21L

Rj * f

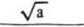
R2^! +0

р2 x/2R]R2 —ар2

Ра

R2

p e [0, R].

Уравнение (9) определяет взаимосвязь физических параметров, при которых возможна фокусировка в сферический сегмент.

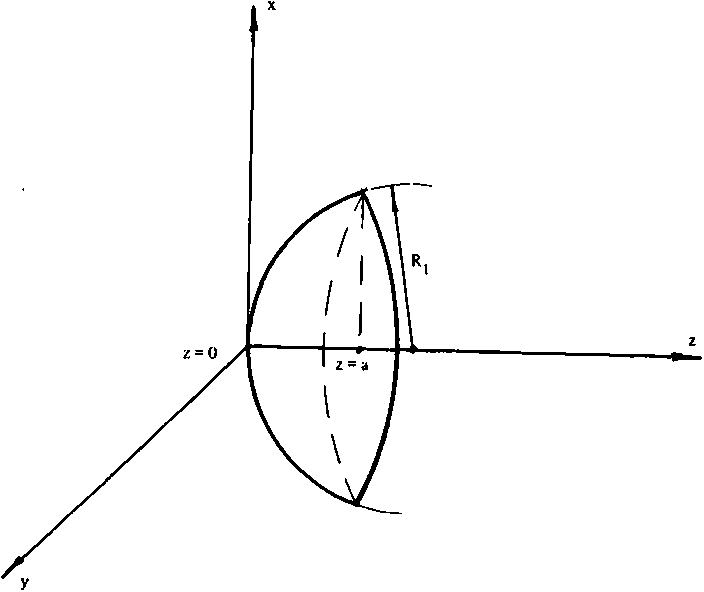
Рис. 2. Геометрия сферического сегмента фокусировки

• 5.    ИССЛЕДОВАНИЕ РЕЛЬЕФНО-ФАЗОВОЙ СТРУКТУРЫ ФОКУСАТОРОВ

Одной из важнейших характеристик фокусаторов, синтезируемых методами компьютерной оптики, является минимальный размер зоны микрорельефа 8.

В случае радиальной симметрии эйконала фокусатора размеры зон микрорельефа Д могут быть получены из следующего уравнения

|ф(р + Д)-ф(р)1 = Х.

d ф

Полагая ^(р + Д) - ф(р) = ^ А* Для определения размера минимальной зоны микрорельефа 6 имеем соот ношение

X

max у— pe[O,R]ldP

При фокусировке плоского пучка на поверхность конуса с образующей r(z) = tg(a)z, 0 < z < а (рис. 3) и распреде пением освещенности Е(г) = сг11, размер минимальной зоны микрорельефа 8П (п - показатель степени в распределении освещенности) может быть получен из (6), (7), (11) в виде:

8„ = Xlmax 0G(O,R]

tg(a)a(^)ⁿ⁺² -р

<„-ф"2

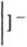
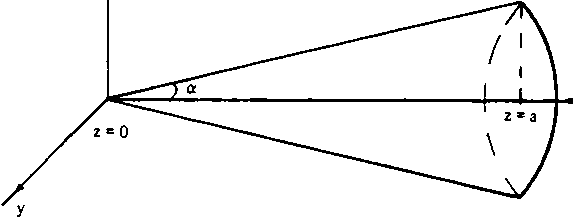
Рис. 3. Геометрия конуса фокусировки

Используя (12), можно легко получить общую оценку минимальной зоны микрорельефа, справедливую при любом распределении освещенности на конусе фокусировки.

6 <

X(f0+a)

max |р — atg(a)| pe[0,R]

Интересно отметить, что оценка (13) совпадает с оценкой минимальной зоны микрорельефа фокусатора в кольцо с радиусом atg(a) и фокусным расстоянием fQ + а.

При а -*0 оценка (13) переходит в оценку минимальной зоны линзы, а при а -» 0 и а-* ’ так, что atg(a) = const, оценка (13) переходит в оценку минимальной зоны для фокусатора в круг с радиусом atg(a).

В случае фокусировки плоского пучка в сферический сегмент (см. рис. 2) из (6), (7), (11) может быть получена следующая оценка:

5 <

X(f₀ + а) ______________ max |р - Vr, - (R. - а)² pe[0.R]         ^{1     1}

Уравнения (12), (13), (14) могут служить для определения физических параметров при фокусировке в конус и сферический сегмент, согласованных с технологическими возможностями фотопостроителей, используемых при синтезе фокусаторов [5].

В таблице для фокусаторов на поверхность конуса при наиболее типичных физических параметрах приведены размеры минимальных зон микрорельефа 60, соответствующие постоянному распределению освещенности и оценки минимальной зоны микрорельефа 8, справедливые для произвольного распределения освещенности на поверхности конуса.

Данные таблицы свидетельствуют о технологичности рассмотренных фокусаторов и возможности их изготовления при использовании существующих фотопостроителей, размер растрового пятна которых лежит в диапазо-

Параметры X (мкм) 6g (ММ) 6 (мм) fQ = 800 ММ 10,6 1,697 1,242 R = 12 мм 5 0,8 0,586 а = 12 мм а =5 2,94 0,47 0,344 6 fg = 150 ММ 1,06 0,108 0,048 R = 5 мм а = 6 мм 0,63 0,064 0,028 а= 1 6 не от 1 мкм до 50 мкм. Требования к технологии изготовления таких фокусаторов не превышают требований к ранее изготовленным фокусаторам в кривые и плоские области [2—4].

• 6.    РЕЗУЛЬТАТЫ ЧИСЛЕННОГО ИССЛЕДОВАНИЯ

3.00 12 .*00 ?

Для исследования эффективности предложенных фокусаторов был проведен численный расчет поля в фокальной области фокусаторов плоского пучка (WQ(p) = 1, р < R) в конус и сферический сегмент. Для расчета поля в фокальной области использовалось параксиальное приближение интеграла Кирхгофа и численные методы, рассмотренные в [6,7]. На рис. 4 приведено нормированное распределение освещенности вдоль образующей конуса (см. рис. 3) от фокусатора в конус с постоянным распределением освещенности при X = 10,6 мкм, fQ = 800 мм, а =5, а = 12 мм,

—1— 9.00

Рис. 4. Нормированное распределение освещенности вдоль образующей от фокусатора в конус с постоянным распределением освещенности

R = 12 мм, а на рис. 5 — нормированное распределение освещенности от фокусатора в конус с линейным распределением освещенности при X = 5 мкм, fQ = 800 мм, а =5, а = 12 мм, R = 12 мм. Минимальные размеры зон микрорельефа для указанных фокусаторов составляют 1,697 мм и 0,5 мм. На рис. 6 приведено нормированное распределение освещенности вдоль образующей (см. рис. 2) от фокусатора в сферический сегмент с постоянным распределением освещенности при X = 10,6 мкм, fQ = 300 мм, R] = 8 мм, а = 6 мм. Оценка размера минимальной зоны микрорельефа составляет 0,42 мм.

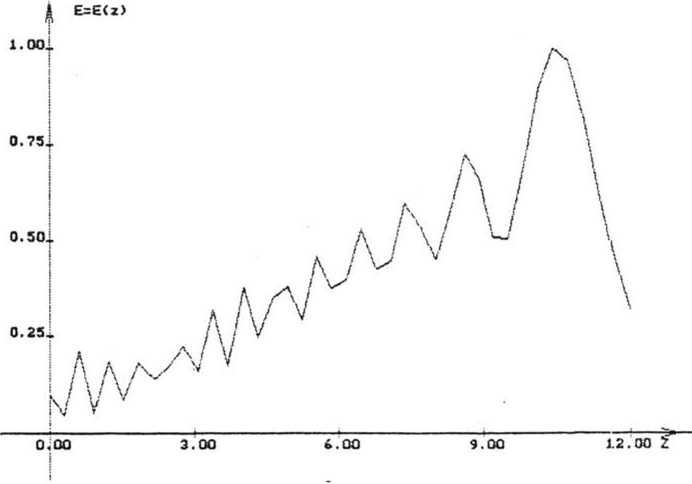
Рис. 5. Нормированное распределение освещенности вдоль образующей от фокусатора в конус с линейным распределением освещенности

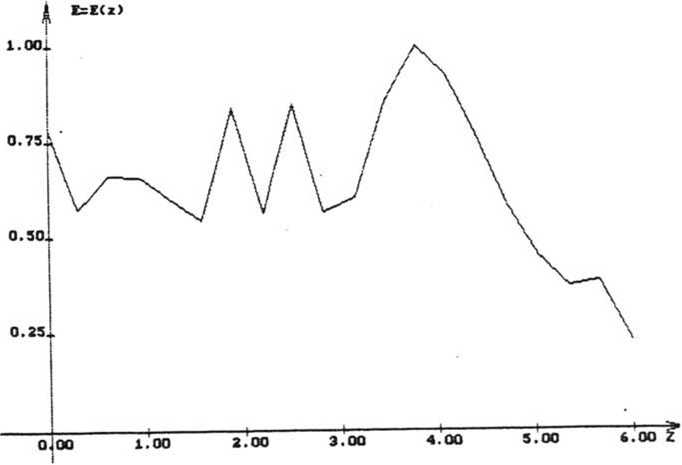
Рис. 6. Нормированное распределение освещенности вдоль образующей от фокусатора в сферический сегмент с постоянным распределением освещенности

Полученная в результате численного исследования оценка энергетической эффективности рассмотренных фокусаторов, то есть для энергии освещающего пучка, попавшая на поверхность фокусировки, составляет не менее 86%. Результаты численного расчета полностью подтверждают работоспособность приведенного подхода к расчету фокусаторов на трехмерную поверхность вращения. Полученные оценки размеров минимальных зон микрорельефа обеспечивают возможность изготовления предложенных фокусаторов на фотопостроителях типа РНОТОМА-TION-P1700 (минимальный растр 12,5 мкм).