Фокусировка лазерного излучения в прямолинейно-скругленные контура

Фокусаторы, синтезируемые методами компьютерной оптики, открывают возможность формирования сложных контурных конфигураций в фокальной плоскости. Решение прикладных задач маркировки алфавитно-цифровыми символами, создания реперных знаков, генерации фотошаблонов делает актуальной задачу фокусировки лазерного излучения в сложную фокальную область, составленную парциальными отрезками прямых и дугами окружностей. В частности, фокусировка в контур, представляющий буквенно-цифровую информацию, может осуществляться "составными" фокусаторами в набор отрезков и полуокружностей. Развитый в настоящее время комплекс аналитических и алгоритмических средств [1-7] позволяет решать задачу синтеза фокусатора в прямоли-иейно-скругленные контура в полном объеме, включая следующие этапы:

• 1.    Разложение составного фокального контура на парциальные отрезки прямых и дуги окружностей.

• 2.    Выбор разбиения составного фокусатора на соответствующие сегменты.

• 3.    Решение парциальных обратных задач фокусировки из сегментов фокусатора в парциальные отрезки прямых и дуги окружностей и сшивка парциальных решений для получения фазовой функции фокусатора.

• 4.    Выполнение вычислительного эксперимента путем численного решения прямой задачи.

• 5.    Формирование фотошаблона и реализация соответствующего фокусатора.

• 2.    ПОСТАНОВКА ЗАДАЧИ ФОКУСИРОВКИ РАДИАЛЬНО-СИММЕТРИЧНОГО ЛАЗЕРНОГО ПУЧКА В СИСТЕМУ ОТРЕЗКОВ И ДУГ ПОЛУОКРУЖНОСТЕЙ

• 3.    СВЕДЕНИЯ К ЭТАЛОННЫМ ЗАДАЧАМ ФОКУСИРОВКИ В СИСТЕМУ ОТРЕЗКОВ И ПОЛУОКРУЖНОСТЕЙ

В работе [1] предлагалось маркировочную метку приблизить набором точек и использовать фокусатор, состоящий из сегментов, представляющих сектора крута, каждый из которых фокусирует излучение в соответствующую точку маркировочной метки. Недостатком указанного подхода является неравномерность распределения интенсивности на контуре маркировочной метки.

В работе [2] рассмотрен фокусатор в набор отрезков с постоянной интенсивностью. Предполагалось, что апертура фокусатора должна состоять из секторов круга, каждый из секторов обеспечивал фокусировку в соответствующий отрезок фокальной области. Недостатком предложенного фокусатора является сложная зависимость вида функции эйконала на сегменте от взаимной геометрии положения сегмента фокусатора и отрезка фокусировки, а также ограниченные возможности передачи скругленных частей алфавитно-цифровых символов при маркировке.

В данной статье предлагается новый метод синтеза фокусатора в систему произвольно расположенных отрезков и полуокружностей с постоянной интенсивностью, основанный на единообразном разбиении фокусатора на концентрические кольца и учитывающий симметрию освещающего пучка даже при неосесимметричной функции эйконала.

Пусть радиальносимметричный лазерный пучок с комплексной амплитудой W₀(u) = A_o(u)exp(ik0_o(u)] = = W₀(p), р = vu²*" v² , где A_Qfu) - амплитуда освещающего пучка, Ф₀(и) — эйконал пучка, k =-^, X - длина волны, падает на фокусатор с круглой апертурой G радиуса R, расположенный в плоскости J = (u, v) при z = О (рис. 1), который преобразует падающее излучение в поле W(u) = W_Q(u)exp[ik^(u)],где ф(и) - эйконал фокусатора. Задача состоит в отыскании эйконала фокусатора i/i(u) , обеспечивающего при z = f в плоскости х = (х, у) формирование светового поля с постоянным распределением интенсивности 1(х) на контуре, состоящем из N парциальных отрезков и L полуокружностей. Положение каждого элемента в фокальной области будем характеризовать набором параметров Qj = [dj,(Xj, ур, Ojj ,j = 1,М, где М = N + L, dj - длина отрезка или полуокружности, (Xj, yj) - смещение центра отрезка или центра полуокружности относительно начала координат, Oj — угол, составленный отрезком или хордой полуокружности с положительным направлением оси х.

Особенностью приведенной задачи фокусировки является вид области фокусировки, представляющей набор из элементов двух видов — отрезков и полуокружностей. Для решения поставленной задачи предлагается использовать составной фокусатор, основанный на разбиении круглой апертуры фокусатора на сегменты в виде концентрических колец Gj радиусов Rj_p Rj, отражающих симметрию освещающего пучка. Представление фокусатора как набора колец Gj (см. рис. 1), каждое из которых фокусирует излучение в произвольно расположенный элемент Dj - отрезок или полуокружность, позволяет предложить универсальный метод расчета эйконала фокусатора ^(u, v). Эйконал i^j(u, v) в пределах кольцевого сегмента Gj при фокусировке в элемент фокальной области, описываемый набором параметров Qj = {dj, (Xj, yj), a J , может быть получен из эйконала ^j(u.v) кольцевого сегмента, рассчитанного на фокусировку в элемент с "эталонной геометрией”, то есть в элемент с параметрами Qj = {dj, (0,0), 0}. Действительно, выполняя поворот системы координат u, v на угол ttj и добавляя линейные по переменным и и v функции, описывающие смещение элемента фокусировки относительно начала координат, можно получить, что в параксиальном приближении

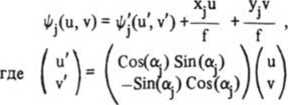
Таким образом, кольцевое разбиение делает задачу расчета эйконала кольцевого сегмента инвариантной к геометрии положения соответствующего элемента фокусировки, и решение исходной задачи фокусировки основывает- ся на решении элементарных задач фокусировки пучка с кольцевым сечением в отрезок и полуокружность с ’’эталонными геометриями”. Поскольку сегменты фокусатора не пересекаются, то эйконал составного фокусатора в набор из отрезков и полуокружностей имеет вид:

М          2p-(R. ,+RJ

^(u, v) = S [Mu, v)rect (      1 ---7- )],

где rect(x) =

О, иначе.

Потребуем равномерного распределения всего светового потока освещающего пучка по парциальным отрезкам и

полуокружностям, тогда радиусы Rp j = 0,М могут быть определены из следующего рекуррентного уравнения к.

J

S I_Q(p)2tfpdp = pdp

Rj-1

где Ro = 0,

10(р) - интенсивность освещающего пучка.

4. РЕШЕНИЕ ЗАДАЧИ ФОКУСИРОВКИ В ОТРЕЗОК

Рассмотрим задачу фокусировки радиально-симметричного лазерного пучка кольцевого сечения с комплексной амплитудой

WQ(p) = A0(p)exp[ik^0(p)]rect[

2р - (R, + R2)

в отрезок с постоянной интенсивностью

1(х) =

I, |х|<4,у = 0

0, иначе,

где R1 и R2 - внутренний и внешний радиусы кольца. В работе [8] рассмотрен метод расчета фокусатора в отрезок, основанный на дифракционной аппроксимации оператора распространения света, полученной из асимптотического разложения интеграла Кирхгофа в параксиальном приближении. Согласно [8] эйконал фокусатора кольцевого пучка в отрезок в параксиальном приближении имеет вид:

+ / K(i)d{-^0(u,v), - Ro

где функция к(|) отображает ось и плоскости фокусатора на отрезок в фокальной плоскости. Согласно [8] к (£) определяется из решения следующего дифференциального уравнения

ак«) _ . d{

Г * A0(j,v)dv]2

с граничными условиями

k(-R2) = -^, k(R2) =^

Согласно [8], распределение интенсивности в фокальной плоскости фокусатора (4), (5) обладает значительно большей равномерностью во внутренних точках отрезка фокусировки по сравнению с соответствующим распределением от геометрооптического фокусатора.

Интересно отметить, что формулы (4), (5) имеют вид, аналогичный геометрооптическим [4], но с предыска-женным законом соответствия x(i). Предыскажение учитывает дифракционное размытие поперечной ширины отрезка из-за дифракции на слоях [4] различной длины в плоскости фокусатора.

5. РЕШЕНИЕ ЗАДАЧИ ФОКУСИРОВКИ В ПОЛУОКРУЖНОСТЬ

Рассмотрим задачу фокусировки лазерного пучка с комплексной амплитудой (3) в полуокружность радиуса Ro с постоянным распределением интенсивности у > 0, х2 + у2 = R2

11(х,У)= *

О, иначе.

В случае фокусировки в полуокружность эйконал может быть определен из условия фокусировки в точку полуокружности (х, у) лучей, проведенных от прямой v = и [4], так что для случая параксиального приближения эйко

нал имеет вид                          _____

. и² + у² . RqxXi^ + v- ф(и, v) =---— + Sign(-v) ----------

- *0(и,у).

где

Sign(v) =

l,v>0

0,v = 0

-l,v<0

6. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО РАСЧЕТА

Расчет поля в фокальной области от фокусатора в контур, составленный из отрезков и полуокружностей проводился с использованием параксиального приближения интеграла Кирхгофа и численных методов, рассмотренных в [8,9].

Для характеристики качества фокального изображения используются следующие величины: значение энерге-Л l(x)d2x тической эффективности Е и среднеквадратичного отклонения 6. Величина Е=В---_ —— характеризует долю

Л10(и)<12и

энергии падающего пучка, попавшую в окрестность D фокального контура S с дифракционной шириной Д- =   —-.

КГКН

Величина 6 = J- (^ / (!(х) - I ]2dS]^ характеризует близость распределения интенсивности на контуре фокуси ровки к постоянной величине, где |S| - длина контура Si = — /T(x)dS - среднее значение интенсивности на кон-ISI $

туре фокусировки. Численный расчет поля проводился для фокусаторов в буквы "А" и ”Р”.

На рис. 2 приведено трехмерное распределение интенсивности от фокусатора Гауссова пучка с интенсивностью

10(р) = ехр(-—), р < R в букву "А", составленную из отрезков с длинами 11,2 мм, 11,2 мм, 5 мм при следующих а2

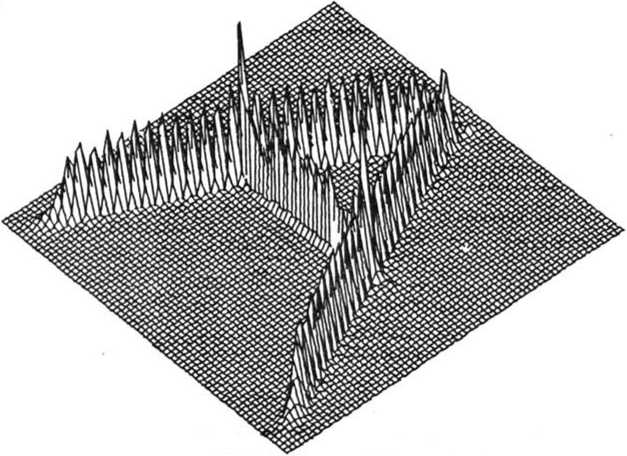
Рис. 2. Трехмерное распределение интенсивности от фокусатора в букву "А"

физических параметрах: Х = 5 мкм, Г=250мм, о = 4,94 мм, R = 7,5 мм. Энергетическая эффективность фокусировки в букву ’’А” составила 85,2%, а среднеквадратичное отклонение — 21,4%. На рис. 3 приведено трехмерное распределение интенсивности от фокусатора Гауссова пучка в букву "Р”, составленную из отрезка длиной 10 мм

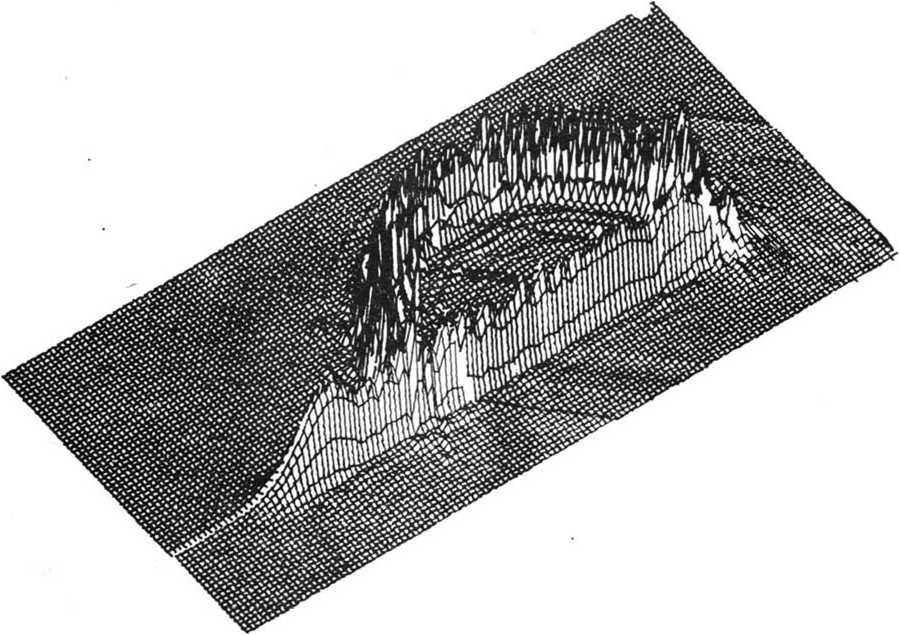
Рис. 3. Трехмерное распределение интенсивности от фокусатора в букву ”Р”

и полуокружности радиусом 3,5 мм для X = 10,6 мкм, f = 250 мм, о = 4,94 мм, R = 73 мм. Энергетическая эффективность фокусировки в букву "Р" составила 863%, а среднеквадратичное отклонение - 20,1%. Приведенные результаты численных расчетов подтверждают работоспособность разработанного подхода к расчету фокусаторов в сложные фокальные контура.