Форма массового пика линейной ионной ловушки с цилиндрическими электродами при квадрупольном резонансном возбуждении колебаний ионов

Для создания идеального квадрупольнoго поля вида U ( x,y ) = U 0 ( x ² - y ² ) / r ₀² требуется изготовление электродов с гиперболическим профилем с прецизионной погрешностью. На практике вместо гиперболических электродов часто используются аппроксимирующие их цилиндрические электроды. Очень важным преимуществом является то, что в отличие от гиперболических электродов изготовление круглых стержней технологически проще, и они могут быть собраны в квадрупольный блок (конденсатор) с микронной погрешностью без привлечения сверхточных и дорогостоящих технологий.

Однако в результате замены идеальных гиперболических электродов на приближенные цилиндрические электроды создаваемое электрическое поле будет отличаться от идеального квадрупольного поля. А именно, кроме основной квадрупольной компоненты поля

U ⁽²⁾( ^x, y ) = A 2 ( x ^{2 -} y ² )/ ^r 02 =A 2 ( p ²/ ^r 02 ) cos ( 2 ф )

(где введены обозначения p = p ( x , y ) = ^ x ² + y ² , Ф = ф ( x,y ) = arctan ( y / x ) ), в системе будет неизбежно присутствовать сложная совокупность пространственных мультипольных гармоник вида

U ( x,y ) = E U ⁽ 4 k+ ^{2 )}( ^x, y ) = k

=u0 Те a4 k+2 (p / ro )4 k+2 cos ((4 k+2) ф )1, L k _ где A4k+2 — неизвестные коэффициенты мульти-польного разложения. Коэффициенты Ak однозначно определяются безразмерным геометрическим параметром y = r / r0 (где r — радиус электродов, r0 — радиус вписанной окружности между вершинами этих электродов). В зависимости от выбранного значения параметра γ будут меняться соотношения между паразитными гармониками A4k+2 (k > 1). Тем самым практически важным моментом является оптимизация геометрии квадруполя, т. е. выбор такого значения γ , при котором поведение реального квадруполя с цилиндрическими стержнями будет минимальным образом отличаться от идеального квадруполя с гиперболическими стержнями.

Задача определения оптимального соотношения радиуса цилиндрических электродов r к "радиусу поля" r0 , т. е. оптимального значения для геометрического параметра y = r / r , имеет длинную историю [1–4]. Вначале предполагалось, что оптимальная величина γ соответствует конфигу- рации электродов, когда додекапольная компонента поля отсутствует: А6 = 0 . Поэтому в течение определенного времени разными исследователями предлагались различные соотношения γ , при которых достигается условие А6 = 0. Так, в классической книге по квадрупольной масс-спектрометрии [1] приводится величина γ= 1.148. Исходя из численных расчетов, Dayton и др. [2] также нашли γ = 1.148 . Denison получил значение Y = 1.1468 в работе [3]. Позже Lee Whiting, Yamazaki [4] и далее Reuben и др. [5, 6] окончательно установили с помощью точных математических методов, что полному отсутствию додекапольной гармоники поля A6 соответствует соотношение Y = 1.14511.

Как оказалось впоследствии, соотношение, при котором A 6 = 0, не является оптимальным для работы квадрупольного фильтра масс в верхней рабочей вершине диаграммы стабильности. После обнуления гармоники A ₆ на поведении заряженных частиц начинает сказываться влияние следующей по рангу гармоники A ₁₀ электрического поля и, как оказалось при более тщательных исследованиях, оптимальный режим реализуется, когда гармоники A ₆ и A ₁₀ отчасти компенсируют друг друга [9]. На основе моделирования формы массового пика Schulte и др. [7] нашли оптимальное значение γ= 1.10 , Gibson и Taylor определили Y = 1.12 - 1.13 [8], Konenkov и Douglas нашли, что оптимальное значение у = 1.128 - 1.130 [9].

Следует отметить, что оптимальное значение параметра γ зависит также и от режима, в котором используется квадрупольная ловушка либо квадрупольный масс-анализатор. Так, в работе [10] было впервые исследовано дипольное масс-селективное возбуждение колебаний ионов в линейной ловушке с круглыми электродами и было найдено, что в этом случае оптимальная величина для параметра у равна 1.14 - 1.16.

Используя подход, изложенный в [10], в данной работе исследуется влияние соотношения y = r / r на форму массового пика при квадрупольном масс-селективном возбуждении колебаний ионов. В частности, рассматриваются случаи, когда квадрупольное возбуждение создается:

• 1)    дополнительным ВЧ-напряжением;

• 2)    амплитудной модуляцией питающего напряжения;

• 3)    частотной или фазовой модуляцией питающего напряжения.

В случаях 2) и 3) следует ожидать повышения разрешающей способности прибора за счет созда- ния "островов стабильности" [11–17] поверх классической диаграммы стабильности квадрупольной ловушки. Само по себе использование квадрупольного возбуждения для создания островов стабильности для целей масс сепарации ионов уже было изложено ранее в ряде работ [11–17], однако исследование этого режима работы квадрупольной ловушки для масс-селективного возбуждения ионов и, самое главное, определение оптимального параметра γ , соответствующего данному режиму работы, осуществляется в данной публикации впервые.

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ, СОЗДАВАЕМОЕ КРУГЛЫМИ ПАРАЛЛЕЛЬНЫМИ ЭЛЕКТРОДАМИ

Для расчета формы массового пика или контура возбуждения будем использовать аналитическое описание электрического поля, формируемого круглыми электродами. Аналитическое описание поля позволяет в явной форме определить уравнения движения, которые подлежат численному интегрированию. Построение контура возбуждения предполагает расчет большого числа траекторий (вплоть до 20 000 для построения одного контура) и на большом интервале интегрирования (0–10 000 π ). В частности, решение такой задачи с помощью программы SIMION [24] потребовало бы значительно больших временных затрат, чем трассировка частиц при использовании рассматриваемого здесь аналитического описания для электрического поля, создаваемого четырьмя идентичными цилиндрическими параллельными электродами.

В данном исследовании используется оригинальный численный метод расчета амплитуд Аk гармоник электрического поля, генерируемых круглыми электродами, исходно предложенный в [18]. Распределение потенциала Ф(x,y), создаваемое четырьмя стержнями, для рассматриваемого симметричного расположения электродов можно представить в виде от

^{Ф (x,} y)= U base • Re Е ^AK ⁽ x + i У ) K ,          ⁽¹⁾

K = 0

где U _base — напряжение, прикладываемое к противоположным парам электродов; A_K — амплитуды пространственных гармоник порядка K ; x и y — поперечные координаты фильтра масс; i = V-1 .

Обозначим координаты zk = xk + iyk положения центра k -го электрода, k = 1,2,3,4 на комплексной плоскости z = x + iy. Тогда комплексный потенциал F (z) в точке z можно представить в ви- де бесконечного ряда [18]:

F ( z ) = £ F k ( z ), k = 1

где

F k ( z ) = C k o ln I----- k - | + ^ C kj

^V r )    j = 1

V ^z

r

^{- z}k

r — нормировочный множитель, равный радиусу цилиндрического электрода. Заметим, что здесь вместо полиномиальных мультипольных функций ( z - z_k ) j , связанных с центром координатной системы, использованы обратные мультипольные функции ( z - z_k ) j , связанные с центрами цилиндрических электродов. Нормировка на множитель

r

обеспечивает выполнение условия

r

< 1

для точек z , расположенных вне кругов, соответствующих цилиндрическим электродам. В результате рассматриваемый ряд (2) будет гарантированно сходиться за пределами цилиндрических электродов, причем достаточно быстро. Каждый член ряда (2) удовлетворяет уравнению Лапласа, а неизвестные коэффициенты C_k,j определяются из граничных условий^*)

Re F ( z )| s_k = ( - 1) ^{k + 1}; k = 1,2,...,4.       (3)

Конечно, при численных расчетах амплитуд A_K в формуле (2) приходится ограничиваться конечным числом m членов ряда 4

F ( z ) = £ F ^m ( z ), k = 1

m

F k” ( z ) = C k о ln( z - z_k ) + V C k, ( z - z k ) - ^Y .    (4)

j = 1

Однако, управляя числом членов ряда (4), можно эффективно управлять точностью расчета. Сравнивая между собой результаты расчета для разных m , можно определить абсолютное значение погрешности численного расчета поля:

а именно ( m + 1 ) -й член ряда (4), посчитанный исходя из выбора числа членов ряда равным ( m + 1 ) , является эффективной оценкой невязки для решения (4), построенного исходя из m членов ряда (4).

Определим на каждой из четырех окружностей S_k наборы пробных точек z_kj , k = 1,2, — , m + 1, чтобы число пробных точек было равно числу коэффициентов C_kj для формулы (4). Подставляя комплексные координаты z_k j в граничные условия (3), получим систему линейных уравнений относительно неизвестных коэффициентов C_k,j (вообще говоря, комплексных). Система линейных уравнений для коэффициентов C_k,j быстро решается любым подходящим численным методом, в результате конструируется явное аналитическое выражение для функций F ” ( z ) (уравнение (4)). Далее комплексная функция разлагается в ряд Тейлора в точке z = 0 (в центре электродной конфигурации), и тем самым в конечном итоге требуемая функция Ф ( x,y ) находится в виде ряда (1), разложенного по мультипольным функциям в явном виде.

Расчет нормированных весовых коэффициентов A_K осуществлялся с помощью программы для символьных вычислений Mathematica [23] версии 8.0. В качестве входных данных использовался безразмерный параметр у = r/r ₀ , заданный в виде конкретного числового значения. Выходным результатом вычислений служил ряд (1) для разложенного по мультипольным компонентам комплексного потенциала Ф ( z ) с конкретными числовыми значениями для коэффициентов A_K , рассчитанными программой. Впоследствии этот ряд использовался для задания в аналитической форме потенциала высокочастотного электрического поля на этапе трассировки заряженных частиц (см. далее). Например, для конфигурации электродов с у = 1.12 и у = 1.13 функции Ф ( z ) равны соответственно

Ф ( z ) = 1.0010814634648662 z ² +

+ 0.0016708907345140132 z ⁶ -

• -    0.0024238204705233756 z ¹⁰ -

• -    0.00030167992689260586 z ¹⁴ -

• -    0.000025183117402883926 z ¹⁸ -

• -    0.000001591780758486225 z ²² - —   (5)

Ф ( z ) = 1.001755743217267 z ² +

+ 0.0009993339876074956 z ⁶ -

- 0.0024353383877332023 z ¹⁰ -- 0.00029433623332515544 z ¹⁴ -- 0.000023874805634993886 z ¹⁸ -- 0.000001458303146264798 z ²² - ... (6)

По выражениям (5) и (6) явно видно, как проявляют себя для исследуемой геометрической конфигурации электродов пространственные гармоники: K = 2 (основная, квадрупольная), K = 6 (додекапольная), K = 10 (эксипольная) и гармоники высших порядков K =14, 18, 22, ….

Для обеспечения вычисления коэффициентов A K с относительной погрешностью не хуже 10 ^{- 15} оказалось достаточно использовать m = 50 муль-типольных функций в разложении (4). Следует отметить, что такая точность расчета поля с трудом достижима (если вообще возможна) с применением стандартных численных пакетов расчета электрических полей, не учитывающих специфику рассматриваемого электрического поля, а также не использующих возможность выполнения промежуточных арифметических операций с точностью, существенно превышающей разрядность процессора, как это сделано в данном случае.

УРАВНЕНИЯ ДВИЖЕНИЯ ИОНОВ В МУЛЬТИПОЛЬНЫХ ПОЛЯХ

ПРИ КВАДРУПОЛЬНОМ ВОЗБУЖДЕНИИ

По итогам выкладок, приведенных в предыдущем разделе, электрический потенциал Ф ( x,y,t ) , создаваемый четырьмя параллельными круглыми электродами линейной ловушки в случае подачи на электроды строго синусоидальных ВЧ-напря-жений, определяется как

to

^{ф (} x , y , t ) = V • Re £ A N

V N ² r 10 V • Re Z A.

^ N= 2

N

N x + i y

V r 0 ,

Г i y

V r 0

cosQ t

N

cosQ t ,

где V — амплитуда ВЧ-напряжений, приложенных к электродам; z = x+ i y — комплексная координата; r ₀ — радиус вписанной окружности между вершинами электродов; Ω — базовая частота высокочастотного квадрупольного напряжения; i = V-1 ; A N — амплитуда соответствующей пространственной гармоники поля. Как легко заме-

тить, в данном случае в выражении (7) учитываются только 3 гармоники поля — 2-я, 6-я и 10-я. Это связано с тем, что по итогам расчета следует, что для интересующих нас геометрических конфигураций гармоника A ₁₄ на порядок меньше, чем A ₁₀ , поэтому гармониками более высокого порядка N >  14 можно без опасений пренебречь.

В данной работе будут рассматриваться три способа достижения резонансного параметрического возбуждения колебаний ионов:

• (i)    использование добавочного квадрупольного ВЧ-напряжения [11, 12, 16, 17], когда напряжение на электродах имеет вид V cos О t + V ex cos to _ex t (где V _ex — амплитуда добавочного напряжения, ω _ex — частота добавочного напряжения);

• (ii)    амплитудная модуляция базового ВЧ-на-пряжения [13], когда напряжение на электродах имеет вид V ( 1 + m a cos to a t ) cos О t (где ma — относительный коэффициент амплитудной модуляции, ω_a — частота перестройки амплитуды ВЧ-напряжения по синусоидальному закону);

• (iii)    фазовая модуляция базового ВЧ-напряжения [14], когда напряжение на электродах имеет вид V cos ( О t + m f cos to f t ) (где m^ — относительный коэффициент фазовой модуляции, ω_f — частота перестройки фазы ВЧ-напряжения по синусоидальному закону).

Дополнительную свободу управления параметрическим возбуждением колебаний ионов дает тот факт, что можно варьировать начальный сдвиг фазы между рабочим ВЧ-напряжением и фактором, осуществляющим параметрическое возбуждение ионов, а также варьировать начальную фазу влета иона в высокочастотное электрическое поле.

Для указанных способов квадрупольного возбуждения потенциалы электрического поля, создаваемого в объеме устройства, записываются следующим образом:

Ф AD ( x,y,t ) = ( V cos ( О t + ф ) + V _ex cos ( tot + a ) ) x

X

r 10

Re Z A n

V N= 2

^N x^y I V r 0 J I

Ф _АМ ( x,y,t ) = V ( 1 + m a cos ( tot + a ) ) cos ( О t + ф ) x

x

⁴ 10

Re Z A n

v N =

N x^y I

V r 0 J J

Ф FM ( x,y,t ) = V cos ( Q t + m f cos ( rot + a ) + ф ) x

x Re

^ 10

Z An

^ N= 2

^N x + i y )

d 2 Y d ξ ²

= + ( q cos [ 2 ( £ - ^ o ) ] + q _e x COS [ 2 v£ +a ] ) x

V r o ) )

x Im

Z NA n ( X + i Y ) N - 1

N= 2

где для всех трех случаев введено унифицированное обозначение частоты ω и фазы α , контролирующих синусоидальные законы изменения рабочего ВЧ-напряжения, а также добавлена начальная фаза ϕ рабочего ВЧ-напряжения, соответствующая моменту влета иона в ВЧ-поле. На основании второго закона Ньютона уравнения движения по x и y координатам имеют вид

где начальная фаза (фаза влета иона) рабочего ВЧ-напряжения ϕ пересчитана в соответствующий сдвиг по оси безразмерного времени как

^ o =- Ф 2.

В случае амплитудной модуляции (9) уравнения движения имеют вид:

d² x     „ дФ ( x,y,t )

mi —- = - Ze---------, dt2            5x

d 2 X d ξ ²

- q ( 1 + m a cos [ 2 v^ + a ] ) cos [ 2 ( ^ - ^_o ) ]x

d² y     „ дФ ( x.y,t )

m, —= - Ze--------, i dt2             dy

x Re

Z NA n ( X + i Y ) ^N - 1

N= 2

где Ze — заряд иона ( Z — целое число зарядов, e — константа, соответствующая заряду электрона); m i — масса иона; Ф ( x , y , t ) — меняющийся во времени по соответствующему закону потенциал высокочастотного электрического поля, представленный в виде ряда по мультипольным гармоникам. Далее введем безразмерные переменные времени и координат и безразмерные параметры q , q _ex , ν :

d 2 Y d ξ ²

+ q ( 1 + m a cos [ 2 v^ + a ] ) cos [ 2 ( ^ - ^ _o ) ]x

x Im

Z NA n ( X + i Y ) ^N - 1

N= 2

При фазовой модуляции (10) питающего напряжения уравнения движения ионов имеют вид:

d 2 X d ξ ²

- q cos [ 2 ( ^ - ^ o ) + m f cos ( 2 v^ + a ) ]x

Ω t      x y        4 eV

2 ’ V V q ( m,/Z ) 12 r ’

4 eV _ex         ω

= ( m/Z jS? ’ ^v = a ’

x Re

Z NA n ( X + i Y ) ^N - 1

N= 2

,

d ^Y = + q cos [ 2 ( ^ ^- ^ o )

+ m f cos ( 2v^ + a ) ]x

x Im

где ξ — безразмерное время; X и Y — безразмерные координаты; q — безразмерный параметр, характеризующий рабочее ВЧ-напряжение; q _ex — безразмерный параметр, характеризующий добавочное ВЧ-напряжение; ν — безразмерная частота возбуждения.

Используя безразмерные переменные (12), преобразуем для случая добавочного квадрупольного напряжения (8) уравнения движения (10):

Z NA n ( X + i Y ) ^N"

N= 2

d² X d ξ ²

- ( q cos [ 2 ( £ - £ o ) ] + q _e x COS [ 2v^ + a ] ) x

x Re

Z Na n ( X + i Y ) N - 1

N= 2

Явное полиномиальное представление через переменные X и Y для выражений вида Re [ ( X + i Y ) ^N ] и Im [ ( X + i Y ) ^N ] позволяет запрограммировать быстрый и эффективно вычисляемый компьютерный код, что важно с учетом количества пробных траекторий, необходимых для вычисления характеристик работы рассматриваемой линейной ловушки (см. далее). Вычисление соответствующих выражений с помощью программы Mathematica выполняется элементарно и не требует сколь бы то ни было значительного времени (как компьютерного, так и времени самого исследователя), поэтому соответствующие формулы в данной работе не приводятся.

РАСЧЕТ ФОРМЫ МАССОВОГО ПИКА S ( q )

ПРИ КВАДРУПОЛЬНОМ ВОЗБУЖДЕНИИ

Основной характеристикой масс-селективного резонансного параметрического квадрупольного возбуждения является контур возбуждения, или форма массового пика S ( q ) [19, 20] (где масса ионов m , выступающая в качестве параметра, пересчитывается в безразмерный параметр q ~ 1/ m , характеризующий уравнение Матьё). Величина S численно равна доле ионов S ( q ) = N ex / N , достигших вершин электродов за время возбуждения n периодов ВЧ основного поля при данном значении параметра q . Здесь N _ex — число траекторий ионов, для которых x ( t ) ² +y ( t ) ² >  r₀ на интервале времени возбуждения [ 0, 2пп /Q] , а N — суммарное число траекторий ионов с различными начальными условиями, участвующими в моделировании при заданном значении параметра q . Начальные поперечные координаты и скорости ионов имеют распределения Гаусса, характеризуемые дисперсиями по координатам σ_x = σ_y , выраженные в единицах r ₀ , и дисперсией по скоростям o s ~4 - 10 ^{- 4} V t, выраженной в единицах гД / 2 , где T — температура ио вле

(13)–(18) через сдвиг ξ ₀ безразмерного времени, имела случайное равномерное распределение на периоде ВЧ-поля [ 0, п ] . Для определения наилучшей формы массового пика использовались следующие условия: q = 0.85 , v = в , ^_x = 0.01 r ₀, T = 1000 K, a = 0, n = 500. Программа расчета траекторий ионов (12)–(15) и построения контура возбуждения S ( q ) была реализована в среде программы для символьных вычислений Mathematica версии 8 [23].

Основными параметрами, влияющими на форму массового пика, являются параметр возбуждения q _ex , параметры модуляции m_a и m_f , частота возбуждения ν , которая зависит от рабочей точки q ₀ , время возбуждения n , а также соотношение γ= r / r ₀ . Выбор безразмерной частоты параметрического возбуждения ионов ν= ω / Ω определялся из условия v = e = k / P , k = 1,2, • ••, P - 1 для выполнения условия существования параметрического резонанса [12].

ВЛИЯНИЕ СООТНОШЕНИЯ γ=r / r ₀ НА ФОРМУ МАССОВОГО ПИКА

На рис. 1 представлены контуры параметриче-го резонансного квадрупольного возбуждения рабочей точке q ₀ = 0.862883 и относительной

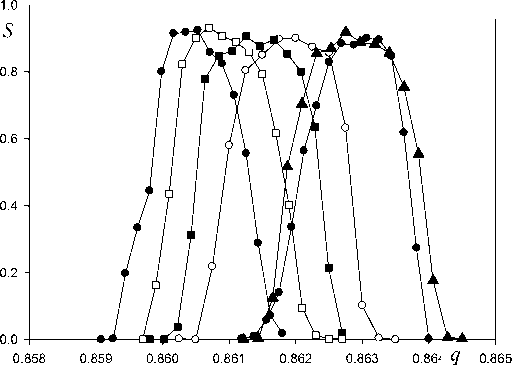
Рис. 1. Квадрупольное резонансное возбуждение колебаний ионов дополнительным ВЧ-напря-жением.

r/r 0 =1.11, R 0.5 =509, q ex =0.00160

r/r 0 =1.12, R 0.5 =444, q ex =0.00161

r/r 0 =1.13, R 0.5 =456, q ex =0.00162

r/r 0 =1.14, R 0.5 =477, q ex =0.001626

r/r 0 =1.15, R 0.5 =568, q ex =0.00163

q field ,      R 0.5 =420, q ex =0.00161

Контуры массового пика при различных значениях γ= r / r ₀ , q ₀ = 0.862883 , ν= ^ω = β = 4 / 5 ,

N = 500, n = 500 ВЧ-периодов

ω частоте возбуждения ν= = β= 4/ 5 для ряда значений r / r0 . Для каждого контура указаны требуемые значения параметра возбуждения qex M и разрешающая способность R0.5 =    = q /Δq , определенная по полувысоте массового пика. Ширина пика Δq находилась с помощью маркера. Погрешность вычисления величины Δq определялась настройкой маркера на заданную точку кривой S (q). В результате погрешность определения разрешающей способности R0.5 составила ±20 для условий рис. 1. Число траекторий на точку контура составляет 500, что достаточно для статистического сглаживания кривой S (q). Контур, помеченный черными треугольниками (qfield), соответствует идеальному полю и имеет R0.5 = 420±20 .

Контуры для идеального поля и для γ = r / r0 =1.11 приблизительно совпадают, однако разрешающая способность возрастает в последнем случае до R0.5 = 510. При этом проявляется нежелательный низкомассовый "хвост" пика. С увеличением соотношения γ контур см что гар чи когда форма контура симметрична и "хвосты" пиков наименьшие. При значении γ= 1.14 со стороны малых q начинает проявляться асимметрия пика и обнаруживается пьедестал. Это приводит к снижению изотопической чувствительности. Требуемое значение параметра возбуждения qex изменяется слабо с изменением соотношения γ в представленном интервале 1.10–1.15.

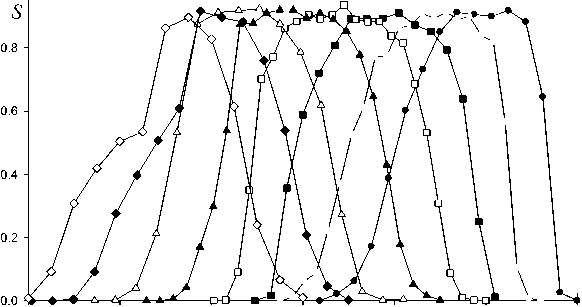
На рис. 2 показаны контуры возбуждения S ( q ) для различных значений γ= r / r ₀ для случая параметрического резонансного возбуждения колебаний ионов путем частотной или фазовой модуляции основного питающего напряжения. Данные контура характеризуют масс-селективность квадрупольного возбуждения, степень которой описывается разрешающей способностью R _0.5 .

Увеличение величины γ приводит к смещению массового пика в сторону малых масс по шкале масс. При r r ₀ = 1.10–1.11 правая сторона контура более крутая и левая сторона затянута, т. е. пики имеют низкомассовые "хвосты". При значениях r r ₀ = 1.12–1.13 разрешающая способность приблизительно равна R _0.5 = 450 , как и в случае идеального поля. При этом форма пика наиболее симметрична и имеет колоколообразный вид. При начинают проявляться низкомассовые хотя разрешающая способность не-растает. Результаты схожи со случаем я колебаний дополнительным ВЧ-1).

1.0

0.858          0.859          0.860          0.861

0.862          0.863          0.864

Рис. 2. Частотная модуляция основного питающего напряжения.

r/r 0 =1.10, R 0.5 =520, m f =0.0041

r/r 0 =1.11, R 0.5 =490, m f =0.0040

r/r 0 =1.12, R 0.5 =444, m f =0.00405

r/r 0 =1.13, R 0.5 =440, m f =0.00414

r/r 0 =1.14, R 0.5 =490, m f =0.00418

r/r 0 =1.15, R 0.5 =576, m f =0.0041

r/r 0 =1.16, R 0.5 =556, m f =0.00422

r/r 0 =1.17, R 0.5 =563, m f =0.004298

Контуры массового пика при различных значениях γ= r / r0 , q0 = 0.862883, n = 500 ВЧ периодов v = - = e = 4/5, ^ = 500, Ω

1.0

S

0.8

0.6

0.4

0.2

0.0

0 857

0 858   0 859   0 860   0 861    0 862   0 863   0 864

0 865 q

q field ,      m a = 0.00272, R 0.5 = 450

r/r 0 =1.10, m a = 0.00270, R 0.5 = 660

r/r 0 =1.11, m a = 0.00273, R 0.5 = 476

r/r 0 =1.12, m a = 0.00273, R 0.5 = 450

r/r 0 =1.13, m a = 0.00274, R 0.5 = 470

r/r 0 =1.14, m a = 0.00276, R 0.5 = 530

r/r 0 =1.15, m a = 0.00276, R 0.5 = 650

r/r 0 =1.16, m a = 0.00276, R 0.5 = 640

r/r 0 =1.17, m a = 0.00276, R 0.5 = 640

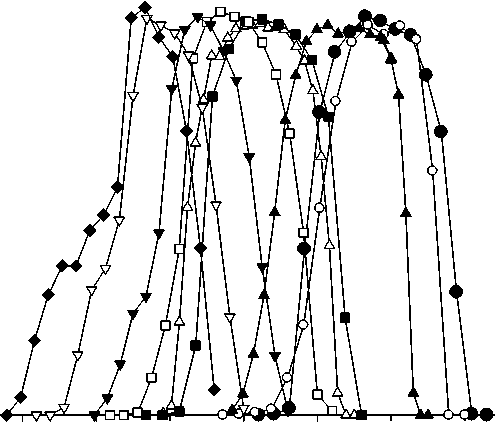
Рис. 3. Амплитудная модуляция ВЧ-напряжения.

Контуры масс селективного возбуждения при различных значениях γ = r / r ₀ , q ₀ = 0.862883 , v = to /Q = в = 4 / 5 , N = 500 , n = 500 ВЧ-периодов

На рис. 3 представлены результаты исследования влияния соотношения γ = r / r ₀ на форму массового пика для случая амплитудной модуляции ВЧ-напряжения. Как и ранее, контуры приблизительно совпадают при у = 1.10 c идеальным квадрупольным полем. Однако при у = 1.10 левая сторона массового пика затянута. Форма контура параметрического резонансного возбуждения наиболее совершенна — имеет колоколообразную форму и симметрична — при соотношении радиусов r / r ₀ = 1.12–1.13. При γ >  1.13 появляется низкомассовый "хвост" и форма пика несимметрична.

На рис. 4 для сравнения показаны контуры возбуждения при квадрупольном возбуждении (АМ — амплитудная модуляция, ν= β= 4/ 5 ) и при дипольном возбуждении [19] (DE, v = в /2= 2/5) в рабочей точке q0 = 0.862883. Для идеального поля разрешающая способность R0.5 приблизительно в 2 раза больше для дипольного возбуждения по сравнению с квадрупольным возбуждением. Заметим, что это не связано с тем, что при дипольном возбуждении ионы попадают только на два противоположных электрода, а при квадрупольном на четыре. Было проверено, когда регистрация осуществляется только на два электрода |х (t)< г0|, разрешающая способность прак- тически не изменяется при квадрупольном возбуждении.

Использование цилиндрических электродов более эффективно для дипольного возбуждения [19], когда разрешающая способность возрастает в 1900 / 470 , т. е. в 4 раза по сравнению с квадрупольным возбуждением для заданного времени резонансного воздействия ( n = 500 периодам ВЧ-поля).

ВЛИЯНИЕ ГЕКСАПОЛЬНОЙ И ОКТУПОЛЬНОЙ ПРОСТРАНСТВЕННЫХ ГАРМОНИК ПОЛЯ НА ФОРМУ МАССОВОГО ПИКА

В работах [21–22] показано, что наличие малых гексапольных полей (гармоника A ₃ ) [22] и окту-польных полей (гармоника A ₄ ) [21] при работе в верхней вершине с a = 0.237 и q ₀ = 0.706 может обеспечить разрешающую способность в несколько тысяч, несмотря на искажение поля. В этом случае необходима подача требуемой полярности напряжений на противоположные цилиндрические электроды.

Распределение потенциала в квадрупольном поле с малой добавкой гексапольной компоненты дается выражением

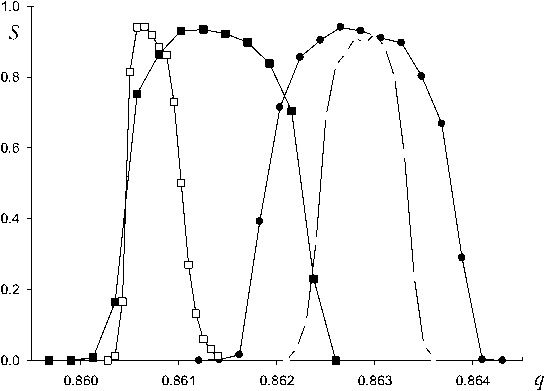
AM, m a = 0.00272, R 0.5 =450

DE, q ex =0.000139, R 0.5 =960

DE, r/r 0 =1.15, q ex =0.000139, R 0.5 = 1900

AM, r/r 0 =1.13, m a = 0.00274, R 0.5 =470,

Рис. 4. Контуры возбуждения для двух способов резонансного воздействия на ионы: квадрупольного с амплитудной модуляцией (АМ) и дипольного (DE) и для ловушки с гиперболическим и цилиндрическим профилями электродов

f 2 _ 2 A f 3 _ 12

Ф (X,y) - A y I+ A3 -----y I .(19)

FlFl

_ V ro    У V     ro

При добавке октупольной пространственной гармоники потенциал имеет вид

Ф ( X,y,t ) -

A ₂

f X ²

—

y ^{2 A}

V    r o     У

+A ₄

f X ⁴

— 6 X ² y ² + y ⁴'

V

⁴ r ₀

У

. (20)

Заметим, что уравнение (20) удовлетворяет уравнению Лапласа для произвольных значений A ₂ и A ₃ . Это означает, что можно подобрать такой профиль сечения электродов, чтобы обеспечить заданное значение амплитуд A ₂ и A ₃ . Полагая потенциал пары электродов Φ= ± 1В,

r ₀ = 1, находим уравнение профиля электродов, задающих квадрупольное поле с гексапольной A ₃ и октупольной A ₄ компонентами электрического поля:

± 1 -A 2 ( x ² — y ² ) + A 3 ( x ³ — 3 xy ² ) , (21)

± 1 - A 2 ( x ² — y ² ) + A ₄ ( x ⁴ — 6 x ² y ² +y ⁴ ) . (22)

На рис. 5 приведены профили электродов, генерирующие квадрупольное поле с амплитудой A ₂ = 1 и поля с амплитудами гармоник A ₃ = 0.02 и A ₄ = + 0.04 . При изменении знака коэффициента A ₃ структура электродов поворачивается на 90°.

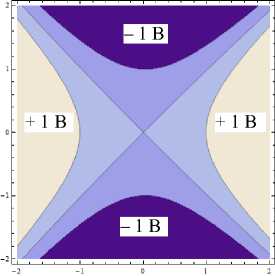
A 2 = 1, A 3 = +0.02

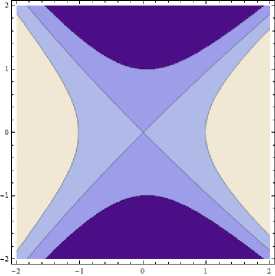
A ₂ = 1, A ₄ = +0.04

Рис. 5. Профили электродов, создающих квадрупольное поле с А ₂ = 1 и поля с дополнительными гармониками с амплитудами А 3 = 0.02 и А 4 = 0.04 при подаче на противоположные электроды напряжения V = ± 1В

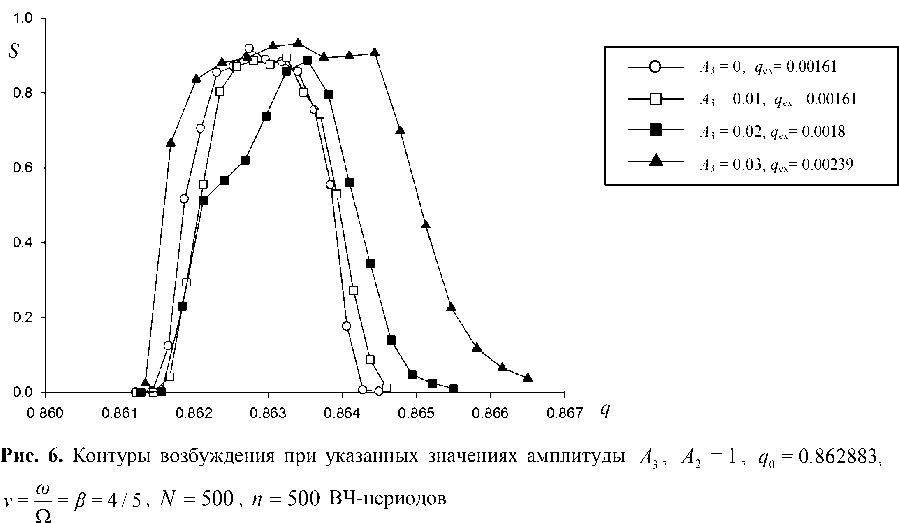
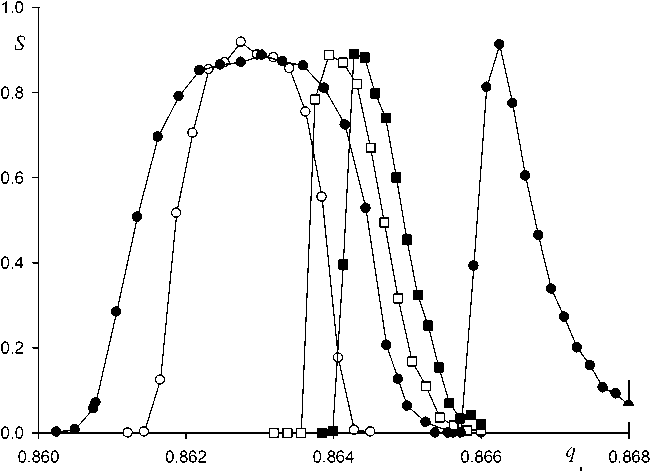
A 4 = 0, q ex = 0.00161, R 0.5 =420

A 4 = 0.0025, q ex = 0.0022, R 0.5 =270

A 4 = 0.004, q ex = 0.00235, R 0.5 = 800

A 4 = 0.005, q ex = 0.0026, R 0.5 = 1190

A 4 = 0.01, q ex = 0.0046, R 0.5 = 1060

Рис. 7. Влияние амплитуды А 4 октупольной компоненты поля на форму массового пика S ( q ). ν = β = 4/5 , n = 500 периодов ВЧ-поля, N = 500 траекторий на точку кривой S ( q )

На рис. 6 показаны контуры квадрупольного возбуждения для A3 = 0, 0.01, 0.02 и 0.03. С увеличением А3 требуемая амплитуда возбуждения возрастает. Практически изменение контура не наблюдается вплоть до значения A3 = 0.01. При A3 > > 0.01 контур деформируется, пик уширяется и появляется "хвост" со стороны высоких масс (больших значений q).

На рис. 7 иллюстрируется влияние на контур возбуждения S(q) величины амплитуды А4 окту-польной гармоники при квадрупольном возбуждении дополнительным ВЧ-полем с относительной частотой ν= β = 4 / 5 (q0 = 0.862883). Можно видеть, что при малых значениях А4 =0.0025 происходит уширение массового пика, при этом сохраняется хорошая симметричная форма. При увеличении А4 до значения 0.004 пик резко сужается и разрешающая способность достигает R0.5 = 800. При дальнейшем увеличении амплитуды А4 до значения 0.005 начинает проявляться затянутость пика в сторону увеличения параметра q, при этом происходит смещение контура по оси q. Таким образом, при добавке октупольной малой компоненты можно достичь увеличения разрешающей способности R0.5 приблизительно в два раза без существенного затягивания пика.

ВЫВОДЫ

Независимо от способа параметрического резонансного квадрупольного возбуждения путем амплитудной или частотной модуляции, а также использования дополнительного ВЧ-напряжения, оптимальное соотношение r / r 0 = 1.12–1.13, когда форма пика симметрична и проявление "хвостов" пиков относительно мало. Это соответствует результату [8], полученному Gibbson и др. для обычного режима работы в вершине a = 0.237, q = 0.7060 [1]. Наиболее эффективно использование круглых стержней для дипольного возбуждения при соотношении радиусов r / r 0 = 1.14–1.16 [19]. Возможно, такое аномальное различие связано с тем, что при квадрупольном возбуждении вынуждающая резонансная сила пропорциональна смещению иона ( F _ex ~ x ), а при дипольном возбуждении вынуждающая сила не зависит от положения иона.

Наличие "чистой" гексапольной компоненты электрического поля всегда ухудшает качество контура возбуждения вплоть до А ₃ = 0.01. Влияние октупольной гармоники поля на форму массового пика более сложно: при малых значениях 0 < A ₄ <  0.003 происходит уширение пика, а при A ₄ ≥ 0.004 разрешающая способность возрастает вдвое по сравнению со случаем идеального поля, однако при этом проявляется "хвост" со стороны больших масс.