Формальное представление модели реализации функций системной инженерии на основе принципа необходимого разнообразия структурных связей

В настоящее время принципы системной инженерии доведены до предметно-ориентированных стандартов, но проблема разработки системных моделей, соответствующих этим общим положениям требует применения нового математического аппарата и программных инструментариев.

Подобная системная задача решается в известной инженерной методологии CALS (Continuous Acquisitionand Lifecycle Support), где определены понятия объекта, производственной среды и жизненного цикла объекта. В работе предлагается развить данную методологию до моделей биз-нес-процессов, моделей среды их выполнения, жизненных циклов бизнес-процессов из необходимого условия управляемости Эшби.

Постановка задачи. Актуальным вопросом является повышение эффективности процессов обработки, передачи и использования данных и знаний кадрового резерва предприятий при их многостороннем анализе. В повышении эффективности важна заинтересованность как со стороны организации, обладающей кадровым резервом, так и со стороны организаций, вкладывающих средства в поддержание кадрового резерва. Видится целесообразным для построения модели функционирования данной системы воспользоваться положениями системной инженерии для дальнейшего автоматизированного управления кадровым резервом. Возникает проблема, связанная с использованием двух взаимосвязанных бизнес-процессов кадрового резерва и кадрового агентства (например, образовательные учреждения).

Модель реализации функций системной инженерии на основе принципа необходимого разнообразия структурных связей.

Рассматривая информационные объекты двух взаимосвязанных бизнес-процессов (на примере кадрового резерва и кадрового агентства), можно использовать наиболее распространенный в системной инженерии стандарт ISO/IEC 15288.

Данный стандарт классифицирует четыре группы процессов жизненного цикла системы: процессы предприятия, процессы соглашения, процессы проекта и технические процессы, которые могут быть представлены в виде «дерева» процессов (рис. 1).

Жизненный цикл системы

Процессы соглашения

---Поставка

Приобретение

Процессы            ( предприятия   )       \

Управление:

---Жизненным циклом

---Инфраструктурой

---Портфелем проектов

---Персоналом

---Качеством

---Знаниями

Процессы    \ проекта     )

Технические процессы

---Планирование

Поддержка

Измерение

Обеспечение качеством

Управление:

---Проектами

Решениями Конфигурацией Информацией Выполнением и контролем

Анализ БИ

---Потребности стейкхолдеров

---Системные требования

---Архитектура

Тактико-технические

требования

---Системный анализ

---Реализация, верификация,

интеграция Передача ---Валидация

Эксплуатация и

сопровождение

---Списание

Рис. 1. Процессы активностей стандарта ISO/IEC 15288

Процессы жизненного цикла стандарта ISO/IEC 15288 «Системная инженерия», такие как процессы предприятия, процессы проекта и технические процессы помогают эффективному формированию и применению систем, способствующих в достижении целей предприятия. А процессы соглашения представляют собой рабочие взаимоотношения путем заключения соглашений, вызывающие для нас наибольший интерес.

Используя формализацию, предложенную в [1], стандарта ISO/IEC 15288 «Системная инженерия», каждая стадия может быть представлена в виде категории процессов. При рассмотрении процесса соглашения причины и следствия могут быть использованы симметрично.

Так, процесс соглашения состоит из процесса приобретения и процесса поставки. Причем процесс симметричный, приобретающей стороной одновременно могут выступать обе стороны. Используя информационный подход для формализации предметной области, получаются первичными категории объектов и отношения между ними. Таким образом, система отношений может быть представлена множеством объектов предметной области и множеством отношений между ними.

Рассмотрим для моделирования данного процесса базовые положения теории категорий. Будем использовать следующие обозначения: процессы соглашения PS , процессы приобретения PS _pr , процессы поставки PS _po .

Выделим процессы соглашения PS , приобретения PS _pr и поставки PS _po в отдельные категорию и подкатегории, которые состоят из целей процесса, деятельности процесса и результата. Рассмотрим взаимодействие подкатегорий, внутри которых информационные объекты, в результате чего получается коммуникативный треугольник по категории и отдельным подкатегориям.

Согласно стандарту ISO/IEC 15288 «Системная инженерия» процесс соглашения состоит из процессов приобретения и процессов поставки [2].

Данная категория PS образует класс объектов с заданным отношением для любых пар ( PS , PS _pr ) и ( PS , PS _po ) , отношения которых определены множеством морфизмов: f ₁ , f ₂ , p ₁ , p ₂ .

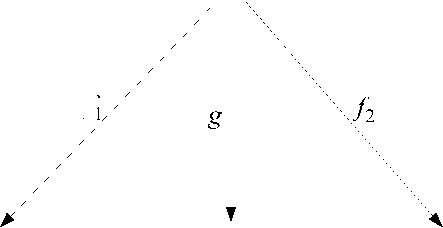
Рассматривая процессы соглашения PS как взаимосвязанные процессы приобретения PS _pr и поставок PS _po , процесс взаимодействия может быть представлен декартовым произведением g:PS → PS _pr ⊗ PS _po , где g является единственным морфизмом, выражающимся результатом процесса соглашения (рис. 2). Отметим, что эти операции соответствуют правилам формальной логики.

PS f1

PSpr "^   p 1    PSpr ® PSpo    p 2    PSpo

Рис. 2. Упрощенная схема коммуникативного треугольника процесса соглашения

Таким образом, процесс соглашения формализуется в виде морфизмов, обладающих следующими свойствами: результат взаимодействия информационных объектов может быть представлен декартовым произведением PS _pr ® PS _po с морфизмами p_x :PS _pr ® PS _po ^ PS ' _pr и p ₂ :PS _pr ® PS _po >e PS¹ такими, что для любого объекта PS с морфизмами f 1 : PS ^ PS _pr и f 2 : PS ^ PS _po существует единственный морфизм g:PS ^ PS _pr ® PS _po , при котором выделяется диаграмма в форме коммутативного треугольника, где ® - декартово произведение; g – морфизм, являющийся результатом процесса.

Рассмотрим следующую отдельную подкатегорию: процесс приобретения PS _pr , который складывается из трех составляющих (рис. 3):

• 1)    цели процесса приобретения;

  , p^r 8² } ;

  
  

• 2)    деятельности в процессе приобретения PS pr = { pr ²,

  ...

  
  

  3) результата процесса приобретения PS_pr = { pr ³ ,

  
  

  ...

  
  

  , p^r 7³ } .

  
  

g з e Hom( PSp„. , PS²_pr ) ^ PSp,_r ® PS ²_pr .

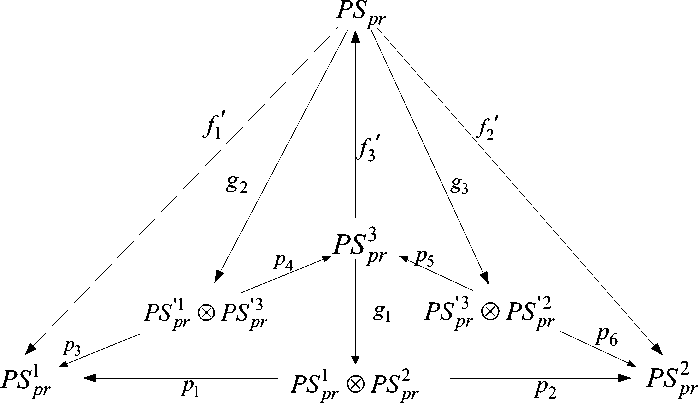
Рис. 3. Коммуникативный треугольник процесса приобретения

Взаимодействие информационных объектов PS1pr и PS2pr может быть представлено декартовым произведением PSxpr ® PS2pr с морфизмами p1 :PSxpr ® PS2pr ^ PS1r и p2 :PSxpr ® PS2pr ^ PSpr такими, что для любого информационного объекта PSpr с морфизмами f1' :PS pr → PS1pr и f2':PS pr → PS2pr, существует единственный морфизм g1:PS pr → PS1pr ⊗ PS2pr который определяется коммутативной диаграммой.

Аналогично рассматривается взаимодействие объектов с морфизмами p ₃ :PS ^' _p ¹ _r ⊗ PS ^' _p ³ _r → PS ^" _p ¹ _r и p ₄ :PS ^' _p ¹ _r ⊗ PS ^' _p ³ _r → PS ^" _p ³ _r , при котором для любого объекта PS _pr с морфизмами f ₁ ^' :PS _pr → PS ¹ _pr и f ₃ ^' :PS _pr → PS ³ _pr существует единственный морфизм g ₂ :PS _pr → PS ^' _p ¹ _r ⊗ PS ^' _p ³ _r , который определяется коммутативной диаграммой.

Таким же образом рассматривается взаимодействие объектов PS ^' _p ³ _r ⊗ PS ^' _p ² _r с морфизмами p ₅ :PS ^' _p ³ _r ⊗ PS ^' _p ² _r → PS ^" _p ³ _r и p ₆ :PS ^' _p ³ _r ⊗ PS ^' _p ² _r → PS ^" _p ² _r такими, что для любого объекта PS _pr с морфизмами f ₂ ^' :PS _pr → PS ² _pr и f ₃ ^' :PS _pr → PS ³ _pr существует единственный морфизм g ₃ :PS _pr → PS ^' _p ³ _r ⊗ PS ^' _p ² _r , который определяется коммутативной диаграммой.

В результате процесс приобретения может быть представлен в виде декартового произведения следующих проекций:

PS pr = ( PS ¹ pr ) ^' ⊗ ( PS ² pr ) ^' ⊗ ( PS ^' p ¹ r ) ^" ⊗ ( PS ^' p ³ r ) ^' ⊗ ( PS ^' p ³ r ) ^" ⊗ ( PS ^' p ² r ) ^" . (1)

Взаимодействие информационных объектов PS ¹ _po и PS ² _po может быть представлено декартовым произведением PS ¹ _po ⊗ PS ² _po с морфизмами p ₁ ^' : PS ¹ _po ⊗ PS ² _po → PS ^' _p ¹ _o и p ₂ ^' : PS ¹ _po ⊗ PS ² _po → PS ^' _p ² _o такими, что для любого информационного объекта PS _po с морфизмами f ₁ ^'' : PS _po → PS ¹ _po и f ₂ ^'' : PS _po → PS ² _po существует единственный морфизм g ^' :PS _po → PS ¹ _po ⊗ PS ² _po , который определяется коммутативной диаграммой в виде треугольника (рис. 4).

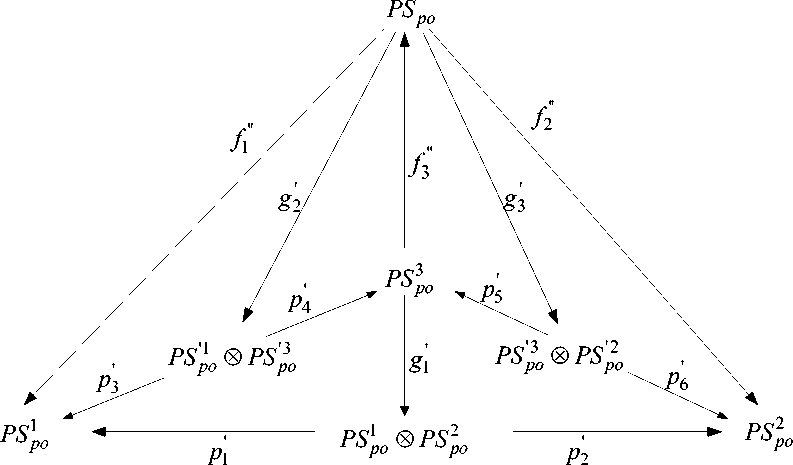
Рис. 4. Коммуникативный треугольник процесса поставки

Аналогично может быть рассмотрено взаимодействие объектов:

– PS ^{′ 1} _po и PS ^{′ 3} _po PS ^′ _p ¹ _o ⊗ PS ^′ _p ³ _o с морфизмами p ₃ ^′ : PS ^′ _p ¹ _o ⊗ PS ^′ _p ³ _o → PS ^′ _p ^′1 _o и p ₄ ^′ : PS ^′ _p ¹ _o ⊗ PS ^′ _p ³ _o → PS ^′ _p ^′3 _o такими, что для любого объекта PS _po с морфизмами f ₁ ^'' : PS _po → PS ¹ _po и f ₃ ^'' : PS _po → PS ³ _po существует единственный морфизм g ₂ ^' :PS _po → PS ^′ _p ¹ _o ⊗ PS ^′ _p ³ _o , представленный коммутативной диаграммой.

– PS ^′ _p ³ _o ⊗ PS ^′ _p ² _o с морфизмами p ₅ ^′ : PS ^′ _p ³ _o ⊗ PS ^′ _p ² _o → PS ^′ _p ^′3 _o и p ₆ ^′ : PS ^′ _p ³ _o ⊗ PS ^′ _p ² _o → PS ^′ _p ^′2 _o такими, что для любого объекта PS _po с морфизмами f ₂ ^'' : PS _po → PS ² _po и f ₃ ^'' : PS _po → PS ³ _po существует единственный морфизм g ^′ :PS _pо → PS ^' _p ³ _о ⊗ PS ^' _p ² _о такой, что диаграмма коммутативна.

В результате процесс приобретения может быть представлен в виде декартового произведения:

PS pо = ( PS ¹ pо ) ^' ⊗ ( PS ² pо ) ^' ⊗ ( PS ^' p ¹ о ) ^" ⊗ ( PS ^' p ³ о ) ^' ⊗ ( PS ^' p ³ о ) ^" ⊗ ( PS ^' p ² о ). (2)

При этом используется положение теории топосов, где показано, что любой из этих узлов может быть декомпозирован или показана связь с любым другим из узлов, представленных на рис. 4.

Результат может быть представлен в виде декартового произведения, причем если результатом является независимая величина, то он может быть промежуточным. Это позволяет выявить зависимость рекурсивной точки одной от другой. То есть если меняется цель, то возможно спрогнозировать результат, при этом информационные объекты представимы в виде категорий, а отношение перехода одной стадии в другую – в виде морфизмов.

Можем рассмотреть топос как категорию, которая обладает дополнительными свойствами, например, декомпозицией категорий. Путем формализации топоса, используя последовательное применение линейки или множества линеек преобразований, получаем диаграмму, приведенную на рис. 5.

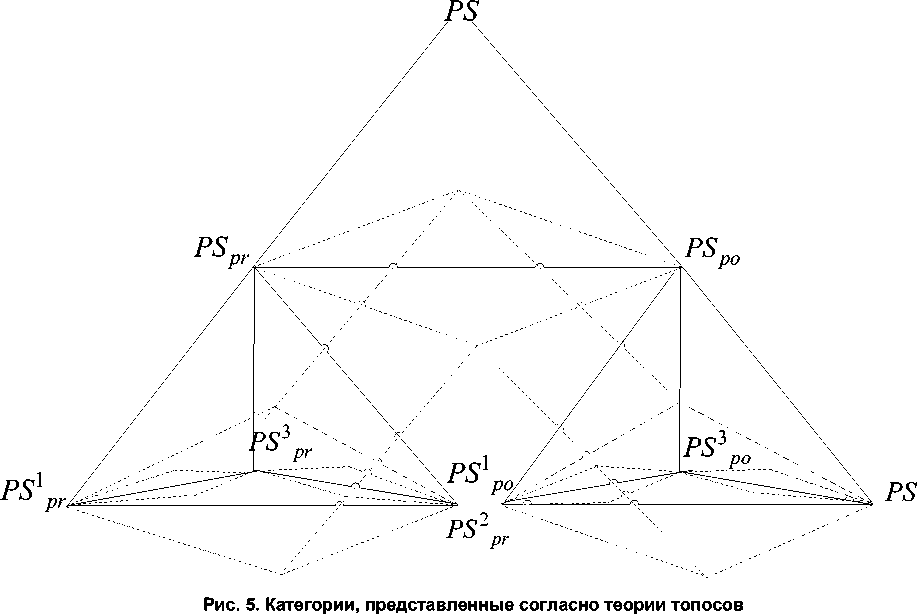
При рассмотрении процессов соглашения, где процесс приобретения PS _pr , процесс поставки PS _po , каждый из которых представим в виде категорий, взаимодействия объектов могут быть представлены совокупностью декартовых произведений:

PS pr ⊗ PS pо =〈 PS ¹ pr ⊗ PS ² pr , PS ^' p ¹ r ⊗ PS ^' p ³ r , PS ^' p ³ r ⊗ PS ^' p ² r , PS ¹ po ⊗ PS ² po ,

PS ^' p ¹ o ⊗ PS ^' p ³ o , PS ^' p ³ o ⊗ PS ^' p ² o 〉 .                                                                         (3)

Очевидно, что процесс соглашения в данном случае может быть представлен формулой

PS=〈(PSpr ⊗PSpo),(PSpo ⊗PSpr)〉.(4)

Аналогично процесс приобретения PS _pr может быть представлен формулой

PS pr = { 〈 ( PS ¹ pr ⊗ PS ² pr ),( PS ² pr ⊗ PS ¹ pr ) 〉 , 〈 ( PS ¹ pr ⊗ PS ³ pr ),( PS ³ pr ⊗ PS ¹ pr ) 〉 ,

〈(PS3pr ⊗PS2pr),(PS2pr⊗PS3pr)〉},(5)

а процесс поставки PS _po формулой

PS po = { 〈 ( PS ¹ po ⊗ PS ² po ),( PS ² po ⊗ PS ¹ po ) 〉 , 〈 ( PS ¹ po ⊗ PS ³ po ),( PS ³ po ⊗ PS ¹ po ) 〉 ,

〈(PS3po ⊗PS2po),(PS2po ⊗PS3po)〉}.(6)

Таким образом, взаимодействие между разными категориями может быть описано в виде функтора на основе представленных выше декартовых произведений.

В категории PS _pr любой объект будет отображаться в объекты категории PS _po следующим функтором:

f ∈ Hom( PS pr , PS po ) { f ∈ Hom( PS ¹ pr , PS ¹ po ), f ∈ Hom( PS ² pr , PS ² po ).

f ∈ Hom( PS ³ pr , PS ³ po )}.

Также описывается отображение объектов в категории PS _po :

g ∈ Hom( PS pr , PS po ) { g ∈ Hom( PS ¹ pr , PS ¹ po ), g ∈ Hom( PS p ² r , PS ² po ).

g ∈ Hom( PS ³ pr , PS ³ po )}.

Аналогично описывается и «декартово произведение», поскольку будем рассматривать его как новый объект:

f ∈Hom(PSpr⊗PSpo,PSpo), g∈Hom(PSpo,PSpo⊗ PSpro), f = g e Hom(PSpr ® PSpo, PSpo ® PSpro).

Таким образом, получаем, что объекты в категориях определяются взаимодействием функторов.

В данном случае можем использовать квадрат Декарта, где композиция представленных выше двух процессов, обозначенная g , является прямым отображением приведенного процесса соглашения на результат. Результат процесса может рассматриваться как композиция произведения целей и деятельностей. Получается еще один треугольник. При этом цель не может быть достигнута только одним путем. Применяя принцип необходимого разнообразия ЭШБИ [3], согласно которому не может быть одинаковых отношений между объектами, должны быть дополнительные пути достижения результатов, получаем дополнительные квадраты на диаграмме. То есть квадрат Декарта будет определяться принципом необходимого разнообразия ЭШБИ [4]. Данные диаграммы удовлетворяют положениям топоса, что позволяет вывести зависимость, например, этой точки от другой путем изменения результата, для этого определяем, что надо изменить в целях, что в деятельности, либо не изменяем цели, а только деятельность.

Выводы

Предложено правило синтеза самоорганизующейся структуры процесса соглашения, основанное на декомпозиции-композиции объектов-процессов путем логического сложения фракталов в форме коммутативных треугольников в квадраты Декарта и далее в Декартов многогранник. Показано, что в отношениях между элементами данных структур сохраняются правила формальной логики. Показана возможность построения ряда тождественных формальных алгоритмов контроля целостности структуры исходных процессов. Показана возможность параметрического контроля состояния процессов.