Формальное проектирование единичных технологий обработки деталей на металлорежущих станках

Ключевыми этапами создания и производства изделий в машиностроении является конструкторская и технологическая подготовка, от которых полностью зависит качество и себестоимость изготовления изделий, поскольку в процессе конструирования определяется «Что изготавливать?», а при проектировании технологии – «Как изготавливать?».

В современной мировой практике процессы конструирования и технологического проектирования являются уделом человека. Системы автоматизации проектирования (САПР) являются помощниками при выполнении поисковых и вычислительных процедур, тогда как синтез и принятие конструкторских и технологических решений выполняются инженерами, поскольку эти задачи пока остаются на уровне недетерминированных [1–4].

Отечественная и зарубежная методологии формирования технологических процессов выделяют два основных обобщенных подхода [3–5].

Первый из них – разработка с использованием технологических процессов на основе отработанных процессов-аналогов [2, 5–7]. Наиболее распространенными процессами-аналогами в России являются типовые технологические процессы (ТТП), предложенные профессором А.П. Соколовским в конце 1930-х годов [8]. Суть метода заключается в выборе детали, геометрически подобной рассматриваемой, для которой существует описание технологии изготовления, и использовании этой технологии в качестве аналога с незначительной доработкой. Для надежного распознавания и идентификации геометрических образов деталей или узлов А.П. Соколовский разработал многоуровневую иерархическую классификацию. Использование ТТП обеспечило значительное снижение трудоемкости и повышение эффективности машиностроительных производств в условиях выпуска часто меняющейся продукции. Впоследствии в США этот метод получил название групповых технологий (GT – group technologies ). Это подтверждается в опубликованной в 1984 году работе Нэнси Л. Хайера и Урбана Веммерлева: «Раннее использование GT было задокументировано в Советском Союзе в 1940-х годах. С тех пор она была внедрена во многих странах Европы и Азии, в основном в производственном секторе. Интерес среди американских производителей возник в середине 1970-х годов, и к настоящему времени многие крупные корпорации (такие как John Deere, Caterpillar, Lockheed, General Electric, Black & Decker и Cincinnati Milacron) воспользовались преимуществами GT или планируют программы GT» [9, с. 2].

В нашей стране дальнейшим развитием рассмотренного подхода явилась разработка технологических процессов с использованием заранее составленного набора технологических схем обработки, соответствующих не деталям, а их типовым геометрическим элементам, названным модулями (проф. Б.М. Базров) [7].

Использование уже разработанных технологий в качестве аналогов, т. е. прошлого производственно-технологического опыта, лежит в основе ряда отечественных автономных систем автоматизации проектирования технологических процессов (САПР ТП) в России, например, T-FLEX Technology, Вертикаль, TechCard, Technologi CS TRR, Timeline, Спрут-ТП и других [10].

За рубежом идея компьютеризации задач планирования производственных процессов, высказанная Нибелем (1965), была впервые реализована в 1976 году [3, 11]. Вышеупомянутые GT-технологии составили принципиальную основу первых систем компьютерного планирования процессов (CAPP – Computer aided Process Planning ) для подготовки планов изготовления деталей и изделий в производстве [12]. Процедура подготовки планов изготовления, иными словами «формирование технологии», заключается в выборе вариантов процессов, инструментов, оборудования из числа существующих и определении последовательности действий. Этот подход получил название Variant [3, 5, 6], что в отечественной литературе упоминается как вариантный (иногда вариативный).

Второй подход предполагает разработку технологии для каждого компонента, создаваемого «с нуля» без участия или с минимальным участием человека. Иными словами, он предусматривает создание оригинальных технологических процессов для каждой конкретной детали на основе формальных моделей с использованием доступных для реализации инструментов. В отечественных публикациях этот подход называется проектированием единичных технологических процессов, а в зарубежных – Generative (генеративный) [5–7].

В рамках генеративного подхода исследователи пытаются создавать системы САПР ТП и CAPP на основе инструментального арсенала формальных математических методов (однородные матрицы преобразования, торсор малых перемещений, дуальные кватернионы и т. д.), искусственного интеллекта, используя нейронные сети, генетические алгоритмы, теорию множеств и нечеткую логику, сети Петри и т. д. [3, 5, 6, 13, 14]. В некоторых случаях роль связующих элементов играют локальные эвристики [14, 15]. Однако недетерминизм в методах создания технологических процессов и их элементов пока не позволяет создавать полностью автоматические системы CAPP [3, 16].

Множественность и неоднородность подходов и методов, используемых исследователями для решения задач проектирования, свидетельствует об отсутствии обобщенной стратегии исследований в этом направлении. Анализ публикаций последних лет показывает, что при разработке

САПР ТП и CAPP значительное внимание уделяется формализации методов моделирования геометрических конфигураций с учетом их отклонений от идеальности. Особенно актуальными являются вопросы распознавания и идентификации геометрических объектов, а также расчета и оптимизации допусков при создании технологических процессов изготовления деталей и узлов [17-20].

Целью исследования является решение на теоретическом уровне одной из важнейших задач - формализации проектирования технологии обработки с использованием закономерностей и взаимосвязей между геометрической конструкцией детали и разрешимыми процедурами ее изготовления.

Исследования авторов показали, что современные инструменты традиционной геометрии имеют проблемы, которые приводят к невозможности однозначного описания геометрических схем для генерации структуры реальных деталей машин [2, 21].

Для решения этих проблем использованы методы и инструментарий геометрии неидеальных объектов, в которой порождение, существование, взаимодействие и трансформация объектов описывается в шестимерном пространстве с двойной метрикой (линейной и угловой) [2, 21].

Результаты исследования изложены в виде принципов формального проектирования технологии изготовления заданной геометрической конфигурации деталей на металлорежущих станках. Представлен оригинальный подход, обеспечивающий в шестимерном геометрическом пространстве решение двух краеугольных проблем, связанных с генерацией элементарных поверхностей и порождением геометрических структур объектов [2, 21].

Излагаемые результаты могут служить основой разработки программного обеспечения САПР ТП и CAPP с высокой степенью автоматизации вплоть до автоматического проектирования технологических процессов обработки деталей на металлорежущих станках. Кроме того, оно может служить одной из фундаментальных предпосылок для разработки автоматических металлообрабатывающих станков, способных изготавливать детали в широком диапазоне геометрических конфигураций.

Основные задачи проектирования технологии обработки деталей

Функциональные характеристики детали определяются, с одной стороны, заданным набором свойств (физических, механических, химических, электрических, магнитных и др.) материала, с другой - требуемой геометрической конфигурацией и точностью её исполнения. Тогда проектирование технологических процессов изготовления деталей сводится к решению двух краеугольных задач [2, 21, 22]:

• 1)    обеспечение заданных свойств материала детали;

• 2)    обеспечение геометрической конфигурации детали с регламентированной точностью.

В общем случае процесс изготовления детали можно рассматривать как конечное ненулевое множество дискретных технологических процедур1 (МТ), на котором определен порядок следования. Считается, что в ходе выполнения процедур, принадлежащих множеству МТ, исходная заготовка преобразуется в готовую деталь в соответствии с заданными параметрами.

С учетом разнохарактерности технологий, применяемого оборудования, инструментов и оснащения множество технологических процедур (МТ) можно разделить на два конечных непере-секающихся множества [2, 21]:

• -    множество процедур М^Тт-.{Тт₁, Тт₂, ...Тт_п }, обеспечивающих заданные свойства материала детали (твёрдость, прочность, коррозионная стойкость, намагниченность и пр.), например, отжиг, закалка, нормализация и т. д.;

• -    множество процедур М^Тд: {Тд₁ ,Т д ₂ , .Т д_к }, в результате выполнения которых формируется геометрическая конфигурация детали (геометрический облик и заданная точность), например, фрезерование плоскости, сверление отверстия, точение цилиндрической поверхности, нарезание резьбы и пр.

При этом М^т = M^Tm U М^Тд Ф 0 и М^Тт П М^Тд = 0.

Тогда принципиальная схема создания (проектирования) единичного технологического процесса представляется в виде, как показано на рис. 1, и включает в себя выполнение следующих этапов:

• 1)    формирование множества технологических процедур обеспечения свойств материала M^Tm : { Тт₁, Тт₂, ■■■ Тт_п };

• 2)    формирование технологических процедур получения геометрической конфигурации детали М^{Т{ {} Тд 1 , Т д ₂ , ... Тд_к ^};

• 3)    объединение множеств М^Тт и М^Тз и определение порядка следования элементов этих

множеств, т. е. последовательности выполнения всех технологических процедур.

Как показано на рис. 1, порядок выполнения 1-го и 2-го этапов, т. е. формирования множеств М^Тт и М^Тз, может быть произвольным, однако выполнение третьего этапа возможно только при наличии результатов двух первых.

Фактически определение порядка следования технологических процедур (3-й этап) завершает генерирование технологических решений, дальнейшая разработка заключается в привязке технологических процедур к конкретным рабочим местам и формировании производственных потоков.

По мнению авторов, рассмотренные три этапа содержат непосредственное решение технологических задач, а остальные, например, привязка технологических процедур к производственному оборудованию, формирование установов, компоновка операций и др., следует отнести к организационно-логистическим задачам управления производством.

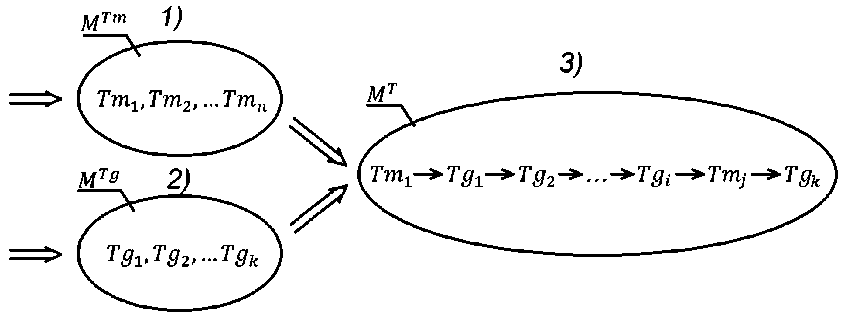
Рис. 1. Общая схема решения задач при разработке технологического процесса

Fig. 1. General scheme for solving problems in the development of machining processes

Технологии обеспечения свойств материалов, как правило, сопровождают процесс изготовления детали начиная от исходного состояния заготовки. При этом рассматриваются механические, электрические, магнитные, оптические физические, химические и другие свойства материала.

В процессе получения детали из заготовки свойства материала могут изменяться. С этой целью в технологическом процессе предусматриваются технологические процедуры изменения свойств материала. К ним относятся термические (отжиг, отпуск, нормализация и т. д.), химикотермические (цементация, азотирование, нитроцементация и пр.), магнитные (намагничивание или размагничивание), процедуры нанесения покрытий, электрохимической обработки и др. Для разработки процедур формирования свойств материала широко используются методики проектирования, основанные на применении отработанных на практике типовых технологий.

Если абстрагироваться от необходимости изменения свойств материала, то проблемы проектирования технологии будут ограничены поиском способов получения заданной геометрической конфигурации детали. В реальном производстве немалое количество деталей, изготавливаемых на металлорежущих станках, не требует изменения свойств материала заготовки при изготовлении. Такие ситуации характерны при обработке деталей на многооперационных станках с ЧПУ.

В этих случаях из схемы разработки технологического процесса (см. рис. 1) исключаются 1-й и 3-й этапы, а проектирование технологического процесса заключается в формировании технологических процедур отделения (срезания) материала от заготовки таким образом, чтобы получилась геометрическая конфигурация, полностью соответствующая заданной.

Необходимо отметить два важных, но принципиально разных класса технологических процедур, выполняемых при обработке деталей резанием [2, 21].

К одному из них относятся процедуры, заключающиеся в «срезании» части материала заготовки, в результате чего получаются поверхности определенной формы. В соответствии с ГОСТ 3.1109-822 эти процедуры принято называть технологическими переходами. Заметим, что любая из этих процедур приводит к изменению геометрической конфигурации детали.

Другой класс объединяет процедуры, заключающиеся в ориентации формообразующих движений инструмента таким образом, чтобы формируемая на технологическом переходе поверхность располагалась относительно имеющихся на заготовке (реальных) поверхностей в соответствии с заданными требованиями. Действующий ГОСТ 21495-763 использует термин «установка», который определяется как «Базирования и закрепления заготовки или изделия». Следует отметить, что в результате выполнения этих процедур геометрическая конфигурация детали остается неизменной, а ГОСТ 3.1109-82 относит эти процедуры к вспомогательным переходам.

Таким образом, основными задачами проектирования технологического процесса обработки деталей резанием для получения заданной геометрической конфигурации является формирование двух непересекающихся множеств технологических процедур [2, 21, 22]:

• 1)    множество процедур формообразования и обработки поверхности, которые обеспечивают отделение материала от заготовки и получение заданной формы поверхности (ФП);

• 2)    множество процедур ориентации обрабатываемых поверхностей (формообразующих движений режущего инструмента), которые обеспечивают заданное взаимное расположение поверхностей (ВРП).

Первая задача. Процедуры формообразования и обработки любой поверхности⁴ представляют собой механическое отделение или так называемое срезание части материала от заготовки для получения заданной формы поверхности. Их проектирование заключается в поиске следующих решений:

• 1)    кинематика формообразования – производящие траектории движений и форма режущего лезвия (в плане);

• 2)    материал режущей части инструмента;

• 3)    параметры, характеризующие передний ( γ ) и задний ( α ) углы режущего лезвия инструмента;

• 4)    глубина резания ( t );

• 5)    скоростные характеристики резания ( V – скорость, S – подача);

• 6)    мощность резания ( N ).

Вторая задача . Процедуры ориентации обрабатываемых поверхностей относительно реально существующих поверхностей заготовки⁵ не предусматривают какое-либо изменение состояния заготовки. Главной их задачей является ориентация совокупности формообразующих движений в геометрическом пространстве заготовки таким образом, чтобы после выполнения обработки рассматриваемой поверхности последняя заняла положение, строго соответствующее заданным на чертеже линейным и угловым размерным связям [2, 21].

Если объединить результаты решения указанных задач, т. е. связать между собой и упорядочить полученные процедуры, как показано на рис. 2, в итоге сформируется пошаговая принципиальная схема технологического процесса обработки детали с максимальным уровнем дифференциации.

На рис. 2 цифры в кружочках обозначают номера изначально не существующих обрабатываемых поверхностей детали ( part`s surfaces ), символы в квадратиках обозначают реально существующие поверхности заготовки ( workpiece`s surfaces ), а цифры в квадратиках указывают на использование в качестве ориентиров (технологических баз) уже обработанных к текущему моменту поверхностей детали.

Процесс объединения процедур формообразования обрабатываемых поверхностей и процедур их ориентации относительно формообразующих движений инструмента заключается в фор- мальной идентификации по номеру обрабатываемой поверхности. При этом важно учитывать, что порядок выполнения процедур формообразования поверхностей может быть произвольным, но для выполнения процедур ориентации существуют строго определенные варианты последовательности их выполнения, приводящие к разрешимости задачи обработки всех требуемых поверхностей детали [2, 21, 23].

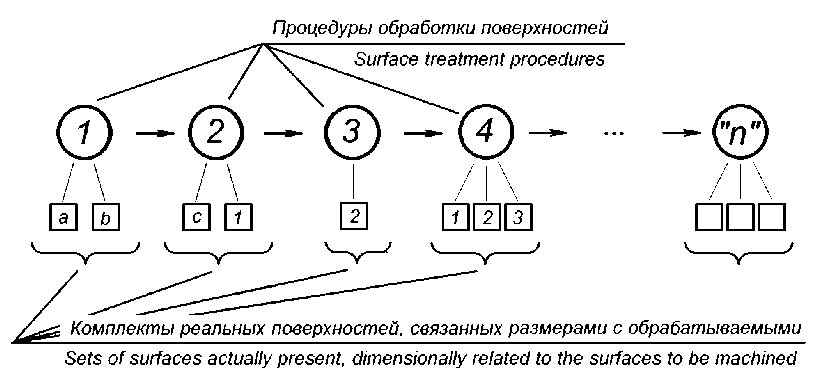
Рис. 2. Принципиальная схема технологического процесса обработки детали

Fig. 2. Schematic diagram of the sequence of the technological process for machining a part

Для формализации решения изложенных задач необходимо определить и описать принципиальные законы порождения геометрических конфигураций для реальных деталей.

Хотя со времен Евклида развитие геометрии насчитывает более 23 столетий, до сих пор остается проблемным создание формальных правил и методик построения технологического процесса «вырезания» из заготовки детали (геометрического объекта) с заданной геометрической конфигурацией в пределах регламентированных отклонений. Причинами отклонений размеров и формы реальных деталей являются упругие и температурные отклонения заготовки, инструмента, станка и приспособлений, погрешности перемещения рабочих органов, а также погрешности измерения [7, 8, 21, 24]. Кроме того, существуют погрешности, связанные с геометрическими параметрами изготавливаемой конфигурации, особенно со схемами задания размерных линейных и угловых связей, которые определяют взаимное расположение поверхностей [2, 21, 25].

Используемые в инженерной практики методы, приемы, инструменты, основываются на положениях современной аналитической геометрии, которая, по сути, формализует описание идеальных геометрических конфигураций и их элементов [2, 21, 26, 27]. Вершиной развития автоматизации проектирования считаются CAD, CAM, CAE и пр. системы, в основе которых лежат математические ядра трехмерного твердотельного геометрического моделирования, которые по факту являются лишь инструментом, при этом проектные решения вырабатывает и принимает инженер [10, 14, 16].

Определенная степень абстрагирования от реальности является характерной чертой математического представления геометрической конфигурации объектов. Однако практика применения математического инструментария для описания материальных технических объектов, свидетельствует о наличии фундаментальных проблем, не разрешимых в рамках существующих положений геометрии. С одной стороны, геометрические формы и конфигурации реальных объектов материального окружения имеют расхождения с отождествляемыми математическими и графическими образами, а с другой – геометрические преобразования идеальных моделей существенно разнятся с закономерностями взаимодействий неидеальных геометрических объектов в реальной природе [2, 21, 22].

Исследования авторов показали, что инструменты геометрии неидеальных объектов решают проблемы однозначного описания, а также порождения конфигурации деталей в шестимерном геометрическом пространстве [2, 21].

Геометрически деталь можно представить как некую часть материального вещества, нахо- дящегося в твёрдом состоянии, и в то же время как замкнутую часть пространства, ограниченного сочетанием конечного множества поверхностей. Вкратце рассмотрим основные положения геометрии неидеальных объектов и принципы существования и порождения их геометрической конфигурации.

Геометрическое пространство

Геометрическое пространство ℍ (home) представляет собой область (факторное пространство), допускающую порождение, существование и взаимодействие полного разнообразия реаль- ных или виртуальных неидеальных геометрических объектов G. Размерность пространства опре- деляется шестью независимыми параметрами (степенями свободы), которые представлены двумя тройками ортонормированных векторов (линейные и угловые).

Для определения угловых положений объектов в рассматриваемой геометрии введено понятие углового вектора (∝⃗), который представляет собой угловую величину (угол), измеренную в плоскости между двумя элементами геометрического объекта или объектов (рис. 3). Траектория углового вектора лежит в плоскости вращения и представляет собой дугу или окружность. На- правление углового вектора совпадает с направлением вращения или поворота [21].

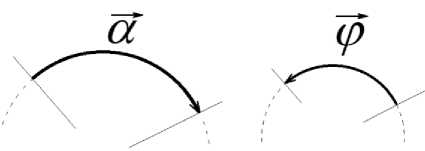
Рис. 3. Примеры визуализации углового вектора

Fig. 3. Examples of angle vector visualization

Одна из троек представляет собой три упорядоченных некомпланарных линейных вектора ( ⃗ X , ⃗ У , ⃗_z), а другая – три угловых вектора ( ∝⃗ X , ∝⃗ , ∝⃗ _z) с аналогичными свойствами [2, 21]. Каждая тройка векторов характеризуется своей метрикой, поэтому рассматриваемое геометрическое пространство имеет двойную метрику (линейную и угловую).

Связь между линейными и угловыми векторами показана на рис. 4. Угловые векторы ∝⃗ , ∝⃗ , ∝⃗ располагаются во взаимно перпендикулярных плоскостях, которые, в свою очередь, перпендикулярны соответствующим линейным векторам ⃗ X , ⃗ У , ⃗_z.

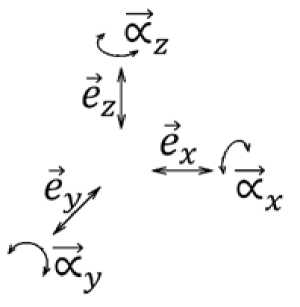
Рис. 4. Связь угловых и линейных векторов

Fig. 4. Relationship of angular and linear vectors

Для измерения линейных и угловых величин в геометрии неидеальных объектов используются инструменты нечеткой арифметики [28]. В данном контексте нечеткое число вида a ± Δ представляется двумя параметрами, первый из которых ( a ) определяет детерминированную составляющую, а второй (∆) – недетерминированную (стохастическую) величину ее возможного отклонения.

Значения линейного и углового размеров записываются как I = ± 3 a_t и a = ± 3 ^aa соответственно, где I^м и a^M – математическое ожидание линейного и углового размеров, а °l и O_a – среднеквадратичное (стандартное) отклонение этих случайных величин.

Геометрический объект представляется как нечеткое замкнутое подпространство с ненулевым объемом, ограниченное конечным множеством k (k ≥ 1) пересекающихся поверхностей, однозначно расположенных друг относительно друга. Конкретное взаимное расположение и ориентация поверхностей представляется связной шестимерной структурой (схемой) отношений между поверхностями, образующими геометрическую конфигурацию. При этом поверхности, линии и точки не являются геометрическими объектами, а рассматриваются как элементы геометрического объекта. Основными элементами для создания и определения геометрической конфигурации объекта являются поверхности [2, 21].

Поверхность рассматривается как граница, разделяющая две различные среды. В общем слу- чае множество поверхностей § (surfaces) включает в себя полное множество нечетких гладких бесконечных многообразий. Поверхность - это базовый элемент, т. е. «базовый кирпичик» для построения конфигурации объекта. Из всего многообразия выделяют три вида специальных поверхностей, которые относятся к элементарным: плоскость ( ), круговой цилиндр ( ) и сфера ( 5 s). К элементарным поверхностям относятся поверхности, которые могут быть образованы кинематически с помощью двух независимых элементарных производящих линий [2, 21].

Линия рассматривается как результат пересечения нечетких поверхностей произвольной формы, как показано на рис. 5. При этом линии рассматриваются как элементы кинематического порождения поверхностей. Среди множества нечетких линий ( ) можно выделить элементарные линии: прямую ( ) и окружность ( ). Элементарные линии, в свою очередь, ассоциируются с двумя типами векторов: линейными (е) и угловыми (ос) [2, 21].

Точка является результатом пересечения трех поверхностей и представляет собой вспомога- тельный элемент в виде нечеткого сферического пространства в месте пересечения. Положение в указанном пространстве математического ожидания i-й точки определяется тремя линейными координатами ( ⃗, ⃗, ⃗ ), а диаметр сферы c учетом нулевого математического ожидания характеризуется величиной стандартного отклонения [2, 21].

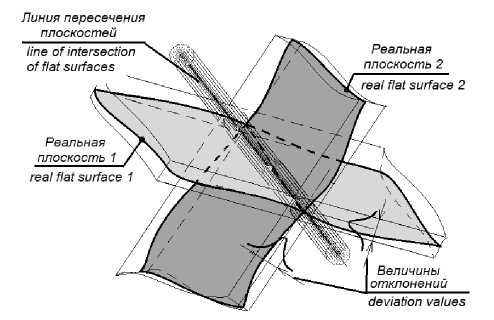
Рис. 5. Образование линии

Fig. 5. Line generation

Исследования авторов показали, что инструменты геометрии неидеальных объектов решают проблемы однозначного описания конфигурации деталей в шестимерном геометрическом пространстве.

Геометрическая конфигурация объекта определяется очертаниями границ, разделяющих объект и окружающую среду. Границы представляются набором взаимно ориентированных пересекающихся поверхностей. Иными словами, геометрическая конфигурация объекта определяется составом, т. е. набором поверхностей, а также структурой, т. е. набором значений пара- метров их взаимного расположения.

Формально геометрическая конфигурация объекта описывается парой множеств G (S , D ): 1) непустое конечное множество поверхностей S: ^ ,s₂ , ..,s_k}, т. е. VS (S £ 0), определяющее состав элементов; 2) конечное множество необходимых и достаточных отношений (угловых и линейных размерных связей) между поверхностями , определяющее структуру геометрической конфигурации. В шестимерном пространстве пару множеств G (S , D) удобно представить в виде шести плоских графов, в которых вершины соответствуют поверхностям (состав), а ребра - множеству размерных отношений между поверхностями (структура) [2, 21].

Множество D может быть пустым (D = 0) только в том случае, когда состав объекта определяется одной поверхностью (S = 1) из числа замкнутых, например, сферой, тором и т. д. [2, 21]. В общем случае множество D: {D ёх, Dёу, Dёг, D*^, D^y , DXz] получается объединением не-пересекающихся подмножеств размерных отношений в каждом измерении, т. е., например, D = DU Dsy U DSz U D °* U D *у U D *[ while Dё* П DёУ П DSz П D** П D*у П D^ = 0. Тогда структура геометрического объекта представляется в виде шести независимых наборов отноше- ний в пространстве размерностей ex, еу, ez,Kx,Ky,Kz. Например, для измерения ех связь между поверхностями запишется как

⃗ :    ⃗ ,   ⃗ ,…,   ⃗ ,…,   ⃗  , где ⃗

- бинарное отношение

⃗        ⃗                                           ⃗          ⃗     ⃗ между отображениями поверхностей s^* и s^* в направлении ех, т. е. d* = (s,x , s? , , i Ф j. Ана логично записываются содержимые подмножеств Dsy , DSz, D*^ , D^y, D^ [2, 21].

Создание геометрического объекта начинается с произвольного расположения первой (любой) базовой поверхности в шестимерном пространстве. Формально положение каждой из них можно представить единичным вектором S { ex, ey, ez,OCx,oCy,oCz}. Тогда горизонтально расположенная плоскость (рис. 6а) описывается в виде 5р{0,0,1,1,1,0}, вертикальный цилиндр (рис. 6b) -S с{1,1,0,1,1,0}, а сфера (рис. 6с) - 5s{1,1,1,0,0,0}, где единица обозначает наличие связи в соответствующем измерении, а нуль - её отсутствие.

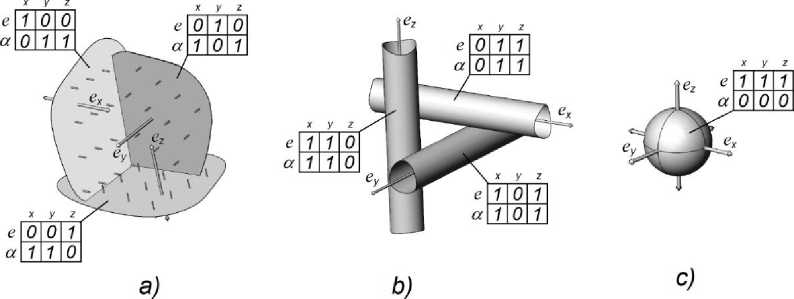
Рис. 6. Представление положений элементарных поверхностей в ортонормированном шестимерном пространстве: a) плоскость; b) цилиндр; c) сфера

Fig. 6. Representation of positions of elementary surfaces in orthonormalized six-dimensional space: a) plane; b) cylinder; c) sphere

Весьма примечательно, что плоскость всегда определяется одним линейным и двумя угловыми измерениями (см. рис. 6а) а любая цилиндрическая поверхность - двумя линейными и двумя угловыми измерениями (см. рис. 6b). Для определения положения сферы имеет смысл фиксация только трех линейных измерений (см. рис. 6c) [2, 21]. На рис. 6 в шестиклеточных таблицах единицы обозначают необходимость наличия размерной связи (метрики), нулевые значения свидетельствуют о невозможности связывания (отсутствия метрики) в рассматриваемом измерении, а стрелки указывают направления линейных векторов e_x, e_y, e_z .

Порождение геометрической конфигурации объекта

Если перед началом построения (порождения) геометрической конфигурации объекта отсутствуют какие-либо ориентиры (другие объекты или поверхности), то исходное геометрическое пространство может быть представлено нулевыми значениями во всех шести измерениях ( ^СХ — 0, ^СУ — 0, ^CZ — 0, ^ОХ— 0, ^0Су— 0, °^z— ⁰⁾.

Любая последующая добавленная поверхность должна быть связана с исходной поверхностью в тех измерениях, которые совпадают с «пространственным портретом» первой поверхности. На рис. 7 показан пример формирования координат пространства в процессе порождения геометрической конфигурации. Для отдельно стоящей плоскости «пространственный портрет» определяется тремя имеющими смысл измерениями (одним линейным и двумя угловыми) [2, 21].

Изначально разместим в геометрическом пространстве бесконечно протяженную плоскость 1 произвольной ориентации, как показано на рис. 7а. Символом X обозначим направление любого линейного вектора, направленного по нормали к плоскости. Тогда «пространственный портрет» плоскости, представленный в виде шестиклеточной таблицы (см. рис. 7а), будет содержать единицы в измерениях e_x, оС у , oc_z, которые свидетельствуют о том, что плоскость 1 является ориентиром в указанных направлениях для размещения и «относительной привязки» в пространстве других поверхностей. Иными словами, пространство задано координатами плоскости, т. е. плоскость 1 определила задание координат е_ж, О_у, oc_z.

Добавление любой следующей поверхности требует наличия размерной связи (или связей) с указанием задаваемой величины (величин). Например, в результате добавления плоскости 2, перпендикулярной плоскости 1, как показано на рис. 7b, получаем направление линейных векторов Y. При этом плоскости 1 и 2 связываются угловым размером 90° ± 20' в направлении Z, так как шестиклеточные таблицы рассматриваемых поверхностей требуют фиксации параметра ocz (см. рис. 7b). В результате дополнительно определяются исходные ориентиры для измерений еу и осж. Отметим, что поэлементное логическое сложение (дизъюнкция) шестиклеточных таблиц рассматриваемых поверхностей характеризует определённость измерений геометрического пространства. Как видно на рис. 7b, в результате сложения таблиц остаточная неопределенность имеется только в измерении ez, что соответствует значению «ноль» в таблице после выполнения дизъюнкции.

80±0,05

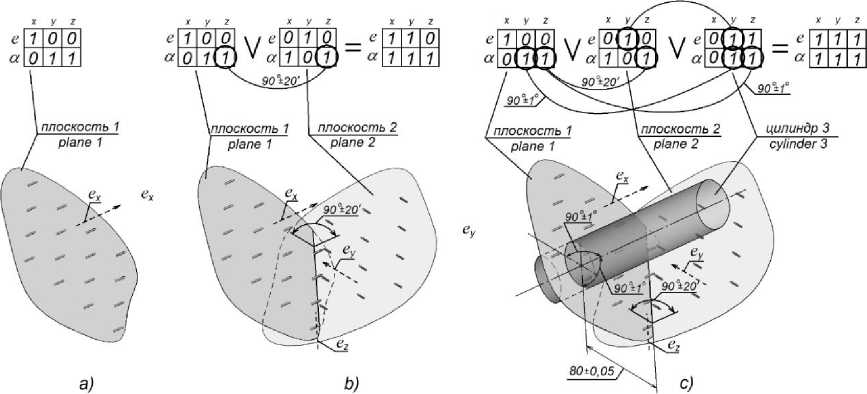
Рис. 7. Формирование ориентиров пространства в процессе порождения геометрической конфигурации Fig. 7. Formation of spatial landmarks when a geometrical configuration is generated

Следующей добавим бесконечно протяженную цилиндрическую поверхность 3, расположенную перпендикулярно плоскости 1 (рис. 7с). Тогда плоскость 1 и цилиндр 3 необходимо связать двумя угловыми размерными связями в измерениях ос_у и oc_z.Эти размеры заданы величинами 90 ° ± 1 ° , как показано на рис. 7с. Вместе с тем шестиклеточные таблицы плоскости 1 и цилиндра 3 содержат единицы в линейном направлении е_у , что свидетельствует о необходимости наличия линейного размера (80 ± 0,05 мм), связывающего эти поверхности. Как видно на рис. 7с, в результате логического сложения элементов шестиклеточных таблиц плоскостей 1, 2 и цилиндра 3 получена таблица, все элементы которой равны единице, что означает, что для каждого из шести измерений пространства задан как минимум один ориентир, т. е. для дальнейшего построения геометрической конфигурации сформировано пространство с полностью определенными ориентирами и системой координат будущей детали. При этом система координат детали является индивидуальной и не привязывается ни к какой общей базовой системе координат. Далее любая поверхность присоединяется к уже существующему набору размерными связями в соответствии с её «пространственным портретом».

Таким образом, по мере добавления размерных связей формируется структура (схема) геометрической конфигурации. Эта схема является уникальной (единственной и неповторимой) для каждого конкретного геометрического объекта и может быть эффективно использована для формального распознавания отличий геометрических конфигураций объектов. Также эта структура является информационной основой для формального определения множества возможных вариантов схемы последовательной обработки всех поверхностей детали [2, 21–23].

Проектирование технологических процедур обработки

Как было сказано выше, основными задачами создания технологического процесса получения заданной геометрической конфигурации детали G (S , D ) является проектирование процедур формообразования для всего набора поверхностей к-й детали S^к и процедур взаимной ориентации поверхностей в ходе обработки, т. е. пространственной структуры поверхностей D^k.

Проектирование процесса обработки детали фактически реализует вышеизложенную схему порождения (вырезания) геометрической конфигурации объекта. В качестве исходной заготовки рассматривается бесконечное геометрическое шестимерное пространство с неоднородной метрикой (линейная и угловая). Результаты технологического проектирования представляются в виде двух множеств:

• -    множество возможных вариантов формообразования для каждой поверхности S¹ рассматриваемой детали в виде технологических процедур обработки T^s: { Т/, Т^, ...Т^ };

• -    множество разрешимых вариантов схем порождения геометрической конфигурации (технологических процедур Т ° :{ t^t,. —> tq> —> tw }), обеспечивающих заданное взаимное расположение поверхностей детали.

Условия формального проектирования структуры технологического процесса:

• -    исходно заданная геометрическая конфигурация детали G (S , D ) является целостной, т. е. содержит перечень поверхностей (S) с указанием параметров для каждой из них и множество необходимых и достаточных размерных связей (D ) между поверхностями;

• -    предполагается, что обработка любой поверхности детали выполняется за один технологический переход, при этом количество проходов не ограничивается;

• -    исходный набор размерных связей в каждом из шести измерений ( ~е_х, ~е_у, ~e_z, oc_x, ос у , ос_г) может быть представлен плоским графом-деревом, т. е. связным ацикличным графом;

• -    в процессе обработки детали выдерживаются только исходно заданные размерные связи (линейные и угловые), т. е. в ходе проектирования технологии исключается любой перерасчет размерных цепей;

• -    в качестве исходной заготовки используется бесконечное геометрическое пространство, и задача обеспечения взаимного расположения поверхностей детали решается при отсутствии ориентиров для привязки к окружающему пространству;

• -    проектирование и определение размерных связей между поверхностями заготовки и детали выполняется после выбора рабочего варианта технологической структуры.

Проектирование процессов формообразования поверхностей

В основе порождения поверхностей в геометрии неидеальных объектов лежит кинематический метод, когда образование поверхности происходит в результате взаимодействия двух несовпадающих по направлению производящих (порождающих) линий, т. е. движения одной линии (образующей) относительно другой (направляющей) [2, 21].

Для любой элементарной поверхности существует как минимум две свободные координаты, которые не влияют на ее ориентацию в пространстве⁶. В шестиклеточных таблицах (см. рис. 6) эти координаты обозначены нулями. В соответствии с установленными закономерностями в рассматриваемом пространстве любой парной комбинации свободных координат однозначно соответствует пара независимых порождающих линий, образующих данную поверхность. Причем свободные линейные координаты соответствуют прямым линиям, параллельным линейным векторам ~е_х, ~е_у, ~e_z , а угловые координаты - окружностям с угловыми векторами к_х, О у , oc_z [2, 21].

Например, на рис. 7а шестиклеточная таблица для плоскости 1 содержит нули в координатах е_х, е_у и oc_z, т. е. эти координаты не определяют положение плоскости. Тогда множество парных комбинаций равно трем: 1) e_x and ву , 2) e_x and о, 3) ву and oc_z. Здесь первая пара производящих линий состоит из двух прямых взаимно ортогональных линий, а две другие включают одну прямую, расположенную вдоль оси X (или Y), и одну окружность относительно оси Z. Учитывая обратимость элементарных поверхностей, т. е. замену образующей на направляющую и наоборот, каждая пара производящих будет образовывать две схемы генерации рассматриваемой поверхности [2, 21].

Рассмотренный пример показывает, что для каждого типа элементарных поверхностей существует однозначное правило определения полного набора схем формообразования, представленных парами образующих линий. Установлено, что любой паре образующих линий строго соответствуют четыре метода обработки (непрерывный след, непрерывное копирование, дискретный след, дискретное копирование) [2, 21]. Под методом формообразования (получения формы) поверхности условимся понимать сочетание любой пары производящих линий с одним из указанных методов обработки. Отметим, что в результате удаления материала резанием на поверхности формируется характерного вида рельеф шероховатости, однозначно соответствующий рассмат- риваемому сочетанию [2]. Тогда мощность набора методов формообразования для плоскости определяется как |sp|=24, для цилиндрической поверхности |sc| =8, а для сферы |ss|=8.

Получение поверхностей любой сложности формы достигается преобразованием элементарных производящих линий с использованием алгоритмов формирования параметрических поверхностей Безье [29].

Таким образом, каждому элементу множества поверхностей конструкции любой детали S : { ^1 , S^ ,…, $k } (k – количество поверхностей) в точности соответствует один элемент множества технологических процедур обработки T^s :{ T^ , ^2 ,… ?k }. Другими словами, между формами поверхностей детали и технологиями их обработки существует биективное отношение, т. е. f : ↔ T^s [2, 21].

Формирование структуры процесса обработки детали

Более сложная взаимосвязь была установлена между структурой геометрической конфигурации конструкции: D : { D^ , ^2 ,…, Dy } (v – количество размерных отношений) и набором технологических схем, обеспечивающих относительную ориентацию поверхностей при обработке j^D :{ Tf , ?2 ,… Tw } (w – количество допустимых технологических схем).

Результаты исследований показывают, что для любой конструкции детали с правильно заданной структурой размерных связей ( Df ) существует уникальный набор вариантов структур технологических процессов, которые гарантированно обеспечивают заданное относительное положение поверхностей T^ : , ^2 ,…, ^£q ,…, tw } , ( Tj^D ∈ 'pD ). Реализация каждого варианта ( ^Q ) из этого набора гарантированно приведет к результату, заданному конструкцией детали, с учетом допусков на взаимное расположение поверхностей [2, 21].

Рассмотрим пример формирования структур процесса механической обработки. На рис. 8а показана геометрическая конфигурация детали, состоящая из шести плоскостей (P1, P2, P3, P4, P5, P6), одной цилиндрической поверхности (C1) и заданного набора размерных связей, определяющих их взаимную ориентацию.

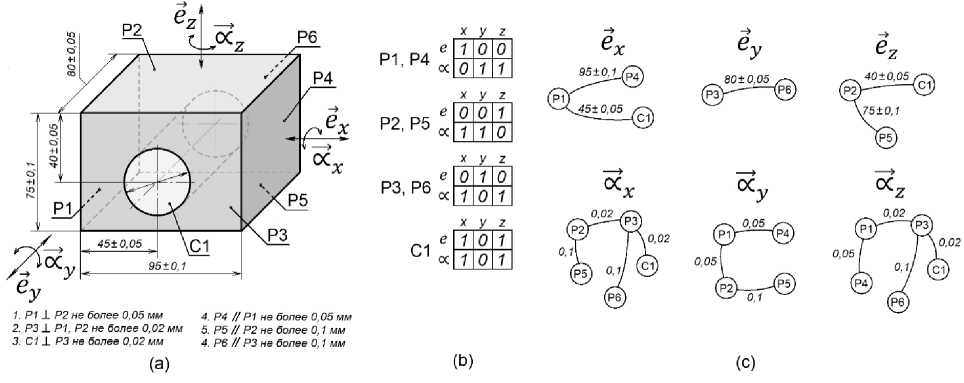
Рис. 8. Геометрическая конфигурация объекта: a) изображение детали; b) координаты положения поверхностей; c) графы размерных отношений

Fig. 8. Geometric configuration of the object: a) part image;

• b) surface arrangement tables; c) dimension relationship graphs

Положение поверхностей в пространстве представляется в виде шестиклеточных таблиц (рис. 8b). Заданные линейные и угловые размерные связи между поверхностями (см. рис. 8а) отображаются на графах смежности (рис. 8с) для каждого из шести измерений ( ⃗x, ⃗У, ⃗z,∝⃗x,∝⃗У,∝⃗z). Набор вершин каждого графа смежности определяется единицей в соответствующей размерности всех шестиклеточных таблиц. Например, в размерности ⃗ x единицы имеют поверхности P1, Р4 и C1, а в размерности ⃗ – только поверхности P3, Р6 и т. д. (см. рис. 8b). Ребрами графа смежности (см. рис. 8с) являются заданные на чертеже размерные связи (см. рис. 8а). Одним из важнейших правил, обеспечивающих однозначность и целостность геометри- ческой конфигурации детали, являются связность и ацикличность (отсутствие циклов) каждого графа, как показано на рис. 8с.

Формирование структуры технологического процесса моделируется как «вырезание» части пространства путем последовательного расположения формообразующих движений инструмента, которые однозначно соответствуют заданной взаимной ориентации поверхностей (см. рис. 8a).

Тогда первая произвольно расположенная поверхность задает часть координат, соответствующих ее характеристикам (см. рис. 8b), относительно которых «строится» геометрическая структура объекта. Учитывая, что моделирование можно начинать с обработки любой поверхности объекта, количество корневых вариантов структуры технологического процесса равно количеству поверхностей из общего состава.

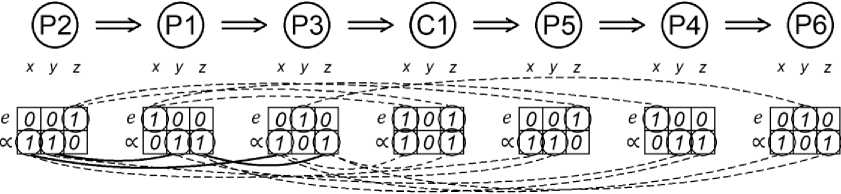
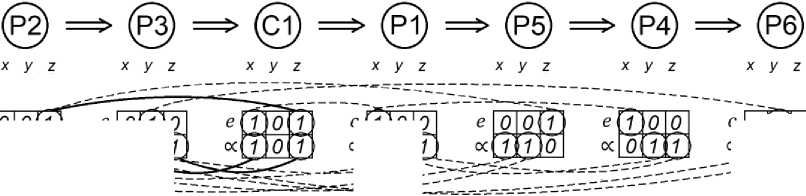
На рис. 9 показаны два разрешимых производных варианта структуры технологического процесса с первой обрабатываемой поверхностью P2. Под разрешимостью структуры технологического процесса понимается структура, обеспечивающая обработку множества заданных поверхностей детали. Номера поверхностей указаны в кружочках, а порядок их обработки указан стрелками (см. рис. 9). Снизу в соответствующих поверхностям шестиклеточных таблицах единичные элементы соединены сплошными и пунктирными линиями, которые отражают линейные и угловые размерные связи, показанные на рис. 8а и 8с.

Как видно на рис. 9а, первая обработанная плоскость P2 является ориентиром в каждом из трех измерений "е^ос^оС у . Исходя из заданных размерных связей (см. рис. 8с), в качестве следующей поверхности можно рассматривать альтернативы Р1, или Р3, или Р5 или С1. Рассмотрим обработку поверхности P1, которая связана с P2 угловым размером ( ! ) в измерении « ^ (см. рис. 8a и 8с). После обработки поверхность P1 определяет ориентиры еще для двух измерений е_х и oc_z геометрического пространства. Следующий шаг позволяет однозначно ориентировать поверхность P3, связанную с поверхностями Р2 и Р1 угловыми размерами ( ! ) в измерениях ос_х и oc_z соответственно (рис. 8a и рис. 8b). В результате этих шагов поверхности Р2, Р1 и Р3 определили ориентиры во всех шести измерениях, включая линейные ( "е_х = 1, ~е_у = 1, ~e_z = 1, а_х= 1, ос_у= 1, ∝⃗ = 1), хотя между собой эти поверхности связаны только угловыми размерами (на рис. 9а обозначены сплошными линиями).

а)

Ь)

Рис. 9. Визуализация структуры технологического процесса обработки детали: a) и b) варианты

Fig. 9. Visualization of the part machining process structure: a) and b) variants

е

К0Ш

е о °C 7 о7

е О к 77'7

е

0	1.	0
Л	0!	'1'

Дальнейшее моделирование обработки поверхностей выполняется в соответствии с наличием достаточного количества размерных связей для однозначной ориентации рассматриваемой поверхности. Для рассматриваемого случая следующей обрабатываемой может быть любая из оставшихся поверхностей (Р4, Р5, Р6 или С1), поскольку каждая из них связана необходимыми и достаточными размерами (на рис. 9а показаны пунктирными линиями).

Еще один вариант структуры технологического процесса с начальной обрабатываемой поверхностью P2 показан на рис. 9b. Здесь последовательно обрабатываются поверхности Р2, Р3 и С1, которые сформировали геометрическое пространство детали с полностью определенными ориентирами. В рассмотренном примере оба варианта приводят к разрешимости задачи, т. е. к обработке полного набора поверхностей с гарантированным достижением заданного относительного положения поверхностей с учетом допусков на размеры. Дальнейшая обработка осуществляется по аналогии с предыдущим вариантом.

Варианты технологической структуры с начальной вершиной Р2 не ограничиваются рассмотренными выше и могут быть продолжены. Совокупность всех разрешимых вариантов структуры технологического процесса с единой начальной поверхностью будем называть порождающей ветвью. Пример порождающей ветви с начальной вершиной показан на рис. 10. Двойными стрелками обозначены направления основных путей, приводящих к разрешимости задачи, одинарная стрелка указывает на ответвления, которые не приводят к изменению разрешимости.

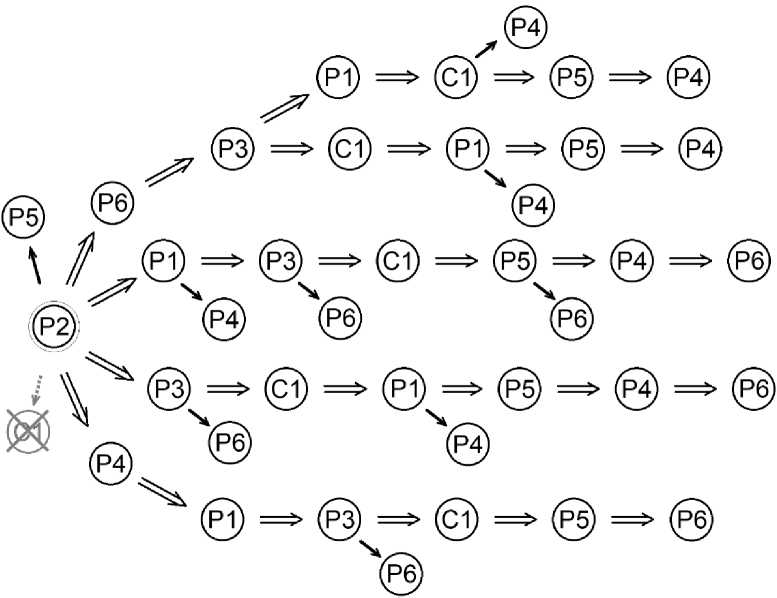
Рис. 10. Порождающая ветвь с начальной вершиной Р2

Fig. 10. Generating branch with initial vertex P2

На рис. 10 видно, что следующей после обработки первой поверхности (Р2) может быть поверхность из числа Р1, Р3, Р4, Р5 или Р6. Единственной поверхностью, которая не может быть обработана после поверхности Р2, является поверхность С1, поскольку в измерении ∝⃗ X нет прямой размерной связи между Р2 и С1 (см. рис. 8с).

Для получения полного множества разрешимых вариантов технологической структуры необходимо смоделировать остальные порождающие ветви, в которых исходными поверхностями являются P1, P3, P4, P5, P6, и C1.

Рассмотренные положения и приведенные примеры демонстрируют наличие формальных правил генерирования множества всех возможных вариантов технологических процедур обработки поверхностей практически любой сложности, а также порождения множества вариантов технологических структур, обеспечивающих взаимную ориентацию поверхностей обрабатываемой детали.

Целью обработки деталей на металлорежущих станках является получение заданной геометрической конфигурации детали. Поиск формальных методов проектирования процессов обработки связан с неразрешимостью однозначного представления геометрической конфигурации реальных объектов и закономерностей их порождения в парадигме геометрий, использующих трехмерное линейное векторное пространство.

В качестве формальной основы для решения этих проблем предлагается геометрия неидеальных объектов с шестимерным пространством, имеющим две метрики (линейную и угловую). Рассмотренная геометрия обеспечивает принципиальную возможность формально генерировать порождение геометрических конфигураций объектов и их элементов. Приведенные примеры демонстрируют существование правил формальной генерации как элементарных поверхностей, так и полного набора технологических структур, гарантированно обеспечивающих заданные параметры взаимного расположения поверхностей.

Наборы поверхностей и отношения между ними определяют индивидуальную структуру геометрической конфигурации для каждого конкретного объекта. Эта индивидуальность может быть эффективно использована для формального распознавания геометрических объектов.

Представленные материалы позволяют утверждать о существовании строгих соответствий между конструкцией детали и технологией ее обработки при условии, что ее геометрическая конфигурация правильно и последовательно представлена в шестимерном пространстве. Таким образом, геометрия неидеальных объектов может служить фундаментальной основой для формальных теорий создания оригинальных технологических процессов их обработки, а также конструирования механизмов и их деталей. В свою очередь, становится возможным создание ядер геометрического моделирования в шестимерном пространстве, что позволит разрабатывать САПР и системы автоматизированного проектирования с высокой степенью автоматизации вплоть до автоматического проектирования технологических процессов обработки деталей на металлорежущих станках.

1. Stavropoulos P., Bikas H., Avram O., Valente A., Chryssolouris G. Hybrid subtractive–additive manufacturing processes for high value-added metal components. Int J Adv Manuf Technol, 2020, vol. 111, pp. 645–655.