Formation of optimum temperature graph of paper web warming
Автор: Anatoliy Zhuchenko, Evgeniy Cheropkin, Liudmyla Osipa, Su Jun
Журнал: International Journal of Intelligent Systems and Applications @ijisa
Статья в выпуске: 11 vol.10, 2018 года.
Бесплатный доступ
To date, the requirements for the quality of paper products are increasing. At the same time, the most common trend in recent years is improving the resource and energy conservation of all technological processes. From the point of view of specialists in the field of paper industry in technological process of production on a paper machine, the greatest attention must be paid to the drying of a paper web. This process is the most expensive and decisive for a large number of quality parameters of finished products. In order to satisfy these requirements, it is necessary to implement a system of optimal control for this technological process. The first and one of the most important parts of the development of such system is the formation of a criterion for the optimal control and calculation of the optimal mode of operation of the first stage of drying - the heating of a paper web. For this purpose, the problem of calculating the optimal temperature graph of heating the paper web in the drying section of a paper machine is considered. Proposed quality control criterion ensures the maintenance of the parameters of finished products within the limits defined by the standard. Established limitations on the dynamics of temperature change on each drying cylinder and the final values. The calculation of the optimal temperature schedule is made by taking into account the characteristics of the material, the changes in the parameters of heat and mass transfer, which are functional dependences on the temperature of the paper web. The formulas for calculating the temperature of the paper at the exit from each drying cylinder and the free movement sections are based on the data on partial pressure on the surface of the paper web and in the environment. Results of the work are presented in the form of a step-by-step algorithm. Implementation of the developed algorithm ensures uniform heating of the paper web and reaches the optimum temperature for effective removal of moisture.
Paper machine, drying section of a paper machine, quality parameters of paper, optimal temperature graph, quality control criterion, algorithm for calculating optimal temperature graph, system of optimal control of heating a paper web
Короткий адрес: https://sciup.org/15016541
IDR: 15016541 | DOI: 10.5815/ijisa.2018.11.03
Текст научной статьи Formation of optimum temperature graph of paper web warming
Published Online November 2018 in MECS
In the modern electronic world, the pulp and paper industry does not lose its weight.
According to world statistics, amounts of paper production, after several years of decline, it has begun to show a positive dynamics of change [1]. Paper machine (PM) is a key technological element in the production process of paper. It represents a multi-stage process of converting cellulose or wasting paper into finished paper products.
Among all stages of production at PM, it is especially worthwhile to allocate the drying part, which is the main consumer of material and energy resources in the entire technological scheme of production. Its task is to dewater the paper web to the state of the finished product.
The initial moisture removal begins in the pressed part by a mechanical method. After reaching the maximum allowable value, further dewatering with this method leads to the internal structure destruction of the paper structure and negatively effects on quality of finished products. After that the paper web enters the drying part. To dry the moisture content of the material, it depends on the efficiency of the press part and can range from 60 to 75%. After drying, it can fluctuate between 5 and 10%.
It usually spend 30-40% out of all material and energy resources in this work. The drying part of a paper machine (PM) consists of cylinders arranged in two rows in a chess order, which is heated by a pair from the inside.
Paper web moved from the upper cylinder passes the free movement area to the bottom, and then reach the next top and so throughout the length of the drying part. At the same time, there is an increase in the temperature of the paper web and the removal of moisture from it. During drying process, the temperature of the paper can reach up to 120 ºС, and humidity at the output - up to 5% [2].
The entire drying process consists of three periods: 1) warming the paper web, 2) main drying, 3) final drying. Each of these stages is characterized by its features of heat and mass transfer and various tasks in terms of control.
The warming process is the first stage of drying the paper web.
Its task is to bring the temperature of the paper web to the work value, the temperature at which the effective removal of moisture begins. The dynamics of this process impact the effectiveness of further drying and most of the parameters of quality [3].
During the second period, it is necessary to allocate the maximum amount of moisture from the paper web. In the period of drying - to align the temperature and moisture field of the paper web.
-
II. Statement of the Problem
Paper web is a capillary-porous colloidal material. As a result of the high temperature, it comes up with considerable jump-free increasing, there are irreversible processes of changing its internal structure, the destruction of paper filters, which aggravate the physicalmechanical indices of finished products, namely, discontinuous length, density, strength on breakage during multiple bends, resistance to dampening.
In this regard, it is necessary to smoothly change the temperature of the paper on each drying cylinder and prevent it from overheating.
During the process of controlling heating the paper web, it is necessary to have data about the optimum temperature values of the paper at the output of each drying cylinder and at the end of free movement areas.
Such information will provide an opportunity to analyse the quality of the process and form control impacts that ensure the production of a paper web with the necessary indicators of mechanical strength and increasing the resource and energy efficiency.
-
III. The Criterion for Controlling the Process of Heating the Paper Web.
Based on the results of previous studies [4], analysis of solutions in aspects of reliability and quality control of industrial processes [5,6,7,8], a criterion for controlling the process of heating the paper web has been proposed and the limitations on the temperature change of the paper on the drying cylinders and free movement areas have been formed in accordance with the change in the parameters of the quality of the finished product and the critical values which is specified in the standard [9].
The criterion for optimal control of the process of heating the paper web is as follows:
п
1(т™й) = ^jjpal - Tlzad)2 ^ min
1=0
where T ireal - is the actual temperature of the paper at the end of the i-th-interval, °С; T izad - is the task at the temperature of the paper at the end of the i-th interval, °С;
The number of intervals depends on the type of paper that is manufactured and the type of PM (number of drying cylinders may vary from 4 to 15), and restrictions:
। j-reaZ
-
т™41 —e
F c л m
'c ■ < FC < F£ , mm — 1 i — 1 max
Tc. < Tc < Tc 1 mm — 11 — Lm max
.Restrictions on quality parameters, where e - permissible temperature deviation (depends on the type of paper), ° C;
F ic – vapor flow in the pipeline to the drying cylinder on the i-th interval, kg / h;
F minc , F maxc – the allowable maximum values of steam flow in the pipeline to the drying cylinder, kg / h;
Tmin c - the minimum temperature value at which the paper quality parameters correspond to the values set in the standard, °С;
Tmax c - the maximum temperature value at which the paper quality parameters correspond to the values set in the standard, ° С.
Limitations on quality parameters depend on the type of paper being produced and formed separately.
Limit values of quality parameters are standardized for each type of paper. In general, the following parameters are standardized:
-
1. Weight of 1 m2 of paper, g.
-
2. Thickness г / см2.
-
3. Discontinuous length, м.
-
4. Breakdown strength during multiple bends,
-
5. Degree of gluing, mm.
-
6. Whiteness of each side,%.
-
7. Smooth.
-
8. Mass fraction of ash,%.
-
9. Linear deformation,%.
-
10. Bursting, number of rubbish per 1 m2.
-
11. Moisture, %.
-
12. Surface stability to plucking, м/с.
amount of double bends.
Restrictions were imposed for all of these quality parameters. Restrictions for «discontinuous length» is as follows :
Rd(i)≥Rd gost(s)
where Rdgost ( s ) – parameter value for «discontinuous length» is given in the standard (this value is determined by the types of paper); s – the definition of the final product (Higher, First, A, B).
In the expression Rd(i)≥Rd gost(s) it is necessary to understand that i referring to the interval at the range 1…n. In that case, Rd(i) – parameter value of «discontinuous length» for the paper web at the end of the 1-th interval.
Durability at breakage during multiple bends (double bends):
Dd(i)≥Dd gost(s)
where Ddgost ( s ) –the number of double bends is given in the standard ( this value is different for different types of paper).
Gluing degree:
Sp(i)≥Sp gost(s)
where Spgost ( s ) – the value of the "gluing-up" parameter. It is given in the standard (this value is determined by the types of paper). This parameter is unique for all types of paper (which is considered as an example) and therefore the coefficient "s" is absent.
Paper weight:
Mgost(s)min≤M(i)≤Mgost(s)max where Mgost(s)min , Mgost(s)max – the minimum and maximum legitimate mass values of 1 m2 are given in the standard (this value is different for various types of paper).
The humidity value in the process of heating part does not impose a limitation due to the small amount of water removed from the material. This feature is due to the low temperature of the paper at this drying period.
Dependence between the qualitative parameters and the drying cylinder temperature is established as follows:
qualitative parameter = f (drying cylinder temperature).
For the parameter of “discontinuous length” we get the following dependence:
Rd=r1*T+r0 , where Rd – value of discontinuous length parameter, m; T – the drying cylinder temperature, °С; r1, r0 – weight coefficients that depends on the technological parameters of the process and the characteristics of the paper web.
For tensile strength during multiple bends a more complex dependence is formed. It is necessary to apply a piecewise-specified function for the dependence description whereas the value of this parameter is a discrete value:
Dp =
( Dp
i
,T
i
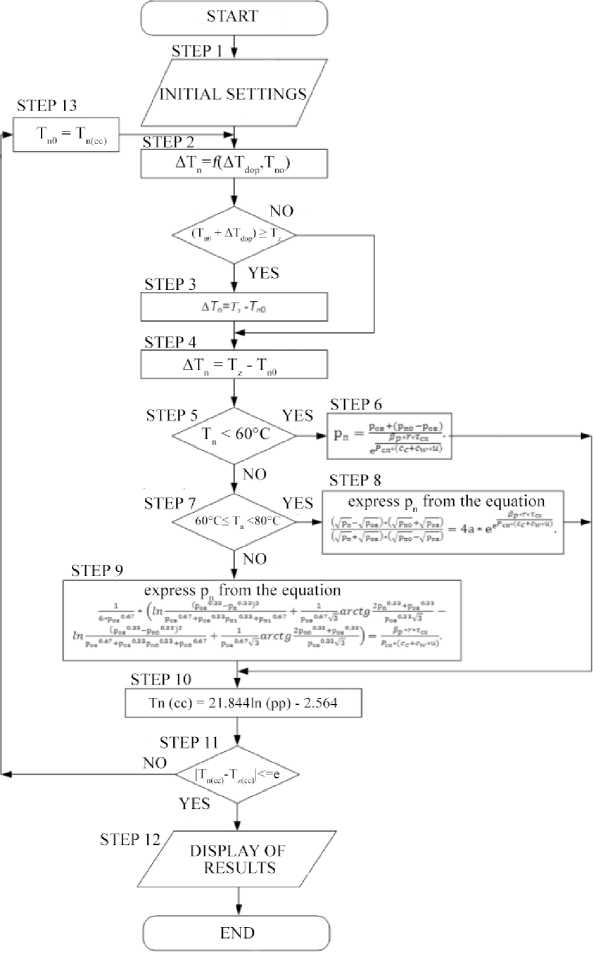
I Dp2,T2 I Dpn,Tn-1 For the gluing degree parameter: Sp=s2*T2+s1*T+s0 where Sp – degree of gluing, mm; s2, s1, s0 – weight coefficients whose values depend on technological parameters of the process and the features of paper web. IV. Optimum Graph of Heating the Paper Web To calculate the value of the proposed optimal control criterion, first of all, it is necessary to have information about the temperature issue at the end of each drying cylinder and free movement area. Moreover, in case of an extremely fast process duration and a change of large amount of technological parameters arises the problem of obtaining dynamically changing optimal temperature graph of heating a paper web by taking into account the peculiarities of the technological process. At the same time, the solving of the designated problem should take into account the necessity of speeding up the paper’s temperature to the prescribed value (completion of the warming-up). However, since the paper refers to capillary-porous colloidal substance, therefore, with a sharp increase of temperature, occurs irreversible processes of destruction of the internal structure which leads to a significant deterioration of qualitative parameters. It`s also leads to the surface contamination of the drying cylinders and dramatically reduces efficiency of drying. To sum up, it is formed the test to obtain the optimal temperature graph of heating which will provide the most rapid heating of the paper to the optimal value with restrictions on the quality indicators of the final product by taking into account rapid change of technological parameters of the process. The general view of the optimal temperature graph of heating the paper web is as follows: Tgr (P1) - the maximum permissible value of the temperature of the paper web at the end of the heating stage, limited by the most sensitive quality parameter, °C; Tgr (P1) is the minimum permissible value of the temperature of the paper web at the end of the heating stage, limited by the most sensitive quality parameter, °C; T_final - temperature of the paper at the end of the heating stage, °C; T_initial - the temperature of the paper at the beginning of the warm-up phase, ° C; Tst(min) - minimum initial possible temperature of the paper, °C; Tst(max) - maximum initial possible temperature of the paper, °C; As can be seen from the analysis of Figure 1, in each cycle, there are 2 critical points that correspond to the temperature at the end of drying cylinder and at the end of the free movement area. Consequently, to construct a temperature drying graph, it is necessary to calculate two sets of temperature values, named: at the moment of paper leaving the drying cylinder (the first critical point) and its corresponding value at the end of the free movement area (second critical point). The number of cycles (n), and hence the drying cylinders are determined by the type of paper produced and the characteristics of the PM. Fig.1. The general optimum graph of heating the paper web V. Algorithm for Calculating the Optimal Temperature Graph for Heating the Paper Web The process of calculating the optimal temperature graph of heating a paper web is advisable to submit in the form of a step-by-step algorithm. This allows its further implementation in form of special mathematical form and software for modeling the overall drying process and the creation of a system for automatic control of the drying part of the PM. The algorithm consists of 2 parts: - calculation of the temperature of the paper web on the drying cylinder; - calculation of the temperature of the paper web on the free movement area For each of the calculations there is its own test for the final temperature (Tz and Tz(cc)) for each drying cylinder and the general task for the entire process of heating the paper web. Calculation of the temperature of the paper web begins from the moment the paper arrives on the first drying cylinder. Currently available information from the following sensors: - temperature of the paper web on the press part; - humidity of the paper web on the press part; - Air temperature in the drying section of the paper machine; - Humidity of air in the drying section of the paper machine. - Data on the geometric dimensions of the drying section (drying cylinder parameters, free movement areas), as well as data on the type of paper produced, the critical values of its quality indicators, which are standardized by the relevant standard (GOST, DSTU). The result of the algorithm's operation is the array of temperature of the paper web at the end of each drying cylinder and free movement area, which corresponds to the optimum temperature graph of heating the paper web. The block diagram of the algorithm for calculating the optimal temperature graph of heating the paper web is shown in Fig. 2 The developed algorithm should be supplemented with calculation units for: 1. Pressure in the environment. 2. Pressure over the paper web surface. 3. Duration of paper stay on the free movement area. 4. Value of heating the paper on the drying cylinder, taking into account the temperature decrease on the previous free motion area. 5. Mass transfer coefficient, as a function of the partial pressure above the paper web surface and in the environment. Block 1. To start the algorithm, the initial parameters of the process, the temperature and humidity of the paper at the entrance to the drying cylinder, the parameters of the drying cylinder and the environment in the free movement region are introduced. Block 2. Calculation of the heating value of paper on the drying cylinder (depending on the initial temperature Тn0 and the allowable value of temperature change ΔTdop, quality restriction). Block 3. If the temperature at the exit from the current drying cylinder exceeds the task temperature (Tn0 + ΔTdop) ≥ Tz, it is necessary to reduce the value of ΔTdop, otherwise, it will cause overheating of the web and decrease of qualitative indicators, and then proceed to block 4. If (Tn0 + ΔTdop) Block 4. Calculate the permissible change in the temperature of the paper web on the current drying cylinder (without overheating): ΔTn = Tz - Tn0. It will then go to block 5. Block 5. Based on the temperature at the beginning of the drying cylinder Tn0 and the heating value ΔTn, we calculate the temperature at the end of the current cylinder: Tn = Tn0 + ΔTn Fig.2. Algorithm for calculating the optimal temperature graph of the heating of a paper web. After its exit from the drying cylinder, the paper passes through the area of free movement. The temperature web at the output is calculated according to the formula proposed in [10]: Tn (cc) = 21.844ln (pn) - 2.564, where pn – the partial pressure on the material surface, Pa. This value depends on the temperature of the paper at the beginning of the free motion (the exit from the drying cylinder). The calculation of pn should be carried out according to different formulas, depending on the temperature value. Block 6. If Tn <60 °C, it will then calculate pn and go to block 7. Otherwise, go to block 8. Block 7. The calculation of pn is carried out according to the formula proposed in [10]: _ pov + (pn0 - pov) P” = errT ~ eP cn (cc+cwu) where pn, pov – the partial pressures on the surface of the material and in the environment, Pa; βr – the mass exchange coefficient, it is assigned to the difference of partial pressures, kg / (m2 * h * Pa); where pn, pov - partial vice on the surface of the material and in the environment, Pa; cc - heat capacity of dry material, kJ/(kg°C); cw - heat capacity of water, kJ/(kg°C); τ - time of the paper in the area of free movement, c; Pcn - mass of square meter of dry web, g/m2; u - the moisture content of the paper web, kg/kg. After that we go to block 11 to calculate the final temperature. Block 8. If 60 °C≤ Tn <80 °C, it will go to block 9. If the temperature exceeds 80 °C, it will go to block 10. Block 9. pn calculation based on a formula is proposed in [10]: №zVPOV)№0.±VPOV) (√рn + √рov)(√рn0 - √рov) βrrτ еPcn(cc+cwu) After that we go to block 11. Block 10. At the temperature of the paper, the exit from the drying cylinder is more than 80 °C, the calculation of pn should be carried out by the iteration method [11] from the previous equation, as indicated in [10]: (рov0,33 - рn0,33)2 1 6рov0,67 (lnрov0,67 + + рov0,33рn10,33 + рn10,67 1 2рn0,33 + рov0,33 arctg Л С.П Гп Л ОО Гп рov 0,33 рov рn00,33)2 0,33 (рov - ln рov 0,67 + рov0,33рn00,33 + рn00,67 + рov0,67√3 βrrτ 2рn00,33 + рov0,33 arctg рov0,33√3 Pcn (cc + cwu) Block 11. According to the value pn (depending on the initial temperature) calculate the temperature in the end of free movement area. Block 12. If: |Tn(cc) - Tz(cc)| < е where e is the allowable maximum temperature deviation at the end of the free motion region, the heating process is complete and the system produces a temperature graph (optimal values of the temperature of the paper on each drying cylinder and the free movement area) [12]. If equality is not satisfied, the heating process should be continued on the next drying cylinder. Block 13. The temperature at the input of the next drying cylinder is assigned to a temperature value at the end of the free movement area and the algorithm begins from the beginning. VI. Conclusion This paper proposed a solution for calculating the optimal temperature graph of heating a paper web in the drying section of the paper machine. The main attention during the development of this solution is given by considering the peculiarities of the processes of heat and mass transfer at different temperatures of the paper and the drying cylinder, taking into account the partial pressures on the surface of the paper web and in the environment. The result of the work is presented in the form of the stepwise algorithm implemented in form of special software for calculating and adjusting the optimal temperature graph of the heating of the paper web in real time. The developed algorithm includes the following main elements: • Initialization of initial parameters; • Calculation of the optimal amount of paper heat on each drying cylinder; • Calculation of the value dropping in the temperature of the contact layer of the paper web on the free movement areas; • The choice of formulas for further calculation based on information on the current value of the temperature of the paper web; • Checking the optimum value of the temperature web or transferring the calculation to the next drying cylinder. • The main advantages of the proposed algorithm are: • Versatility for different types of paper and drying parameters; • Ease of implementation in different programming languages and in various software environments. The use of the proposed algorithm provides an opportunity to improve the quality control of heating the paper web and the entire drying process as a whole. Results of the work were tested on the "Kyiv Cardboard and Paper Mill" Obukhiv, Kyiv region. Further development of work will be carried out in two directions: a) Development of a new system for controlling heating the paper web based on the proposed algorithm. b) Development of this algorithm for calculating the optimal temperature graph of the entire drying process with the development of a comprehensive control system.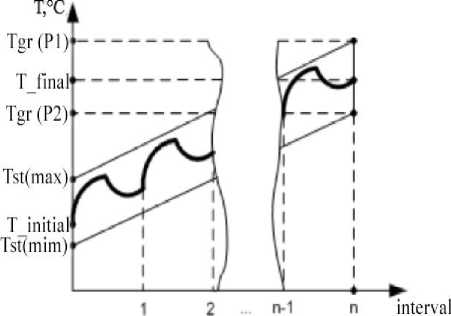
Список литературы Formation of optimum temperature graph of paper web warming
- Pulp and paper capacities. Food and agriculture organization of the united nations. Rome, Roma, 2016.
- Ivanov S. N. Tehnologiya bumagi. – M.: Lesn. prom-st, 1970. – 696 s. (in Russian)
- Karlsson, M. Papermaking Science and Technology: Papermaking Part 2, Drying, (ed), Finnish Engineers’ Association and Tappi, Chapter 9 (2000). – P. 81-86.
- Cheropkin E. S. Postanovka zadachi optimalnogo upravleniya protsessom progreva bumazhnogo polotna v sushilnoy chasti bumagodelatelnoy mashinyi. / Zhuchenko A. I., Cheropkin E. S. // Avtomatizatsiya promislovih i biznes protsesiv. – O.: 2015 – # 22. – S. 25-31. (in Russian)
- Zhao Xiuxu, Zhu Yuming, "Application Research of Ontology-enabled Process FMEA Knowledge Management Method", International Journal of Intelligent Systems and Applications(IJISA), vol. 4, no. 3, pp. 34-40, 2012. DOI: 10.5815/ijisa. 2012.03.05
- Saeid A. Keshtgar, Bahman B. Arasteh,"Enhancing Software Reliability against Soft-Error using Minimum Redundancy on Critical Data", International Journal of Computer Network and Information Security(IJCNIS), Vol.9, No.5, pp.21-30, 2017.DOI: 10.5815/ijcnis.2017.05.03
- Darakshan Anjum, Tasleem Mustafa,"Reliability of Software Correlated Components Failure in Pakistan Industry", International Journal of Information Engineering and Electronic Business (IJIEEB), Vol.9, No.2, pp.27-35, 2017. DOI: 10.5815/ijieeb.2017.02.04
- Michael Onuoha Thomas, Babak Bashari Rad,"Reliability Evaluation Metrics for Internet of Things, Car Tracking System: A Review", International Journal of Information Technology and Computer Science (IJITCS), Vol.9, No.2, pp.1-10, 2017. DOI: 10.5815/ijitcs.2017.02.01
- Belskiy A. P. Spetsialnyie voprosyi teplomassoobmena v energeticheskih i teplotehnologicheskih protsessah i ustanovkah: uchebnoe posobie. – Izd. 2-e, ispr. i dop. / A.P. Belskiy, V.Yu. Lakomkin– GOUVPO SPb GTU RP. – SPb.: – 2011. – 98 s.: il. 38. (in Russian)
- Lakomkin V. Yu. Teplotehnicheskiy raschet mnogotsilindrovoy sushilnoy chasti bumagodelatelnoy mashinyi: metodicheskie ukazaniya / V. Yu. Lakomkin, A. P. Belskiy – GOUVPO SPb GTU RP. – SPb.:– 2006. – 230 s. (in Russian)
- Kubrak A. I. Chislovi metodi. Algoritmi i programi: [navch. posib.] / Kubrak A. I., Zhuchenko A. I., SitnIkov O. V.; Nats. tehn. un-t Ukraini "Kyiv. politehn. in-t". – K.: Poltehnika, 2013. – 389 s. (in Ukrainian)
- Lyikov A. V. Teoriya teploprovodnosti. Uchebnoe posobie. – M.: Vyisshaya shkola, 1967. – 600 s. (in Russian)


