Формирование двумерных панорамных радиолокационных изображений объектов с помощью измерительного комплекса открытого типа

Наряду с традиционными задачами радиолокационного наблюдения (обнаружение и разрешение объектов, измерение их параметров движения и координат) в настоящее время особое внимание уделяется решению задачи распознавания объектов радиолокационными средствами.

Одним из методов решения задачи распознавания объектов является формирование и анализ их радиолокационных изображений (РЛИ), которые рассматриваются в качестве сигнального признака распознавания [1].

Формирование двумерного РЛИ может быть осуществлено с использованием широкополосных зондирующих сигналов и метода инверсного синтезирования апертуры за счет вращения исследуемого объекта [2–5]. В последнее время в нашей стране создано несколько радиолокационных измерительных комплексов (РИК), позволяющих формировать двумерные РЛИ указанным способом в условиях открытого полигона.

Вопросу формирования двумерных РЛИ посвящено достаточное количество работ [2–7], однако, в них рассмотрено получение РЛИ тестовых объектов, состоящих из небольшого числа локальных центров рассеяния (ЛЦР). При этом используется узкий сектор синтезирования (10…25 градусов), в пределах которого отражательные характеристики ЛЦР остаются постоянными и отсутствует эффект затенения ЛЦР друг другом.

Очевидно, что ЛЦР, расположенные на поверхности реальных объектов сложной формы, особенно крупногабаритных, имеющих максимальный линейный размер 10 м и более, не удовлетворяют приведенным выше условиям, что обуславливает необходимость доработки алгоритмов формирования двумерных РЛИ.

На основе анализа значительного количества РЛИ реальных крупногабаритных объектов сложной формы, полученных для узких секторов синтезирования (частных РЛИ), было установлено, что улучшение качества распознавания и более точная оценка их пространственноэнергетических характеристик, могут быть достигнуты при построении панорамного РЛИ. Под панорамным РЛИ понимается радиолокационное изображение, сформированное в результате совместной обработки совокупности частных РЛИ, полученных в узких секторах синтезирования для различных углов наблюдения.

Цель работы – изложить способ формирования двумерных панорамных РЛИ с использованием РИК открытого типа.

В основе получения двумерных РЛИ реальных объектов с использованием РИК открытого типа лежит известный [2; 3] способ формирования РЛИ путем преобразования Фурье комплексных огибающих отраженных сигналов, измеренных при многочастотном импульсном зондировании и инверсном синтезировании апертуры и представленных в координатах пространственных частот.

Из математических соотношений [3; 5], с учетом технических характеристик РИК, определим

Рис. 1

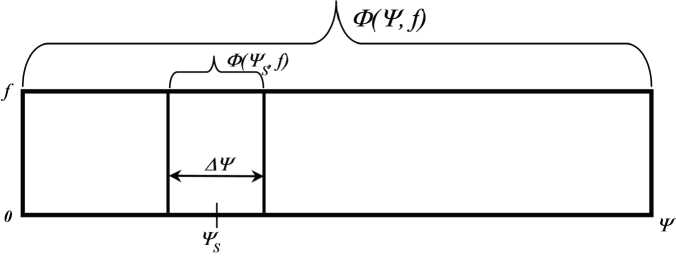
величину оптимального сектора синтезирования А^, обеспечивающего наилучшую одинаковую разрешающую способность двумерных РЛИ по продольной А z и поперечной А x координатам, в

трицы с индексами z и x заносятся значения n_z и m_x , вычисленные по формулам:

^fztek ² + f xtek ²- f min

соответствии с выражением:

nz

Аf

;

А^ =

A

Г

= 2Arctg -0,4 ±

V

0,2

Г 2 fcp +А F f

2 fen — А F V ^ср у

- 0,04

где А F — диапазон перестройки дискретно-частотного сигнала РИК; f_ср – средняя частота диапазона перестройки А F .

Линейные размеры площади синтезирования по продольной – L_z и поперечной – L_x координатам должны быть больше максимального линейного размера исследуемого объекта l _max и удовлетворять условию L_z = L x .

Для выполнения нелинейного преобразования комплексных огибающих отраженных сигналов Ф(% f ), измеренных в координатах ¥ и f , в координаты пространственных частот f_z и f_x , создадим двумерную матрицу преобразования координат (матрицу индексов) T_{Nz , Mx} , и, опираясь на математические соотношения, приведенные в [3; 5], определим размерность этой матрицы ( N_z , M_x ) и размеры площади синтезирования РЛИ L z х L x по продольной z и поперечной x

координатам:

N_z = L z (max f_z - min f_z );

M = L (max f - min f ), xx x x где max fz, min fz, max fx, min fx – максимальные и минимальные значения пространственных частот по продольной и поперечной координатам.

При этом для увеличения скорости работы БПФ целесообразно обеспечение выполнения условия N_z = M x = 2 n .

Формирование матрицы индексов | T_{Nz , Mx} | проводится следующим образом: в элементы ма-

mx

B

V VP

где f_ztek

= min f + — z L_z

- +1 , У и fxtek = min fx

x

⁺ Lx^: B "

количество проходов

по всему частотному диа-

пазону в секторе синтезирования А^; f min — ми

нимальная частота диапазона; А f = А F / ( H - 1) —

шаг перестройки частоты; H – количество дискретных частот диапазона перестройки А F ; z = 0,1, 2,..., N_z ; x = 0,1, 2,..., M_x .

Отметим, что в отличие от способа формирования матрицы индексов, предложенного в [3], в рассматриваемом способе отсутствует третий

вложенный цикл определения значений n_z и m_x , что существенно увеличивает скорость форми-

рования матрицы индексов.

Зададим произвольный угол наблюдения ¥ _s , который определяет середину сектора синтезирования А^. Из исходного массива Ф(^, f ) комплексных огибающих сигналов, отраженных от объекта, сформируем частный массив комплексных огибающих Ф(^ _s , f ) для сектора синтезирования ^ _s ± А^ / 2, порядок формирования которого представлен на рис. 1.

Далее создадим матрицу | Ф _{Nz Mx} | _s комплексных огибающих сигналов, отраженных от объекта, в координатах пространственных частот. Заполнение матрицы выполняется следующим образом: в элементы матрицы |Ф _{Nz Mx} | _s с индексами z и x заносятся значения из ячеек массива Ф(^ _s , f ), индексы элементов которого определены в матрице индексов | T_{Nz , Mx} | в ячейках с индексами z и x .

В комплексных значениях элементов матрицы | Ф Nz _Mx | _s выполним корректировку ампли-

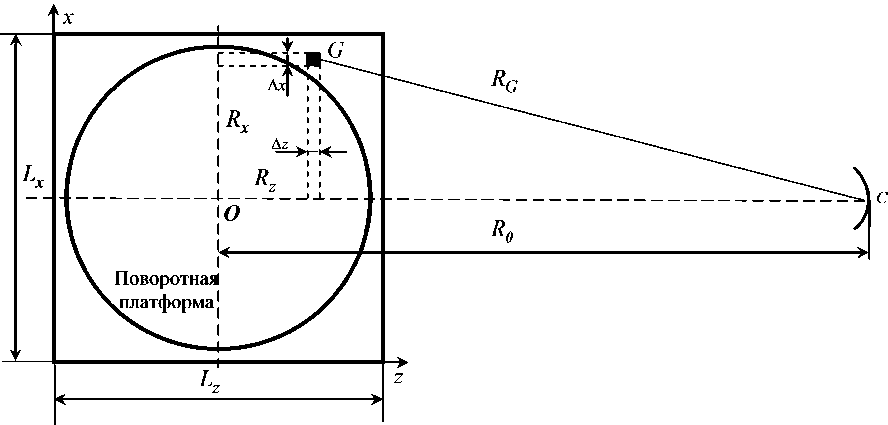
Рис. 2

туды и фазы с учетом разности расстояний до элементов синтезирования. Пояснение к определению расстояний приведено на рис. 2. Здесь G — произвольный элемент синтезирования, A z и A x — его линейные размеры, а R_z и R_x — его координаты на площади синтезирования относительно центра вращения O .

В соответствии с [5], опорная функция имеет вид:

• о    . 4 nA R

• ² - j

R G I „ ^X ср

• e ,

Ro J                ________________ где AR = Rg - Ro; Rg = ^(Ro + Rz )2 + Rx2, Rz = = Lz (z/Nz - 0,5), Rx = Lx (x/Mx - 0,5); Ro — расстояние между фазовым центром С антенны

РИК и центром площади синтезирования О ; R_G – расстояние между фазовым центром С антенны РИК и элементом синтезирования.

Таким образом, для выполнения корректировки необходимо амплитуду каждого комплексного значения матрицы | Ф n_z m_x | _s умножить на коэффициент K a = ( Rg / R o ) ² , а значения фазы увеличить на Аф = 4п A R / X _ср , где X _ср — средняя длина волны многочастотного РИК.

Для снижения уровня боковых лепестков от синтезируемых откликов выполним фильтрацию матрицы | Ф Nz m_x | _s окном Хемминга.

Скорректированную и отфильтрованную двумерную матрицу | Ф Nz Mx |s комплексных огибающих сигналов, отраженных от объекта, для выбранного сектора синтезирования ^s ± A^ / 2 подвергаем двумерному быстрому дискретному обратному преобразованию Фурье, в результа- те которого получаем матрицу синтезированных откликов двумерного РЛИ | DNz,Mx |s в координа- тах площади синтезирования и объекта. По полученной двумерной матрице синтезированных откликов двумерного РЛИ объекта | DNz,Mx |s построим изображение, которое будет частным РЛИ для выбранного угла наблюдения ^s.

В качестве примера на рис. 3 приведены двумерные частные РЛИ крупногабаритного объекта сложной формы типа «транспортная база» для углов наблюдения 330° — рис. 3, а и 0° — рис. 3, б .

Данные РЛИ получены при размещении объекта на поворотной платформе и его вращении в горизонтальной плоскости с постоянной угловой скоростью 0,5 град/с. Зондирование объекта осуществлялось дискретно-частотным импульсным сигналом в полосе перестройки частоты 8,464…11,530 ГГц с постоянным шагом 6 МГц, длительностью импульсов 0,35 мкс и периодом следования 50 мкс. При построении изображений выполнена обработка сигнала весовым окном Хемминга с соответствующей нормировкой амплитуды.

Формирование РЛИ выполнено в связанной с объектом декартовой системе координат, начало отсчета которой совпадает с осью вращения поворотной платформы. Диапазон изменения уровней откликов, полученных от ЛЦР различной мощности, показан на РЛИ в градациях серого цвета.

Из анализа изображений видно, что они позволяют, в пределах выбранного угла наблюдения, определить количество ЛЦР объекта сложной формы и их координаты с привязкой к выбранной системе отсчета. Кроме того, имеется возможность определения по РЛИ доминирую-

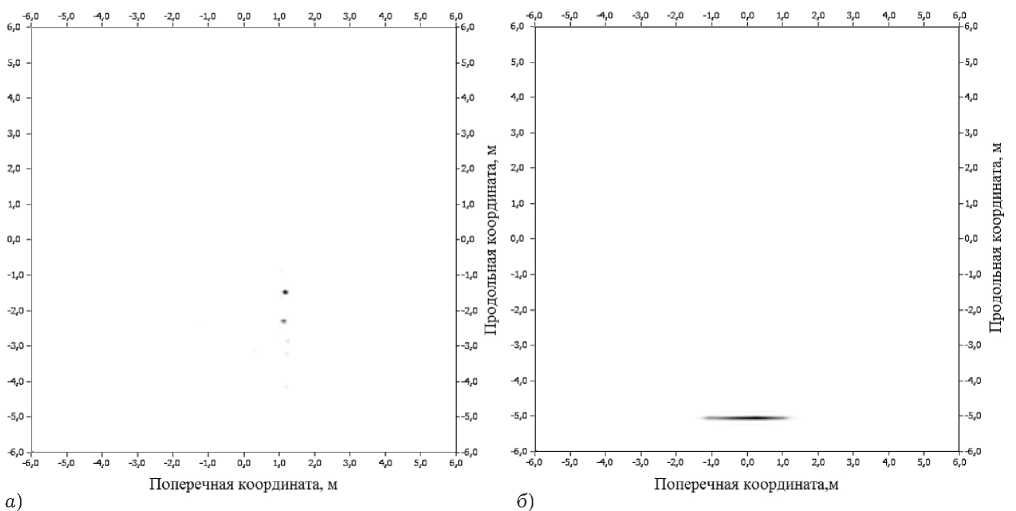
Рис. 3

щих ЛЦР и оценки их отраженной мощности, выраженной в дБ. Вместе с тем следует отметить, что по результатам анализа отдельных частных РЛИ, в большинстве случаев, достаточно затруднительно получить представление об объекте сложной формы в целом и таким образом провести его правильную идентификацию.

Перейдем к получению и анализу панорамного РЛИ [8]. Как уже было отмечено выше, оно представляет результат совместной обработки совокупности частных РЛИ.

В качестве условий формирования панорамного РЛИ определим суммарный сектор синтезирования Т, начальное значение и дискретность изменения угла наблюдения Т _s .

Величина суммарного сектора синтезирования Т может изменяться от значения сектора синтезирования АТ (для частного РЛИ) до 360° (в случае формирования РЛИ объектов, наблюдаемых вкруговую).

За начальное положение угла наблюдения, для удобства, примем нулевое значение — T q = 0°, тогда следующие положения угла наблюдения могут быть определены в соответствии с выражением

Т s = 5 • s, где 5 — дискрет изменения угла наблюдения, определяемый исходя из требуемого качества изображения и времени его получения. Опытным путем установлено оптимальное значение 5 в интервале 1° ^ 5°; s = 0,1, 2, ..., smax - номер текущего положения угла наблюдения Тs, мак- симальное значение которого определяется по формулам:

Г 360°            _ smax =   . , если Т = 360 , sma„ =-------, если Т < 360°.

max

• I              5

Для начального положения T q получим, в соответствии с рассмотренным выше алгоритмом, частное РЛИ в виде матрицы | D_{Nz , Mx} |₀ синтезированных откликов двумерного РЛИ.

Далее зададим следующее положение s = 1 угла наблюдения Т =5 и сформируем, после обработки частного массива данных Ф(Т_Ь f ), матрицу | D_{Nz , Mx} |₁ синтезированных откликов двумерного РЛИ. На рис. 4 показан порядок формирования частных массивов данных Ф(Т _s , f ) для углов наблюдения Т _s со сдвигом 5 из исходного массива Ф(Т, f ).

Координаты ( z ₁, x ₁) синтезированных откликов двумерного РЛИ с угла наблюдения Т приведем к системе координат объекта путем их поворота на угол минус Т₁ в соответствии с алгоритмом, предложенным в [9] при s = 1:

z = z„ cos Т, + x„ sin Т,; s ss s x = -zs sin Тs + xs cos Тs.

Изменим значение ячеек матрицы синтезированных откликов двумерного РЛИ | D_{Nz , Mx} |₀ следующим образом: выбираем большее значение из ячеек с одинаковыми индексами z и x матриц | D_{Nz , Mx} |₀ и | D_{Nz , Mx} |₁ и заносим его в матрицу | D_{Nz , Mx} |₀, которую после выполнения

Рис. 4

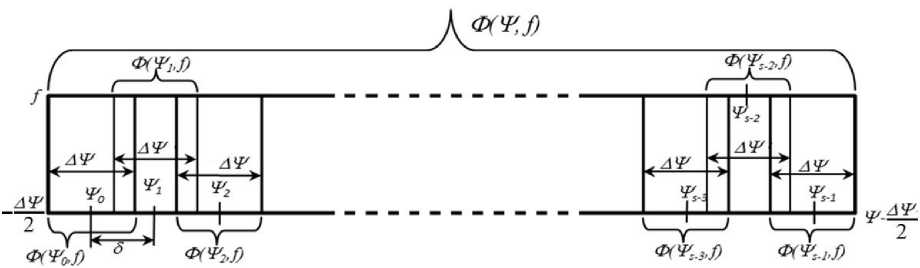
Рис. 5

[р о дольная коорди]

Рис. 6

описанной процедуры назовем результирующей матрицей. Выполним построение изображения по данным результирующей матрицы синтезированных откликов | D_{Nz , Mx} |₀, но уже для двух положений угла наблюдения (Ψ₀ и Ψ₁). При этом суммарный сектор синтезирования будет равен ∆Ψ + δ.

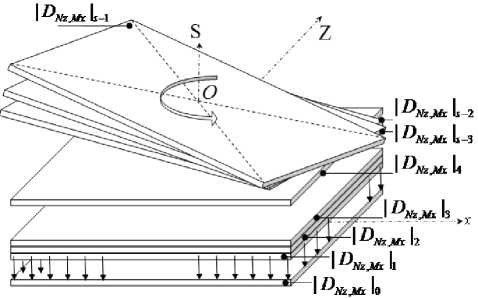
Последовательно изменяя положение угла наблюдения Ψs с шагом δ и выполняя действия, описанные выше, получаем панорамное РЛИ объекта во всем секторе синтезирования Ψ. На рис. 5 приведена последовательность формирования результирующей матрицы DNz,Mx двумерного панорамного РЛИ.

На рис. 6 представлено двумерное панорамное РЛИ ( а ) и габаритный чертеж ( б ) объекта типа «транспортная база».

Таким образом, изложенный способ формирования двумерных панорамных РЛИ позволяет получать РЛИ реальных объектов сложной фор- мы, в том числе крупногабаритных, с применением радиолокационных измерительных комплексов открытого типа и обеспечивает практическое решение задачи распознавания объектов. Данный способ может быть взят за основу при разработке алгоритма получения трехмерных объемных РЛИ объектов.

Ñïèñîê ëèòåðàòóðû

• 1.    Радиолокационное распознавание и методы математического моделирования / С.А. Горшков [и др.]; под ред. Я.Д. Ширмана. Выпуск III. Радиолокация и радиометрия. М.: Радиотехника, 2000. С. 5–65.

• 2.    Патент RU 2372627. Способ получения двумерного радиолокационного изображения объекта в большом диапазоне величин эффективных площадей рассеивания локальных центров при многочастотном импульсном зондировании / Блиновский А. М., Крюков С.В.

• 3.    Патент RU 2422851. Способ получения двумерного радиолокационного изображения объекта при многочастотном импульсном зондировании / Ковалев С.В., Нестеров С.М., Скородумов И.А.

• 4.    Формирование радиолокационных изображений объектов при многочастотном импульсном зондировании и инверсном синтезировании апертуры / С.В. Ковалев [и др.] // Радиотехника. 2007. № 6. С. 80-84.

• 5.    Методы исследования радиолокационных характеристик объектов / В.С. Бачурин [и др.]; под ред. С.В. Ягольникова. М.: Радиотехника, 2012. 289 с.

• 6.    Беляев В.В., Кирьянов О.Е., Понькин В.А. Радиолокационные, антенные и радиофизические измерения. Воронеж: Издательско-полиграфический центр «Научная книга», 2013. 319 с.

• 7.    Штагер Е.А. Рассеяние радиоволн на телах сложной формы. М.: Радио и связь, 1986. 184 с.

• 8.    Патент RU 2629372. Способ построения панорамного радиолокационного изображения объекта / М.Е. Замарин [и др.].

• 9.    Поворот изображения на произвольный угол [электронный ресурс]. URL: http://zhukovsd.blogspot.ru/2010/04/ blog-post.html (дата обращения 08.14.2014).

The formation of two-dimensional panoramic radar images of objects using an open-type measuring complex

V.P. Aterley, D.L. Dobrynin, V.N. Myazin, G.A. Schevchenko