Формирование фотонных наноструй двумерными микропризмами

Преодоление дифракционного предела, или острая фокусировка света, является актуальной задачей в современной оптике и нанофотонике [1 –6]. Острая фокусировка находит свое применение в таких областях, как оптические системы памяти [7], рамановская спектроскопия [8], наноструктурирование [9], оптическое манипулирование [10] и нанолитография [11, 12].

Интересно, что для получения острого фокуса бывает достаточно использования простых объектов микрооптики, например, диэлектрических цилиндров, отдельных диэлектрических ступенек, микросфер, формирующих вблизи своей поверхности области повышенной интенсивности – фотонные наноструи [13– 19]. Основной целью работы обычно является достижение сверхмалых поперечных размеров фокуса. В [13] с использованием метода конечных разностей во временной области (метод FDTD) показано наличие фотонных наноструй с шириной по полуспаду интенсивности FWHM = 0,72 λ при распространении света через отверстие микротора. Длина фотонной наноструи составляла 37 λ. В [14] авторы получи- ли сверхдлинный фокус (28 λ) с шириной по полуспаду интенсивности менее 0,5 λ. Он был сформирован двухслойной диэлектрической микросферой. В [16] с использованием метода FDTD показана генерация фотонных наноструй с шириной по полуспаду интенсивности FWHM = 305 нм (0,56 λ) и FWHM = 218 нм (0,4 λ), образованных, соответственно, цилиндром и половиной цилиндра с диаметрами 5 мкм и показателем преломления n = 1,7 и освещаемых светом с длиной волны 0,55 мкм. Одним из подходов для генерации фотонных наноструй является возбуждение резонансных мод шепчущей галереи [20, 21]. В [20], используя теорию Ми и генетический алгоритм, авторы предложили пятислойный микроцилиндр, фокусирующий TM-поляризованный луч с длиной волны 0,633 мкм в ультрадлинную (107,5 длин волн) фотонную нанострую с FWHM = 0,22 λ. Для моделирования фокусировки с помощью разработанного элемента использовался метод конечных элементов (FEM), реализованный в программном обеспечении COMSOL Multiphysics. Образование фотонных наноструй с использованием материалов с показателем преломления меньше двух рассмотрено в [22]. Используя FEM, было показано, что фотонные наноструи с FWHM = 0,287 λ могут быть получены с использованием диэлектрических микрочастиц с параболической формой поверхности и показателем преломления 2,5. Фокус формируется на расстоянии, превышающем длину затухания поверхностных волн. В [23] авторы рассматривают генерацию фотонных наноструй с использованием микроцилиндров и микросфер с брэгговскими решетками. Используя теорию Ми, при фокусировке лазерного света с длиной волны 0,5 мкм авторы показали наличие узкого фокуса с FWHM = 0,117 мкм (0,24 λ). В [24] диэлектрические микросферы с радиусом 60 мкм применялись для получения массива фокусных пятен в инфракрасном диапазоне для длин волн от 3 до 5 мкм. В большинстве работ получение фотонных наноструй производится с помощью объектов сферической формы – цилиндров, сфер [13 – 24], однако подобный эффект наблюдается и при прохождении света через несферические объекты – освещаемые со стороны основания конические, бинарные и вихревые аксиконы [25– 31], микрокубики [32, 33], прямоугольные ступеньки [34], призмы [35], цилиндры, освещаемые со стороны основания [36], объекты произвольной формы [2, 37]. Например, в работе [25] была показана возможность формирования фотонной струи с шириной FWHM = 0,30 λ с помощью конического аксикона, а в работе [38] методом FDTD была рассмотрена фокусировка света многослойным диэлектрическим микрокубом. Было показано, что микрокуб с размером 4×4×4 мкм и n =2 образует нанострую с FWHM = 0,232 мкм (0,39 λ) при фокусировке лазерного импульса с длиной волны 0,6 мкм.

В данной работе рассмотрена фокусировка излучения с помощью диэлектрической треугольной призмы. Моделирование фокусировки проводилось с помощью метода конечных элементов, реализованного в программном пакете COMSOL Multiphysics. В качестве фокусируемого излучения использовался TE-поляризованный Гауссов пучок с шириной перетяжки 80 мкм и длиной волны λ =4 мкм. Было проведено исследование характеристик фокусного пятна, таких как максимальная интенсивность и ширина пятна по полуспаду интенсивности (FWHM), в зависимости от высоты и материала треугольной призмы.

Было показано, что двумерные треугольные призмы позволяют фокусировать свет в свободном пространстве в пятна с размерами меньше скалярного дифракционного предела. В частности, призма из кварцевого стекла с шириной основания 60 мкм и высотой 28,5 мкм формирует фотонную нанострую с максимальной интенсивностью, в 6 раз превышающей интенсивность падающего излучения, и шириной FWHM = 0,38 λ. А призма из титаната бария с шириной основания 60 мкм и высотой 20 мкм позволяет получить фотонную нанострую с такой же шириной (0,38 λ) и максимальной интенсивностью, в 5 раз пре- вышающей интенсивность падающего излучения. Размеры фокусного пятна можно уменьшать и дальше, если высота призмы подобрана таким образом, чтобы максимум интенсивности располагался внутри призмы. Так, например, призма из титаната бария с высотой 21 мкм и шириной основания 60 мкм формирует непосредственно за своей вершиной фокусное пятно с шириной FWHM = 0,25 λ. Также было проведено исследование характеристик фокусных пятен в зависимости от длины волны фокусируемого света. Было показано, что использование призмы приводит к меньшей зависимости ширины фокусного пятна от длины волны по сравнению с микроцилиндром. Например, у микроцилиндра из кварцевого стекла с диаметром 60 мкм смена длины волны освещающего света с 3 мкм до 5 мкм приводит к изменению ширины пятна на 0,09 λ, а у призмы – в среднем на 0,05 λ.

Фокусировка излучения треугольной призмой из кварцевого стекла

Рассмотрим диэлектрическую треугольную призму из кварцевого стекла ( n = 1,46) со стороной основания 60 мкм. Схема моделирования приведена на рис. 1.

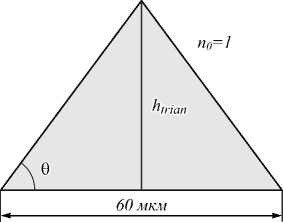
Рис. 1. Схема моделирования для треугольной призмы

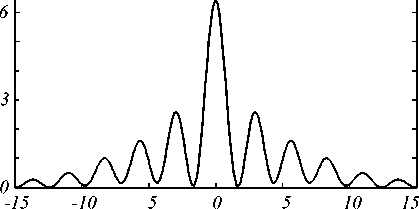
С помощью метода конечных элементов, реализованного в пакете COMSOL Multiphysics, проведем моделирование распространения TE-поляризованного излучения с длиной волны 4 мкм через рассматриваемую треугольную призму. В качестве падающей волны возьмем Гауссов пучок с шириной перетяжки 80 мкм. В ходе моделирования здесь и далее воспользуемся нерегулярными сетками с переменным шагом. Так, в областях, близких к разделу двух сред, используем сетку с мелким шагом λ /40, в то время как остальную область будем рассчитывать с шагом λ /20. На границах области располагались поглощающие слои PML. В процессе исследования будем изменять высоту треугольной призмы htrian и оценивать максимальную интенсивность Imax формируемого фо- кусного пятна и его ширину по полуспаду интенсивности FWHMx, для подбора оптимальной высоты призмы. Пример распределения интенсивности в фокусной плоскости и вдоль оси распространения света для призмы с высотой 28,2 мкм приведен на рис. 2. Результаты моделирования приведены в табл. 1 и на рис. 3.

I, отн.ед.

а)                                                         .V. Л1КМ

I, отн.ед. 8

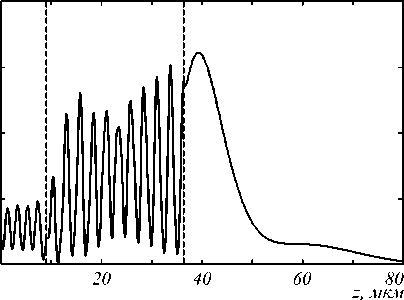
Рис. 2. Распределение интенсивности в фокусе (а) и вдоль оси распространения света (б) при прохождении ТЕ-поляризованного Гауссова пучка с шириной перетяжки 80 мкм через треугольную призму из кварцевого стекла с высотой 28,2 мкм и шириной основания 60 мкм. Границы призмы показаны пунктирной линией, z = 0 соответствует области ввода излучения в расчетную область

Из табл. 1 и рис. 3 видно, что при увеличении высоты призмы интенсивность в фокусном пятне сначала растет, достигая максимума при h = 24,3 мкм, а потом начинает уменьшаться. Ширина же фокусного пятна постоянно уменьшается и после h = 25,4 мкм становится меньше скалярного дифракционного предела (FWHM = 0,51 λ). Для призмы с высотой 28,5 мкм формируется фокусное пятно в свободном пространстве с минимальной шириной – FWHM = 0,38 λ. Если высоту увеличить до 29 мкм, то максимум полученного фокусного пятна будет располагаться внутри линзы, а непосредственно за границей раздела двух сред размер фокусного пятна составит FWHM = 0,30 λ.

Фокусировка излучения круглым цилиндром

Для оценки эффективности фокусировки света призмой было проведено исследование фокусировки круглым цилиндром из кварцевого стекла диаметром

60 мкм с помощью аналитического решения [39]. Схема моделирования представлена на рис. 4.

Табл. 1. Зависимость характеристик фокусного пятна от высоты призмы из кварцевого стекла (n =1,46)

h trian , мкм	I max , отн.ед.	FWHMx, λ	f , мкм	DOF, λ
22,6	8,20	0,60	15,5	5,63
23,4	8,67	0,60	13,1	5,00
24,0	8,87	0,58	11,9	4,63
24,3	9,01	0,50	11,2	4,38
24,5	9,00	0,55	10,4	4,25
25,4	8,65	0,53	8,6	3,88
26,8	7,73	0,40	5,7	3,13
28,2	6,02	0,40	3,2	2,50
28,5	6,43	0,38	2,8	2,40
29,0	5,85	0,30	0	1,80

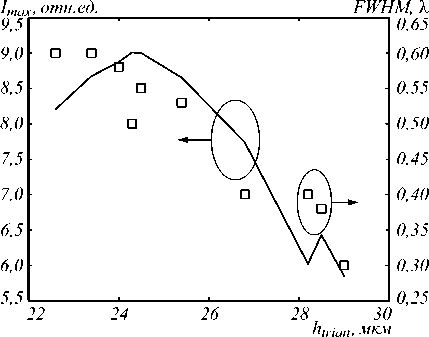
Рис. 3. Зависимость максимальной интенсивности (кривая) и ширины фокусного пятна (квадраты) от высоты призмы

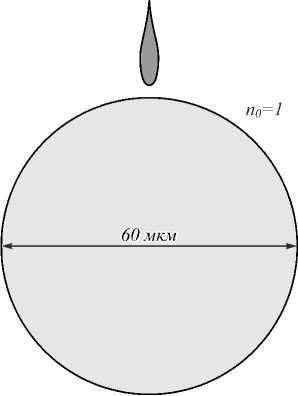
Рис. 4. Схема моделирования для круглого цилиндра

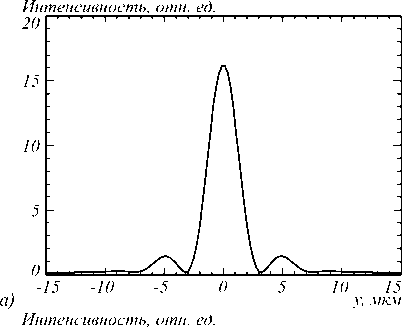
Результаты моделирования фокусировки плоской волны с длиной волны 4 мкм диэлектрическим цилиндром приведены на рис. 5.

О

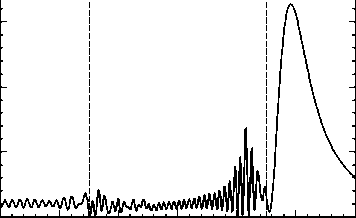
-60   -40    -20      0     20     40    60

б)                                                X, Л1КМ

Рис. 5. Распределение интенсивности в фокусе (а) и вдоль оси распространения света (б) при прохождении ТЕ-поляризованной плоской волны через круглый цилиндр из кварцевого стекла с диаметром 60 мкм

Из рис. 5 видно, что ширина фокусного пятна в данном случае равна FWHM = 0,82 λ. Сравнивая параметры фокусных пятен, полученных с помощью цилиндра круглого сечения и треугольной призмы, с одинаковыми характерными размерами, можно видеть, что призма формирует более узкое световое пятно. Однако максимальная интенсивность в фокусе призмы в 2,5 раза меньше, чем в фокусе круглого цилиндра.

На рис. 6 приведено двумерное распределение интенсивности при фокусировке Гауссова пучка на призме и круглом цилиндре.

Влияние показателя преломления на параметры фокусного пятна

Рассмотрим далее влияние показателя преломления материала призмы на характеристики формируемой фотонной наноструи. В качестве материалов для призмы в дополнение к кварцевому стеклу, рассмотренному ранее, добавим полистирол ( n 1 = 1,56) и титанат бария ( n 1 = 1,8). Результаты моделирования представлены в табл. 2, 3 и на рис. 7, 8. Фокусные пятна с наименьшими диаметрами в таблицах отмечены серым цветом.

z, мкл!                        1, отн.ед.

б

а)

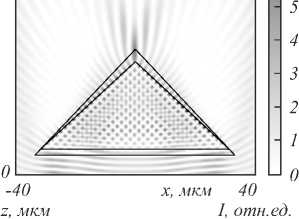
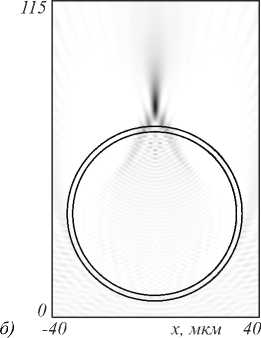
Рис. 6. Двумерная картина дифракции на призме (высота – 28,2 мкм, ширина основания – 60 мкм) (а) и круглом цилиндре (диаметр – 60 мкм) (б)

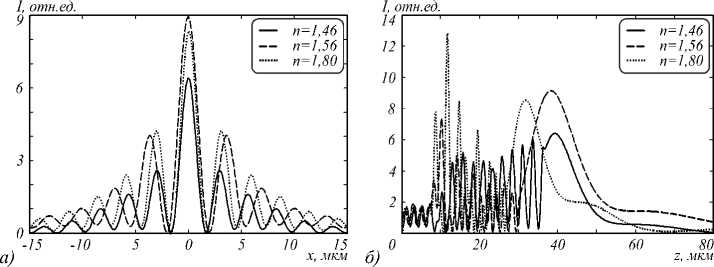
Рис. 7. Распределение интенсивности в фокальной плоскости (a) и вдоль оси распространения пучка (б) при фокусировке света диэлектрической треугольной призмой из кварцевого стекла (n = 1,46, h = 28,5 мкм, непрерывная кривая), из полистирола (n = 1,56, h = 22,6 мкм, пунктирная кривая) и титаната бария (n = 1,8, h = 19 мкм, точечная кривая)

Табл. 2. Параметры фокусного пятна для призмы из полистирола (n = 1,56)

h trian , мкм	I max , отн.ед.	FWHMx, λ	f , мкм	DOF, λ
17,54	7,66	0,70	23,7	8,25
20,04	8,04	0,60	14,8	5,25
21,29	8,37	0,55	10,5	4,13
21,79	8,70	0,50	9,25	3,75
22,04	8,77	0,50	8,80	2,38
22,55	8,85	0,47	7,93	3,38
25,05	5,84	0,40	2,79	2,25
25,30	5,86	0,38	2,41	2,08
25,55	5,75	0,38	1,90	1,88
25,80	5,26	0,30	0	1,63
26,03	4,82	0,30	0	1,28

Табл. 3. Параметры фокусного пятна для призмы из титаната бария (n=1,8)

h trian , мкм	I max , отн.ед.	FWHMx, λ	f , мкм	DOF, λ
15,03	6,08	0,60	16,10	6,00
16,03	8,01	0,54	12,80	4,75
17,03	8,05	0,43	9,40	3,83
17,23	9,02	0,43	9,09	3,83
18,04	6,70	0,40	6,23	2,63
19,04	8,11	0,40	4,80	2,40
19,44	6,50	0,40	3,80	2,15
20,04	5,14	0,38	2,22	1,63
21,04	4,20	0,25	0	1,03

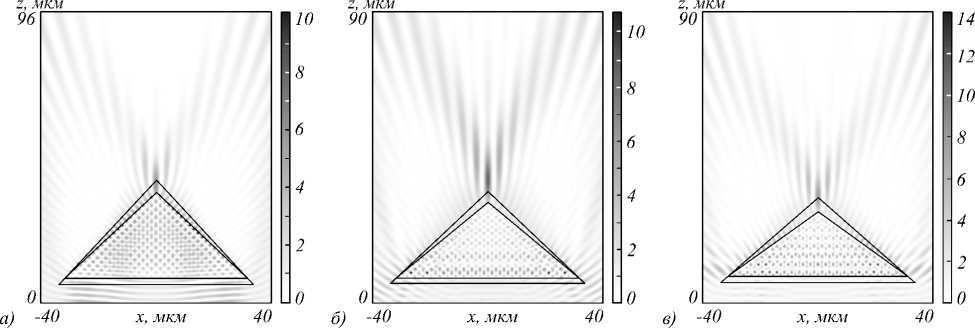
Рис. 8. Двумерное распределение интенсивности при фокусировке света диэлектрической треугольной призмой из кварцевого стекла (а), полистирола (б) и титаната бария (в)

Из табл. 2, 3 видно, что, как и в случае с кварцевым стеклом, удается сформировать пятна с размерами меньше скалярного дифракционного предела. В случае, если максимум интенсивности фокусного пятна располагается в свободном пространстве, наименьшая ширина фокусного пятна равна 0,38 λ. Если же максимум интенсивности смещен внутрь призмы, то ширину удается уменьшить до FWHM = 0,25 λ (призма из титаната бария с высотой 21,04 мкм).

Влияние длины волны фокусируемого света на параметры фокусного пятна

Исследуем теперь, как изменение длины волны повлияет на результаты фокусировки, для этого будем освещать призму из кварцевого стекла светом с длиной волны 3 мкм и 5 мкм. Результаты фокусировки призмой с шириной основания 60 мкм приведены в табл. 4 и 5. Для сравнения в табл. 6 приведены результаты аналитического решения дифракции плоской ТЕ-поляризованной волны на цилиндре с диаметром 60 мкм.

Табл. 4. Зависимость характеристик фокусного пятна от высоты призмы из кварцевого стекла (n=1,46), освещаемой светом с длиной волны 3 мкм

h trian , мкм	I max , отн.ед.	FWHMx, λ	f , мкм	DOF, λ
22,6	7,93	0,60	15,3	7,7
23,4	8,80	0,60	13,1	6,7
24,0	8,90	0,53	11,5	5,8
24,3	9,10	0,53	10,8	5,3
24,5	9,20	0,50	10,0	5,8
25,4	9,48	0,53	7,8	4,2
26,8	8,92	0,47	4,7	3,2
28,2	6,30	0,40	2,4	2,0
28,5	6,59	0,40	2,2	2,3
29,0	5,61	0,30	0,2	1,5

Из сравнения табл. 1, 4–6 видно, что призма формирует фокусное пятно с меньшими размерами. Более того, использование призмы приводит к меньшей зависимости ширины фокусного пятна от длины волны фокусируемого света: в табл. 6 ΔFWHM = 0,09 λ, а в табл. 4, 5 ΔFWHM в среднем было равно 0,05 λ. При этом для некоторых значений высоты призмы, например 28,2 мкм, для всех длин волн 3, 4 и 5 мкм ширина пятна совпадает FWHM = 0,4 λ. Стоит, однако, заметить, что ширина пятна по-прежнему остается пропорциональной длине волны λ и меньше становится только коэффициент пропорциональности.

Табл. 5. Зависимость характеристик фокусного пятна от высоты призмы из кварцевого стекла (n=1,46), освещаемой светом с длиной волны 5 мкм

h trian , мкм	I max , отн.ед.	FWHMx,λ	f , мкм	DOF,λ
22,6	7,57	0,60	16,0	5,2
23,4	7,74	0,60	13,4	4,8
24,0	7,80	0,58	11,8	4,2
24,3	7,73	0,56	11,0	4,2
24,5	7,69	0,60	10,5	4,0
25,4	7,81	0,60	8,8	3,5
26,8	7,00	0,48	6,1	3,3
28,2	5,37	0,40	3,2	2,4
28,5	5,43	0,40	3,0	2,4
29,0	6,29	0,38	2,3	2,2

Табл. 6. Ширина и глубина фокусного пятна, формируемого цилиндром из кварцевого стекла с диаметром 60 мкм

λ, мкм	FWHMx, λ	DOF, λ
3	0,64	3,81
4	0,60	3,25
5	0,55	2,69

Заключение

Было показано, что двумерные треугольные призмы позволяют фокусировать свет в свободном пространстве в пятна с размерами меньше скалярного дифракционного предела. В частности, призма из кварцевого стекла с шириной основания 60 мкм и высотой 28,5 мкм формирует фотонную нанострую с максимальной интенсивностью, в 6 раз превышающей интенсивность падающего излучения, и шириной FWHM = 0,38 λ. А призма из титаната бария с шириной основания 60 мкм и высотой 20 мкм позволяет получить фотонную нанострую с такой же шириной (0,38 λ) и максимальной интенсивностью, в 5 раз превышающей интенсивность падающего излучения. Размеры фокусного пятна можно уменьшать и дальше, если высота призмы подобрана таким образом, чтобы максимум интенсивности располагался внутри призмы. Так, например, призма из титаната бария с высотой 21 мкм и шириной основания 60 мкм формирует фокусное пятно с шириной FWHM = 0,25 λ.

Было показано, что использование призмы приводит к меньшей зависимости ширины фокусного пятна от длины волны фокусируемого света по сравнению с микроцилиндром: так, например, у микроцилиндра из кварцевого стекла с диаметром 60 мкм смена длины волны с 3 мкм до 5 мкм приводит к изменению ширины пятна на 0,09 λ, а у призмы – в среднем на 0,05 λ.

Работа выполнена при поддержке Российского Фонда Фундаментальных Исследований – грант 18-

07-01122 в части «Фокусировка излучения треугольной призмой из кварцевого стекла», грант 18-0701380 в части «Фокусировка излучения круглым цилиндром» и грант 18-29-20003 в части «Влияние показателя преломления на параметры фокусного пятна», и Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН в части «Введение».