Формирование и особенности напряжённо-деформированного состояния бетонного экрана каменно-набросной плотины

Каменно-набросные плотины с бетонным экраном (КПБЭ) являются одним из наиболее перспективных типов плотин для строительства высоконапорных гидроузлов. В разных странах мира построено несколько сверхвысоких КПБЭ (высотой 200 м) [1,2].

Однако КПБЭ обладают существенным недостатком – недостаточная надёжность бетонного экрана (БЭ). На ряде плотин происходили аварийные ситуации, связанные с образованием структурных трещин в БЭ. Примерами могут служить плотины Xingo, Tianshengqiao-1, Ita и Itapebi, Mohale, Barra Grande, Campos Novos, Buxi [3-9].

Образование трещин в БЭ создаёт угрозу безопасности плотины, поэтому актуальным вопросом гидротехнической науки является изучение причин их возникновения. Ряд научных работ посвящены анализу напряжённо-деформированного состояния и научному обоснованию конструкций КПБЭ [1, 11-14]. Однако до сих пор в проектной практике господствуют умозрительные представления о работе КПБЭ, а их проектирование ведётся на основе эмпирического подхода [5-6, 15-17].

Простейшая умозрительная схема работы БЭ предполагает, что экран работает только на поперечный изгиб, который возникает из-за уплотнения тела плотины под действием гидростатического давления. Прогиб экрана происходит в сторону нижнего бьефа, поэтому при изгибе верховая грань экрана испытывает сжатие, а низовая – растяжение. При изгибе значения сжимающих и растягивающих напряжений в БЭ одинаковы по модулю. Основную опасность представляют растягивающие напряжения, т.к. у бетона прочность на растяжение существенно меньше, чем на сжатие.

Значения напряжений на гранях могут быть приближённо определены по известным формулам сопротивления материалов через прогиб экрана:

σ=± M =± E б J =± tE б =± 4E б tf _.

W WR 2 R    L2

Здесь E б – модуль линейной деформации бетона экрана;

M – изгибающий момент в сечении экрана;

J, W – соответственно момент инерции и момент сопротивления поперечного сечения экрана; t – толщина экрана;

L, f – соответственно длина и прогиб экрана;

L2

R =     – радиус кривизны экрана при заданном прогибе.

8f

Для оценки влияния изгиба на НДС экрана рассмотрим на примере сверхвысокой плотины высотой 200 м с заложением верхового откоса 1,4. Принимая толщину экрана равной 1 м, прогиб экрана равным 1,0 м, а E б =30 ГПа, получим значения напряжений равными

4 ⋅ 30000 ⋅ 1 ⋅ 1,0 σ=±

1,0 МПа.

Растягивающее напряжение величиной в 1 МПа не превосходит расчётное сопротивление бетона класса B30 на растяжение по предельным состояниям второй группы, которое составляет 1,8 Мпа [24]. Т.е. образование в экране поперечных трещин не произойдёт.

В рассмотренной простейшей схеме работы БЭ не учитывается наличие у экрана собственного веса. В современных плотинах для обеспечения создания в экране сжимающего давления от собственного веса предусматривают мероприятия по снижению трения на контакте экрана с телом плотины [15-17]. Cовременная технология возведения КПБЭ предусматривает формирование поверхности верхового откоса под экран из бетонных блоков. Во избежание сцепления между экраном бетонной подготовкой на контакте между ними укладывается слой битумной мастики.

Если считать, что трение и сцепление на контакте экрана с телом плотины мало, то продольное сжимающее давление на подошве экрана от собственного веса составит

σ= γб Hsinα, здесь γб – удельный вес бетона (около 24 кН/м3); H – высота плотины;

α – угол наклона верхового откоса плотины.

Это давление имеет существенно по величине. Например, для плотины высотой 200 м оно составляет около 2,8 МПа.

В рассмотренном случае сжимающее давление от собственного веса экрана превышает растягивающее напряжение от изгиба, поэтому трещиностойкость экрана обеспечена.

Рассмотренный пример хорошо иллюстрирует господствующие умозрительные представления о НДС экрана. Считается, что сжимающее давление от собственного веса БЭ способно «задавить» (компенсировать) большую часть растягивающих напряжений от изгиба и что маловероятно возникновение в экране существенных по величине растягивающих напряжений. Армирование плиты БЭ производят сеткой, расположенной по её средней линии, оно предназначено только для восприятия температурновлажностных деформаций. В некоторых источниках можно встретить утверждения, что БЭ находится в состоянии двухосного сжатия [16].

Однако такое представление о работе КПБЭ не объясняет факты образования в экране поперечных структурных трещин. Поэтому при анализе аварийных ситуаций образование трещин связывают с неравномерностью деформаций изгиба плиты экрана [3,18].

В [3] неравномерность деформаций изгиба плит объясняют сложными топографическими условиями створа. Мори в [16] утверждает, что области возникновения структурных трещин приурочены к местам нарушения целостности подэкрановой зоны и к зонам, где сопрягаются разные по своей деформируемости грунты. Неравномерные деформации изгиба экрана могут быть также вызваны сложной последовательностью возведения плотины. Об этом свидетельствуют факты образования горизонтальных трещин в экране плотин Tianshengqiao-1 [11] и Buxi [9].

Однако в реальности схема работы БЭ гораздо более сложная, чем в умозрительных моделях. В работе [3] Marques и Pinto ещё в 2005 г. высказали предположение о том, что через трение по грунту на БЭ могут передаваться растягивающие продольные силы. Arici в [12] с помощью численного моделирования показал, что нижняя часть экрана испытывает растягивающие продольные силы, ещё ранее аналогичный результат был получен автором [19].

Методические исследования автора [20-21] показали, что образование в нижней части экрана растягивающих продольных сил неизбежно практически в любых условиях. В [21] автором было показано, что чем ниже деформируемость каменной наброски, тем меньшую роль в формировании НДС БЭ играют деформации изгиба и тем бóльшую роль – продольные силы. Это позволяет утверждать, что основную опасность для трещиностойкости экрана представляют не деформации изгиба, а растягивающие продольные силы, вызванные трением по грунту.

Эти исследования позволили автору сформулировать новое теоретическое представление о формировании НДС БЭ [20]. Оно заключается в том, что экран работает не только на изгиб, но и на восприятие продольных сил. Аналогичное мнение высказано в работе [1], где приведены натурные данные о растягивающих напряжениях в экранах КПБЭ. В [1] подчёркивается, что растяжение в направлении вдоль откоса вызвано не только изгибом, но и растягивающей продольной силой.

Однако в данных исследованиях не учитывалось устройство под экраном бетонной подготовки и антифрикционного слоя на контакте между ними. Отдельное выполненное автором исследование [22] показало, что наличие бетонной подготовки и снижающего трения слоя вносит некоторые коррективы в НДС экрана, однако эти изменения невелики. Незначительное влияние сдвиговых характеристик контакта объясняется тем, что касательные напряжения на контакте довольно малы, чтобы вызвать проскальзывание экрана. Было показано, что использованные в [19-21] упрощающие допущения не сильно искажают условия работы БЭ.

Тем не менее, наличие этих допущений может вызвать сомнения в сделанных выводах. Поэтому было решено уточнить результаты исследований, использовав более точную расчётную схему. Результатам исследований посвящена данная статья.

Целью исследования являлось определение условий формирования НДС БЭ и выявление роли трения в этом процессе. Оно должно дать новые знания о работе КПБЭ, без которых сложно формулировать рекомендации по повышению надёжности БЭ.

Методы

Исследования проводились на примере плотины высотой 100 м с заложением откосов 1,3 (рис.1). НДС плотины определялось с помощью численного моделирования методом конечных элементов. Использовалась вычислительная программа, составленная автором [23].

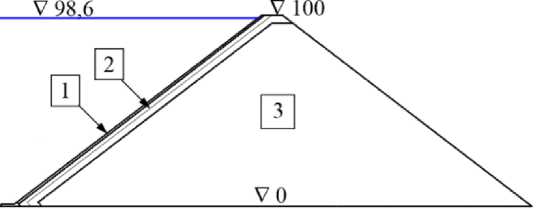
Рис.1 Схема конструкции каменно-набросной плотины с бетонным экраном. 1 – бетонный экран, 2 – подэкрановая зона, 3 – упорная призма

Составленная конечно-элементная модель поперечного сечения плотины включала 871 конечный элемент сплошной среды. Периметральный шов и контакт экрана с телом плотины моделировались с помощью 106 конечных элементов типа Goodman. Предусматривалась возможность потери прочности контакта на растяжение и сдвиг. Использование кубической степени аппроксимации перемещений позволило довольно точно воспроизвести сложный характер работы БЭ и его взаимодействия с телом плотины. Общее количество степеней свободы в модели составило 8586.

Методика исследований предусматривала рассмотрение ряда вариантов, каждый из которых выражал влияние одного из факторов, определяющих НДС плотины.

Первый фактор – это расчётная схема (устройство) конструкции плотины. Рассматривались три расчётные схемы (варианта).

• 1.    Условная расчётная схема, которая не учитывает устройство подэкрановой подготовки из малоцементного бетона. Параметры сдвиговой прочности контакта экрана с телом плотины принимались соответствующими контакту бетона и каменной наброски.

• 2.    Расчётная схема, соответствующая конструкции плотины, в которой бетонная подэкрановая подготовка выполняется на всём протяжении экрана. Параметры сдвиговой прочности контакта учитывали укладку между экраном и бетонной подготовкой слоя битумной мастики.

• 3.    Расчётная схема, воспроизводящая реальные условия работы плотины. Принималось, что бетонная подэкрановая подготовка выполняется по всей длине верхового откоса за исключением его самой нижней части [22].

Второй фактор – это деформируемость тела плотины. Строение плотины принималось однородным, т.е. не делалось различия между деформируемостью каменной наброски в упорной призме и в подэкрановой зоне. При исследованиях грунты тела плотины считались линейно-деформируемыми. Исследования проводились для широкого диапазона значений параметров модели, что обеспечивает уверенность в достоверности результатов исследования. Модуль линейной деформации E к каменной наброски варьировался от 60 до 480 МПа. Этот диапазон значений соответствует деформируемости каменной наброски в теле реальных плотин. Коэффициент Пуассона V k каменной наброски варьировался от 0 до 0,3.

Для бетона экрана модуль линейной деформации принимался равным E б =29 ГПа, коэффициент Пуассона V 6 =O,2.

Для контакта между бетоном и каменной наброской принимались следующие параметры сдвиговой прочности: удельное сцепление равно 0, угол внутреннего трения 45°, касательная жёсткость 200 МПа/м. Для контакта, разъединённого битумной эмульсией, принималось: удельное сцепление 20 кПа, угол внутреннего трения 10°, касательная жёсткость 50 МПа/м.

Расчёты проводились на нагрузки собственного веса и гидростатического давления. Моделировалась самая простая схема последовательности возведения сооружения и нагружения его внешними силами. Сначала воспроизводилась послойная отсыпка каменная наброска, затем укладка каменной наброски, а потом – постепенное наполнение водохранилища.

Результаты и обсуждение

Анализ результатов решения задачи НДС проводился не только по величинам перемещений и напряжений экрана – по напряжениям вычислялись продольные силы и изгибающие моменты в сечениях БЭ. Результаты исследований позволили выявить условия формирования НДС КПБЭ.

Исследования НДС КПБЭ без учёта жёсткой подэкрановой подготовки

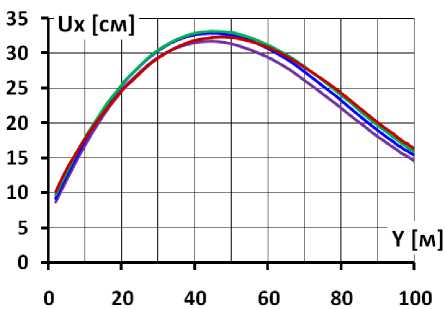
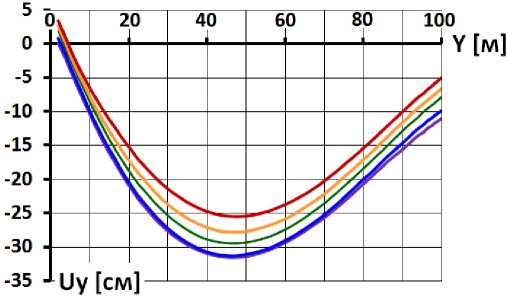
По результатам расчётов до наполнения водохранилища перемещения экрана невелики, но затем, под действием гидростатического давления получает существенные перемещения. На рис.2 показан пример распределения перемещений экрана для случая, когда модуль линейной деформации каменной наброски E к составляет 60 МПа. Видно, что осадки (рис.2б) и горизонтальные смещения (рис.2а) имеют примерно одинаковый характер распределения по высоте. В нижней половине наблюдается увеличение перемещений с ростом высоты, а в верхней – их уменьшение. Это говорит об изгибе экрана в сторону нижнего бьефа.

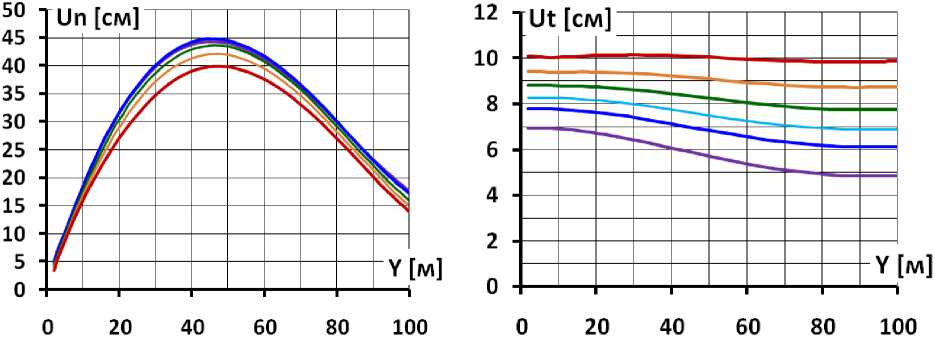
Изгиб экрана иллюстрирует также распределение по высоте поперечных перемещений U n экрана, т.е. перемещений в направлении, перпендикулярном к откосу (рис.2в). Поперечные перемещения достигают максимума на высоте примерно 45 м, т.е. примерно посередине высоты плотины. При E к =60 МПа максимальные прогибы экрана находятся в интервале от 39,7 до 44,8 см в зависимости от значения коэффициента Пуассона V k . При этом нарастание поперечных перемещений по высоте в верхней части происходит более интенсивно, чем их снижение в нижней части. Соответственно, изгиб нижней части экрана выражен сильнее, чем в верхней.

Одной из важных характерных особенностей НДС БЭ является то, что экран приобретает перемещения не только в поперечном направлении, но и в направлении вдоль откоса (рис.2г). Это связано с тем, что абсолютные величины перемещений осадок и смещений экрана также примерно одинаковы. Т.к. угол наклона откоса меньше 45°, продольные перемещения положительны по величине по всей высоте.

В самой нижней части экрана, в периметральном шве, продольное перемещение экрана не равно 0 (рис.2г). Это говорит о наличии раскрытия периметрального шва. Данный результат численного моделирования подтверждается тем, что по данным натурных наблюдений периметральный шов раскрывается [15].

а)                                                   б)

в)                                                               г)

О —0.1 —0.15 —0.2 —0.25 —0.3

Рис. 2. Перемещения железобетонного экрана при модуле линейной деформации каменной наброски 60 МПа и различных вариантов каменной наброски

Однако на разных высотах соотношение величин осадок и смещений не является постоянным. Это приводит к тому, что величины продольные перемещения изменяются по высоте, они могут как возрастать, так и уменьшаться.

Исследование выявило, что НДС во многом зависит от коэффициента Пуассона каменной наброски ν к . Расчёт показал, что величина ν к мало влияет на величины смещений, но оказывает существенное влияние на осадки экрана. В диапазоне изменения ν к от 0 до 0,3 максимальное смещение изменяется в интервале 31,7÷33,2 см, при чём максимальное значение достигается при ν к =0,15 (рис.2а). В то же время максимальная осадка экрана при ν к =0 составляет 31,5 см, то при ν к =0,3 – 25,4 см (рис.2б), чем больше ν к , тем меньше осадки.

Из-за уменьшения осадок экрана с ростом ν к его продольные перемещения уменьшаются (рис.2г). При этом изменяется и характер распределения продольных перемещений вдоль откоса. При ν к =0,3 продольные перемещения экрана изменяются в узких пределах (0,31 см) и приблизительно равны 10 см (рис.2г). При этом в нижней части экрана (до ∇29 м) имеется участок увеличения продольных перемещений, а в верхней части (от ∇29 м до ∇90 м) – их уменьшения. При меньших значениях ν к увеличивается диапазон изменения величин продольных перемещений, а также изменяется характер распределения по высоте. При ν к =0 величины продольных перемещений уменьшаются с высотой на 2,1 см.

Описанная неравномерность в распределении продольных перемещений вызывает в экране линейные деформации продольного удлинения-укорачивания. Из-за высокой жёсткости бетона едва заметные изменения линейных деформаций вызывают существенные продольные силы. Эти продольные силы передаются на экран через трение относительно тела плотины.

В зависимости от уровня водохранилища характер распределения касательных напряжений τ на контакте экрана с плотиной существенно изменяется. До наполнения водохранилища касательные напряжения определяются только собственным весом БЭ. Часть веса БЭ передаётся на бетонную контурную плиту и вызывает сжатие периметрального шва, а другая часть – воспринимается касательными напряжениями на контакте БЭ и грунтовой плотины. Эпюра касательных напряжений имеет треугольную форму, своего максимума они достигают внизу. Суммарная сила, воспринимаемая касательными напряжениями на контакте, составляет около четверти от полного веса экрана.

После восприятия сил гидростатического давления происходит увеличение и перераспределение касательных напряжений τ на контакте БЭ и плотины. На рис.3 показано распределение τ для момента полного заполнения водохранилища. В этот момент из-за больших горизонтальных смещений плотины периметральный шов раскрывается, поэтому весь вес БЭ целиком воспринимается касательными напряжениями τ. Площадь эпюры τ соответствует проекции весу БЭ на наклонную поверхность верхового откоса.

Для распределения касательных напряжений на контакте БЭ с плотиной характерно крайне неравномерное распределение. Эпюра τ – знакопеременная, а их величины резко увеличиваются по сравнению с моментом до наполнения. В эпюре можно выделить три участка (рис.3). В верхней части контакта τ действуют на экран в направлении снизу вверх, они имеют положительный знак. В средней части контакта касательные напряжения направлены сверху вниз, т.е. имеют отрицательный знак. На самом нижнем, очень коротком, участке τ снова положительны и достигают значительных величин (десятые доли МПа). Своего максимума по абсолютной величине напряжения τ достигают в самой нижней точке контакта.

Характер распределения касательных напряжений оказывает очень большое влияние на НДС БЭ. Наличие на контакте отрицательных касательных напряжений τ вызывает в экране появление сжимающей продольной силы, а положительных τ – растягивающей силы.

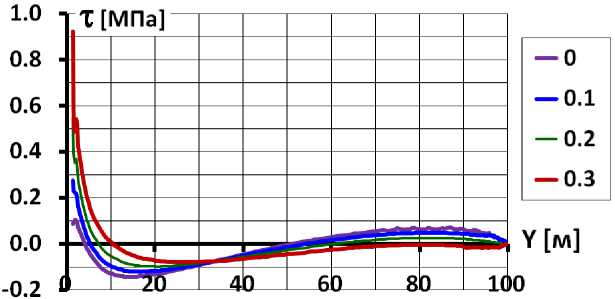
Рис.3 Распределение по высоте касательных напряжений на контакте экрана с грунтом (после восприятия гидростатического давления)

Анализ напряжённого состояния показал, что главные напряжения, действующие в экране, имеют направления, связанные с наклоном экрана. Одно из главных напряжений действует в направлении вдоль экрана, а другое – поперёк откосу. Главное напряжение, действующее в направлении поперёк откоса, соответствует гидростатическому давлению. Интерес представляет главное напряжение, действующее в направлении, близком, к направлению вдоль откоса.

Распределение напряжений в направлении вдоль экрана (т.е. продольные напряжения) определяются двумя фактором: трением на контакте экрана и плотины, а также изгибом экрана. Для выявления влияния трения был проведён дополнительный расчёт для случая, когда касательная жёстокость контакта экрана с плотиной близка к 0. В этом случае НДС БЭ определяется только деформациями изгиба. Модуль каменной наброски принимался равным 60 МПа, а коэффициент Пуассона – 0,25. На рис.4 показано распределение продольных напряжений, полученное расчётом для обоих случаев.

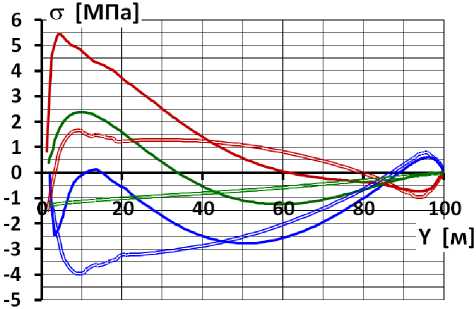
верховая грань (с трением) низоваягрань(стрением) средняя (с трением) верховая грань(без трения) низоваягрань(безтрения) среднее (безтрения)

Рис.4 Распределение продольных напряжений в экране на момент окончания наполнения водохранилища

В случае отсутствия трения на контакте продольные напряжения по средней линии БЭ определяются только собственным весом экрана. Они сжимающие и увеличиваются сверху вниз (рис.4). За счёт деформаций изгиба на низовой грани экрана происходит уменьшения сжатия, а на верховой грани – его увеличение. При принятом модуле каменной наброски деформации изгиба вызывают значительную неравномерность распределения напряжений между гранями, которая превышает напряжения от продольной силы. По этой причине продольные напряжения на низовой грани являются растягивающими (за исключением самой верхней части экрана, где изгиб происходит в сторону верхнего бьефа). Своего максимума растягивающие напряжения достигают в самой нижней части экрана и составляют 1,7 МПа. Это значение не превышает расчётного сопротивления бетона класса B30 на растяжение.

В случае наличия трения на контакте для НДС БЭ характерно действие значительных продольных сил. Об этом свидетельствует распределение напряжений по средней линии экрана (рис.4). В нижней части экрана (ниже ∇34м) средние напряжения – растягивающие, они достигают 2,4 МПа. В верхней части средние напряжения – сжимающие, при этом они выше, чем в случае отсутствия трения на контакте. Наличие растягивающей продольной силы в нижней части экрана делает его НДС крайне неблагоприятным. Максимальное значение растягивающего напряжения достигает 5,5 МПа, оно много больше расчётного сопротивления бетона на растяжение, что говорит о неизбежности образования трещин в БЭ.

Для анализа по значениям напряжений на гранях были вычислены значения изгибающих моментов (рис.5). Изгибающие моменты достигают максимума в нижней части экрана (на ∇4÷9м), а затем уменьшаются с высотой. Было выявлено, что наличие касательных напряжений на контакте экрана с телом плотины вызывает изменение изгибающих моментов. Если в случае отсутствия трения максимальное значение изгибающего момента составляет 0,46 МН · м, то с учётом трения – 0,62 МН · м, т.е. увеличилось на треть. Наибольшие изменения наблюдаются в самой нижней части экрана, на участке длиной около 8 м. Увеличение изгибающих моментов на локальном участке является следствием продольного изгиба, т.е. изгибом, вызванного эксцентриситетом продольной силы.

Таким образом, установлено, что БЭ испытывает продольно-поперечный изгиб .

Учитывая, что наличие трения на контакте БЭ с каменной наброской негативно сказывается на трещиностойкость экрана, дальнейшей задачей исследования была выявление влияния деформируемости каменной наброски на НДС контакта и НДС БЭ.

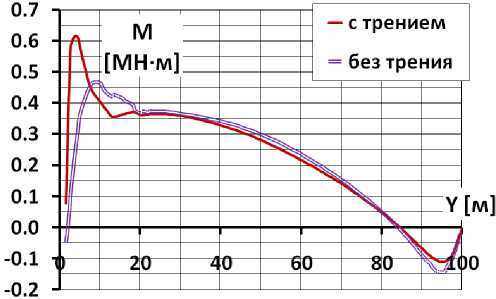
Рис.5 Распределение значений изгибающего момента по высоте экрана

В результате исследования было выявлено, что модуль деформации каменной наброски E к очень мало влияет на характер распределения и величины касательных напряжений на контакте БЭ и плотины. НДС контакта в бóльшей степени определяется коэффициентом Пуассона ν к каменной наброски. При снижении ν к уменьшается длина нижнего участка высоких касательных напряжений τ, а сами величины τ резко снижаются. Благодаря этому при низких значениях ν к уменьшаются растягивающие продольные силы в БЭ.

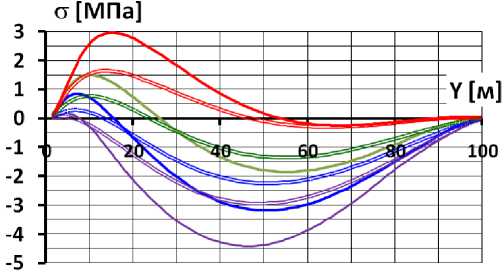
На рис.6 и 7 показаны результаты расчёта НДС для двух вариантов значений каменной наброски: 60 МПа и 480 МПа. На рис.6 показаны напряжения, полученные расчётом, по которым были вычислены значения продольных сил (которые численно соответствуют средним напряжениям σ) и изгибающих моментов (рис.7).

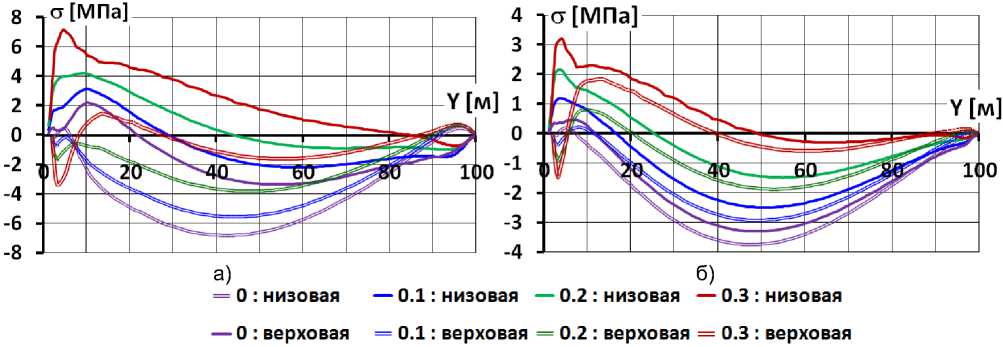
Рис.6 Распределение по высоте напряжений на гранях экрана для различных вариантов каменной наброски (вариант 1)

а – при модуле каменной наброски 60 МПа; б – при модуле каменной наброски 480 Мпа

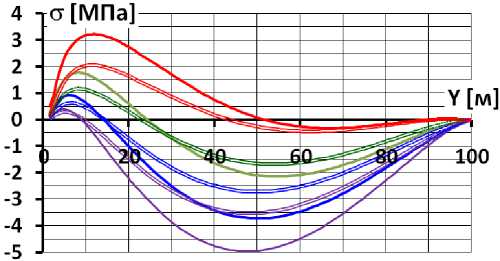
а)                                                      б)

— E=60 v=0 — Е=60 v=0.1 — Е=60 v=0.2 — Е=60 v=0.3

= Е=480 v=0 = Е=480 v=0.1 = Е=480 v=0.2 = Е=480 v=0.3

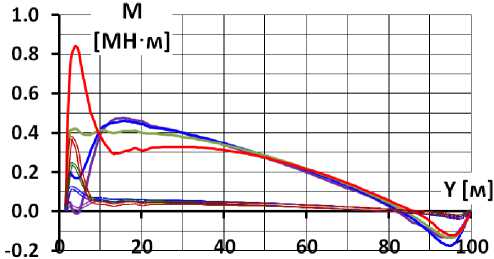
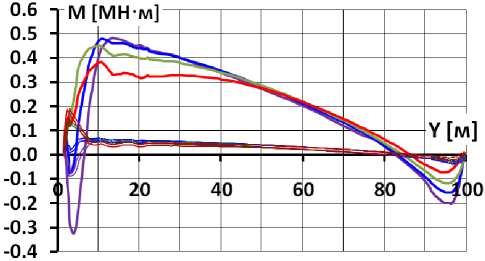
Рис.7 Распределение по высоте экрана продольных сил (а) и изгибающих моментов (б) для различных вариантов каменной наброски (вариант 1)

На рис.7а видно, что характер распределения продольных сил определяется значением коэффициента Пуассона ν к , а их величина – значением модуля линейной деформации E к . При ν к =0,3 на большей части длины экран испытывает растягивающие продольные силы. При этом они достигают значительных величин. При E к =60 МПа максимальное значение σ составляет 3,2 МПа, а при E к =480 МПа – 2,2 МПа. При уменьшении ν к длина зоны растягивающих продольных сил сокращается. При ν к =0 она уменьшается до 10 м. Значительно уменьшаются и максимальные значения σ. При E к =60 МПа максимальное значение σ составляет 0,39 МПа, а при E к =480 МПа – 0,29 МПа. Таким образом, в нижней части экрана из-за наличия продольных растягивающих сил создаются неблагоприятные условия для обеспечения трещиностойкости экрана.

Это подтверждает рис.6а, который показывает, что при E к =60 МПа и любом значении ν к растягивающие напряжения на низовой грани экрана превышают расчётное сопротивление бетона растяжение. При E к =480 МПа и при ν к >0,15 прочность бетона на растяжение также не обеспечивается (рис.6б). Т.к., как правило, для реальной каменной наброски коэффициент Пуассона ν к >0,15, а значения модуля E к <300 МПа, трещиностойкость экрана обеспечить очень сложно.

Однако следует отметить, что возникающая в варианте с ν к =0,3 область высоких растягивающих напряжений располагается только в нижней части экрана и имеет локальные размеры. Её образование вызвано резким увеличением изгибающих моментов M на данном участке (рис.7б). Причиной скачка M является продольный изгиб экрана. В то же время при ν к <0,2 этот скачок M отсутствует вовсе. Анализ графиков распределения изгибающих моментов показывает, что характер распределения определяется значением коэффициента ν к , а их величины – значением E к .

Исходя из анализа влияния деформативных характеристик каменной наброски (E к и ν к ) на величины и характер распределения продольных сил N и изгибающих моментов M, можно сделать следующие выводы:

• •    Характер распределения N и M определяется в основном значением E к , а их величины – значением ν к ;

• •    Коэффициент Пуассона ν к сильнее влияет на НДС БЭ, чем E к . Для обеспечения благоприятного НДС предпочтительным является снижение ν к до минимума. Однако в реальных условиях ν к не принимает тех значений, которые бы обеспечили прочность БЭ;

• •    Величина модуля линейной деформации каменной наброски E к сильнее влияет на M, чем на N. Увеличение E к в 4 раза снижает N примерно на треть, а M – примерно в 2 раза. Поэтому при высоких значениях E к опасность для трещиностойкости экрана растягивающие продольные силы представляют бóльшую опасность, чем деформации изгиба (изгибающие моменты);

• •    Можно сделать высказать предположение, что для улучшения НДС в нижней части экрана необходимо либо уменьшить усилия, передаваемые через трение на данном участке, либо укладывать материал с ν к <0,2.

Исследования НДС КПБЭ с жёсткой подэкрановой подготовкой на всю длину

В данной расчётной схеме на всём протяжении под экраном устраивается бетонная подэкрановая подготовка и они отделяются друг от друга слоем «смазки» из битумной эмульсии.

Расчёты показали, что устройство бетонной подготовки очень мало сказывается на поперечные перемещения экрана. Отличием НДС от расчётной схемы № 1 является то, что устройство слоя битумной смазки ограничивает величины касательных напряжений τ на контакте экрана с плотиной. В самой нижней части контакта при ν>0,15 происходит потеря сдвиговой прочности. При этом происходит перераспределение касательных напряжений на всём протяжении контакта (рис.8).

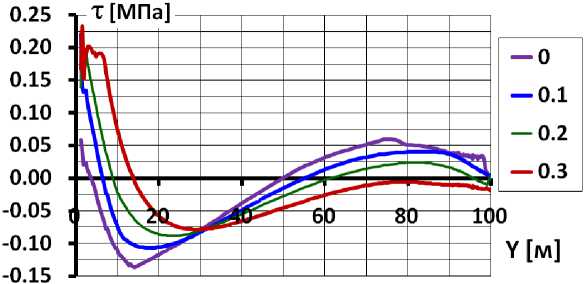
Рис.8 Распределение по высоте касательных напряжений на контакте экрана с подэкрановой подготовкой (вариант 2, после восприятия гидростатического давления)

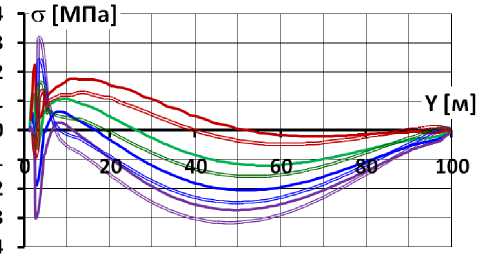
Перераспределение касательных напряжений τ оказывает благоприятное влияние на напряжённое состояние БЭ. В его нижней части уменьшаются растягивающие продольные напряжения на низовой грани

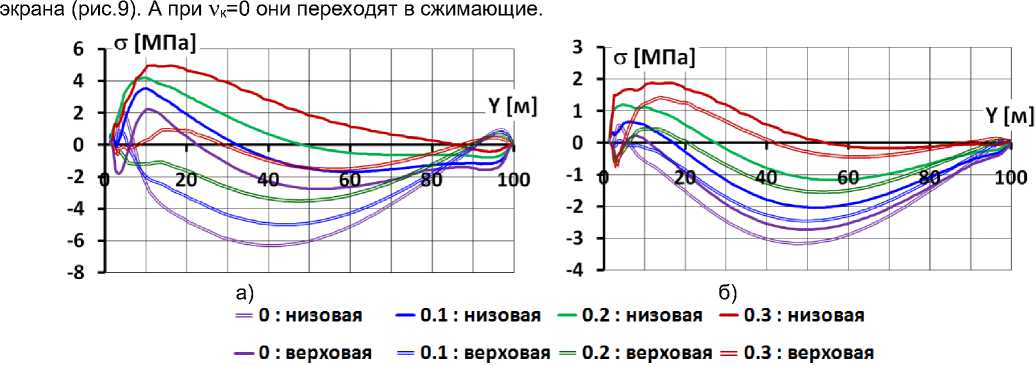
Рис.9 Распределение по высоте напряжений на гранях экрана для различных вариантов каменной наброски (вариант 2)

Благодаря этому в данном варианте НДС экрана несколько более благоприятное, чем в предыдущем. При этом следует подчеркнуть, что это происходит не благодаря устройству жёсткой подэкрановой подготовки, а благодаря устройству слоя смазки .

Улучшающие НДС изменения носят локальный характер и распространяются только на самый нижний, наиболее проблемный участок. Максимальные значения растягивающих продольных напряжений уменьшаются, но их уменьшение не имеют решающего значения для обеспечения трещиностойкости экрана.

На рис.10 показано распределение продольных сил (рис.10а) и изгибающих моментов (рис.10б) в БЭ для рассмотренного варианта. Их анализ показывает, что по сравнению с расчётной схемой №1 в схеме №2 уменьшаются как растягивающие, так и сжимающие продольные силы, но незначительно (рис.10а). Изменения изгибающих моментов свидетельствует об изменениях в деформациях изгиба нижней части экрана. Низкие показатели сдвиговой прочности контакта между бетонной подготовкой и наклонной гранью контурной плиты усиливают эффект проскальзывания на данном контакте и ведут к локальному, но очень незначительному повышению прогибов нижнего края плиты. Таким образом, в расчётной схеме 2 происходят изменения в поперечном и продольном изгибе нижнего края плиты экрана.

При ν к >0,15 изменения в изгибе экрана ведут к увеличению положительных значений изгибающих моментов (рис.10б), а при ν к <0,15 – к их снижению. При ν к =0 в нижней части изгибающие значения в нижней части экрана принимают отрицательные значения, т.е. экран выгибается в сторону верхнего бьефа.

• а)                                                         б)

— E=60 v=0 — Е=60 v=0.1 — Е=60 v=0.2 — Е=60 v=0.3

= Е=480 v=0 = Е=480 v=0.1 = Е=480 v=0.2 = Е=480 v=0.3

Рис.10 Распределение по высоте экрана продольных сил (а) и изгибающих моментов (б) для различных вариантов каменной наброски (вариант 2)

Исследования НДС КПБЭ для реальной схемы устройства жёсткой подэкрановой подготовки

Данная расчётная схема соответствует реальным условиям, когда бетонная подэкрановая подготовка устраивается не на всём протяжении – в самой нижней части (на длине около 2м) экран опирается на подэкрановую зону из грунта. Нижняя граница бетонной подготовки располагается на ∇2,4 м.

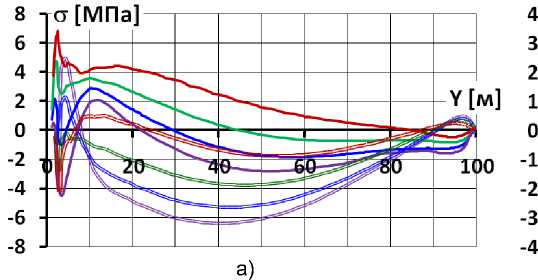
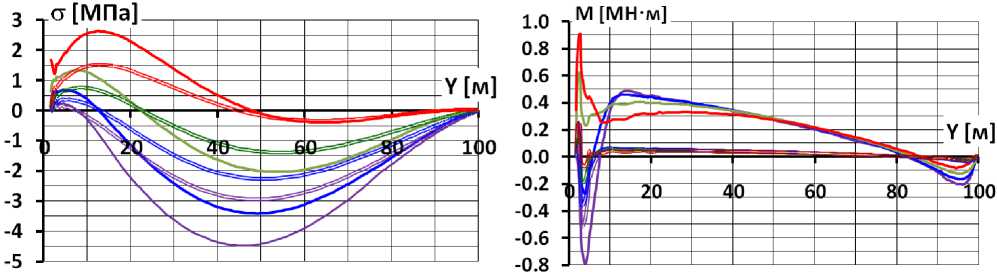
Численное моделирование НДС показало, что в данном варианте конструкции нижняя часть БЭ испытывает деформации изгиба сложного характера. Это связано с неравномерностью распределения поперечных перемещений экрана – на участке, где бетонная подготовка отсутствует, поперечные перемещения больше, чем там, где она есть. Из-за этого изгиба распределение продольных напряжений по длине экрана имеет знакопеременный характер (рис.11). Имеется 2 участка концентрации растягивающих напряжений. Первый участок располагается на ∇2÷2,5 м, а второй участок – на ∇3,5÷4,5 м. На первом растягивающие напряжения возникают на верховой грани, а на втором – на низовой грани. При этом на первом участке растягивающие напряжения тем выше, чем больше ν к , а на втором – наоборот. Это хорошо иллюстрирует рис.12б, на котором показано изменение изгибающих моментов по высоте экрана. На участке ниже ∇10 м происходят резкие и знакопеременные скачки изгибающих моментов, они иллюстрируют сложный характер деформаций изгиба.

• б)

= 0:низовая —0.1: низовая —0.2: низовая —0.3 : низовая

— О : верховая = 0.1: верховая = 0.2 : верховая = 0.3 : верховая

Рис.11 Распределение по высоте напряжений на гранях экрана для различных вариантов каменной наброски (вариант 3)

а – при модуле каменной наброски 60 МПа; б – при модуле каменной наброски 240 МПа

а)                                                        б)

Е=60 v=0 — Е=60 v=0.1 — Е=60 v=0.2 — Е=60 v=0.3

Е=480 v=0 = Е=480 v=0.1 = Е=480 v=0.2 = Е=480 v=03

Рис.12 Распределение по высоте экрана продольных сил (а) и изгибающих моментов (б) для различных вариантов каменной наброски (вариант 3)

Исследования показали, что в расчётной схеме № 3 при всех значениях ν к и E к максимум растягивающих напряжений в экране достигает или превышает расчётное сопротивление бетона на растяжение. Таким образом, в реальной конструкции БЭ, как правило, работает в более неблагоприятных условиях, чем в других рассмотренных вариантах. Это подтверждается фактами образования трещин в экранах плотин Ita и Itapebi, которые были расположены вблизи контакта со скальными бортами и ориентированы примерно параллельно им [3].

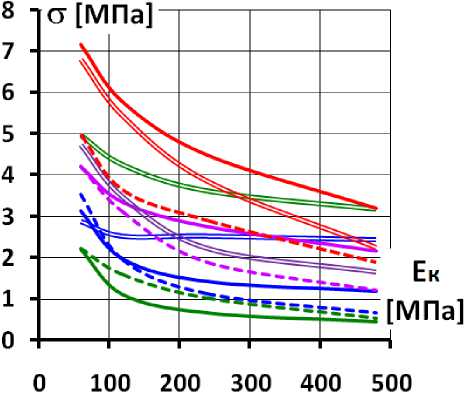
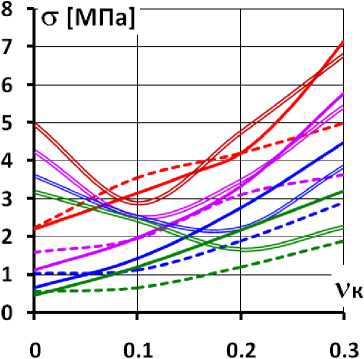
Влияние схемы устройства подэкрановой зоны на НДС экрана позволяют оценить обобщающие графики на рис.13-15. На рис.13,14 показано изменение максимальных значений растягивающих напряжений в БЭ для трёх рассмотренных расчётных схем в зависимости от E к и ν к . А на рис.15 – изменение максимальных значений продольных сил.

— О (вариант!) — О (вариант2) = О (вариантЗ) — 0.1 (вариант 1) — 0.1 (вариант 2) = 0.1 (вариантЗ) — 0.2 (вариант!) — 0.2 (вариант2) = 0.2 (вариантЗ) — 0.3 (вариант 1) — 0.3 (вариант2) = 0.3 (вариантЗ)

Рис.13 Изменение максимальных значений растягивающих напряжений в экране в зависимости от модуля линейной деформации каменной наброски.

Цифрами на графиках показаны значения коэффициента Пуассона каменной наброски

— 60 МПа (вариант 1) — 60 МПа (вариант2) = 60 МПа(вариантЗ)

—120 МПа (вариант!) — 120 МПа (вариант!)

120 МПа (вариантЗ) — 240 МПа (вариант!) — 240 МПа (вариант2) = 240 МПа (вариантЗ) — 480 МПа (вариант!) — 480 МПа (вариант2) = 480 МПа (вариантЗ)

Рис.14 Изменение максимальных значений растягивающих напряжений в экране в зависимости от коэффициента Пуассона каменной наброски.

Цифрами на графиках показаны значения модуля линейной деформации каменной наброски

Из рис.13 хорошо видно, что максимальная величина растягивающих напряжений в экране уменьшается с увеличением E к . Однако в большей степени она зависит от варианта конструкции подэкрановой зоны.

Использование варианта 2 (бордюрные блоки на всё протяжении экрана) во многих случаях позволяет снизить растяжение на 20÷40%. Наибольшее снижение наблюдается при ν к =0,3. Но при ν к =0 растяжение не уменьшается, а несколько увеличивается. Указанное снижение напряжений происходит несмотря на то, что за счёт уменьшения прогибов в нижней части экрана (в периметральном шве) увеличиваются деформации поперечного изгиба экрана. Это противоречие объясняется влиянием изменений касательных напряжений τ на контакте. Во-первых, за счёт снижения τ уменьшаются растягивающие продольных силы в экране (рис.15), а, во-вторых, происходит изменения знака продольного изгиба и изгибающего момента (рис.8).

Исследование показало, что чем меньше ν к , тем эффективнее применение бордюрных блоков на всё протяжении экрана.

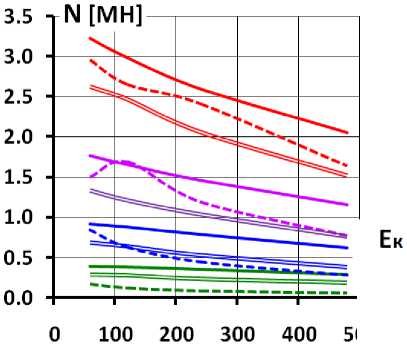
— О (вариант!) — О (вариант2) = О (вариант3) — 0.1 (вариант 1) — 0.1 (вариант 2) = 0.1 (вариант 3) — 0.2 (вариант 1) — 0.2 (вариант 2) = 0.2 (вариант 3) — 0.3 (вариант 1)

[МПа] —0.3 (вариант2) ^       = 0.3 (вариант 3)

Рис.15 Изменение максимальных значений продольных сил в экране в зависимости от модуля линейной деформации каменной наброски

Цифрами на графиках показаны значения коэффициента Пуассона каменной наброски

В варианте 3 (реальная схема работы экрана) растягивающие напряжения в БЭ могут как повышаться, так и снижаться по сравнению с вариантом 1. Это хорошо видно на рис.14. Как правило, при ν к <0,15 происходит повышение растягивающих напряжений по сравнению с вариантами 2 и 3. Наиболее неблагоприятные условия складываются при ν к =0, в этом случае растягивающие напряжения в несколько раз превышают расчётное сопротивление бетона на растяжение. Это повышение вызвано локальными деформациями изгиба.

При ν к >0,2 и E к >200 МПа в варианте 3 наблюдается снижение растягивающих напряжений примерно на 15÷30% по сравнению с вариантом 1 (рис.14). Снижение продольных сил более существенно по величине (рис.15).

Можно сделать вывод, что в реальной расчётной схеме (вариант 3, с устройством бордюрных блоков на неполную длину), НДС БЭ близко к условной схеме (вариант 1), в которой наличие бордюрных блоков не учитывается. Однако для варианта 3 характерна опасность возникновения трещин в БЭ из-за неравномерности деформаций изгиба на локальных участках. Можно рекомендовать выполнять бордюрные блоки на всём протяжении экрана за исключением зоны упора в скальное основание и контурную плиту. Там целесообразно уложить слой асфальтобетона.

Выполненное исследование позволило сформулировать рекомендации по определению характеристик каменной наброски плотины для плотины высотой 100 м, обеспечивающих отсутствие нарушений прочности бетона экрана на растяжение. Нами было выявлено, что эти рекомендации должны быть сформулированы во взаимосвязи модуля линейной деформации E к и коэффициента Пуассона ν к каменной наброски. Растягивающие напряжения в БЭ варианта 2 не превышают 1,8 МПа в следующих случаях: при E к =100 МПа и ν к =0, при E к =140 МПа и ν к =0,1, при E к =270 МПа и ν к =0,2, E к =500 МПа и ν к =0,3.

По полученным значениям видно, что обеспечить прочность бетона на растяжение довольно сложно – требуется очень качественное уплотнение каменной наброски. Реальная каменная наброска, как правило, имеет ν к >0,2, поэтому её модуль деформации E к должен быть не менее 270 МПа.

Возникает вопрос, почему в реальных плотинах высотой 100 м обычно не происходит образование поперечных трещин даже при меньшем качестве уплотнение каменной наброски. Это можно объяснить несколькими причинами.

Во-первых, это влияние пространственных условий, когда плотина возводится в неширокой долине. Скальные борта ограничивают горизонтальные смещения плотины, что уменьшает возможность появления растягивающих продольных усилий.

Во-вторых, это может быть объяснено отличием расчётных деформативных характеристик бетона от реальных. В соответствии с российскими строительными нормами значение модуля деформации бетона E=29 ГПа соответствует быстрому восприятию нагрузок, а при длительном действии нагрузок значение E уменьшается примерно в 2 раза. Соответственно, можно ожидать, что за счёт процессов релаксации напряжения в бетоне могут быть уменьшены.

продольных сил. Эти продольные силы могут быть как сжимающими, так и растягивающими. Наиболее неблагоприятное НДС экрана характерно для нижней части экрана, в которой действуют растягивающие продольные силы. Растягивающие продольные силы столь велики, что превышают сжимающее давление от собственного веса бетона экрана.