Формирование импульсов тока в неравновесной низкотемпературной аргоновой плазме атмосферного давления в системе «острие - плоскость»

Неравновесная плазма при атмосферном давлении используется во многих технологиях. Например, в предыонизации газа в лазерных установках, модификации поверхностных свойств и т.д. [1]. Резкая неоднородность поля в межэлектродном промежутке и локализация процессов около электродов затрудняет экспериментальное изучение кинетики протекающих здесь процессов. В настоящее время разработаны модели развития разряда с участием мета-стабильных атомов, и при этом расчетная кинетика электронов позволяет оценить константы элементарных процессов при определенных условиях развития разряда, с учетом электрон-электронных столкновений [2, 3]. Также широко известны основные элементарные процессы в аргоновой плазме [4-6]. Согласно оценке константы скоростей этих процессов, можно выделить процессы ионизации, ступенчатой ионизации, ассоциативной и пеннинговской ионизации с участием возбужденных и метастабильных атомов, а также реакции конверсии. В настоящей работе предлагается решение самосогласованной задачи, основыванной на совместном решении уравнения баланса частиц и уравнения Пуассона, с учетом выноса метастабильных и возбужденных атомов с разрядной области и изменения вида функции распределения электронов по энергиям (ФРЭЭ).

Проведено сравнение рассчитанных физических величин с экспериментальными значениями. При развитии разряда, инициированного в системе «острие ‒ плоскость» в атмосфере аргона, на начальной стадии имеются непрерывные импульсы тока. Исследована динамика его развития на основе представленной модели.

Модель развития разряда

Рассматривается модель, учитывающая образование и гибель возбужденных атомов и молекулярных ионов, на основе которой можно исследовать динамику развития элементарных процессов, а также интегральных характеристик развития разряда. Основными уравнени- ями в данной модели являются:

дпе       дпе   д2Оепе                               2         2

^ ^йге~Э^" + у^2  = ^аае ^ е ^ е ^{+ k} е ^пАг *п ^Пе ^{+ k}AiⁿAr m + к р[ П _Аг^ ^ —

• — Р еП^Аг * - an е n iA_T + ,

^Ре^Пе ^1Аг^{+и —}

^dn iAr ^{+    d(Vdrin} iAr⁺)

dt          дх

• ^— к _к0П п²п ₁А_Г +

= « ае У е П е + k * Па^ + k p^A ^ —P '_еПе П^П — Р е^п^

—

Arm

----m = k^nnp + аПрП;дг+-кр пл * пР-кд;Пл * -кР;Пл = st a e       e iAr2   e Arm e Ai Arm  Pi Ar

* m

dn.„ +

- A

^ⁿiAr+    ,    2

"^ = ^кА1^ПАг ^

—

аП е П ^Аг ^ + k _kon n²n _tA_T + ; j e = en e V dre j i = en iAr ⁺ V dri + en _iA_T + V _dri ; j = ] е +j i ; I = (j +js)S;

■ _   дЕ        _ ^е(n iAr ⁺⁺ⁿ iAr ⁺-ⁿ e )

js ~ £o dt; ^tvE ~        £o        , где n – концентрация атомов; De ‒ коэффициент диффузии электронов; ne ‒ концентрация электронов; niAr+ ‒ концентрация ионов Ar+; niAr2+ ‒ концентрация ионов Ar2+; je ‒ плотность электронного тока; ji ‒ плотность ионного тока; Vdri ‒ дрейфовая скорость ионов; Vdre ‒ дрей- фовая скорость электронов; в - коэффициент диэлектронной рекомбинации; ^е - коэффициент тройной рекомбинации; E ‒ напряженность электрического поля; I ‒ полный ток; js ‒ плот- ность тока смещения; S ‒ площадь токового сечения; e ‒ заряд электрона; ε0 ‒ электрическая постоянная; G - расход газа; moA - масса атома аргона; AV - объем разрядной области; аае - ионизационный коэффициент Таунсенда; kst - скорость возбуждения атома; ке - скорость ступенчатой ионизации; kAi - скорость ассоциативной ионизации; kPi - скорость пеннингов-ской ионизации; ау - скорость диссоциативной рекомбинации эксимеров Ar2+.

Система решается методом последовательных приближений сеточных уравнений с гра- ничными условиями:

и = 0,и =w, ia        , ec Y ia ’ где niс, neс ‒ концентрация ионов и электронов на катоде; γ ‒ коэффициент вторичной эмиссии; nia ‒ концентрация ионов на аноде.

Параметры, учитываемые в модели, определяются следующими аппроксимациями и численными значениями:

а у =8.5^10 -⁷Ш

0,67

см3/с, kAi = 3 • 10-9см3/с, аае(Е, p) = рАехр [—В (Е)], kPi =

(1.0 - 1.5) • 10-9 см3/с, ре = 5.4 • 10-27(Те)4-5 см6/с, Р'е=2.4 • 10-31Т(Те)-3'5 см6/с, k*,, =

• 7.3 • 10 ^-8 см³/с, k_Ai = 3 • 10 ^-9 см³/с, k _kon = 1.8 ^ 2,5 10-31 см⁶/с, у =0,1,

где p ‒ давление (торр); d ‒ межэлектродное расстояние (см); U ‒ приложенное напряжение (В), A=12 (см∙торр)^-1, B=180 (В/см∙торр); T ‒ температура газа (эВ); T e ‒ температура электронов (эВ).

Наиболее распространенным методом решения дифференциальных уравнений в настоящее время является метод прогонки сеточных уравнений, а с учетом постоянства для определенной итерации физических величин, определяющих состояние плазмы, можно применить метод Рунге‒Кутта.

Свойства низкотемпературной плазмы разрядов в газах повышенного давления при небольших значениях степени ионизации во многом определяются столкновениями электронов с атомами газа. Частоты упругих и неупругих столкновений при этом, как правило, превышают обратные времена других процессов, и, соответственно, именно эти столкновения опре- деляют вид функции распределения электронов по скоростям (в изотропном случае по энергиям (ФРЭЭ)). В свою очередь, вид ФРЭЭ определяет скорости процессов ионизации, диссоциации и, соответственно, компонентный состав плазмы и концентрации возбужденных атомов. Наиболее последовательный подход при решении указанной проблемы в условиях, когда можно пренебречь газодинамическими эффектами, а электрическое поле считать однородным, состоит в совместном решении кинетического уравнения Больцмана для ФРЭЭ и уравнений баланса для концентрации нейтральных, заряженных и возбужденных частиц. Совместное решение этих уравнений позволяет определить наиболее важные характеристики плазмы, такие как транспортные коэффициенты (электронная и ионная проводимость, теплопроводность), дрейфовую скорость Vdre, коэффициент диффузии De, среднюю характеристическую энергию электронов Te. Ввиду определенных ограничений по экспериментальным данным рассматривается методика нахождения константы возбуждения kst во всем межэлектродном промежутке. Рассмотрение кинетики электронного газа, а также уравнения баланса совместно с уравнением Больцмана и транспортными коэффициентами позволяет реализовать методику последовательного расчета динамики развития с учетом изменяющихся параметров плазмы.

Результаты расчетов

Расчеты проводились в аргоне для следующих экспериментальных условий: острие катода радиусом r=25 мкм; анод представляет собой диск диаметром D=11 см; межэлектродное расстояние d=4 см; прикладываемое напряжение U =3 кВ; давление атмосферное p=1 атм; расход газа G=10-5 кг/с. Радиус сечения разряда в области развития берется из экспериментальных данных по визуальным наблюдениям.

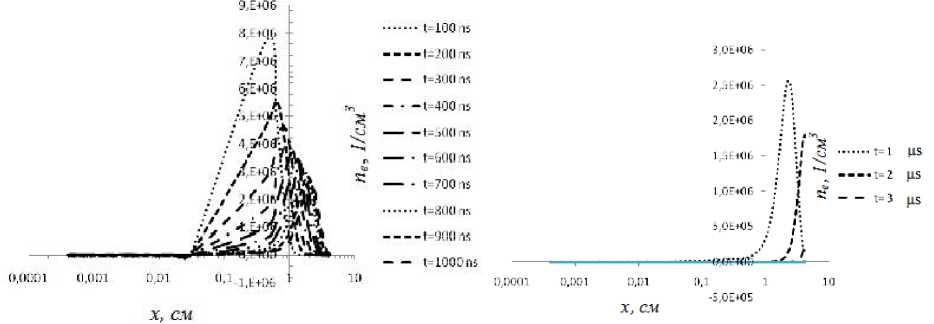
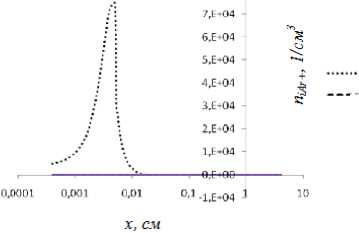
Увеличение концентрации электронов в прикатодной области обусловлено Таунсендов-ским механизмом размножения. Вследствие ионизации происходит увеличение количества электронов и ионов, а также молекулярных ионов в генерационной зоне, о чем свидетельствуют рисунки 1-3, на которых представлена динамика их концентрации вдоль оси острия катода в моменты времени 100÷1000 нс. Рост концентрации молекулярных ионов обусловлен реакцией конверсии и при ∼ 200 нс концентрация ионов Ar⁺ практически исчезает в прикатод-ной области, а также незначительное увеличение молекулярных ионов появляется за счет ассоциативной реакции метастабильных и возбужденных атомов. Волна ионизации в прикатод-ной области рождает возбужденные атомы и ионы. Следствием столкновения возбужденных и метастабильных атомов между собой и с нейтральными атомами генерирует молекулярные ионы, которые дрейфуют к катоду. Различие кривых концентраций молекулярных ионов и электронов объясняется отличием дрейфовых скоростей более чем на 10 порядков, и при временах достижения электронов поверхности анода, ионы, преодолевая генерационную зону достигают максимума непосредственно в прикатодной области. За счет роста молекулярных ионов в прикатодной области и непосредственного столкновения с катодом образуются вторичные электроны, что способствует дальнейшему развитию разряда. Концентрация положительных ионов Ar⁺ значительно снижается уже при 200 нс.

Молекулярные ионы Ar2+ только начинают расти, и максимум тока в импульсе соотносится ко времени максимальной концентрации молекулярных ионов на катоде (рис. 5 a). При этом максимум ионного тока и максимум напряженности поля, созданной пространственным положительным зарядом (рис. 4 b), сотносится ко времени этого процесса. При дрейфе молекулярных ионов к катоду за счет диссоциативной рекомбинации происходит гибель электронов в прикатодной области. Численное значение скоростей ионно-электронной эмиссии и рекомбинации молекулярных ионов с течением времени показаны на рисунке 5 b, и при условиях, указанных ранее, происходит пересечение этих кривых, а дальнейший рост скорости рекомбинации молекулярных ионов при условии уменьшения вторичных электронов приводит к нарушению условия самоподдержания, т.е. исчезновению вторичных электронов. По мнению некоторых ученых, именно данное обстоятельство приводит к появлению токовых импульсов. На рисунке 5 b наличие первого пика в графике скорости рекомбинации относится ко времени преобладания рекомбинации над скоростью вторичной эмиссии. Дальнейший рост скорости рекомбинации обусловлен дрейфовым продвижением молекулярных ионов к катоду, что на графике (рис. 5 b) выражено вторым пиком скорости рекомбинации.

I 41 ( V

I. LOODni

b

a

S.E-O4

t-100ns

—l-JOOn>

c

Рис. 1. Динамика развития концентрации электронов в разрядной области: a-100-1000 нс; b ‒ 1-3 мкс; с ‒ динамика развития концентрации ионов Ar ⁺ в разрядной области

a

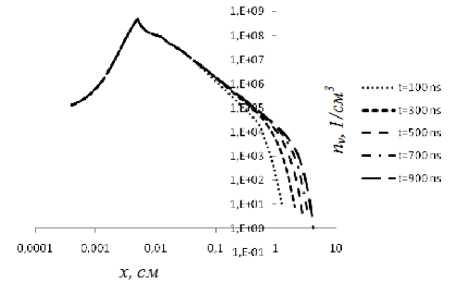
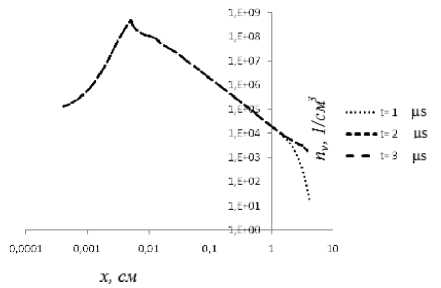
Рис. 2. Динамика развития концентрации метастабильных атомов в разрядной области: а ‒ 100-900 нс; b ‒ 1-3 мкс

b

На рисунке 4 а показана зависимость концентрации электронов в прикатодной области на участке времен от начала развития первой волны ионизации. Из графика видно, что значение ионной концентрации спадет уже при 200 нс, данный спад приводит к росту концентрации молекулярного иона. И дальнейший рост молекулярных ионов непосредственно в прикатод-ной области приводит к уменьшению электронов вплоть до их исчезновения при временах ∼200 нс от начала развития первой волны ионизации. При напряжении U=3 кВ на межэлектродном промежутке весь пространственный положительный заряд молекулярных ионов Ar2+ достигнет в прикатодной области (непосредственно вблизи поверхности катода) таких малых значений, что случайный электрон в генерационной зоне не начнет развитие новой волны ионизации. Такое предположение описывает развитие токовых импульсов на начальной стадии импульсно-периодического режима.

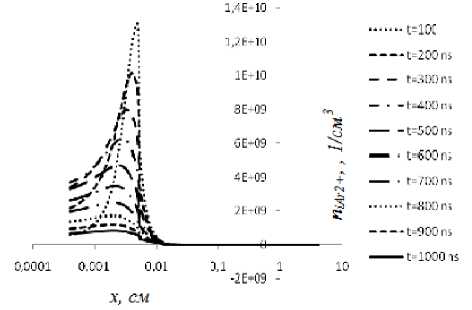
a

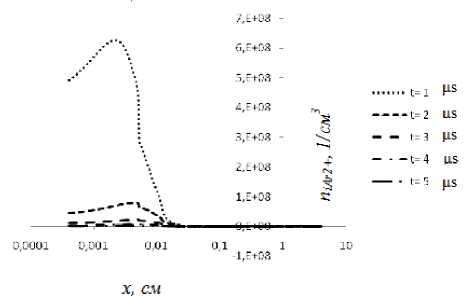
b

Рис. 3. Динамика развития концентрации молекулярных ионов Ar 2⁺ в разрядной области: а ‒ 100÷1000 нс; b ‒ 1-5 мкс

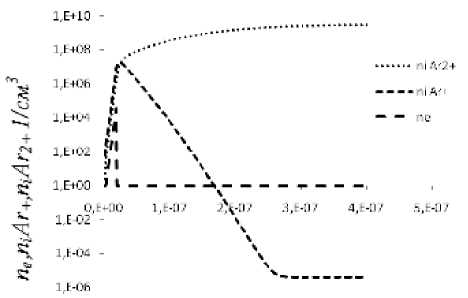
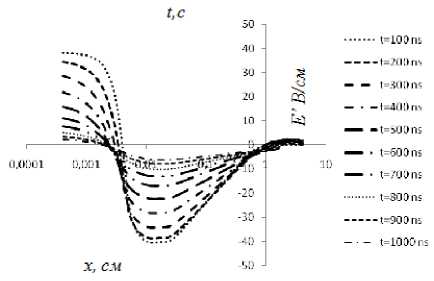
a                                             b

Рис. 4. а ‒ концентрация ионов Ar 2⁺ , Ar ⁺ и электронов на катоде; b ‒ напряженность поля в прикатодной области

Суммарный ток Io в межэлектродном промежутке рассматривается как сумма токов, ионного тока 1^, тока смещения Ismи электронного тока 1е (рис. 5 а). Из рисунка видно, что максимум ионного тока соотносится со временем максимальной концентрации молекулярных ионов, достигающих катода. Значительное снижение тока смещения происходит за счет дрейфа электронов с прикатодной области и резкого расширения области развития разряда в 1,5D мерной модели. Решение уравнения Пуассона в динамической модели представлено на рисунке 4 b в разные моменты временной итерации. Согласно рисунку, напряженность поля непосредственно в прикатодной области имеет положительное значение, а затем при дрейфе электронов пространственный заряд электронов создает отрицательную напряженность поля, уменьшающую приложенное поле. При 1,5 мкс достигает максимума электронный ток, при этом электронный ток определяет дополнительные выпуклости на задней части импульсов тока. Согласно работе [7] первый максимум тока связывают с током смещения, но в действительности за данный пик в токовом импульсе отвечает ионный ток непосредственно в прика-тодной области, образующийся вблизи катода, а следующая выпуклость определяется дрейфом положительных молекулярных ионов, образующихся на расстоянии 0,008 см от катода (максимум концентрации молекулярных ионов в межэлектродном пространстве при временах 100 нс достигается на расстоянии 0,008 см) (см. рис. 3 а). Анализ токов показывает, что в разрядном промежутке основной вклад в общий ток вносит ионный ток. Электронный ток не изменяется при достижении длительности импульсов порядка 10-4 с и не изменяется с течением времени. Численное значение электронного тока составляет порядка нескольких микроампер (рис. 5 a). Незначительный вклад тока смещения определяет разного рода изменения на форме импульсов. Длительность импульсов лежит в миллисекундном диапазоне. Характерное время

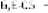
recombination

emission of electron

c

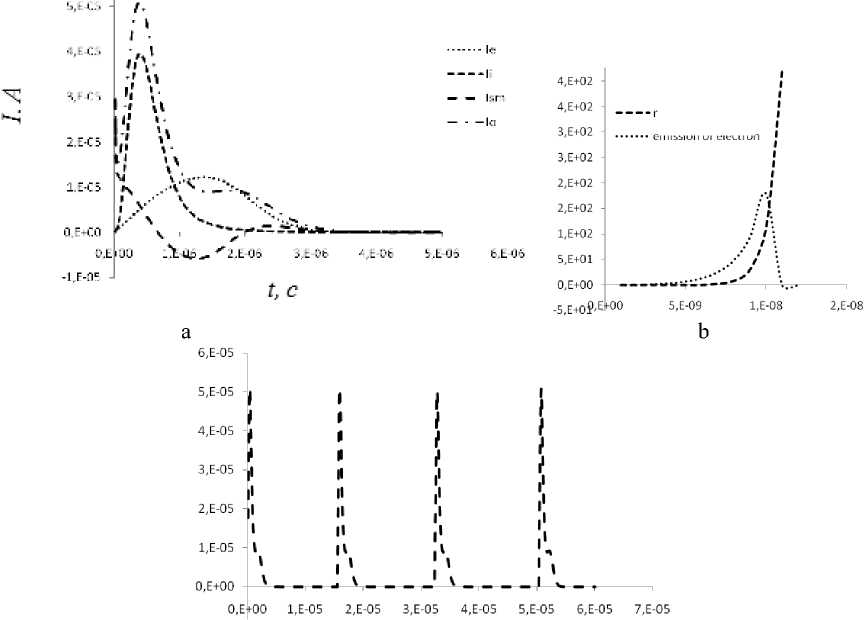
Рис. 5. а ‒ ионный ток Ii, ток смещения Ism, электронный ток Ie и полный ток Io в зависимости времени; b ‒ зависимость скорости рождения и гибели электронов непосредственно в прикатодной области от времени; с ‒ токовые импульсы данных процессов в молекулярных газах составляет порядка 10-6 с, что на два порядка превышает время нестационарных процессов в аргоне. Задержка по времени в длительности импульсов в аргоне при незначительном продуве разрядной области объясняется различием концентрации и дрейфовой скорости молекулярных ионов Ar2+, достигающих катода, соответствующих определенным условиям. Действительно, эксперименты показывают, что длительность импульсов зависит от разных факторов. При увеличении расхода газа длительность времени уменьшается, поэтому начало новой волны ионизации можно связать с выносом возбужденных и метастабильных атомов и молекулярных ионов с разрядной области, но за характерное время токовых импульсов никакого изменения концентрации возбужденных атомов, отвечающих за образование молекулярных ионов, не происходит (рис. 2 a, b). Но все же основным фактором изменения длительности импульсов является электрическое поле на разрядном промежутке, при увеличении которого растет дрейфовая скорость молекулярных ионов. И в отличие от молекулярного газа время восстановления условия развития новой волны ионизации в атомарном газе Ar лежит в миллисекундном диапазоне, что показано в расчетах, указанных на рисунке 5 c. Из рисунков видно, что амплитуда токовых импульсов не изменяется, при этом значение усредненного тока во времени растет за счет изменения длительности колебаний, что приводит к изменению вольтамперной характеристики. Влияние расхода газа на развитие и длительность импульсов тока требует дальнейших исследований.

Заключение

Численное моделирование развития разряда с учетом основных элементарных процессов, происходящих в неравновесной плазме, в атмосфере аргона показывает динамику развития токовых импульсов, длительность которых соответствуют по порядку величины с экспериментальными данными. Особенностью модели является учет изменения параметров плазмы на основе рассмотрения ФРЭЭ. Нарушением условия самоподдержания и появления импульсов тока является наличие молекулярных ионов Ar 2 ⁺, дрейфующих к катоду, и превышение скорости диссоциативной рекомбинации над вторичной эмиссией электронов.