Формирование классов объектов методом дискриминантного анализа

Дискриминантный анализ является статистическим методом, который позволяет изучать различия между двумя и более группами объектов по нескольким переменным одновременно и дает возможность классифицировать объекты по принципу максимального сходства.

Цель работы: рассмотреть классификационные различия между классами объектов и графически интерпретировать полученные результаты.

«Дискриминантный анализ» - это общий термин, относящийся к тесно связанным статистическим проц едурам: интерпретации и классификации. Интерпретация предполагает поиск различий между классами при данном наборе характеристик (переменных). Метод, относящийся к классификации, связан с получением одной или нескольких функций, обеспечивающих возможность отнести каждый объект к одной из групп [1].

В дискриминантом анализе используются методы максимального правдоподобия:

• 1)    расчет априорных вероятностей принадлежности к классу, которые можно рассматривать как решающее правило, применяемое в том случае, когда нет никакой дополнительной информации об объектах;

• 2)    расчет условных вероятностей принадлежности к классу, каждая из которых равна вероятности получить соответствующее значение дискриминантной функции при условии, что объект принадлежит классу.

Содержанием дискриминантного анализа является разработка и исследование статистических методов для изучения различий между двумя и более группами объектов по нескольким переменным одновременно при помощи дискриминантной линии.

В дискриминантном анализе, в отличие от кластерного, имеется обучающая выборка, в которой известно к каким классам относятся объекты. По обучающей выборке получают правила, которые в дальнейшем позволяют определить, к какому классу относятся новые объекты.

Функция с линейной комбинацией вида:

f km ^u 0 + ^u 1 X 1km + ^u 2 X 2km + • •••+ u p X pkm ,      ⁽¹⁾

где f_km - значение канонической дискриминантной функции для m-го объекта в группе k ; X_1km - значение дискриминантной переменной X i для m -го объекта в группе k ; u i - коэффициенты, обеспечивающие выполнение требуемых условий.

Коэффициенты ui для первой функции выбираются таким образом, чтобы ее средние значения для различных классов как можно больше отличались друг от друга. Коэффициенты второй функции выбираются так же, то есть соответствующие средние значения должны максимально отличаться по классам, при этом налагается условие, чтобы значения второй функции были некоррелированы со значениями первой.

При классификации указанный объект

«принадлежит к» или «очень похож на» данный класс. Такое решение принимается на основе информации, содержащейся в дискрими где Л - собственное значение; vt - последова-тельностькоэффициентов; wtj, btj - рассчитаны соотношениями (3) и (4) соответственно:

д ^к wtj = ^ ^ (Xtkm — ^ik)(Xjkm — Xjk), (3) k=1 т=1

btj = tij - wij■

• 2.    По проценту объясненной дисперсии:

• 3.    По расчету коэффициента канонической корреляции, который является мерой связи (степени зависимости между группами и дискриминантной функцией).

• 4.    По расчету Л - статистики Уилкса -меры различий между классами по н ескольким дискриминантным переменным:

Лобщ = Л1 + Л2 + - + Лп,(5)

Л1

й =      ■(6)

^Л общ

Процент объясненной дисперсии показывает, какова функция по сравнению с другими, то есть та, которая имеет большее процентное содержание, сильнее влияет на дискриминацию.

д

Л = П .' t=k+1 ^t

где k - число уже вычисленных функций; символ П означает, что для получения окончательного результата необходимо перемножить все члены. Л является «обратной» мерой, потому величины Л, близкие к нулю, говорят о высоком различении (то есть центроиды классов сильно отличаются друг от друга).

Каждый объект принадлежит одной из групп, поэтому вероятность принадлежности вычисляется для любой из групп. Вероятность того, что объект ^является членом класса k, равна:

p_r(С in - ^Pr™^Gk) rm ^k “L g= ₁Pr(x|C k )' ⁽⁾

где Pr(XiG k ) - вероятность того, что объект, находящийся далеко от центроида, действительно принадлежит классу k .

Стандартизованной мерой эффективности для любого количества классов является т- нантных переменных.

Значимость дискриминантной функции при классификации определяется несколькими способами:

статистика ошибок:

нс

-

I^Pi^t

Т п — Уд

11общ   Lt=1

P t ^ t

1. По расчету собственного значения функции:

, _ LbjVt

Л ул        '

LWt^t где т - число правильно классифицированных объектов; pt - априорная вероятность принадлежности к классу; а ig=1ptnt представляет собой число объектов, которые будут правильно предсказаны при случайной классификации.

Дискриминантные переменные - оси p -мерного евклидова пространства. Каждый объект описывается точкой этого пространства с координатами, представляющими собой наблюдаемые значения каждой переменной. Если классы отличаются друг от друга по наблюдаемым переменным, их можно представить как скопления точек в некоторых областях рассматриваемого пространства. Поскольку классы могут частично «перекрываться», соответствующие им «территории» не совпадают. Для определения положения класса вычисляется его «центроид» - точка, координаты которой есть средние значения переменных в данном классе.

Радиус ядра разброса наблюдений рассчитывается по формуле:

R t = f_t + V2 * a_t, (10) где r_t среднее расстояние между центром кластера и кластерными элементами, a a t среднеквадратическое отклонение величины.

В ходе выполнения работы была сформирована база данных, состоящая из 595 анализов, характеризующих качество муки по 15 признакам. Каждый анализ описывался химическими (массовая доля белка, массовая доля золы, массовая доля жира, содержание клетчатки и водорастворимых углеводов) и органолептическими показателями качества муки (влажность, титруемая и активная кислотность, массовая доля и качество клейковины, вкус, запах, хруст и т.д.). В соответствии с классификацией, предложенной в [3], наблюдения были разделены на 4 группы качества. Первая группа (класс 1 высшего качества) - 140 (23,3 %) наблюдений; вторая (класс 2 хорошего каче ства) - 195 (33,3 %); третья (класс 3 плохого качества) - 140 (23,3 %); четвертая (класс 4 очень плохого качества) - 120 (20,0 %).

Исходные качественные признаки были формализованы в категориальные. Качественный признак, например, «вкус», переведен к бинарному виду, где каждый признак имел 2 состояния ( 0 - признак отсутствует, 1 - присутствует): вкус свойственный ( 1 - присутствует, 0 - отсутствует); вкус заплесневелый ( 1 - присутствует, 0 - отсутствует); вкус затхлый ( 1 - присутствует, 0 - отсутствует); вкус кисловатый ( 1 - присутствует, 0 - отсутствует); горьковатый ( 1 - присутствует, 0 - отсутствует). Таким образом, количество признаков увеличилось до 25 [2].

Исходные данные представляют собой случайные величины. Полная информация о случайной величине дается ее функцией распределения. По критерию Колмогорова-Смирнова установлено, что для подавляющего большинства признаков распределение отличается от нормального на уровне значимости P=0,05. Нормальному закону распределения подчиняются признаки: газообразующая способность и содержание водорастворимых углеводов.

Для принятия решений об отнесении хлеба к определенному классу необходимо отобрать наиболее информативные признаки. Выявление наиболее информативных признаков и классификация осуществлялась в два этапа. На первом этапе использовался корреляционный анализ. На втором этапе формировалась классификационная система признаков методом дискриминантного анализа. Методика классификации методом дискриминантного анализа представлена на рисунке 1.

Сбор экспериментальных данных за период времениt

Матрица исходных-дан.-ных

Получение классов экспертным путем

Построение групп классов объектов

Рисунок 1. Методика классификации методом дискриминантного анализа

В качестве критерия информативности признаков принят коэффициент корреляции между признаком и классом качества муки, определенным экспертом.

Для первого класса были выявлены 2 специфических признака: цвет муки белый Хю и содержание водорастворимых углеводов Х₂₈, коэффициент корреляции которых варьируется от 0,755 до 0,819, то есть теснота связи сильная. Для 6 признаков (титруемая кислотность Х₂, активная кислотность Х₃, массовая доля клейковины Х 4 , число падения Х₇, цвет муки Х₈, белизна Х₂₆, зольность Х₂₇) значение коэффициента корреляции превышает 0,5 по модулю, то есть теснота связи средняя.

Для второго класса выявлен 1 специфический признак: цвет муки с желтоватым оттенком Х12, коэффициент корреляции которого 0,826, то есть теснота связи сильная. Для 3 признаков (вкус свойственный Х14, отсутствие затхлого вкуса Х18, запах свойственный Х19, отсутствие хруста Х23) коэффициент корреляции находится в диапазоне от 0,508 до 0,655 по модулю, то есть теснота связи средняя.

Установлено, что третий класс имеет 1 специфический признак: цвет муки серый Хц, значение r равно 0,748. Для 4 признаков: вкус несвойственный Х₁₄, вкус кислый Х₁₅, вкус затхлый Х₁₈, запах несвойственный Х₁₉, значение коэффициента корреляции варьируется от 0,550 до 0,691, то есть теснота связи средняя.

Для четвертого класса было получено 7 специфических признаков: титруемая кислотность Х₂, массовая доля клейковины Х 4 , число падения Х₇, крупность помола Х₉, вкус плесневелый Х₁₇, зольность Х₂₇, коэффициент корреляции которых лежит в диапазоне от 0,717

до 0,952. Для 9 признаков (активная кислотность Х2, цвет серый с частицами Х13, вкус несвойственный Х14, вкус плесневелый Х17, активная кислотность Х3, запах с посторонними примесями Х22, наличие хруста Х23, наличие металлопримесей Х25, белизна Х26, содержание водорастворимых углеводов Х32, коэффициент корреляции находится в диапазоне от 0,563 до 0,656 по модулю и имеется средняя теснота связи с классом качества.

Для повышения точности классификации был использован метод дискриминации. Преимуществом данного метода является автоматическое построение графиков распределения классов и функций дискриминации.

Была сформирована обучающая выборка из 50 (8,4 % ) наблюдений, содержащая объекты всех классов муки. Также как и для кластерного анализа были приняты признаки, отобранные на первом этапе методом корреляционного анализа, имеющие значимую корреляцию с классом качества. Классификационная система признаков включает в себя: цвет муки белый X₁₀ , цвет муки серый X 11 , цвет муки с желтоватым оттенком X₁₂, вкус плесневелый X₁₇, титруемая кислотность X₂, массовая доля клейковины X 4 , число падения X₇, цвет муки X₈, крупность помола X₉, зольность X₂₇, содержание водорастворимых углеводов X₂₈.

Полезность дискриминантной функции оценивалась при помощи расчета коэффициента канонической корреляции (3); различие между классами - с помощью Х-статистики Уилкса (4); значимость дискриминантных функций - с помощью распределения х2 (хи-квадрат). Результат дискриминантного анализа представлен в таблице 1.

Таблица 1

Результат дискриминантного анализа

Функция	Собственное значение	% объясненной дисперсии	Кумулятивный %	Каноническая корреляция	Лямбда Уилкса	Хи-квадрат
D1	5901,95	98,4	98,4	1,000	0,000	9118,57
D2	83,95	1,4	99,8	0,994	0,001	4051,92
D3	11,208	0,2	100,0	0,958	0,082	1459,97

Функция D1 обладает большими дискриминирующими возможностями, так как ее собственное значение равно 5901,95. Процент объясненной дисперсии 98,4 %, значение канонической корреляции 1,0 и распределение х2 9118,57 подтверждает дискриминационные возможности функции D1. Так как значения функций D2 и D3 по данным критериям несколько ниже, данные функции не сильно влияют на процесс дискриминации.

Канонические дискриминантные функции D1, D2, D3, разделяющие выборку на 4 класса:

D1=-163,01-0,2Х 2 +0,01Х₄-0,01Х 7 +0,01 Х 9 -0,56Х 12 +0,27Х 15 -0,3Х 16 -0,07Х 17 -0,4Х 20 -0,41Х 22 +223,14Х 25 ;

D2=-6,17+0,3X 2 -0,01X+0,03X 7 -0,01X 9 +0,17X 12 -4,1X 15 +1,05X 16 -0,84X 17 +0,59X 20 -0,2X 22 +1X 25 ;     (12)

03=12,61-2,01x 2 -0,561x 4 -0,027x 7 -0,026X 9 +2,21x 12 +2,48X 15 +5,33x 16 +2,33x 17 +1,18X 20 +          (13)

+1,46X 22 +3,275X 25 .

Уравнения линейных простых класси-      позволяющие относить объекты к одному из 4

фицирующих функций D1k, D2k, D3k, D4k,      классовкачества:

D1k=-3346,35+85,73X2+48,19X4+2,29X7+1,57X9-31,29X12+115,86X15+28,91X16+29,21X17--60,80X20+70,56X22+13936,45X25;

D2k=-5034,72+77,66X 2 +44,98X 4 +1,99X 7 +1 ,44X 9 -31,74X 12 +137,58X 15 +59,14X 16 +41,51 Х 17 --63,9X 20 +69,42X 22 +47887,02X 25 ;

D3k=-39368,68+115,34X2+47,81X4+1,074X7+1,71X9-144,32X12+164,55X15-15,2X16+ +18,39X17-143,9X20-13,02X22+155295,13X25;

D4k=-39421,92+113,14X 2 +47,94X 4 +0,79X 7 +1,72X 9 - 146,33X 12 +201,51 Х 15 -25,4Х 16 +25,79Х_П--149,62X 20 -11,99X 22 +155276,21 Х 25 .

Первые две наиболее дискриминирующие канонические дискриминантные функции и центры в классах качества представлены на рисунке 2. Центроиды четырех классов имеют следующие координаты: (-68,74; 14,46; -0,11), (-66,85; -10,51; 0,05), (86,59; 0,33; 4,62), (87,81; -0,18;-5,43).

Рисунок 2 показывает, что группы 1 и 2 вполне различимы, то есть центроиды хорошо отделимы друг от друга. На рисунке четко видно попадание одного ошибочно отнесенного наблюдения второго класса к первому. Однако выявлено перекрытие областей между 3 и 4 классами качества. Это обусловлено тем, что значения дискриминантных функций в центроидах групп для 3 и 4 классов близки друг к другу: 86,59 и 87,81 соответственно.

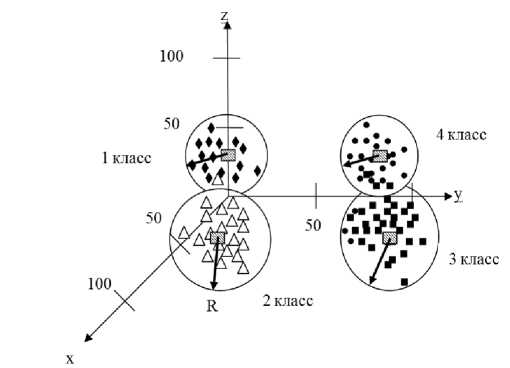
Рисунок 2. Канонические дискриминантные функции для четырех классов качества и центры групп

Результаты классификации методом дискриминантного анализа представлены в таблице 2.

Таблица2

Результат классификации

Категория класса качества		Предсказанная принадлежность к группе				Итого
		1	2	3	4
cd Н О н о cd	1 класс	140	0	0	0
	2 класс	1	194	0	0
	3 класс	0	0	137	3
	4 класс	0	0	3	117
%	1 класс	100	0	0	0
	2 класс	0,5	99,5	0	0,0
	3 класс	0,0	0	97,2	2,8
	4 класс	0,0	0,0	1,7	98,3	100,0

С учетом изложенного, по результатам расчета методом дискриминантного анализа выявлено, что число случаев ложной тревоги составило 3 (2,8 %) - это отнесение плохого качества к худшему. Выявлено 4 (2,3 %) случая пропуска сигнала, из них в 1 (0,5 %) наблюдении хорошее качество было неверно классифицировано как очень хорошее качество, в 3 (1,7 %) других случаях очень плохое качество расценено как плохое качество. По результатам дискриминации было выявлено, что в первом классе было верно классифицировано 140 (100,0 %) наблюдений, во втором классе -194 (99,5 %), в третьем - 137 (97,2 %), в четвертом - 117 (98,3 %). Таким образом, точность классификации методом дискриминантного анализа составила 576 (98,02 %). При этом ошибки отнесения плохого качества к очень плохому не стоит принимать во внимание, так как мука и плохого и очень плохого качества не должна использоваться в хлебопечении.

ВестникВГУИТ, №1, 2014