Формирование компетентности проведения вычислительного эксперимента у студентов математического профиля

Современные государственные требования [3] к выпускнику вуза предполагают повсеместное привлечение студентов к активной самостоятельной работе, направленной на формирование компетентностей (развитие знаний, умений, навыков) по профилю подготовки, которые в свою очередь формируют компетентность выпускника в конкретной области. Данная статья посвящена проблеме формирования компетентности проведения вычислительного эксперимента у студентов математического профиля как одной из форм реализации компетентностного подхода в условиях высшего профессионального образования. При этом необходимо уделять повышенное внимание организации самостоятельной работы студентов. Целями самостоятельной работы как важнейшей составляющей учебного процесса по подготовке высококвалифицированных специалистов являются закрепление, расширение и углубление теоретических и практических знаний, полученных студентами в процессе теоретического обучения. При планировании самостоятельной работы следует учитывать то, что эта работа должна быть направлена не только на подготовку компетентного в данной дисциплине специалиста, но и на развитие компетентностей в деятельности междисциплинарного характера, служащих основой для формирования высококвалифицированного специалиста по математическому направлению. Одним из аспектов работы в этом случае является организация и проведение эксперимента, который позволяет развивать исследовательские навыки и, кроме того, формировать базу для послевузовского образования, в том числе и педагогического [1].

При планировании самостоятельной работы студентов, как пропедевтики вычислительного эксперимента, необходимо учитывать следующее: самостоятельная работа играет важнейшую роль в развитии логического мышления, способности аргументированно рассуждать. Например, бакалавры направления «Педагогическое образование» должны обладать общекультурными компетенциями 1, 6 (расшифровку компетенций можно посмотреть в [3]); содержание самостоятельной работы студента естественным образом должно имитировать интеллектуальные действия и исследовательские навыки (отвечает специальным компетенциям, определяемым вузом).

Самостоятельная работа студентов может включать:

• -    изучение лекций, обязательной или дополнительной литературы и иных источников по данной теме;

• -    решение предложенных преподавателем задач;

• -    составление задач по данной теме;

• -    поиск решения задач, если схема рассуждения еще не известна;

• -    поиск алгоритмов составления и решения задач определенного типа;

• -    анализ задач, составленных сокурсниками, выявление и исправление в них недочетов, решение этих задач (отвечает общепрофессиональным компетенциям 3, 4, профессиональным компетенциям 4, 9).

Рассмотрим формирование математической компетентности на примере формирования компетентности проведения вычислительного эксперимента у студентов математического профиля. Существуют различные точки зрения на определение математической компетентности. Мы понимаем ее как целостное образование личности, отражающее готовность к изучению математических дисциплин, способность использовать свои математические знания для разрешения различного рода практических и теоретических проблем и задач. Формирование компетент-

ности проведения вычислительного эксперимента у студентов будем рассматривать как процесс приобретения и становления компонентов математической компетентности, который характеризуется способностью опытным путем решать теоретические и практические задачи.

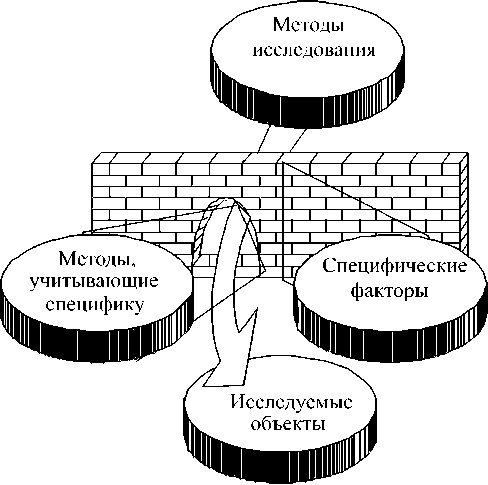
Рис. 1. Ситуация, возникающая при проведении эксперимента

В рамках вышесказанного рассмотрим организацию вычислительного эксперимента на примере применения математических методов для исследования химических структур (ХС). Для данной области традиционно использование наряду с химическими математических методов [4; 5]: довольно активно применяются методы математической статистики, регрессионного анализа, дифференциальных уравнений, нечеткой математики и т.д. При реализации предлагаемых подходов, конечно, необходимо учитывать квалификацию аудитории и в зависимости от этого предлагать соответствующую часть вычислительного эксперимента в виде готового решения.

При подготовке эксперимента необходимо обратить внимание на специфику методов исследования и предметной области (рис. 1). При анализе исходной информации следует учитывать ее природу, а при выборе формального представления также ориентироваться на предполагаемые методы исследования. Так, если исследования касаются идентификации веществ, то формулы химических соединений целесообразно будет представить в виде раскрашенных графов, а для экспертной оценки тех же ве- ществ подойдет другая форма – параметризация свойств вещества и построение метрического пространства.

Как правило, далее необходимо согласовать по формальному представлению исходные данные и методы исследования. Но и здесь могут возникать различные специфические факторы, касающиеся особенностей конкретной задачи. В нашем случае для ХС характерно возникновение различного вида неопределенностей, касающихся, например, качественных или приближенных оценок (см. рис. 2).

В этом случае может помочь аппарат нечеткой математики [2], общую схему применения которого можно изобразить в виде рис. 3. Такая подготовка данных позволяет ликвидировать неопределенности (тем не менее, сохраняя эти данные) и приводит все данные к одной размерности, что уже позволяет использовать широкий спектр математических методов, не оглядываясь на физико-химический смысл исходных параметров. А к природе результата можно вернуться потом, при его интерпретации.

Из рис. 2 также видно, что специфические факторы необходимо учитывать на протяжении всего исследования и постоянно возвращаться к проблеме того формального представления данных, которое в наибольшей степени удовлетворяет требованиям метода исследования. Сами методы, используемые при типичных операциях с ХС, обозначены на рис. 4.

Здесь необходимо также учитывать квалификацию аудитории и не проводить совместно весь комплекс исследований, а, выделив фрагменты и разделив их между студентами, организовать интерактивную работу. При этом естественно возникнет сотрудничество студентов, согласованность их исследований и обмен информацией, что повышает их компетентность в рассматриваемых вопросах и полностью соотносится с новыми стандартами [3].

Проявить компетентность студент может в случае применения знаний и умений при решении задач, отличных от тех, в которых эти знания усваивались. Для этого и необходим вычислительный эксперимент, позволяющий оценить работу студента. Диагностическими показателями и критериями сформированно-сти компетентности являются степень полноты выполнения программы, овладение основными вычислительными навыками, анализ выполненной работы, содержание и качество

Формирование базы данных

Сбор информации	Верификация	Классификация	Наполнение
Ошибочные и ! ПСЧСТКИС МИОПИЯ ; специалистов [	। Зашумленность, । информации ]	1 Разнородность 1 1 информации 1 [ Разнотипность [ [ информации [ । Неполнота , i информации ]	' Технические [ ошибки

	Анализ и синтез:
	Экспертиза	Прогноз	Конструирование
	Нечеткие мнения । специалистов । Разнородность [ информации 1	। Стати сти ческая 1 1 неопределенность,1 I случайность ।	। Статистическая । неопределенность, । случайность

Р азнот инность информации

Рис. 2. Специфические факторы, затрудняющие исследование ХС

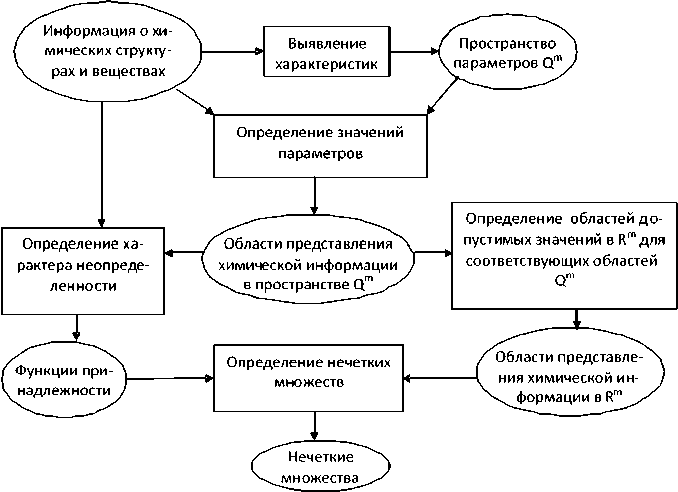
Рис. 3. Методы формализации данных (учитывающие специфику задачи)

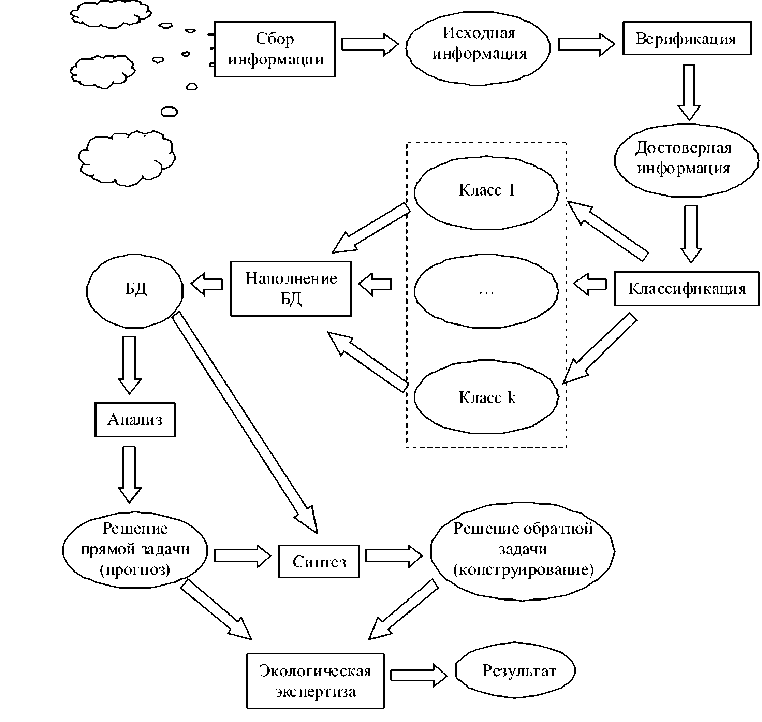
Рис. 4. Исследование ХС

оформления работы и ответы студента на задаваемые вопросы.

Поскольку компетентность представляет собой многоаспектную характеристику студента, касающуюся его профессиональных знаний и умений, практической подготовленности, творческих и личностных качеств, то необходимо оценивать сформированность компетентности. Наиболее объективным инструментом служит критериально-рейтинговая система качественной и количественной оценки уровня развития компетентности.

Таким образом, в данной работе рассмотрена проблема формирования математической компетентности при самостоятельной работе на примере формирования компетентности проведения вычислительного эксперимента у студентов математического профиля, указаны формируемые компетенции, оценка которых дает представление о сформированно-сти компетентности в указанной области.