Формирование математической модели механизма привода утюга на базе удельных действий

Расфасовочно-упаковочное оборудование следует отнести к классу машин, предназначенных для преодоления технологических сопротивлений при перемещении рабочего органа с требуемой скоростью [3].

Функцией цели такого класса машин является совершение механической работы силой mW на перемещение S . При этом ключевым удельным действием принимается удельное действие по Кориолису-Понселе, которое оценивает затраты механической работы при перемещении рабочего органа с заданной скоростью.

Для осуществления динамического анализа необходимо вычислить все удельные действия [2], которые определяют затраты механических средств. При этом необходимо осуществить разбивку рассматриваемого механизма по его узлам, а именно: привод, кулачок, коромысло, тяга, цепь, звездочка, утюг и пружина. Приоритетом при оценке закономерностей изменения удельных действий будет являться ключевое удельное действию по Кориолису-Понселе [1, 4]. Проведем формирование функций принуждения следующих удельных действий.

Удельное действие по Гауссу

Данное удельное действие оценивает конструкции связей (шарниров, стержней), структуру и износостойкость механической системы.

При определении величины данного удельного действия К_Гс в качестве подынтегральной функции используется функция принуждения Z_i механизма привода утюга

n

z = £z,

i = 1

где Z_i – функция принуждения рассматриваемого i-го звена.

Сформируем выражения принуждения для всех звеньев механизма.

Представим систему, состоящую из ротора электродвигателя и шкива, насаженного на вал ротора, в виде однородного диска (рис.1). Радиус диска равен Rср. р

R р + R ш

, а масса, приходящаяся на единицу

m р + тш площади, равна // = —---— nRcp. р

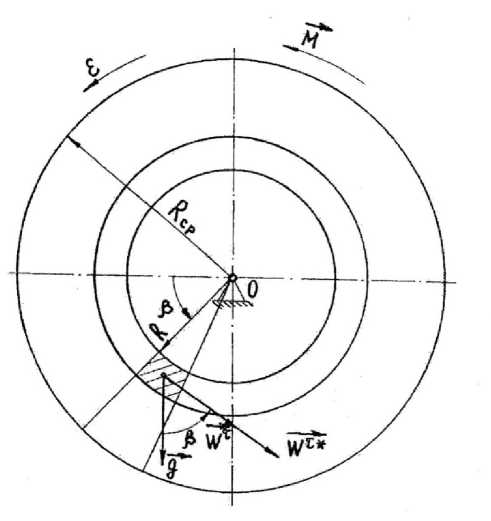
Рис. 1. Схема для определения функции принуждения однородного диска

Для данного условного диска элементарное принуждение равно [2]

d Z пр = 2 ( w * - W ) 2 dm ,

где W – действительное ускорение произвольной точки диска, м/с²;

W * - воображаемое по Гауссу ускорение произвольной точки диска, м/с²;

dr dm = ur--масса элементарной части диска, кг.

d p

Воображаемое ускорение произвольной точки тела по Гауссу представляет собой такое ускорение, которое имела бы точку, двигаясь под действием тех же активных сил, если бы с этого момента были установлены наложенные на нее связи [2].

Действительное ускорение произвольной точки диска

---    ---n *    

W = W + W , где Wn = юр2r, Wт = sрr - нормальная и тангенциальная составляющие ускорения, м/с2.

Воображаемое по Гауссу ускорение произвольной точки диска

W * = g + wn * + Wт*,(4)

где g – ускорение свободного падения, м/с² ;

Wn* = сар2r, W = —— r - нормальная и тангенциальная составляющие воображаемого уско-р            Jр рения, м/с² ;

М_{кр р} — крутящий момент на валу электродвигателя, Нм;

J_Р – момент инерции ротора, кгм².

Произведя соответствующие преобразования, получим выражение функции принуждения привода:

п   2( Мкр■ р\2

Rср■р '           s

J

Z пр = 1,85  f dZ= -у< m р + m,) х{ g2 +--------2-------},

^{( m} р ⁺ m , )

где 1,85 – коэффициент, учитывающий принуждение передаточных механизмов (от электродвигателя до приводной звездочки, расположенной на валу кулачка).

Принимая во внимание рассуждения, приведенные для привода, функциюпринуждения кулачка можно записать в виде

^{2 s} кул )

----------},

где m _кул , m _зв , m _ступ – масса кулачка, приводной звездочки и ступицы, на которую насажены кулачок и звездочка соответственно, кг;

R cp.y = 3 ^{( R} _K yл + R 3B^K + R myn ) ^- сРеДний РаДиУс,

М _{кр . кул} – крутящий момент на валу кулачка, Нм;

J _кул – момент инерции кулачка, кгм² .

Используя данную методику, определим функции принуждения для всех узлов, входящих в машину.

Для механизма коромысла, исходя из условия о том, что механизм коромысла принимаем за однородный прямолинейный тонкий стержень, (схема для вычисления его принуждения приведена на рис. 2), функция принуждения коромысла (после соответствующих преобразований) будет иметь вид:

1           da^ 2r 2  1 d a\2 2      da                d a zкор = 2m_ {g +(^) A, I. + 3(^) I. -2g(^) 2,lк sina+g-t,i, cosa}.     (7)

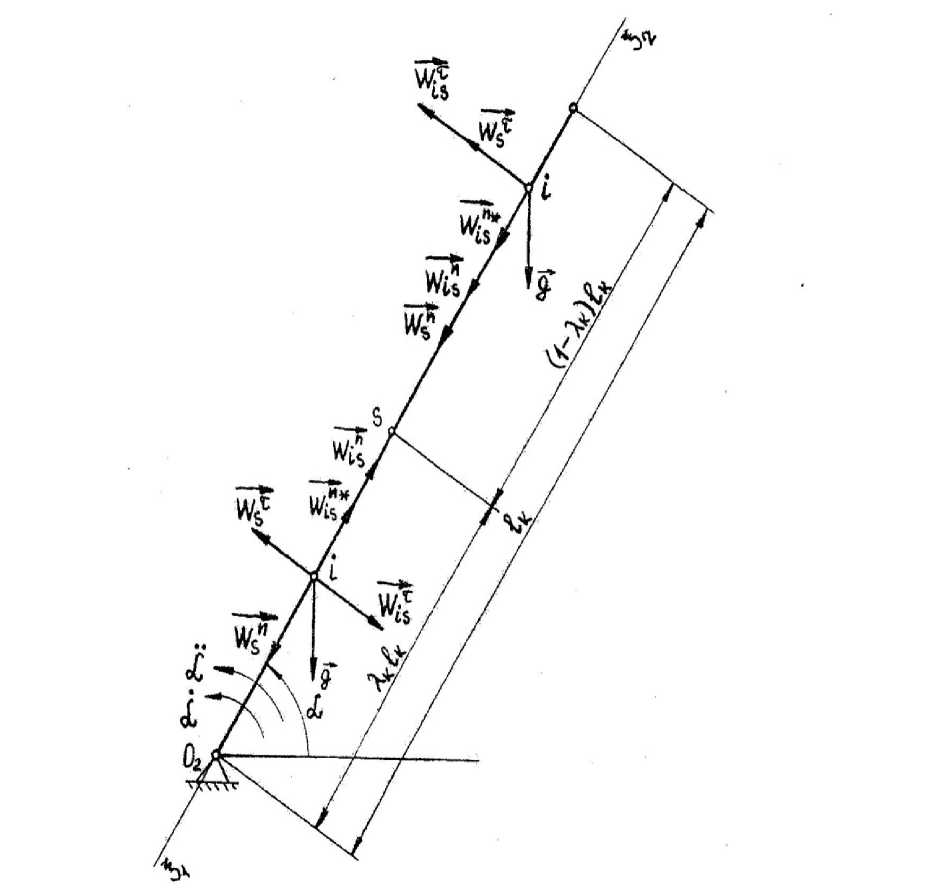
Рис. 2. Схема для определения функции принуждения коромысла

Для определения функции принуждения тяги (механизм которого рассматриваем так же, как прямолинейный тонкий стержень с центром масс в точке S (рис. 3)), вычислим действительное ускорение произ- вольной точки тяги. На основании этого, произведя необходимые преобразования, получим функцию принуждения тяги.

1      2 dα 4 2   d 2α 2 2   dβ 4 2 2

Ζ _Т =   m_Т { g + (   ) l_к + ( ₂ ) l_к + (   ) λ _Т l_Т - 2 g (   ) l_к sin

2           dt         dt          dtdt d 2α            dβ 2           dα 2 dβ 2

+ 2g     l cosα- -2g(   )2l λ sinβ-2(   )2l (   )2λ l cos(β-α) + dt2 к                 dt Т Т             dt к dt Т Т(8)

d 2α  dβ                 1 d 2 β 2   d 2 β

+2   2 lк(   )2λТlТ sin(β-α) + + ( 2 )2lТ2 +g 2 lТcosβ-()

dt2 к         ТТ                        2 Т         2 Тк

• 2 dt                        3 dt 2            dt 2

• d2β            d2α

×    ₂ l_Т sin( β - α ) -    ₂ l_{к   2} l_Т cos( β - α )}.

dt                 dtdt

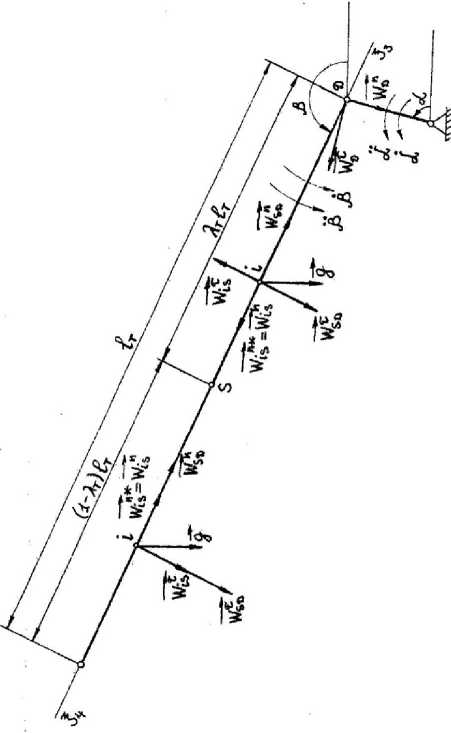
Рис. 3. Схема для определения функции принуждения тяги

Принуждение цепи складывается из принуждения трех участков цепи: участок присоединения к тяге, участок цепи, расположенный на звездочке, и участок присоединения к утюгу (рис. 4).

Ζц = ΖцТ + ΖцЗВ + ΖцУ.

Рассматривая цепь, присоединенную к тяге, как ее продолжение, получим принуждение этого участка цепи:

• 1      ¹ ит    2 da., 4 2 d a. 2 2     dp. 4                2 d в. 2

^Z uT = 7 mu "T^{ g +     ) lK + ⁽~aT ) ¹ к + (~77) ⁽ lT + ^ иТluT ) + (^rd) ^{[ 1} T ^{( 1} T + luT ) +

• 2    /         dt          dt           dtdt

ц

• 1   2 da,               da.             d a

+ -Т_цт ] - ² g (— ) ¹ к sin ^a + ² g (— ) ¹ sin ^a + ² g^Tl K ^{cos a} - ² g(-Г) ⁽ l T + l uT ^ uT ^{)sin в} -

• 3            dt                 dt                dtdt

  
  

• - 2(—) ² 1 ( d £ ) ² ( 1_T + A_TL _r)cos( в - a ) + 2 d -^ ( ^p ) ² ( 1 + _Л I _m)sln( p - a ) +

dt (it            uT uT                     dt2      dt            uT цт d 2 в           d 2 в           da 2 d 2 в              da 2 d 2 в

+ 2g—5“1 cos в + + g—1-1 cos p - 2(   )21 —sin(p - a) - (   )21K " —1-1 x цТ                       к        Т                            к          цТ dt               dt                dt dt                   dt dt x sln(p - a) - 2 d^-1 к d^- 1t cos(p - a) - - d^- i     1uT cos(p - a)}■

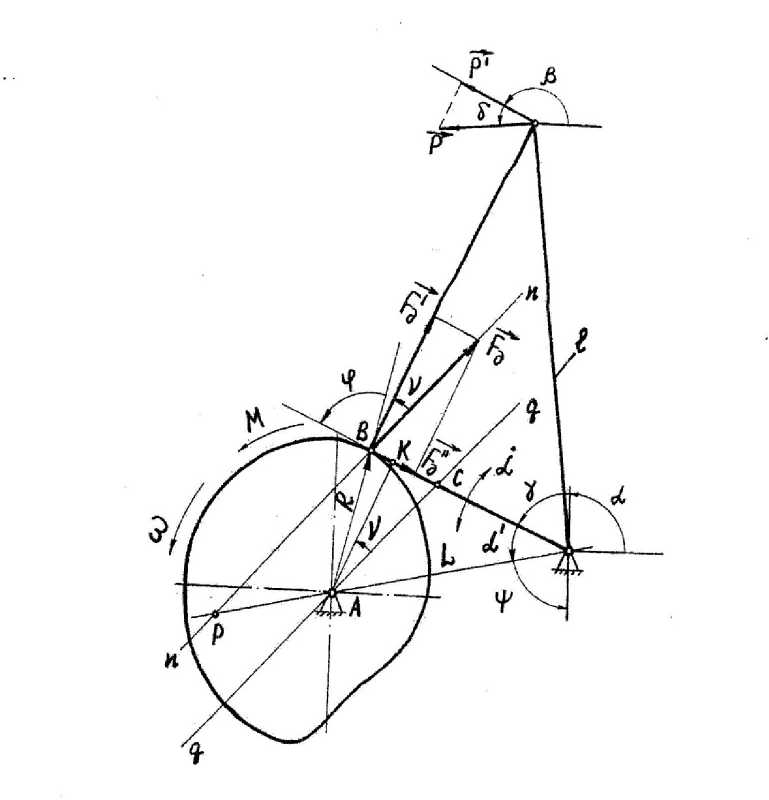
Рис. 4. Схема для определения силы, действующей на звездочку

Определив крутящий момент на звездочке, произведя при этом соответствующие преобразования, определим принуждение участка цепи, находящегося на звездочке (рассматриваем его как часть обруча (рис. 5)). Значение функции принуждение этого участка цепи будет иметь вид

¹       u^e               2 / крзв

^Z u3. = m^m₄ ~^{ g + ^R e_e ⁽~--

^{2       1} u                   J uee

-

4 gR. ( MM "р"

* 3. )² +-----------'

- * зв )

u . зв

π

},

где    1_цзв = ~R_3B — длина цепи, находящейся на звездочке, м;

М _крзв – крутящий момент на звездочке, Нм;

J_цзв – момент инерции цепи за звездочке, кгм²;

£ _зв - угловое ускорение звездочки, с .

Принуждение участка цепи, присоединенного к утюгу,

1    H_u   ,     d ² H_u   d ² H_u ,

Z = _ m —ц_ {g2 + 2 g----ц- + (----ц- )2} цу 2 ц I {S § dt2     d dt2    1'

ц

Подставив формулы (10) в (11) получим выражение принуждения всей цепи.

Принуждение звездочки вычисляется по формуле (1).

M

Z з 2 = - т зв { g ² + - R 3B ²(  ^ - ■ )²},

2         2 J ^

где    m_зв – масса звездочки, кг;

J _зв – момент инерции звездочки, кгм².

Принуждения утюга и пружины вычисляются также по формуле (1).

1      ,      d² H_u   d ² H ,

^Z у = 2 m у ^{ g ^{2 + 2} g d ^{+ (} dt ^)2};

7 _ 1

Z ППХЖ — m пруж

d 2H      2111

,       2 d Нружруж     d ^H пруж 2

пруж ^{{ g     g} dt ²      ( dt ²   ) ’

где

m _у , т_пруж — масса утюга и пружин соответственно, кг;

d H пруж d F

ускорение пружины, м/с².

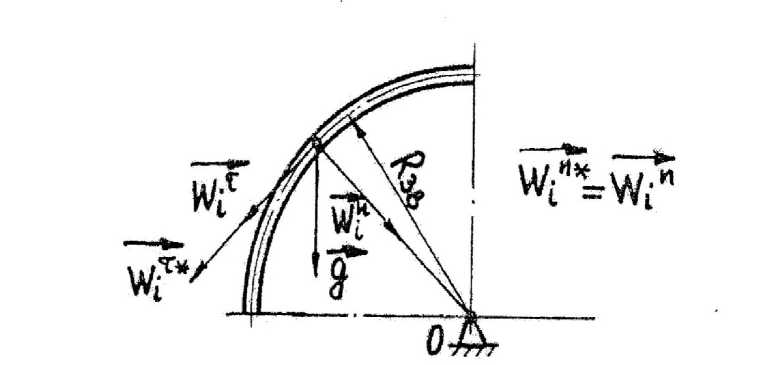
Рис. 5. Схема для определения функции принуждения участка цепи, расположенного на звездочке

Подставляя формулы (5)–(11) в формулу (1), получаем функцию принуждения системы, которая является только функцией времени t . Проинтегрировав данную функцию по времени, получаем величину удельного действия по Гауссу К_Гс .

Удельное действие по Аппелю

Удельное действие по Аппелю К_А оценивает действие сил инерции, т.е. характеризует напряженность динамического режима системы. В качестве подынтегральной функции используем функцию энергии ускорений V механизма (рис. 6).

n

V = z V i .

i = 1

-       ,,,2

где V i = —m i W i - энергия ускорений i - го звена.

Энергия ускорений привода, кулачка, коромысла, участка цепи, расположенного на звездочке, и звездочки вычисляется по формуле

V i = ¹ J,{( d^z ) 2 + ( d^- )⁴}.                                (16)

2 dt dt где Ji – момент инерции рассматриваемого звена механизма, кгм;

d Z d -

,     — угловая скорость и ускорение этого звена, с , с ².

dt   dt ²

Энергия ускорения тяги и участка цепи, присоединенного к тяге, вычисляется по формуле

V i = ^-[ mW ² + J i {(^ ) 2 + ( 'в)⁴}].                    (17)

2               dt dt где mi, Ji - масса и момент инерции рассматриваемого звена, кг и кгм;

W_iS – ускорение центра масс этого звена, м/с².

Энергия ускорений участка цепи, присоединенного к утюгу, утюга и пружины вычисляются по формуле v 1

V = —mi i 2

( dH

\2

< dt² ,

,

где m_i – масса рассматриваемого звена, кг.

Подставив в характеристики звеньев механизма соответствующие выражения и произведя преобразования, получим выражения энергии ускорений соответствующих механизмов звеньев:

для привода

	V np = 2 J ап ( ^ р 2 + ® р4 'ж ;                              (19)
для кулачка	V. = 1 J к,: f 2 + ® 4 )                             (20)
для коромысла	d a 2 ( — 4 4? кор 2 J кор {( dt 2)    ( dt } }’                                       ( )

1/   г?2₍ z da₂ d a 1,2₍ d ² в гвх^

VN = -(m> [lK {(—)2 + (—)4} + ~2T {(-тг)2 + On-2          dt dt 4 dt dt x da2 ^P^ d2в         d2a d2в для тяги - lKlT cos(P - a) xx[(—)2{(—)2 + —tgtg(в - a)] + —. {—y-) - (18)

к ^Т                   dt dt dt²                 dt ² dt²

- (dr)2 tg(в - a)}) + JT {(dd^)2 + (de)4}; dt                      dt dt для цепи

• ¹    <     ¹       1 d<^{a a},d^a d ¹      ,  «2 r/ ^d dfix^t

• V. = y! ^m .'2 ^{( l} K^r) ⁺ Hr) ⁺ 7< ^l + ^l >  ^{x [}<7Т) ⁺ Ф ^{] -}

• ^2       l                  ^dt            ^dt        4                       ^dt            ^dt

ц

7     7 X        X d da2r гв dP          da d2 в

^{- 1} к ^{( l} T + ^l .T ^{)cos( e - a} ) ^{xx {(}—) ^[(-77T ⁺ ~rtg ^{( в - a )] +} “ТТН— dt    dt )     dt               dt dt

-

для звездочки

( ^в tg ( P - a )]}) + J ( z ² + a *)}; dt

v3e =1J e(ze 2 + a2);

зв          зв зв зв

для утюга

1      d² H_u ,

V = Lm ( .- )²; у 2 dt^{2 j} ’

для пружины

1 d²H

V - 1m ( ---^A².

пруж 6 *пууж\ dt 2    '

Подставив формулы (21)–(25) в формулу (15), получим функцию энергии ускорений механизма, а затем и удельное действие по Аппелю.

Удельное действие по Лагранжу

Удельное действие по Лагранжу определяет затраты кинетической энергии-времени, действие масс элементов системы, взвешенное по квадратам их скоростей. В качестве подынтегральной функции используется кинетическая энергия Т механизма.

Удельное действие по Эйлеру

Удельное действие по Эйлеру К_Э оценивает затраты потенциальной энергии-времени. В качестве подынтегральной функции принимается модуль приращения потенциальной энергии ∆ П , величина которой для отдельных звеньев вычисляется по известным формулам.

Удельное действие по Буридану

В качестве подынтегральной функции принимается удельное действие по Буридану К_Б . Используя модуль обобщенной силы Q , возможно оценить затраты импульса сил.

Удельное действие по Кориолису-Понселе

Удельное действие по Кориолису-Понселе рассчитывается на основе модуля произведения обобщенной силы и скорости, т.е. мощности Q , и оценивает затраты механической работы.

Удельное действие по импульсу Ким

Данное удельное действие оценивает затраты импульса сил сопротивления и инерции, приведенные к электродвигателю. Подынтегральной функцией является модуль приведенного к оси электродвигателя момента действующих в системе сил сопротивления и инерции М _ПРИВ .

Под приведенным моментом понимаем момент приведенной пары сил сопротивления и инерции, условно приложенной к валу ротора электродвигателя (звено приведения). Величина этого момента определяется из условия: мощность пары равна сумме мощностей сил и пар сил, приложенных к звеньям механизма [1]:

р  р  р  ррррр  р  р

^1V± прив ^1V± пр + ^{1 y±} кул + ^{1 v±} кф + ^{1 v±} Т + ^{1 v±} ц + ^{1 v±} зв + ^1V1 у + ^{1 v±} пруж + ^{1 v±} тр ’

Выражения моментов сил сопротивления и инерции звеньев, приведенных к ротору, имеет вид: для привода dϕ р d ϕр dt пр пр dt2 n                              1 7

dt для кулачка dϕ

M J" = - { J кул d n - Р л R . кул ""'( ' ■+ Y . )}- dt -;                   (28)

dt                     dϕр dt для коромысла dα м .ор' = -{Jкор da - P~ R   “*& + Y .)i Or;             (29)

dt                      dϕр dt для тяги

„ р ₍ d_Td ² в d e          d a . 1,     „de dq>_P

M_T =- { m_Ta_T + J_TP (cos a + cos p )}/;

Т Т Т Т dt2 dt Т к dt 2 Т И dt dt для цепи

M ' = M / + M / + M ^р =- ( m- l a + H H^-H L ^dH ) + J d- ^ ^{d /!} + ц ^цТ цзв ^цу а ^{цТ цТ ц} dt ²     dt ^цТ dt ² dt

ц(31)

P             dHd

+ J S^ + — x {- 4 /cos edrЛ (К ^in в - R, - Нц)}/;

цзв зв зв   l ц     2 цТ d dt dt цТ           зв ц dt для звездочки dϕ

M звр =- J .-'.">. /      ;

dt для утюга dHц d2 H р               ц         dt

M у     (mу dt2 + P) dn ’ dt для пружины

M ПРУЖ

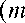
d H пруж

dt2

dt для трения (в направляющих утюга)

M Т _Р ^Р =- K ( M ц^р + M п_Руж^Р ),                       (35)

где d2a da j 2 , 1 da de aT = VstWst =—;--L +---lKlT sin(в - a) x

Т                dt2 dtl к 2 dt dt d β d α                             – скалярное произведение век- da  de      2     24        1 в d2в в x {(   -   ++(-d7T +    )cng(в - a)} +г dt   dt)   d d0    da               4 dt2 dt Т dt dt торов скорости и ускорения центра масс тяги ST (рис. 6);

d 2a da j 2 , в     1

a)T = VS)) WS)) =—Г — + к + —(lT + ~l)T ){—l к sln(e - a) x dt dt dt      2

d² в d a

– скалярное произведение

da   dв.  ddt2    dt2                 d 2 в,,1

x [(“---y) + ( JO + —)ctg(в -a)] + y(lT + l4^)} dt   dt dp    da               dt22 dt dt векторов скорости и ускорения центра масс цепи, присоединенной к тяге;

К – коэффициент, учитывающий трение (значения приведены ниже).

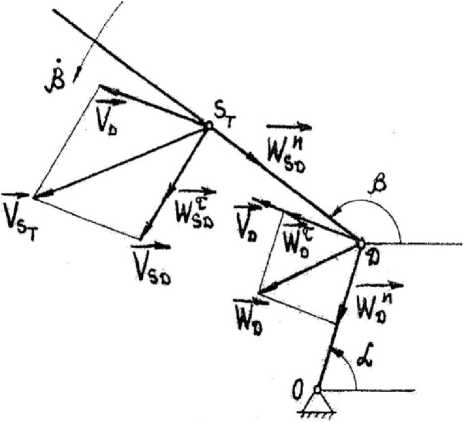
Рис. 6. Схема для определения скалярного произведения векторов скорости и ускорения тяги

Удельное действие по Виттенбауэру

В качестве подынтегральной функции в выражении удельного действия по Виттенбауэру используется произведение модуля приведенного момента (сил сопротивления и инерции) на скорость вращения вала ротора электродвигателя. Данное удельное действие оценивает затраты работы сил сопротивления и инерции.

Удельное действие по Декарту

Данное удельное действие оценивает затраты количества движения-времени звеньев (механизм привода утюга) и его можно представить в виде двух интегралов. В качестве подынтегральной функции первого интеграла берется сумма модулей количества движения звеньев, входящих в механизм. Выражение для определения количества движения будет иметь вид:

для кулачка dH

K у = m у -л

у

;

K к = m -» d^R^ ;                             (36)

для коромысла	d^p K кор    m kop dt R uT-op ’	(37)
для тяги	K T = mTVST ;	(38)

для цепи mu         ^l Ku =    {l^ V^:и +—sin(в - ц          цТ Sцц u da ■ a)---+ Hu dt      ц dH -}г}; dt (39) для утюга для пружины

K

пруж

m пруж

dH

пруж

dt

где V_ST

da |   2   1 | de | 2d da

— I +_l~l It —'тк cos(p - a) — скорость центра масс ST dt J  K 4 < dt J  T   dt K dt TT тяги, м/с;

^{d d}\2 2 dfixlsi   ¹        d ^a(% ^d P ¹

V s™ =i (37) ^l - + ⁽^T ) ^{( l} T + ^l r ) ^-2^T ^l - 7T^{( l} T + ^T ^{)cos( e} — ^{a -} скорость центра V dt         dt 2           dt dt 2

масс S_ЦТ цепи, присоединенной к тяге, м/с.

Подынтегральной функцией второго интеграла является сумма моментов (по модулю) количества движения звеньев. Моменты количества движений будут иметь вид:

для привода	L = J d^- ■ Snn пр dt ’	(42)
для кулачка	L. = J dV- SkKy    ' кул dt ;	(43)
для коромысла	_ da SkK0 = кор ~dt ’	(44)
для тяги	L = j d^- st Tt _,’ dt	(45)
для цепи	d^ L Sц    L sцц + L Sццз   J цТ dt + J цзв ^ зв ’	(46)
для звездочки	L S33 = J зв ^ зв	(47)
	Выводы

В границах математической модели оптимизации динамики механического привода удалось сформировать систему математических моделей и алгоритмы вычисления удельных действий. В результате появилась возможность проводить не только качественный и количественный анализ уровня совершенства механизма, но и осуществлять синтез аналогов имеющих более качественные характеристики.