Формирование многоуровневых структур управления при проведении реструктуризации предприятий связи

Любое предприятие постоянно решает двуединую задачу – движется к достижению своих стратегических целей и адаптируется к изменению окружающей среды. При этом долгосрочные цели развития остаются неизменными, а способы их достижения могут меняться в зависимости от изменения макро- и микросреды. Для предприятий телекоммуникационных систем особое значение имеет влияние научно-технического прогресса, поскольку ни одна отрасль не развивается столь стремительно и, соответственно, эти изменения не могут не отразиться на особенностях формирования структуры управления предприятием, на ее способности адаптироваться к возможным изменениям.

Построение системы управления изменениями заключается в создании многоуровневой структуры управления с использованием процессного подхода. Для предприятий связи, где смена номенклатурных позиций происходит постоянно – это единственно возможный вариант формирования гибкой структуры управления, а следовательно, и эффективного производства.

Анализ способов представления разнохарактерных, слабо формализуемых данных [1-2] показывает, что для решения задачи формирования частных и интегральных показателей функционирования МСУ и ее элементов можно воспользоваться основными положениями теории систем массового обслуживания (СМО) и теории марковских процессов, которые позволяют эффективно описывать стохастические явления и процессы.

Постановка задачи

Процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем; состояние СМО меняется скачком в моменты появления каких-то событий (прихода новой заявки, окончания обслуживания, момента, когда заявка, которой «надоело ждать», покидает очередь).

Математический анализ работы СМО очень упрощается, если процесс этой работы – марковский. Для этого достаточно, чтобы все потоки событий, переводящие систему из состояния в состояние (потоки заявок, «потоки обслуживания»), были простейшими. Случайный процесс, протекающий в системе, называется марковским, если для любого момента времени t ₀ вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент t ₀ и не зависят от того, когда и как система пришла в это состояние.

Пусть в момент t ₀ система находится в определенном состоянии S ₀. Мы наблюдаем процесс со стороны и в момент t ₀ знаем состояние системы S ₀ и всю предысторию процесса, все, что было при t <  t ₀. Нас интересует будущее ( t >  t ₀). В точности невозможно его предугадать, так как процесс – случайный, а значит – непредсказуемый. Но вероятностные характеристики процесса в будущем мы найти можем. Например, вероятность того, что через некоторое время t система S окажется в состоянии S или сохранит состояние S ₀, и т. п.

На практике Марковские процессы в чистом виде обычно не встречаются, но нередко приходится иметь дело с процессами, для которых влиянием «предыстории» можно пренебречь. При изучении таких процессов можно с успехом применять Марковские модели.

Важной характеристикой потока событий является его интенсивность – среднее число событий, приходящееся на единицу времени. Интенсивность потока может быть как постоянной, так и переменной, зависящей от времени t .

Функциональная структура управления

Для простейшего потока с интенсивностью λ интервал между соседними событиями имеет так называемое экспоненциальное распределение с плотностью

f (t) = Xe-^ (t > 0). (1)

Величина λ в (1) – параметр показательного закона. Для случайной величины T , имеющей экспоненциальное распределение, математическое ожидание m_T есть величина, обратная параметру, а среднее квадратическое отклонение σ _T равно математическому ожиданию:

m T =^ t = ^ . . ⁽2)

В теории вероятностей в качестве «меры случайности» неотрицательной случайной величины нередко рассматривают так называемый коэффициент вариации:

Из (2)-(3)следует,что для показательного распределения коэффициент вариации равен 1,то есть для простейшего потока событий коэффициент вариации интервалов между событиями равен единице.

Очевидно,что для регулярного потока событий,у которого интервал между событиями не случайный, коэффициент вариации равен нулю.

Имея в своем распоряжении размеченный граф состояний, можно найти все вероятности состояний pi(t)как функции времени.Для этого составляются и решаются так называемые уравнения Колмогорова – дифференциальные уравнения особого вида,в которых неизвестными функциями являются вероятности состояний.Каждый член равен произведению плотности вероятности перехода соответствующей стрелки,умноженной на вероятность того состояния, из которого исходит стрелка.

Реализация проекта,например,принятия решений по освоению новой продукции в структуре управления предприятием, схематично может быть представлен,как последовательное соединение многоканальных СМО с неограниченной длиной очереди и неограниченным ожиданием каждая (см.рис.1).

Определим основные характеристики изображен-нойсистемыпоследовательныхСМО. Рассмотрим n -канальную СМО,на которую поступает поток заявок с интенсивностью λ (среднее число заявок,поступа-ющих в единицу времени,равно λ); интенсивность обслуживания для одного канала μ ( μ – величина,об-ратная среднему времени обслуживания t _обсл); число мест в очереди неограниченно.Заявка,нашедшая все каналы занятыми,становится в очередь,не которую не наложено ограничений ни по длине очереди,ни по времени ожидания.

Состояния системы нумеруются по числу заявок, связанных системой:

• -    нет очереди:

• -    S ₀ – все каналы свободны;

• -    S ₁ – занят один канал,все остальные свободны;

• -    S _n+1 – все каналы заняты,одна заявка стоит в очереди;

  - S _{n+ m} – все каналы заняты, m заявок стоит в очереди.

вход

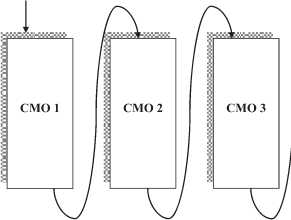
Рис. 1. Общая схема рассмотрения проекта в функциональной структуре управления

Графическое представление такой СМО представлено на рис. 2. По стрелкам слева направо систему переводит всегда один и тот же поток заявок с интенсивностью λ, по стрелкам справа налево систему переводит поток обслуживания, интенсивность которого равна μ, умноженному на число занятых каналов.

Очереди нет

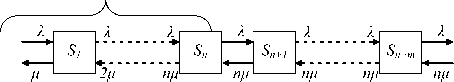
Рис. 2. Схема n -канальной СМО с неограниченной длиной очереди и неограниченным ожиданием

В качестве основных характеристик СМО будем рассматривать: Ротк - вероятность того, что заявке будет отказано в обслуживании; Pобсл – вероятность того, что заявка будет обслужена (или относительная пропускная способность), Робсл = 1_ Ротк ; A — абсолютная пропускная способность, то есть среднее число заявок, обслу- живаемых в единицу времени, A = X • Робсл; z -

Aλ среднее число занятых каналов, z = — = — • робсл;

μμ q - доля каналов, занятых обслуживанием, q = — ; r - среднее число заявок в очереди; k -n среднее число заявок в системе, k = r + z; tож - среднее время ожидания заявки в очереди,

r t ож —

X

; t обсл - среднее время обслуживания заявки, tобсл =

P

—обсл ; t смо - среднее время пре-

Ц _       _     _ бывания заявки в СМО, 1смо = 1ож +1обсл.

Математическая модель

Из рис. 3 видно, что процесс, протекающий в СМО, представляет собой частный случай процесса гибели и размножения. Для получения его характеристик рассмотрим сначала n -канальную СМО с ограниченной длиной очереди (см. рис. 3).

Уравнения Колмогорова для вероятностей состояний рассматриваемой СМО примут вид:

dpdtt ) = H P i ⁽ t ) -X Р о ⁽ t ) ,

ddp=x Pk-i (t)+(k+1) ^ Pk+i (t) - ( x+k н) Pk (t), dpn (t)                        / x                          (4)

—dp = X Pn-1 ( t ) - nH Pn ( t ) ,

—^ = X Pn ( t ) - nH Pn+1 ( t ),

dPn+^ = X Pn+m-1 ( t ) - nH Pn+m ( t ).

Уравнения (4) являются уравнениями Эрланга. Естественными начальными условиями для их решения являются:

Po ( 0) = 1, Р1 ( 0) = P2 ( 0 ) = - = Pn ( 0 ) =

= P n + 1 ( 0 ) = ••• = P n + m ( 0 ) = 0 ,

которые соответствуют тому, что в начальный момент система свободна.

Расчет основных характеристик

Определим характеристики эффективности системы.

Вероятность отказа: поступившая заявка получает отказ, если заняты все n каналов и все m мест в очереди:

р П + т

^Р отк = P n + m =       P 0 "

n ^m n!

Относительная пропускная способность дополняет вероятность отказа до единицы:

Рис. 3. Схема n -канальная СМО с ограниченной длиной очереди

обсл

р П + т

1 - ротк =1 —m  Po n n!

Абсолютная пропускная способность СМО:

Интегрирование (4) в аналитическом виде довольно сложно, поэтому на практике такие системы дифференциальных уравнений обычно решаются численно. Наибольший интерес для практики имеют предельные вероятности состояний, характеризующие установившийся режим работы СМО. Для нахождения предельных вероятностей воспользуемся уже готовым решением задачи, полученным для схемы гибели и размножения [3-7]:

A=λP обсл

=λ

1 -

n+m

ρ

m nn

p ₀

Среднее число занятых каналов:

n + m                  n + m

A λ⎛ρ ⎞⎛ρ ⎞ z = _ = _ 1--Pn = P 1--Pn ■ m0m0

ц ц^    n n ! J ^ n n ! J

Среднее число заявок в очереди можно вычислить непосредственно как математическое ожидание дискретной случайной величины:

P k =^pr P o , ^k = 1, n;

k! n+i ⎪ρ

P n+i =— P o , i = 1, m; n ⁱ n!

=________________________1_______________________

⎪_⎪ p 0       ρρ 2 ρ n ρ n + 1 ρ n + 2 ρ n + m

5   1 + — + — ++ — + -— + -4— ++ -—

1! 2! n! nn! n ² n! n^m n

=__________________________1 .

m +1

⎪                                          ρ_- ⎛_⎜ρ⎞_⎟

^⎪    ρρ ²     ρ ⁿ ρ ⁿ nn

1 + — + — + _ + — + -—

1! 2! n! n!1

⎪⎩

_                                         m       n+i r = 1Pn+1 + 2Pn+2 + .„ + mpn+m = ^i • -    Po = i=i n • n!

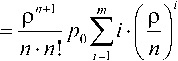
- i

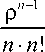
m

Po Z i -x- i=1

m где x = / ■ Для определения суммы Z i" Xi"1 i=i

воспользуемся производной суммы геометрической прогрессии:

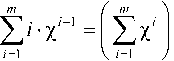
' x ( 1 -x m ) ' , ( 1 ^-x ) ,

1 -x m ( m + 1 -mx )

В этих формулах интенсивность потока заявок λ и интенсивность потока обслуживаний (для одного канала) μ не фигурируют по отдельности, а входят только своим отношением ^λ _μ . Обозна- λ^μ чим это отношение: ^ρ= _μ и будем называть величину ρ «приведенной интенсивностью» потока заявок. Физический смысл ее таков: величина

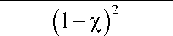
Таким образом r =

p^ l p o 1 -X m ( m +1 - m X ) nn !          ( 1 -x ) 2

ρ представляет собой среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки.

Среднее число заявок в системе: k = r + z .

Определим среднее время ожидания заявки в очереди. Рассмотрим ряд ситуаций, различающихся тем, в каком состоянии застанет систему вновь пришедшая заявка и сколько времени ей придется ждать обслуживания.

Если заявка застанет не все каналы занятыми, ей не придется ждать (соответствующие члены в математическом ожидании равны нулю). Если

заявка придет в момент, когда заняты все n каналов, а очереди нет, ей придется ждать в среднем время, равное (потому что «поток освобождений» n каналов имеет интенсивность nμ ). Если заявка

застанет все каналы занятыми и одну заявку перед собой в очереди, ей придется в среднем ждать в течение времени ² _nμ (по ¹ _nμ на каждую впереди стоящую заявку) и т. ^μ д. Если заявка застанет в очереди k заявок, ей придется ждать в среднем в течение времени ^k _nμ . Если вновь пришедшая заявка застанет в очереди уже m заявок, то она вообще не будет ждать (но и не будет обслужена). Среднее время ожидания найдем, умножая каждое из этих значений на соответствующие вероятности:

В СМО с неограниченной длиной очереди и неограниченным временем ожидания каждая заявка рано или поздно будет обслужена, поэтому ^Р обсл = ¹ , а ^Р отк = ⁰ , A = ^X' ^Р обсл =^X , в среднем непрерывно занятый канал будет выдавать ^λ_μ =ρ обслуженных заявок в единицу времени.

Среднее число заявок в очереди можно вычислить непосредственно как математическое ожидание дискретной случайной величины:

w               to

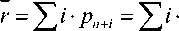
i =1                   i=1

_ n+1 ρ to

⋅p 0 ⋅ ∑ i⋅

^!              i=1

p n+i

n⋅n

⋅p0 =

ρ

i-1

t ож

12   m

=--Pn +--Pn+1 + - +--Pn+m-1 =

nμnμ         nμ

1 Ip"        . p""

--1 — Po + 2--Г Po + - + m пц^ n! nn!

n

m - 1

n

_ n+m-1 ρ p0

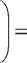
n⋅n

_ n+1

P

n⋅n

n

to

• Po • Xi"Xi-1

i=1

n ρ p ₀

n ц n!

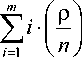
n ρ p ₀

n ц n!

m

X i -xi-1 =

to

Выражение X i "X-1 представляет собой про- i =1

изводную суммы бесконечной геометрической прогрессии. Учитывая требование х = рП < 1, сумма бесконечно убывающей геометрической iχ прогрессии равна ∑ χ= , а ее производная i=i       1 - X

pnPo 1 — Xm (m +1 - mX) n ц n!      (1 -x )2

_ рП+1            1

имеет вид. Таким образом, r =ρ ⋅ p ₀ ⋅       ₂

n •n!       (1 -X)

Используя аналогичные рассуждения, получим

Среднее в р емя пребывания заявки в системе: t СМО = t ож + t обсл -

Для расчета характеристик СМО с неограниченной длиной очереди и неограниченным ожиданием будем использовать полученные ранее соотношения при m → ∞ .

Вероятности состояний получим изформул (5) предельным переходом (при m → ∞ ). При этом заметим, что сумма соответствующей геометрической прогрессии сходится при х < 1 и расходится при х < 1. Поэтому требование X = ^Р< 1 ⁿ является обязательным для получения конечных значений вероятностей состояний. Таким образом, выражения для предельных вероятностей состояний примут вид:

среднее

Среднее

Среднее

время ожидания: tож число занятых каналов:

Pn Po 1

=

npn! (1 -x)

- A X z=-=-=p. p p

число заявок, связанных с СМО:

ρk

Рк = 77 Po, k = 1, n;

k!

n+i

ρ

Pn+i = - Po, i = 1,2, n n!

;

k = r + z .

На основании приведенных выше формул для расчета основных характеристик СМО с неограниченной очередью и неограниченным временем ожидания могут быть рассчитаны все характеристики процесса, представленного на рис. 3. Каждая частная СМО обладает своими параметрами и характеристиками. Однако, учитывая,что в среднем непрерывно занятый в каждой СМО канал будет выдавать ^λ _μ ^=ρ обслуженных заявок в единицу времени, вся СМО будет выдавать ρ⋅ n заявок в единицу времени, которые и будут поступать в следующую СМО. Таким образом, интенсивность поступления заявок в каждую последующую СМО будет зависеть от двух величин: интенсивности поступления заявок в первую СМО и от количества

p 0      2 nn + 1

ρρ ρ ρ

1 + +   + . . +   + у----7

1! 2!        n! n!( n-p)

выдаваемых заявок в единицу времени предыдущей СМО, а именно, интенсивность поступления заявок в каждую последующую СМО определяется как минимум из указанных двух величин. Дей- ствительно,если предыдущая СМО обрабатывает заявки быстрее, чем они поступают, то среднее количество заявок в единицу времени,поступающее в последующую СМО, не может быть больше, чем количество заявок, поступающих в единицу времени в систему. Пример расчета характеристик процесса представлен в таблице 1.

Таблица 1. Пример расчета характеристик процесса

Параметры СМО	СМО 1	СМО 2	СМО 3	СМО 4	СМО 5	СМО 6	СМО 7
n	4	4	5	4	5	5	5
λ	0,1	0,1	0,1	0,1	0,1	0,1	0,1
μ	0,09	0,11	0,11	0,13	0,25	0,20	0,20
ρ	1,10	0,90	0,90	0,80	0,40	0,50	0,50
χ	0,28	0,23	0,18	0,20	0,08	0,10	0,10
р отк	0	0	0	0	0	0	0
Р- обсл	1	1	1	1	1	1	1
A	0,1	0,1	0,1	0,1	0,1	0,1	0,1
z	1,1	0,9	0,9	0,8	0,4	0,5	0,5
q	0,275	0,225	0,18	0,2	0,08	0,1	0,1
r	0,0106	0,0042	0,0005	0,0024	0,0000	0,0000	0,0000
k	1,1106	0,9042	0,9005	0,8024	0,4000	0,5000	0,5000
t ож	0,1060	0,0416	0,0054	0,0240	0,0001	0,0002	0,0002
t обсл	11	9	9	8	4	5	5
t СМО	11,106	9,042	9,005	8,024	4,000	5,000	5,000

Просуммировав все элементы строк « t ож »,

« t обсл » и « t СМО », можно рассчитать время ожидания, обслуживания и пребывания заявки во всех СМО. Для рассмотренного примера перечисленные величины составили 0,177; 51,0 и 51,177 единиц времени, соответственно. Помимо этого, рассчитанные характеристики всех СМО дают информацию, являющуюся основой для принятия управленческих решений.

Выводы

Таким образом,можно утверждать,что применение методов теории Марковских процессов и систем массового обслуживания позволяет эффективно решать задачи совершенствования организационной структуры управления предприятием с учетом риска.