Формирование начального распределения компонентов плазмы на фазовой плоскости в методе крупных частиц при электродуговом синтезе УНС

Исследование процесса синтеза углеродных наноструктур (УНС), обладающих уникальными свойствами, является актуальным направлений развития современной науки. Практическое применение их в качестве небольших добавок (0,01 % - 5 %) в полимерные смолы уже позволяет получать различные полимерные нанокомпозиты с комплексом новых (электропроводность, огнестойкость) или улучшенных свойств (увеличение запаса прочности, жесткости, повышение формоустойчи-вости, барьерных качеств) [1].

Рост современного промышленного производства УНС сдерживает низкая эффективность существующих технологий синтеза из-за недостаточной изученности механизмов образования кластерных групп формирующих УНС (фуллерены, нанотрубки, нановолокна) на основе взаимодействия атомов углерода [2].

Одной из перспективных технологий синтеза УНС высокого качества является метод термического распыления графита в низкотемпературной плазме в среде буферного газа [3]. Использование плазмы электродуго-вого разряда характеризуется большим количеством различных эффектов взаимодействия частиц происходящих при фазовых и структурных превращениях углерода в многокомпонентной плазме и на поверхности катода. Все это, а также высокий порядок частиц в многокомпонентной плазме (~10E16-10E17), требующие значительные затраты машинного времени для численного расчета, определяет трудности моделирования данного процесса.

Одним из способов моделирования коллективных явлений в плазме является метод кинетического описания, использующего изменения функций распределения частиц до и после столкновений.

В основу разрабатываемой математической модели кинетики движения и взаимодействия частиц многокомпонентной плазмы в инертном газе, с учетом парных упругих и неупругих столкновений, положена система кинетических уравнений Больцмана для каждой компоненты плазмы с учетом интеграла столкновений, дополненная системой уравнений Максвелла [4, 5].

Решение системы уравнений Больцмана-Максвелла предполагает использование численных методов. За основу решения поставленных задач был взят метод «крупных частиц» (МКЧ), позволяющий значительно сократить объем вычислений и снизить требования к вычислительным ресурсам [6]. Главная идея МКЧ состоит в том, что фазовое пространство плазмы в начальный момент време ни разбивается на отдельные ячейки, в которых вместо реального числа частиц определенного вида в соответствии с начальной функцией распределения каждой компоненты f(г, «9,0) рассматривается макрочастица, т.е. укрупʜeʜʜaя чaстицa с суммaрным зaрядом и массой всех частиц данного сорта, содержащихся в одной ячейке. После расчета траектории движения крупной чaстицы под действием электромагнитного поля, её нового положения в фазовом пространстве в последующий момент времени, на основе текущей функции рaспределения производится рaзнос зaрядa частицы по узлам фазового пространства, и процесс повторяется. Для этого используется CIC алгоритм МКЧ для трехмерного пространства (рисунок 1) [7].

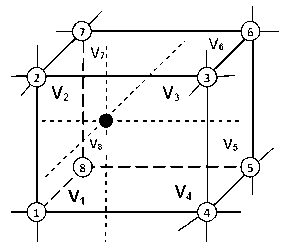
Рисунок 1. CIC алгоритм МКЧ

В трехмерном случae зaряд рaзносится по узлaм пропорциoʜaльно объему V i :

V = у Vi, i=1

qd = qV; d = i-8         (1)

qi = qa 'a, где qd - разнесенный заряд макрочастицы в узле; qi - заряд макрочастицы в ячейке.

Концентрaция чaстиц сортa α в кaждой ячейке:

П а = f f a ( 9 )d 9 , V

где а = e, c, h (e - электрон, h - ион гелия, c - ион углерода).

Условия сходимости и адекватности решения используемого МКЧ [8] следующие:

- шаг интегрирования должен быть мно го меньше минимального характерного времени процессов в плазме (колебаний плазмы -Ленгмюровские волны):

A t <  3.4 — , ^ = 5.64 - 10⁴Т й"        (₃)

to p                                , где гор - плазменная частота, ne - концен трация электрона.

- шаг сетки должен быть меньше радиуса Дебая:

h < 0.2XD ,                (4)

где X D - радиус Дебая.

Использование МКЧ позволяет сократить количество однотипных вычислений.

На рисунке 2 приведена общая расчетная схема метода крупных частиц.

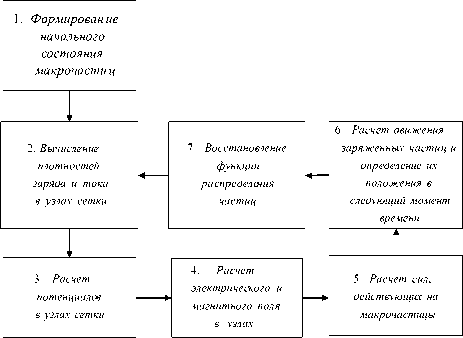
Рисунок 2. Расчетная схема метода крупных частиц

Частицы, моделирующие плазму, располагаются внутри ячеек. Каждая частица имеет свою скорость, которая при движении изменяется под действием электрического поля и за счет взаимодействия с другими частицами.

На первом этапе производится распределение частиц в ячейках, моделирующих плазму. Координаты х “ (0), y j (0), z “ (0) и скорости v “ (0) частиц задаются с использованием датчиков случайных чисел. Нижний индекс j указывает номер частицы, а а = e, c, h . Значения v “ (0) формируют распределение, задаваемое максвелловской функцией f ( r , 5 ,0) . На рисунке 4 представлено начальное распределение частиц в фазовом пространстве. В начальный момент времени считается, что электроны и атомы инертного газа - гелия занимают все межэлектродное пространство, а ионы углерода распределены на границе поверхности торца анода (ось ординат).

Важное место в использовании МКЧ для расчета синтеза наноструктур электродуговым методом занимает задача о начальном распределении компонентов плазмы.

Используемая расчетная сетка фазового пространства представлена на рисунке 3.

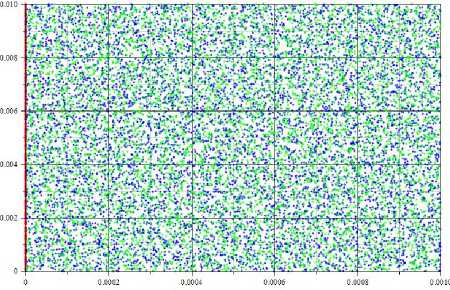
Рисунок 4. Начальное распределение компонентов плазмы

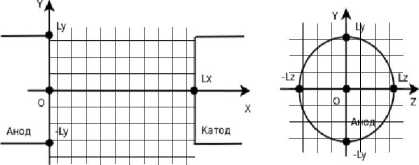
Рисунок 3. Расчетная сетка

Область решения имеет форму параллелепипеда. В ней вводится декартовая система координат (x,y,z). Вся область разбита на ячейки с размерами hx, hy, hz вдоль соответствующих направлений:

На следующем этапе в соответствии с начальной функцией распределения каждой компоненты плазмы считается число частиц сорта а в каждой ячейке. Для этого сначала необходимо определить ближайшие к частице узлы сетки или ячейку сетки, в которой находится частица. В случае прямоугольных ячеек расположение частицы находится в три операции (6-8):

i =

⁽ x ^- x ₀)

+1 ,

hx =

Lx n +1,

к =

⁽ У ^- У 0 ) h y

+ 1,

h y

hz =

L y

m +1

L z

b +1

l =

^{( z - z} 0 )

hz

+ 1,

где L x , L y , L _z - размер расчетной области; n, m, b - количество задаваемых узлов.

где i,k,l - номер ячейки прямоугольной сетки, (x,y,z) координаты частиц, (x₀,y₀,z₀) - координаты начала сетки, h x ,h y , h_z - шаг ячейки. Здесь операция в квадратных скобках [...] означает взятие целой части.

На следующем этапе суммируются заряды

всех частиц данного сорта, содержащиеся в одной ячейке, суммарный заряд присваивается одной модельной (крупной) частице данного сорта.

Для определения координат центров крупных частиц в ячейках используются формулы нахождения центра масс. В системе ма-

Количество эмиссионных ионов в единицу времени в ячейке при равномерном за

коне выгорания анода:

nc =

^ПСА ' ^Ly ' ^Lz n R A

териальных точек координаты центра масс определяются по формулам (9-11):

x _c

yc

zc

Е mi ■ x

Е mi

i

Е mi ■ y.

i ___________________

Е m. ’

i

Em,■ Zj l I i___________________

Е m- ’

i

где Е ^mi - суммарная масса системы; x . , y . и i

z . - координаты i -й материальной точки; m . - мас

са i -й материальной точки.

Исходя из суммарного объема, занимае

мого частицами, определяются условные радиусы крупных частиц (12):

3 ■ х -

R K4 =

4 з

- ■ п ■ R_a ³ ■ N

. 3                         .

4 ■ п

1 3

V                      7

где R _a - радиус частиц; х - коэффициент учи-

тывающий задаваемую плотность частиц в макрочастице ( х ~ 6...10);-N - число частиц в крупной частице).

Количество эмиссионных электронов в единицу времени в межэлектродное простран

ство с торца катода:

neK

Т А

, e

где I - сила тока дуги, At=h_t - шаг интегриро

вания по времени, e - заряд электрона.

Количество эмиссионных электронов в единицу времени в ячейке:

ne

где R_K - радиус катода.

n eK • L y • ^Lz ^{n R}K

Количество эмиссионых ионов углерода

в единицу времени при разрушении анода:

n СА

9 a А А , me ’

где 9 A - скорость выгорания анода по экспе

риментальным данным, m_C - масса атома углерода, At- шаг по времени интегрирования.

где R _a - радиус анода.

Общее число атомов буферного газа K g в межэлектродном пространстве:

PVM

^K G =                       (17)

RTmg где P - давление газа в камере, V - объем межэлектродного пространства, R - газовая постоянная, T - температура, M - молярная масса буферного газа, mg - масса одного атома буферного газа (гелия).

Общее число ионов буферного газа определяется из условия квазинейтральности плазмы:

N g = N e — N c              (18)

, где Ne, NC - общее количество электронов и атомов углерода в плазме.

На рисунке 5 представлено полученное начальное распределение крупных частиц атомов гелия и ионов углерода для давления в камере синтеза буферного газа при Р=100 Торр и диаметре углеродного электрода d=10E-3м.

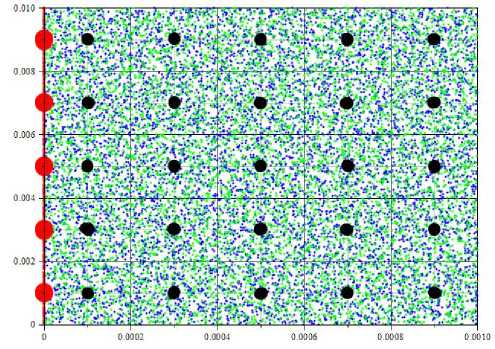
Рисунок 5. Распределение крупных частиц атомов углерода и гелия для t=0

Формирование начального распределения компонентов плазмы на фазовой плоскости определяет движение и условия взаимодействия частиц многокомпонентной плазмы в инертном газе, что позволяет определять зоны, удовлетворяющие энергетическим условиям вероятного формирования в плазме кластерных групп углерода со связями С-С, С=С или С=С-С, участвующих в синтез УНС.