Формирование нестационарных режимов при моделировании аспирационных течений: неустойчивость Кельвина - Гельмгольца

Проблема очистки воздуха при производстве металла представляется насущной, и для ее решения рассматриваются различные подходы [4; 9; 11]. Для определения эффективности аспирационной системы, перед изучением динамики примесей, необходимо построить поле скоростей воздуха [3; 10]. В то же время методы анализа аспирационных течений, основанные на газодинамическом подходе, только начинают развиваться [1; 7]. Традиционными являются подходы, основанные на аппарате потенциальных течений [7; 13].

Одним из возможных решений является использование специальных вытяжных устройств, установленных в непосредственной близости от печи (см. рис. 1, устройство A ). Для повышения эффективности очистки можно установить дополнительный вентилятор (устройство B на рисунке 1). Такая конфигурация способна существенно отклонять горячий и загрязненный воздух, поднимающийся от печки, увеличивая долю газа, который засасывается устройством B .

Особая сложность моделирования такого рода течений связана с наличием многосвязных двумерных и трехмерных областей с разрезами внутри расчетной зоны. В данной работе, используя прямые методы численного газодинамического нелинейного моделирования, изучены некоторые особенности поля скоростей в воздухе внутри металлургического цеха, где установлена аспирационная система, изображенная на рисунке 1.

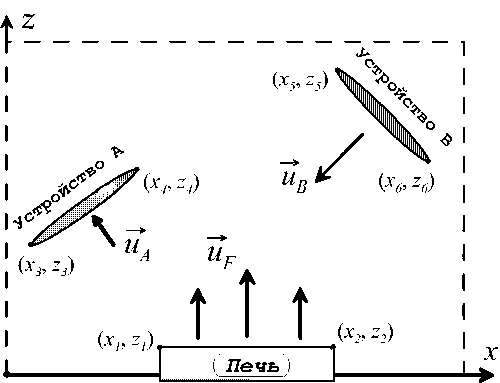
Рис. 1. Схема аспирационной системы:

горячий воздух поднимается от «Печи». «Устройство A » ( вентиляционный зонт ) вытягивает газ. «Устройство B » ( аэратор ) создает дополнительный поток воздуха, повышая эффективность очистки воздуха

Газодинамическая модель воздушных потоков

Будем исходить из нестационарной гидродинамической двумерной модели, описываемой системой уравнений:

^{д р} + d^{iv (} р - а ) = Q ⁽ х , z ), д t

ди   ^_

— + (u-^У и ^- Qu, д t

—+u -Vp+y - p v а=qe , dt где        p - плотность воздуха;

• p – давление;

U = { и_х , u z } — вектор скорости;

• Y = 1,42 - показатель адиабаты;

• V - дифференциальный оператор набла;

• Q , Q_u , Q_E – функции источников.

В основе численной модели лежит алгоритм TVD в декартовой системе координат [5], который продемонстрировал свою эффективность для широкого круга задач [2]. Внутри расчетной области задаем положения аспирационных устройств A, B и печи набором координат {xj, zj}, которые определяют отрезки LF, LA, LB, вектора иF(х, z), иA(х, z), иB(х, z) вдоль линий LFAB(х, z) (см. рис. 1). В качестве начального состояния выбираем момент одновременного включения потока воздуха от печи ЦF(х, z) и устройств A и B.

Результаты численного моделирования

На рисунке 2 показана типичная структура аспирационного течения по результатам численных расчетов. К числу свободных параметров относятся: { X j , z j }, профили скорости U i F ( х , z ), U A ( х , z ), й B ( х , z ). В зависимости от параметров системы возможны два режима течения, когда воздух из устройства B затягивается устройством A , и когда этого не происходит.

В расчетной области имеется два четко выделенных потока: 1) устройство A непосредственно перехватывает воздух от печи, что формирует первую струю; 2) второй поток генерируется устройством B . Последний взаимодействует с первым, сильно отклоняя его вправо (см. рис. 1 и 2).

Имеется переходная зона между этими двумя потоками, в которой тангенциальная компонента скорости воздуха сильно меняет свое значение. Типичная ширина зоны составляет 0,5–1,0 м. Именно из-за неустойчивости Кельвина – Гельмгольца, несмотря на стационарный режим работы Печи и Устройств А , В , расчеты демонстрируют отсутствие стационарной картины. В более реалистичной модели Печи, где поток не задается, а моделируется свободная конвекция, нестационарные процессы должны усиливаться. Этому будет способствовать переход от 2D-моделей к 3D.

Если устройство В не работает, то примерно только половина потока от печи засасывается в устройство А (рис. 2, а ). При включении В ситуация качественно меняется, работа устройства способна обеспечить почти полный перехват воздуха от печи (рис. 2, в , г ). Рисунок 2, б демонстрирует наличие вихревых структур в аспирационном течении.

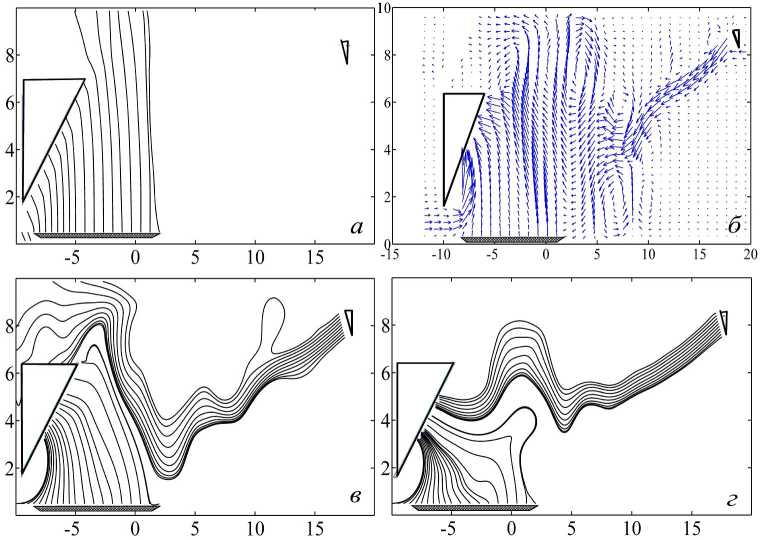
Рис. 2. Структура течения воздуха в различные моменты времени для аспирационной системы, изображенной на рисунке 1. Показаны линии тока ( а , в , г ) и поле скоростей ( б ).

Расстояния указаны в метрах

В зоне переход~а от потока А к потоку B запишем уравнения для малых возмущений давления ~p и смещения ξ вдоль направления r dp =(® - kV(r))2 p0<~ dr

dξ~

= dr p0 (го - kV (r))

где r – координата, перпендикулярная переходной зоне («тангенциальному разрыву», ТР);

• to - собственная частота;

• V ( r ) – профиль скорости в зоне ТР;

k – волновое число вдоль поверхности разрыва. Область тангенциального разрыва скорости является неустойчивой с инкрементом, который пропорционален скачку скорости Im( ro ) = I V 1 - V 2 к [6]. Наличие в реальной системе конечной переходной зоны шириной / уменьшает инкремент неустойчивости, но для типичных значений параметров рассматриваемой задачи при к £ <  1 условия для неустойчивости сохраняются, поскольку по порядку величины имеем Im( ro ) ~ к А V (1- к I ) . Возникновение гидродинамической неустойчивости и последующая турбулизация вещества способны существенно усложнять динамику примесей [8; 12].

Заключение

Сформулируем основные выводы:

• 1.    Для расчета аспирационных течений предложен метод прямого гидродинамического моделирования на основе численного интегрирования полной системы уравнений газодинамики, показавший свою эффективность при проектировании аспирационных систем для задач очистки воздуха в промышленных помещениях.

• 2.    Проведенные расчеты показывают, что использование дополнительных аэраторов может увеличить эффективность очистки воздуха от металлургической печи.

• 3.    Месторасположение аспирационных устройств, их геометрия и мощность существенно влияют на долю очищаемого воздуха, что ставит задачу оптимизации параметров системы. Построенная модель ляжет в основу изучения динамики газовых примесей и аэрозолей для задач оптимизации при проектировании аспирационной системы.

• 4.    Характерной особенностью моделируемого течения оказывается нестационарный характер поля скоростей воздуха даже без учета нестационарного конвективного потока горячего воздуха от печи. По-видимому, причина отмеченной нестационарности течения связана с нелинейной стадией развития неустойчивости Кельвина – Гельмгольца.

ПРИМЕЧАНИЕ

• ¹    Работа частично поддержана грантом РФФИ № 11-07-97025, ФЦП «Научные и научно-педагогические кадры инновационной России» (гос. контракт № 02.740.11.5198).