Формирование оптических сигналов, переносящих ОУМ, на основе вихревых оптоволоконных периодических структур

Электромагнитные волны переносят как энергию, так и импульс, причем импульс включает в себя линейный импульс P и угловой момент L . В частности, угловой момент имеет составляющую, связанную с поляризацией, спиновым угловым моментом (SAM), и другую составляющую, связанную с пространственным распределением поля, которая называется «орбитальный угловой момент» (ОУМ). В оптическом вихревом излучении плоскости постоянной фазы электрического и магнитного полей образуют вихревую структуру, движущуюся в направлении распространения сигнала. ОУМ характеризуется числом, называемым топологическим зарядом, указывающими количество поворотов, которые поле совершает на одной длине волны. Потенциал применения OУM в области коммуникаций огромен, даже несмотря на то, что до полного развертывания ОУМ-сетей еще предстоит решить ряд проблем.

Одной из основных проблем при разработке систем связи на основе OУM сигналов является генерация волн со спиральным волновым фронтом. Существует два основных подхода: решения на основе оптики в свободном пространстве (free space) и методы волоконной оптики. В рамках первой группы можно выделить следующие подходы:

Математическая модель ВВБР и ее параметры

Как было показано во введении, формирование вихревого оптического излучения в оптоволокне является на данный момент малоизученной и актуальной научно-технической проблемой. В данной статье предлагается способ генерации ОУМ-мо-ды первого порядка, основанный на использовании вихревой волоконной брэгговской решетки (ВВБР), которая в общем случае представляет собой непрерывную дифракционную волоконную структуру, имеющую спиральную форму. Классические волоконные брэгговские решетки, представляющие собой дискретный набор штрихов [7], могут быть описаны, например, с помощью подхода, аналогичного описанию туннельного эффекта в квантовой механике [8], однако более общепринятым подходом в описании ВБР является теория смешанных мод. Генерация ОУМ-моды в данном контексте фактически означает конвертирование фундаментальной моды в моду высшего порядка: необходимо добиться преобразования моды ОУМ0 в ОУМ1, поэтому математическая модель ВВБР основана на вышеупомянутой теории смешения мод. Известно, что для существования вихревого излучения необходим маломодовый режим, т. к. любая ОУМ-мода ненулевого порядка представляет собой суперпозицию ТЕ и ТМ мод [9]. Таким образом, для работы в оптическом С-диапазоне (1530–1565 нм) нужно использовать специальные волокна, являющиеся маломодовыми на данном участке спектра, например ступенчатое FMF компании OFS. Для данного волокна применимо приближение слабонаправляющего волокна, т. е. волокна, у которого разность показателей преломления сердцевины и оболочки меньше 1 %. В таком случае для описания модового состава (в том числе и ОУМ-мод) можно использовать аппарат бесселевых функций и линейно-поляризованных (LP) мод [9]. Итак, используя приближение слабонаправляющего волокна, постановку задачи можно сформулировать следующим образом: необходимо разработать решетку, преобразующую ОУМ-моду нулевого порядка (LP01):

E 01 ( r , Ф , z ) = e ‘

J 01⁽ u 01 )

i " ⁰¹ z _т       a. , ⁰ <  r <  r co ,

J 01⁽ u 01 )

в ОУМ-моду первого порядка (ЬЕЦ + i ЬЕ ^ ):

J 11^{( и} ы ч .

E₁ ^r , ф , z) = e i ^P» z          a e i ^ф , 0 <  r <  r „,

¹¹                   J ц( u 11 )                  co

ВВБР

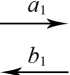
Рис. 1. ВВБР как четырехполюсник

Fig. 1. Chiral fiber Bragg grating as a quadripole

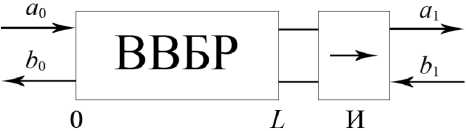
Рис. 2. ВВБР и изолятор для борьбы с переотражениями ВВБР имеет вид, представленный на рис. 3

Fig. 2. Chiral fiber Bragg grating and an insulator for combating multiple reflections of chiral fiber Bragg grating has the form shown in Fig. 3

где r _co – радиус сердцевины (поскольку решетка существует только в сердцевине волокна).

Вихревую волоконную брэгговскую решетку можно рассматривать как четырехполюсник протяженностью от 0 до L (рис. 1), описываемый передаточной матрицей Т , где а 0 - падающее излучение (ОАМ = 0); b 0 - отраженное излучение (ОАМ = 1); а 1 - прошедшее через решетку излучение; b ₁ – это излучение, падающее на решетку со стороны приемника; в общем случае излучение b ₁ возникает вследствие рэлеевского рассеяния или при дуплексной связи.

Данное излучение приведет к формированию отраженного сигнала в направлении b ₁, что в целом является нежелательным обстоятельством, т. к.

в решетке возникнет дополнительное маломощное излучение, т. е. шум. Избавиться от b 1 можно, разместив за решеткой оптический изолятор (рис. 2).

Таким образом, выражая излучение в конце решетки ( z = L ) через излучение в начале решетки ( z = 0), можем записать:

a 1        a 0

[ b. Г T [ b 0 J

представив матрицу Т в виде

T =

( T 11 T 12

T₉₁ T₉₉ ^ 21   22 J

w z Л

w *

Для нахождения этих коэффициентов используем подход, изложенный в [10; 11], а именно – теорию связанных мод [12; 13], а также модель смешения полей при возмущениях показателя преломления, рассмотренную в [14]. Согласно этим подходам, коэффициент отражения поля фактически есть комплексное число, определяемое через матрицу F, рассмотренную в [13] и связывающую излучение

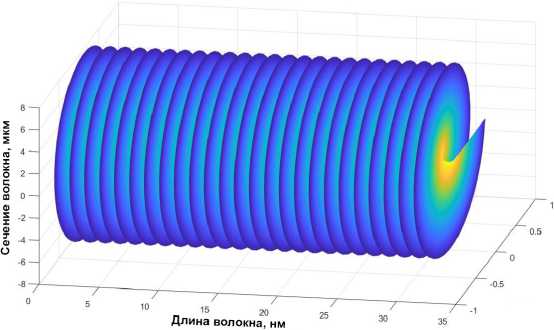
а

Рис. 3. Внешний вид регулярной ВВБР ( а ) и чирпированной ВВБР ( б )

Fig. 3. External view of a regular chiral fiber Bragg grating ( a ) and a chirped chiral fiber Bragg grating ( b )

б

в начале решетки Е (0) с излучением в конце решетки E ( L ): Е (0) = F-E ( L ). В отличие от подхода, предложенного в [13], найдем матрицу Т , связывающую

X X         „ itos                          *

kab = 2 J J5 n2 (r, ф) Ea (r, ф)- Eb (r, ^d Ф,(5)

—X —X

отраженное и прошедшее излучение через пада-

или в случае LP-мод:

ющее излучение. Фактически матрица Т является обратной матрице F : T = F -1 . Согласно правилу на-

хождения обратных матриц, получим:

T =

Г т

T 11

T ₂₁

F 22

—

F ₁₂

У

( T 12

Т99

²² у

к

F ₂₁

F ₁₁

У

Итак, с учетом (1) и (2) можем записать: a 1 = T 11 a 0 + T 12 b 0 = F 22 a 0 ^— F 12 b 0 , ^b 1 = T 21 a 0 + T 22 ^b 0 = ^— F 21 a 0 + F 11 ^b 0 •

X X         „ itoS— kab = _2"° J J 5n(r, ф)E11 (r, ф) • E01 (r, Ф)drdф.(6)

—X —X

Легко показать, что | w |² + z |² = 1, т. е. сумма квадратов модулей коэффициентов отражения и передачи равна единице. Отметим, что в случае отсутствия смешения полей ВВБР действует как регулярная ВБР, не изменяя структуры отражен-

Принимая во внимание, что b 1 = 0, с учетом (3) можно показать, что уравнения для смешанных мод в случае ВВБР остаются такими же, как и для регулярной ВБР, поэтому с учетом [13] получим:

ного поля.

Показатель преломления вихревой брэгговской решетки запишем в виде

n ( r , ф , z ) = n 0 + A n e i ^ ⁰ z g ( z ) f ( r ) e^lm ^ф + к.с

F22__q       ^— k ab ^{sinh( Y L} )

b ⁰ = ^{wa 0} = ^{a 0} f ₁₁ = ^{a 0} у _C0Sh₍ y l ) + i _Ap _sinh( у l ),

— i Pp L

1                       y e ⁰

a = z a = a = a_n------------------------ ,

F_n         y cosh( y L ) + i AP sinh( у L )

где Д р , согласно [11], для встречно распространяющихся мод равно:

AP = P 01 + Р_И — 2 Р 0 •

В формуле (4) w – коэффициент отражения; z * - коэффициент передачи; параметр Р 0 определен ниже и включает в себя Л - период решетки: Л = Х в / 2 n 0 , Х в - брэгговская длина волны отражения; Р 01 и Ри - коэффициенты фазы падающей (ОАМ = 0) и отраженной моды (ОАМ = 1) соответственно. Параметр у определен как у ² = к ^ь — Ар ² • В выражении (4) k ab - комплексный интеграл наложения (определяющий коэффициент смешения), определяемый неоднородностью показателя преломления [14]:

где A n - амплитуда модуляции показателя преломления; P 0 = 2п / y ( z ), y ( z ) - функция чирпирования (рис. 3, б ), имеющая в общем случае произвольный вид, например y ( z ) = Л + Л 0 z (в отсутствие чирпирования y ( z ) = Л ); g ( z ) - функция аподизации, которая в данном случае равна 1 (аподизация отсутствует); f ( r ) - радиальная функция, определяющая, согласно (5), степень смешения мод.

С точки зрения теории смешанных мод, используемой для описания брэгговских решеток, смешение мод происходит при отличном от нуля поперечном возмущении показателя преломления (согласно (5)). Поскольку в классической (невихревой) брэгговской решетке функциональное поперечное возмущение (как функция радиуса волокна или угла) отсутствует, а существует лишь количественное приращение показателя преломления A n , интеграл наложения (5) является не нулевым только в случае, когда а = b , то есть когда падающая и отраженная моды совпадают. Отсюда

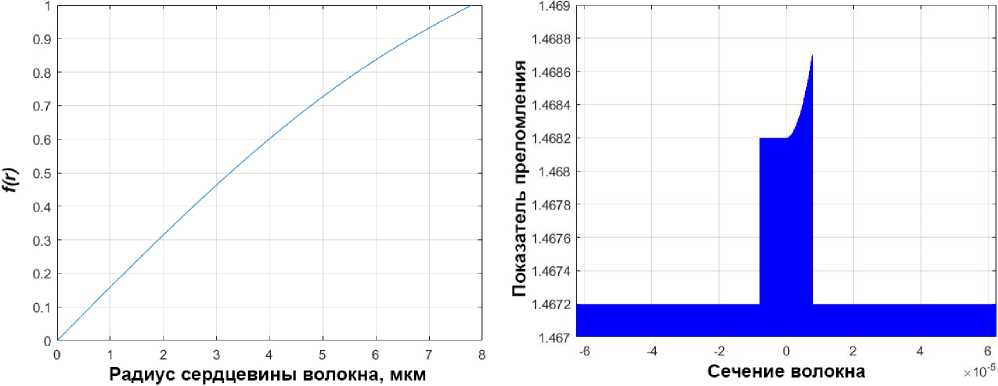
Рис. 5. Профиль ПП сечения ВВБР

Fig. 5. Profile of the refraction index of the section of a chiral fiber Bragg grating

Рис. 4. Вид радиальной функции f ( r ) согласно (8), описывающей поперечный профиль ПП штриха решетки

Fig. 4. The form of the radial function f (r) according to (8), describing the transverse profile of the refraction index of the groove of the grating следует вывод, теоретически подробно обоснованный в [11]: классическая брэгговская решетка не приводит к смешению мод. Однако для конвертирования моды ОУМ0 в моду ОУМ1, очевидно, необходимо, чтобы интеграл наложения между этими модами был ненулевым, а в случае ортонор-мированных сигналов был близок к единице (что означает 100 % перекачку энергии из моды ОУМ0 в моду ОУМ1). Исходя из этих соображений, можно показать, что радиальная функция f(r) будет иметь вид f 1

J111 u 11 r I f (r) — ст—V----Ц,(8)

L JL I

J 011 u01

V где ст - нормирующий коэффициент, а коэффициенты и 01 и и и являются корнями характеристического уравнения для конкретного типа волокна, в котором записывается решетка. На рис. 4 изображен вид функции (8); соответствующий профиль ПП одного штриха ВВБР показан на рис. 5. Данная функция, согласно (6), обеспечивает единичный модуль интеграла наложения.

Учитывая, что величина An порядка должна быть порядка 10-3 (что будет пояснено ниже), можно записать, что n2 ~ n 0 + 2 n о A ne ip° zf (r )eimф,                        (9)

где 5 n2 (r, ф) = 2 n 0 A ne ip0 zf (r )eimф. Тогда выражение (6) можно переписать как kab = i юе0 n 0 A ne i^0 z x

2 n r co .                                                          (10)

x J J e im ^ф f ( r ) E 11 ( r , ф ) ■ E ₀₁( r , ф ) drd ф .

Можно показать, что множитель eimф, описы- вающий геометрическую фазу решетки, обеспечивает ненулевое значение интеграла наложения (10); поскольку последний описывает вероятность перехода фундаментальной моды в моду высшего порядка, данный факт означает возбуждение вихревой моды из LP01. Отметим, что коэффициент отражения w, согласно (4), при аподизации обладает зависимостью от z, т. е. w = w(z). Амплитуду отраженной моды в случае аподизации решетки можно определить как [14]:

L b0 « eiР»L J w(z)e i(p01 P11)zdz,

где коэффициент отражения w ( z ) определяется согласно (4)–(9).

Известно, что показатель преломления определяет вектор электрической индукции, поскольку в случае немагнитных материалов

D — ss ₀ E — n ² s ₀ E.

Задавая n в виде (7), с учетом (9) получим:

^    2   ^

D — n Б 0 E 01 —

= ^e 0

ⁿ 0

I., JL I

J 11 1 u 11 r If

+ 2 n ₀ A ne^^z    ^   r ^{co 2} 2 ^12 e im Ф

| r j J 11 ⁽ u 11 )

J 011 u01

\    rco 22

I,. JL II

J011 u01      |                     J011 u01

V     r^{co 2} p^- i ^e 01 ^{z     2} о V     r^{co 2} p- i ^e 01 ^z ₊

J       \ e =n 0 b0   ,  /

^J 01 ^{( u} 01 )                       ^J 01 ^{( u} 01 )

+ 2 n 0 Б 0 A n

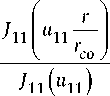
e im Ф e ( P 11 -Ap- 3 p 0 ) z

Рис. 6. Матричная модель нерегулярной ВВБР

Fig. 6. Matrix model of irregular chiral fiber Bragg grating

Распределение интенсивности            Распределение интенсивности падающей моды                     отраженной моды

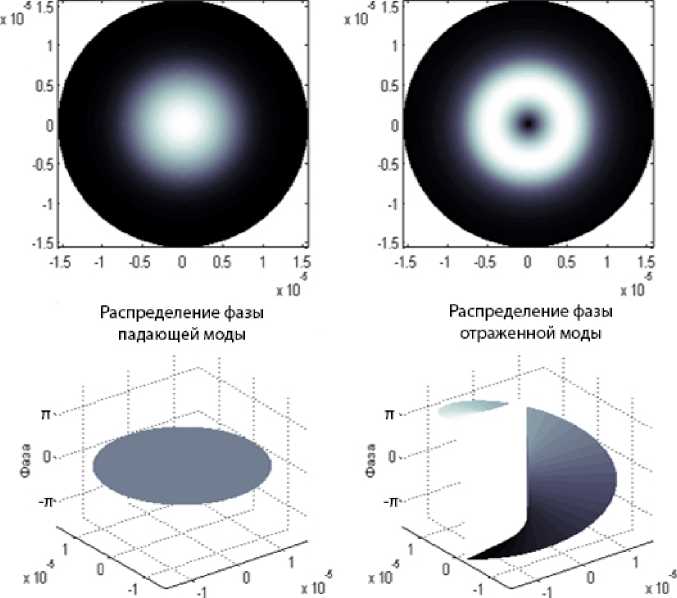
Рис. 7. Отраженное и падающее поле решетки

Fig. 7. Reflected and incident grating field

Как видно из (12), вектор D состоит как из моды ОУМ₀, так и из ОУМ₁-моды. Поскольку в (12) мода i ( р -Ар- 3 р ) z

ОУМ1 имеет множитель e 11     0 , это озна чает, что данная мода будет распространяться навстречу падающей моде ОУМ0.

Матричный подход, рассматриваемый в данной статьи, удобен при анализе нерегулярных и/или каскадных решеток; в таком случае можно разбить сложную решетку на N регулярных участков

(рис. 6), каждый из которых описывается своей матрицей Т_i , а результирующее поле будет иметь вид

^ a 1

. b 1 ,

= T N T T 1

a 0

I b 0

A

Итак, предлагаемая ВВБР предназначена для преобразования падающего поля с плоским волновым фронтом в поле, переносящее ОУМ. На рис. 7 представлены падающее и отраженное поля рассматриваемой решетки.

Анализ рис. 7 позволяет утверждать, что в отраженном излучении формируется вортексная структура поля. Разделить отраженное поле от падающего можно, например, с помощью модового сплиттера.

Согласно выражению (4), можно построить спектр отражения ВВБР, представленный на рис. 8.

Как видно из рис. 8, рассматриваемая решетка обладает коэффициентом отражения порядка R = 0,95 на длине волны 1550 нм, но при этом присутствуют значительные боковые лепестки. При необходимости спектральные характеристики ВВБР можно изменить путем чирпирования или использования функции аподизации.

Поскольку для использования математического аппарата бесселевых функций при описании вортексных мод необходимо оставаться в рамках приближения слабонаправляющего волокна

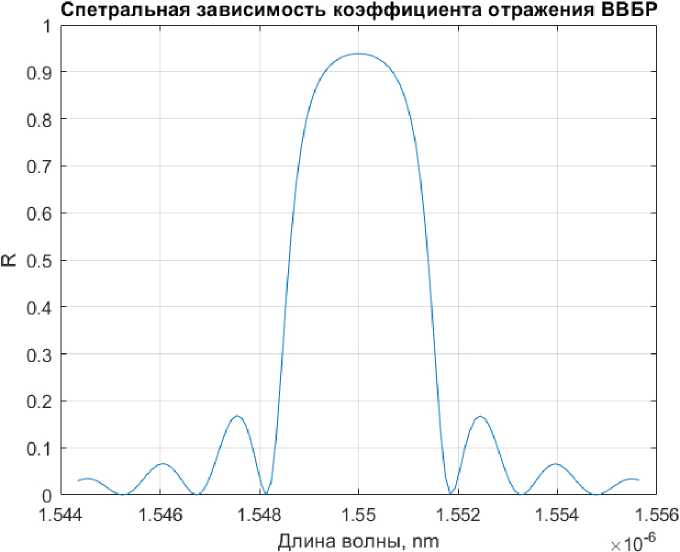
Рис. 8. Спектральная зависимость коэффициента отражения ВВБР

Fig. 8. Spectral dependence of the chiral fiber Bragg grating reflection coefficient

а

б

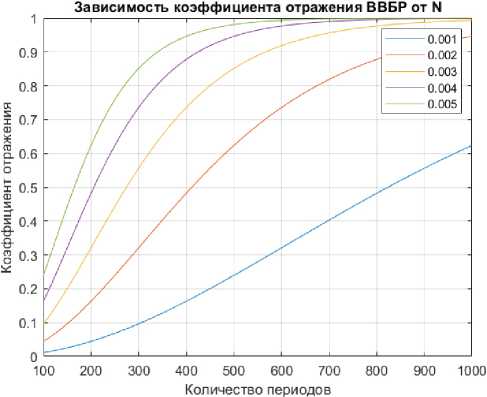
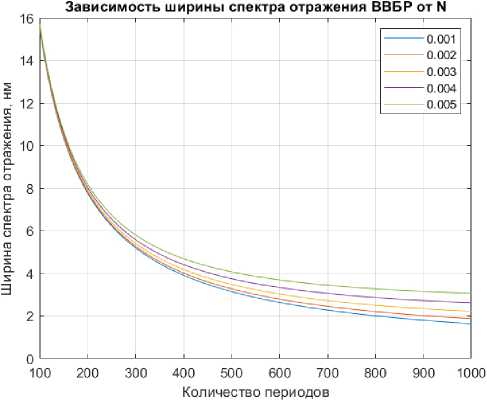
Рис. 9. Зависимость коэффициента отражения ВВБР ( а ) и ширины спектра отражения ( 6 ) от количества периодов (штрихов) решетки при разных значениях амплитуды наведенной модуляции показателя преломления

Fig. 9. Dependence of the chiral fiber Bragg grating reflection coefficient ( a ) and the reflection spectrum width ( b ) on the number of periods (grooves) of the grating at different values of the amplitude of the induced modulation of the refractive index

( △ n < 1 %), амплитуда наведенной модуляции решетки должна быть относительно низкой по сравнению с классическими ВБР (порядка 0,005 для ВВБР против 0,01 для классической ВБР). В связи с этим коэффициент отражения, согласно (4), можно повысить за счет увеличения числа штрихов решетки N . Данная зависимость отображена на рис. 9.

Согласно рис. 9, можно осуществить выбор параметров решетки, например, для заданного зна- чения коэффициента отражения найти значения δn и N, для конкретного значения N подобрать δn и R и т. д. Стоит отметить, что интеграл наложения (10) имеет только фазовый набег e-iβ0z вдоль оси z, при этом модуль интеграла зависит только от поперечных координат. Это означает, что эффективность формирования ОУМ первого порядка из фундаментальной моды не зависит от количества штрихов решетки. Это подтверждается, например, тем, что для формирования вихревого

Длина волны, м

Спектр отражения ВВБР, 5п = 0.005

1.525 1.53 1.535 154 1545 155 1555 156 1565 157 1.575 Длина волны, м               Х1О4

а

б

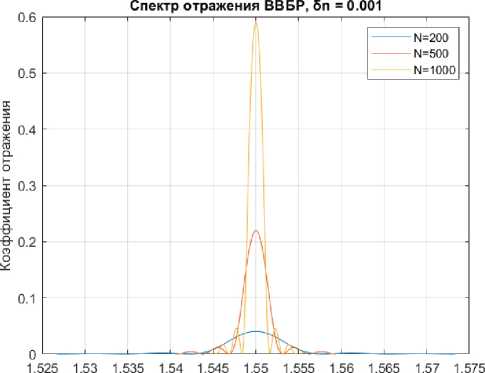
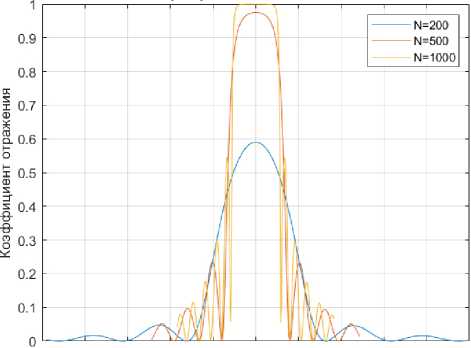
Рис. 10. Зависимость коэффициента отражения ВВБР от количества периодов (штрихов) решетки при разных значениях амплитуды наведенной модуляции показателя преломления: 0,001 ( а ) и 0,005 ( б )

Fig. 10. Dependence of the chiral fiber Bragg grating reflection coefficient on the number of periods (grooves) of the grating at different values of the amplitude of the induced refractive index modulation: 0,001 ( a ) и 0,005 ( b )

радиопучка достаточно одной спиральной фазовой пластины [15], а для формирования оптического вихревого free-space пучка – одиночного ДОЭ. В связи с этим количество штрихов определяет не эффективность формирования ОУМ моды, но эффективность ее отражения, что показано на рис. 10 при различных значениях амплитуды наведенной модуляции показателя преломления и количества штрихов.

Как видно из рис. 10, при δ n = 0,005 уже на значении N = 500 (т. е. 500 периодов решетки) коэффициент отражения составляет порядка 0,97, а двукратное увеличение протяженности решетки теоретически доводит R до единицы. Значение δ n = 0,001 даже при тысяче штрихов решетки обеспечивает лишь 60 % отражения, что говорит об очевидном компромиссе между δ n и N . Как уже упоминалось выше, параметры решетки могут быть рассчитаны, исходя из любых изначальных требований по отражению, протяженности решетки или ширине спектра отражения.

Заключение

Таким образом, в рамках данной статьи предложена математическая модель вихревой брэгговской решетки, основанная на теории смешанных мод и матриц рассеяния. Данная модель позволяет изучить характеристики решетки с произвольными функциями аподизации и чирпирования, с помощью чего можно получить ВВБР с требуемыми спектральными характеристиками, кроме того, рассматриваемая модель позволяет описывать сложные (каскадные) решетки. Предложенная радиальная функция возмущения показателя преломления обеспечивает до 100 % теоретической эффективности формирования ОУМ1 моды из моды ОУМ0. Более того, показано, что, оставаясь в рамках слабонаправляющего приближения, можно добиться сколь угодно высокого коэффициента отражения решетки. Тем не менее вопрос технологии изготовления подобной решетки требует дальнейшего исследования.

Исследование выполнено за счет гранта Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФГБОУ ВО УГАТУ # FEUE-1010-0007 по теме «Теоретические основы моделирования и семантического анализа процессов преобразования вихревых электромагнитных полей в инфокомму-никационных системах».