Формирование параметров модели управления проектом на основе линеаризации функциональных зависимостей

Одним из вызовов четвёртой промышленной революции является требование предоставления продуктов, обладающих ценными для разных целевых групп потребителей свойствами в темпе быстро меняющихся предпочтений. Из этого вытекает необходимость развития теоретических положений, методических и инструментальных средств, предназначенных для предупреждения возникновения и раннего обнаружения в системах управления проектами дефектов разной природы: организационных; технологических; обусловленных психологическими особенностями разработчиков [1-6]. В настоящее время качество информационной поддержки управления становится критическим фактором реализации положений доктрины Индустрия 4.0. Особо значимой становится необходимость совершенствования теоретических положений управления дефектами при реализации аппаратных и программных компонентов цифровой экосреды.

В работе [7] отмечается, что причиной неудачного завершения проектов являлось отсутствие взаимопонимания людей, участвующих и вовлечённых в организацию и реализацию проектов. Получившие в настоящее время широкое распространение методы и модели управления проектами – ISO 21500 [8], ICBIPMA [9], PMBOK PMI [10], НТК СОВНЕТ [11] – предназначены для уровня исполнителей: руководителей проектов, управляющей команды, специалистов. Недостаточно развита методическая и модельная основа поддержки деятельности основных заинтересованных сторон, т.е. уровня принятия стратегических решений. К настоящему времени среди методов поддержки принятия стратегических решений с учётом позиций разных заинтересованных сторон наибольшее распространение получили методы, реализованные в рамках дескриптивного подхода, ограничивающиеся исследованиями на содержательно-описательном уровне. Отмечается необходимость совершенствования обеспечения на основе математических моделей, в том числе моделей со стохастическими параметрами [7].

Анализ источников позволяет утверждать, что наибольшее развитие получили методы выявления дефектов, обусловленных преобразованием функциональных и нефункциональных требований в коды. Эти методы ориентированы на реализацию реактивного подхода к управлению дефектами технологической природы. В то же время, не получили необходимого развития методы проактивного управления дефектами [3, 6, 12], в основе которых лежит предупреждение ошибок системного характера на стадии формирования организационной структуры проекта. Одной из причин возникновения дефектов системного характера в организации проектов является несбалансированность основных характеристик проекта (бюджета, длительности реализации, требований к качеству результатов, в общем случае различающимися у разных целевых групп пользователей). В [13] отмечается, что одним из проявлений несбалансированности характеристик программных проектов является недостаток времени, выделяемого на испытания соответствия потребительских свойств программных компонент информационно-вычислительных систем требованиям технического задания, что является причиной аварий, зачастую имеющих трагические последствия (см., например, [14]).

В настоящей работе рассматривается задача построения формальной модели, являющейся основой формирования сбалансированной системы характеристик проекта, для случая, когда в равной степени важны удовлетворённость свойствами продукта со стороны заказчика и удовлетворённость ходом реализации проекта со стороны исполнителя.

1    Основные допущения предлагаемого подхода

Основу предлагаемого подхода к решению задачи составляют следующие допущения.

• ■    Потребительские свойства конечного продукта определяются организацией и ходом реализации проекта. Основанием этому служат известные утверждения о том, что поведение системы определяется её устройством [15] и, что причинами нежелательных событий, возникающих при управлении сложными субъектоцентрическими системами, являются в первую очередь ошибки в организации управления сложной системой и во вторую очередь - ошибки операторов [4].

• ■    Проект создания сложной системы рассматривается как статический многосвязный объект управления. Это даёт основание рассматривать прямые и перекрёстные связи между входными и выходными параметрами проекта как строгие функциональные зависимости с неизменной структурой и параметрами. Содержание этого допущения является выражением известного положения о взаимовлиянии качества управления проектом и потребительских свойств получаемого продукта (см., например, [16]).

• ■    Программные системы относятся к классу субъектоцентрических систем. При оценивании проектов нужно одновременно использовать как их измерительные данные, так и субъективные оценки потребителей и исполнителей. При оценивании качества хода проекта и потребительских свойств получаемого продукта в равной степени важно учиты-

• вать удовлетворённость исполнителей и заказчиков. В качестве входных параметров проекта рассматриваются бюджет и длительность реализации проекта. В качестве выходных – удовлетворённости представителей заказчика и исполнителей проекта [16, 17].

• ■    Ожидаемый исход проекта в равной мере определяется как ограничениями на бюджет и длительность реализации проекта, так и опытом исполнителя в реализации проектов аналогичного содержания. Содержание этого допущения является выражением известного «принципа ресурсов» [18] и того обстоятельства, что проект сложной системы является разновидностью субъектоцентрических систем [19].

• ■    Допущение о сопоставимости и однородности (в статистическом смысле) исторических данных об основных параметрах проектов и полученных в ходе их реализации продуктов. Основаниями для такого допущения являются то, что организации-разработчики специализируются на реализации проектов в определённой предметной области и то, что внутри организации накапливается опыт решения задач определённой тематической направленности [20], а также то, что ключевые моменты деятельности сотрудников регламентируются стандартами и руководствами.

2    Модель проекта как многосвязного объекта управления 2.1    Структура модели

Проекту, как многосвязному объекту управления, может быть поставлена в соответствие графическая модель, представленная на рисунке 1.

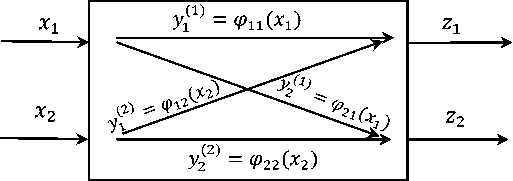
Рисунок 1 – Модель проекта как многосвязного объекта управления

Входными (управляемыми) параметрами модели являются x 1 – бюджет и x 2 – длительность реализации проекта. Выходными параметрами являются удовлетворённость заказчика z 1 и исполнителя z 2 .

Эмпирические функциональные зависимости у⁽ ) = ср tj (xt), ( I, j = 1,2), соответствующие прямым и перекрёстным связям многосвязного объекта, являются строгими. Эмпирические функциональные зависимости строятся на основе измерительных данных и экспертных оценок относительно потребительских свойств созданных продуктов и хода ранее реализованных проектов.

Совместное влияние входных характеристик х^ на выходные определяется на основе функциональных зависимостей, характеризующих прямые и перекрёстные связи у^{( t)} = Фij ⁽х t):

A^(J ) : ^{ y ⁽° = фtj ⁽%t^)} ^ zj = ф <х_г ,Х 2 ),М = ^{1,2 . (1)} Здесь A ( j ) – оператор свёртки, соответствующий j -му выходному параметру модели.

• 2.2    Операторы свёртки

Основу формирования операторов свёртки A( j' ) , преобразующих функциональные зависимости {уу¹) = ф у (Xj)}, характеризующие прямые и перекрёстные связи в зависимости вида zj = Ф_j (х ! , х₂ ),07 = 1,2, составляют следующие положения.

Областью допустимых значений для характеристики удовлетворённости Z j считается интервал Zj Е [0,1], ]' = 1,2. Нижняя граница интервала соответствует варианту, когда субъекты (потребитель/исполнитель) абсолютно не удовлетворены результатами/ходом проекта. Верхняя граница интервала соответствует их абсолютной удовлетворённости.

Удовлетворённость потребителя уменьшается по мере увеличения как бюджета x 1 , так и длительности реализации проекта x ₂. Поэтому функциональные зависимости у^ ) = ф jj (х^) являются обратными. При этом возможна компенсация одного параметра другим. К примеру, компенсация изменения длительности реализации проекта за счёт изменения бюджета проекта и наоборот [13].

С точки зрения заказчика возможна реализация проекта нулевой длительности, что фактически соответствует приобретению готового продукта. Исходя из изложенного выше, можно утверждать, что Ф 1 ( x 1 , x ₂) можно представить аддитивной функцией, т.е.

Z 1 = Ф 11 UJ + Ф 21 (* 2 ) (2)

Удовлетворённость исполнителей, напротив, растёт с увеличением как бюджета x 1 , так и длительности реализации x 2 проекта. Постулируется, что исполнитель отказывается от реализации проекта, если хотя бы одна из его характеристик x i ( i = 1, 2) равна нулю.

Исходя из этих соображений можно заключить, что в качестве Ф₂( x 1 , x ₂) можно использовать:

Z 2 = ф 12 U1 ) * Ф 22 (* 2 ) (3) т.е. мультипликативную функцию.

3    Постановка и схема решения задачи

Известен вид функциональных зависимостей у^) = фjj (х j ), i , j = 1, 2.

Требуется оценить значения параметров проекта xi ⁽ OU^{T )} ( i = 1, 2), при которых достигается наименьшее различие в удовлетворённости результатами проекта потребителей z 1 и исполнителей z 2 .

Очевидно, что наименьшее различие в удовлетворённости результатами проекта потребителями и ходом проекта исполнителями достигается при z 1 = z2. Этому условию соответствует соотношение ф 12 U1 ) * Ф22 (*2 ) = Ф11 U1 ) + Ф21 (*2 )

При этом должны соблюдаться ограничения:

0 < ф 11 (Х1) + ф21 (Х2) < 1,

0 < Ф12 U1 ) * Ф2 2 (Х ) < 1,

Х > 0,i = 1,2.(7)

Вначале рассмотрен случай, когда прямые и перекрёстные связи представляются линейными зависимостями. При этом критичность величины бюджета и длительности реализации проекта для заказчика характеризуются параметрами а_{г г} и а _{2 г}, а предыдущий опыт реализации проектов исполнителями характеризуется параметрами b_{г 2} и b ₂₂ .

Совокупное влияние х । , х₂ на z 1 , z₂ определяется соотношениями:

^Z1 = ⁽ Cl 01 - ^d1 1 ^X1 ) + ⁽ d o2 - ^d21 ^X2 ),                              (8)

Z₂ = Ь 12 X_t*2) 2 2 X 2 .                                       (9)

Предполагая равное влияние бюджета и длительности реализации проекта на удовлетворённость заказчика, а также то, что при х ₁ = х ₂= 0 (результат получается моментально и даром) удовлетворённость заказчика максимальна, получаем а ₀₁ = а ₀₂ = 0,5 .

Тогда

Z1 = 1-111 X1—d2 1 X2,(10)

Z2 = 1122 X1 * 122 X2 = ВX1X2.

С учётом того, что Zj < 1, из (10) и (11) получаем х2 > 1 а 1 1 х 1 = с — ^ 1,(12)

а21

X2 < х, где С =—, е = —, к = -. а21      а215

Соотношения (12) и (13) определяют область, в которой возможен поиск х^{(0 тт}^ и х^{(0 ТТ}\ Эта область на рисунке 2 выделена штриховкой.

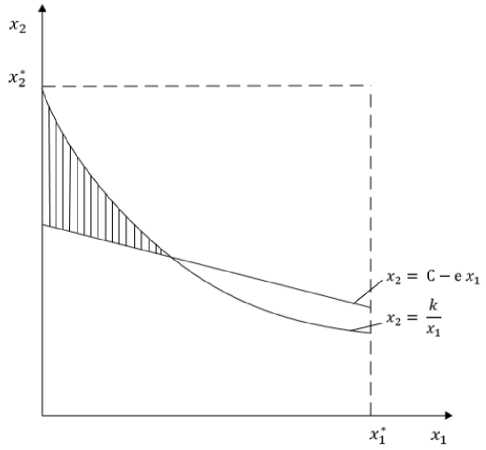
Рисунок 2 - Область поиска х^{(0 тт}\ i = 1,2

На основании полученных зависимостей с учётом реальных ограничений на бюджет x ₁ * и длительность реализации проекта x ₂ на ранних стадиях проекта можно оценить предполагаемое качество результатов с учётом опыта взаимодействия исполнителя и заказчика.

На рисунках 3-5 приведены примеры результатов оценки, соответствующие различным представлениям о ценностях заказчика и исполнителя.

На рисунке 3 значения параметров соответствуют случаю, когда удовлетворённость заказчика определяется длительностью реализации проекта и практически не зависит от величины бюджета проекта. Удовлетворённость исполнителя определяется как величиной бюджета проекта, так и длительностью реализации проекта. Содержательно такая ситуация может иметь место при обеспечении информационной поддержки ликвидации последствий чрезвычайной ситуации, когда в качестве заказчика на информационное обслуживание выступают органы исполнительной власти, а исполнителями - научно-производственные организации, являющиеся структурными подразделениями этих органов.

Рисунок 5

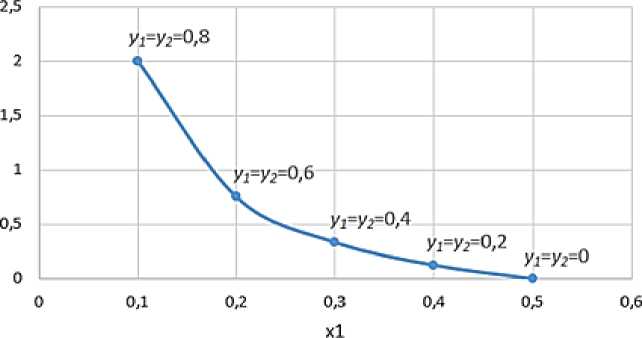
—•—311=2, 312=0, Ь22=Ы2=2

Рисунок 3 - Пример зависимости степени удовлетворённости от х^{(0 ит}\ i = 1,2

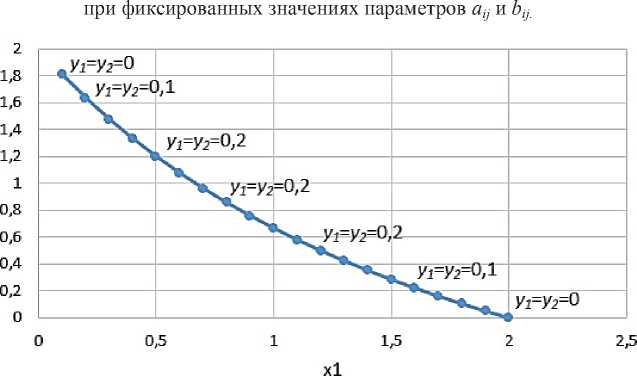
• а 11=321=0,5, Ь22=Ь 12=0,5

Рисунок 4 - Пример равного влияния бюджета и длительности реализации проекта

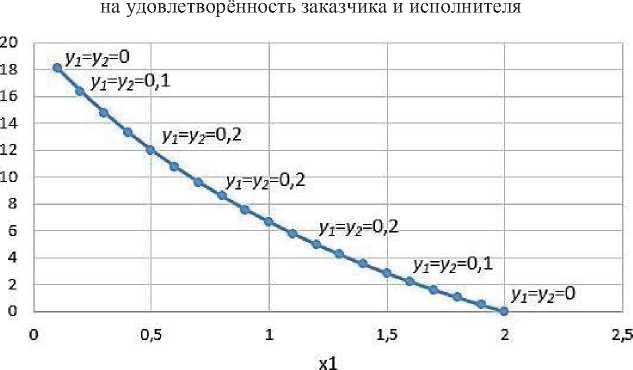
• 311=0,5, 321=0,05, Ь22=0,05, Ы2=0,5

Пример важности значения величины бюджета проекта по сравнению со сроками его реализации

4    Квантификация экспертных оценок

Организация проектов относится к классу задач управления субъектоцентрическими системами. Это означает, что характеристики проекта в значительной степени определяются субъективными решениями, принимаемыми разработчиками и пользователями. К субъективным оценкам относятся, в частности, удовлетворённость пользователей потребительскими свойствами продукта, а также хода реализации проекта исполнителями. В силу этого при построении математических моделей проекта как многосвязного объекта управления возникает потребность в количественном выражении субъективных оценок пользовате-лей/разработчиков. Основу предложенного подхода составляет адаптация известного аппарата лингвистических шкал и функций принадлежности, применительно к задаче количественного оценивания удовлетворённости субъектов.

Пусть удовлетворённость субъектов изменяется в диапазоне z е [0; 1]. Удовлетворённость тем ниже, чем ближе значение z к нижней границе интервала, и наоборот. Нуль соответствует абсолютной неудовлетворённости; единица - абсолютной удовлетворённости.

Пусть известна заранее сформулированная в терминах лингвистическая шкала, которой пользователи, принадлежащие к одной и той же m -й целевой группе, оценивают свою удовлетворённость потребительскими свойствами продукта. Пусть для определённости эта шкала имеет вид {низкая; средняя; высокая}.

Постулируется, что оценки, даваемые пользователями, отражают их истинное независимое мнение относительно свойств продукта и на них не влияет, например, принадлежность к какому-либо альянсу [21].

Каждому l -му значению лингвистической шкалы ставится в соответствие функция принадлежности , определённая на интервале ∈ [0;1] Положение максимума принадлежности l -го значения лингвистической шкалы определяется как его опорное значение r _l на оси у (рисунок 6). На рисунке 6 {г_г^(н),г_г^(в)} - нижняя и верхняя границы, в которых на оси у определена l -я функция принадлежности.

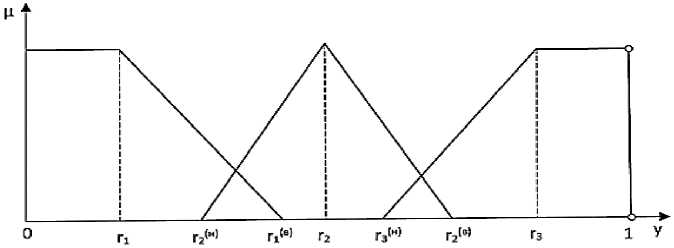
Рисунок 6 - Качественный вид функции принадлежности лингвистической шкалы

В терминах лингвистической шкалы пользователи выражают степень своей удовлетворённости потребительскими свойствами продукта. Помимо этого, каждый к-й пользователь характеризует свою уверенность в даваемой оценке, выражаемой числом рк £ [0,1]. В результате пользователями, принадлежащими одной целевой группе, потребительским свой- ствам продукта ставится в соответствие оценка вида:

Е^(т^ =

yNт „ СО^СУ

∑       ∗

Y^ тп, ., (0   '

∑

где N_m - количество пользователей, принадлежащих m -й целевой группе; гр^ - опорное значение, соответствующее l -му значению лингвистической шкалы, определённому к -м пользователем; р^ - степень уверенности к -го пользователя в даваемой оценке.

В качестве совокупной оценки степени удовлетворённости выбирается опорное значение r l , наиболее близкое к E m . Степень уверенности в полученной оценке определяется как Нт (Е^(т)).

Основными неопределённостями, затрудняющими практическое использование (14), является выбор:

■

■

■

значений r ;

формы функции принадлежности ^ г; например, в [22] приведено описание большого числа функций принадлежности разной формы, однако не определены практические рекомендации по их применению;

значений границ {г ^(н\ г_г^(в)}.

Для устранения выделенных неопределённостей предлагается использовать следующее.

В основу определения r l положить учёт доли пользователей, принадлежащих m -й целевой группе и выбравших l -е значение лингвистической шкалы.

При таком подходе в качестве r 1 выступает величина п^(т)/М _т, где п^ ) - число пользователей m -й целевой группы, выбравших значение лингвистической шкалы «низкая».

В качестве r2 выступает величина г = £)+£ ^т 2№т

где п(т)- число пользователей целевой группы, выбравших значение лингвистической шкалы «средняя».

Значение r ₃ определяется соотношением

„*

3                                '

Величина r ₂, определяемая соотношением (15), представляет собой середину подинтервала между значениями r 1 и r 3 .

Относительно неопределённостей, связанных с выбором формы функции принадлежности, а также нижней и верхней границ {г ^(н\ г ( ^в)}, необходимо отметить следующее.

Если значению r 1 соответствует максимальное значение лингвистической шкалы «низкая», то левее r 1 степень удовлетворённости увеличиться не может, т.е. ц_г при у е [0; r 1 ] принимает значение 1. Правее точки r 1 уверенность эксперта в выбранной оценке падает. В силу того, что какие-либо сведения о скорости уменьшения значения ц_г по мере удаления вправо от точки r 1 отсутствуют, следуя принципу максимизации энтропии [23] целесообразно считать эту скорость постоянной.

В силу отсутствия сведений, накладывающих ограничения на область определения , в качестве такой области целесообразно принять весь интервал у е [ r 1 ; 1].

С учётом высказанных соображений ц_г принимает вид, представленный на рисунке 7. Рассуждая по аналогии, функции принадлежности для выбранной лингвистической шкалы имеют вид, представленный на рисунке 8.

Пример использования предлагаемого подхода для квантификации экспертных оценок.

Пусть в результате опроса десяти пользователей, принадлежащих одной и той же целевой группе, получены следующие оценки потребительских свойств продукта и степень уверенности в даваемых оценках: {низкая, 0.8};{средняя, 0.95};{средняя, 0.7};{высокая, 0.4};{средняя, 0.8};{низкая, 0.7};{средняя, 0.8};{средняя, 0.6};{высокая, 0.7};{высокая, 0.9}.

В соответствии с (14) значение Е ^m) составит:

, ,   0,2(0,8 + 0,7) + 0,45(0,95 + 0,7 + 0,8 + 0,8 + 0,6) + 0,3(0,4 + 0,7 + 0,9)

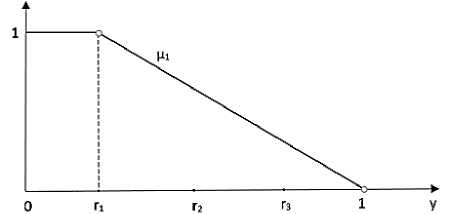
Рисунок 7 - Вид функции принадлежности ц 1

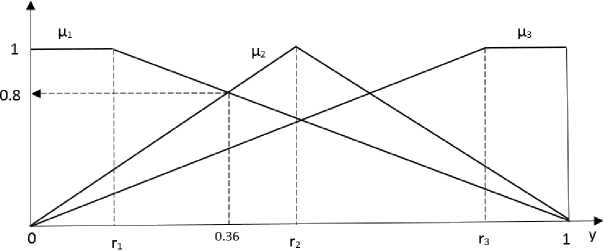
Рисунок 8 - Итоговая форма функций принадлежности лингвистической шкалы

Ближайшим опорным значением к Е^ оказывается r 2 = 0,45. Значению Е^(т^ соответствует значение [л_т(0,36) = 0,8 (см. рисунок 8).

Интегральной характеристикой удовлетворённости свойствами продукта всех целевых групп пользователей в рамках описываемого подхода может выступает показатель

₇ _ 2%=i E ^{(m )}^m

=   vM

∑ где Е(т) - характеристика степени удовлетворенности m-й целевой группы пользователей; [лт - степень уверенности в даваемой оценке.

Аналогичный подход может использоваться для исследования степени удовлетворенности ходом проекта различных профессиональных групп разработчиков и команды проекта в целом. Предлагаемый подход к квантификации экспертных оценок является в значительной степени формализованным, что позволяет реализовать его в качестве функциональной компоненты в системах поддержки принятий решений.

Заключение

Рассмотренный подход делает возможным оценить предполагаемую удовлетворённость заказчика результатами проекта, а исполнителей - ходом проекта в зависимости от бюджета и ограничений на длительность проекта c учётом опыта, полученного от ранее реализованных проектов. Предложенная формальная модель проекта, как многосвязного объекта управления, даёт возможность повысить обоснованность принятия стратегических решений по организации проекта основными заинтересованными сторонами. Ограничениями модели являются: линейный характер функциональных зависимостей, характеризующих прямые и перекрёстные связи; предположение о равных приоритетах интересов заказчика и исполнителя.

Исследования выполнены при поддержке гранта РФФИ №19-08-00937 А «Методы и модели интеллектуальной поддержки принятия решений при управлении программными проектами, реализуемыми в среде производственных предприятий».