Формирование полного набора скелетонов произвольного контура

Введение. В задачах распознавания образов использование процессов сжатия информации имеет большое значение как для ускорения процессов распознавания, так и для повышения надёжности распознавания.

Одним из методов, активно использующих процесс сжатия, является метод скелетонов [1, 2]. Использование скелетонов при обработке текстовой информации избавляет от настройки на конкретный вид шрифта и, таким образом, повышает качество автоматического анализа текстов. В публикациях приводятся разные алгоритмы построения скелетонов, но все они трудоёмки, и их реализация на компьютере требует много времени [2].

Предлагаемый алгоритм построения комплекса скелетонов позволяет уменьшить трудоёмкость этого шага распознавания. Основной функцией представленного алгоритма является построение главной (стержневой) составляющей набора скелетонов произвольного контура, на базе которой последовательно один за другим строятся остальные скелетоны.

Алгоритм. По алгоритму на первом этапе строится последовательность кругов различных радиусов, вписываемых в произвольный контур, а на втором этапе строится весь комплекс скелетонов.

На первом этапе контур разбивается на фрагменты. Каждый фрагмент представляет собой «многогранник» со сторонами, образуемыми отрезками прямых или кривых. Основное свойство таких фрагментов заключается в том, что в них можно вписать круг так, что площади, принадлежащие фрагменту, но лежащие вне круга, могут использоваться на следующих шагах алгоритма. На рис.1 показан произвольный контур, который разбивается на фрагменты для вписывания кругов 1-го уровня.

Рис. 1. Разбиение контура на фрагменты для формирования кругов 1-го уровня

Незанятые площади внутри контура не заштрихованы. Жирными линиями дан вариант рассечения площади внутри контура на фрагменты. На сторонах фрагмента выбираются две-три любые точки, которых касается вписанный круг.

Разбивая на фрагменты всю площадь, ограниченную контуром, получаем последовательность кругов, заполняющих всю площадь, ограниченную контуром, которую назовём кругами 1-го уровня. Построение последовательности этих кругов может быть реализовано не единственным образом, однако для формирования комплекса скелетонов это не имеет принципиального значения.

Для построения кругов 2-го уровня необходимо использовать площади фрагментов, не занятые кругами предыдущих уровней. В незанятые площади контура вписываются круги следующих уровней (рис.2).

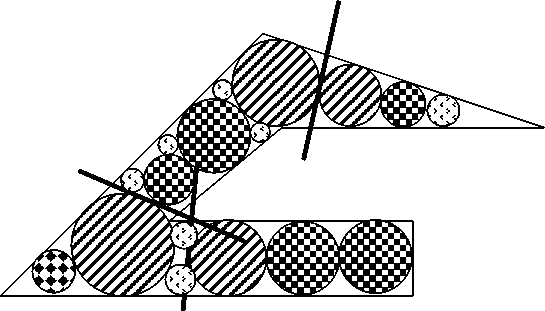
Рис. 2. Формирование окружностей следующих двух уровней

Процесс вписывания кругов продолжается до тех пор, пока площадь, не вошедшая в круги всех уровней, не станет меньше заданной величины – погрешности построения данного набора скелетонов.

На втором этапе соединяются центры кругов 1-го уровня отрезками прямых линий (рис.3).

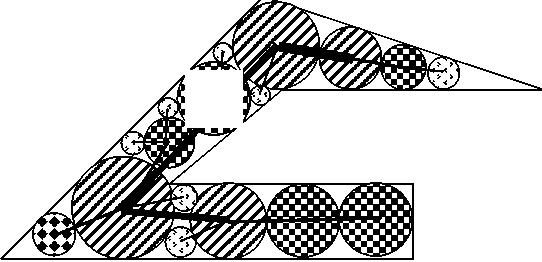
Рис. 3. Построение стержневой составляющей и «боковых» компонентов набора скелетонов

Набор этих отрезков образует стержневую составляющую. К стержневой составляющей добавляют «боковые», последовательно соединяя любой центр круга, входящего в последовательность кругов 1-го уровня, и центр ближайшего круга 2-го уровня, затем любой центр круга

2-го уровня, и центр ближайшего круга 3-го уровня и так далее. В тех случаях, когда есть необходимость ограничить число скелетонов, процесс можно остановить на любом уровне.

Выводы. Предложенный метод построения полного набора скелетонов сходится в любом случае, так как площадь, ограниченная контуром конечна, и в зависимости от критерия остановки процесса полный набор скелетонов будет получен. Следовательно, процесс сходится к решению не зависимо от последовательности построения кругов соответствующих уровней.

Описанный метод построения скелетонов может найти применение при решении таких задач, как обработка текстовых документов, сжатие растровых графических изображений, представленных в виде набора контуров, распознавание автомобильных номеров, взятых с камер слежения, определение группы крови, построение рационального расположения штреков шахты по известному контуру залегания угля и другие.