Формирование пространственно-временных структур и хаотических режимов ансамблем автогенераторов в двумерном волновом поле

Исследования, направленные на изучение колебаний в активных распределенных системах при наличии активных элементов, представляют интерес для различных прикладных задач [1]. Эффективным методом исследования динамики нелинейных систем различной природы является построение численных моделей. При этом наряду с моделями, разработанными для расчета конкретных систем, представляют интерес достаточно абстрактные модели для исследования общих закономерностей [2; 3].

Цель работы – исследование образования пространственно-временных структур и режимов динамического хаоса в процессе самосогласованного взаимодействия ансамбля активных осцил- ляторов с волновым полем.

Дискретная модель волнового поля представ- ляет собой двумерную решетку связанных осцилляторов. Динамика решетки описывается си- стемой уравнений в конечных разностях:

u ( x , y, t + 1) = a y u ( x , y, t ) - a 2 u ( x , y, t - 1) + + bW ( t , x ± 1, y ± 1) + gF ( x, y, t ),

где

W ( x ± 1, y ± 1, t ) = u ( x - 1, y, t ) + u ( x + 1, y, t ) + + u ( x, y - 1, t ) + u ( x , y + 1, t );

u(x, y, t) – функция дискретных аргументов, из- меняющихся с единичным шагом, определяющая состояние поля в точке с координатами x, y в момент времени t; g – коэффициент связи волнового поля с автогенераторами; F(x, y, t) – функция, описывающая действие осцилляторов на поле:

N

F ( x , y, t ) = ^ 8 ( x - x ( n )) 5 ( y - y ( n )) A z ( n , t ),      (2)

n = 1

где A z ( n , t ) = z ( n , t ) - z ( n , t - 1),

5 ( 8 ) =

1, 8 = 0,

0, 8 ^ 0,

z ( n , t ) описывает состояние осциллятора в точке с координатами x ( n ), y ( n ) в момент времени t .

Коэффициенты a ₁ и a ₂ уравнения (1) имеют следующий вид:

a1 = 2(2v2 - 1) exp(-y), a 2 = exp(-2y),                                    (3)

b = v2 exp(-y), где v — фазовая скорость волны; у — декремент затухания.

Волновое поле, описываемое уравнением (1), представляет собой решетку осцилляторов. Пространственные координаты изменяются в области 0 <  x <  L , 0 <  y <  H причем ( L >  H ). Для продольной координаты x было принято периодическое условие u (0, y ) = u ( L , y ). Верхняя граница волнового поля подвергается модуляции следующим образом:

f (x) = A cos4(nx / X), в общем случае для нее приняты нулевые граничные условия u(x, H, t) = 0. Для нижней границы: u(x, 0, t) = u(x, 1, t). При этом длина волны

модуляции границы кратна длине области по оси x , L = K b X . Данные ограничения позволяют представить область волнового поля в виде боковой поверхности цилиндра с высотой H .

Динамика осциллятора, взаимодействующего с полем в точке с координатами x(n), y(n), опи- сывается уравнением:

z ( n , t + 1) = d y (z ) z ( n , t ) -

- d 2 ( z ) z ( n , t - 1) + g A u ( x ( n ), y ( n ), t ),

где

A u ( x ( n ), y ( n ), t ) =

= u ( x ( n ), y ( n ), t ) - u ( x ( n ), y ( n ), t - 1).

Коэффициенты d ₁ и d ₂ этого уравнения нелинейно зависят от состояния осциллятора:

d1 = 2 exp(s(1 - az2(n, t))) cos(P), d2 = exp(2s(1 - az2(n, t))).

При малой нелинейности параметров б <<  1, sa <<  1 уравнение (4) переходит в дискретную модификацию уравнения Ван-дер-Поля, рассмотренную в [4]. Параметр в определяет частоту колебаний осциллятора.

Частоты мод волнового поля в области без мо- дуляции границ определяются из решения краевой задачи для волнового уравнения с непрерывными координатами следующим образом:

в n . m = v(2 п n / L )² + ( п (2 m + 1) / H )².

Зависимость (n, m) – моды от пространствен- ных переменных – имеет следующий вид:

u n . m ^{( x} , ^y )

2     . ( 2 n )

.---sin nx X

V LH   I L )

( n x sin     (2m + 1)y

I 2 H

Ансамбль автогенераторов представляет собой фиксированный набор N_s -сгустков, содержащих N_b -осцилляторы. Такой набор был расположен

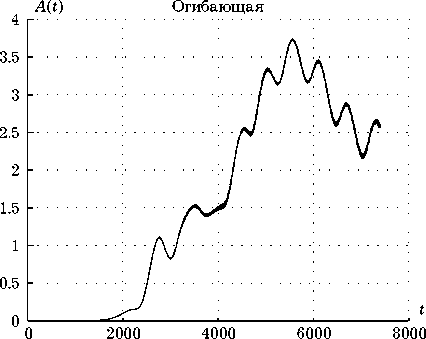
Рис. 2

n               .1

—^{(2 m} + 1) y I .

2 h         ;

-10

-20

-30

-40

-50

-60

-70

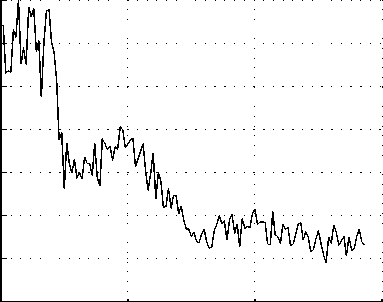
S x ( n )           Спектр поля

0               50              100             150

Рис. 5

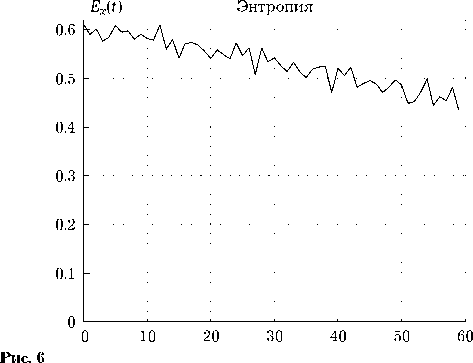
рить о наличии режима динамического хаоса, имеет значение E ≈ 0.5.

Анализ спектральных характеристик колебаний проводился по реализации функции u ( x_i , y , t ), где y = H - 2, i = 1, 2,..., M_t , где M_t = 21. Записи состояния поля по времени объема V_t проводили в интервале T - V_t , T , где T – полное время вычисления эволюции системы. По спектрам M_t реализаций S_{t , i} ( n ) находили реализацию с максимальной мощностью:

P t

1 max 1 ≤ i ≤ M t ( V_t - 1)²

V t - 1

∑ S_{t , i} ( n ).

n = 1

Спектральные свойства волнового режима St (n) определяла спектральная плотность этой реализации. Номер гармоники с максимальным значением спектра nmax определял частоту колебаний β=2πn/V.

u max t

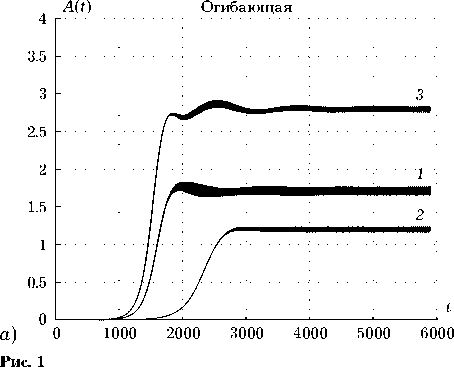
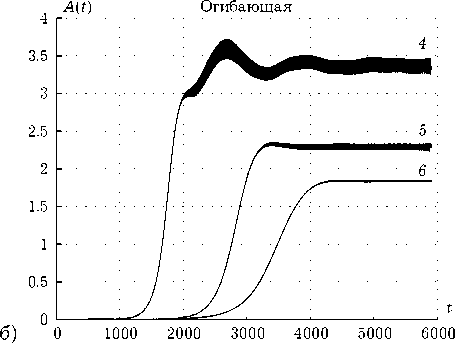
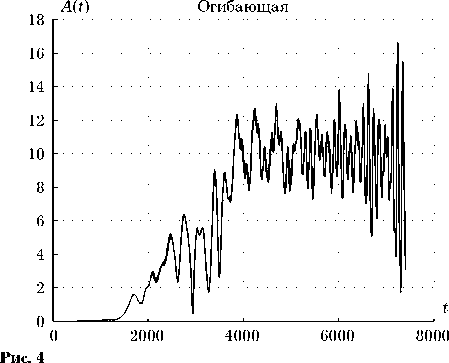
Приведенные ниже результаты получены при постоянном значении скорости волны v = 0.7 и значений параметров осцилляторов ε = 0.001, α =0.7. На верхней границе поля отсутствовала модуляция (A = 0). Значения варьируемых параметров приведены в табл. 1. На рис. 1 изобра- жены графики амплитудных огибающих данной серии.

Как мы видим, набольшую амплитуду, при сохранности структуры имеет волновой режим 5.

Рассмотрим процесс перехода системы от устойчивых колебаний к режиму динамического хаоса. Запишем функцию ∆ u из уравнения (4) в виде:

∆ u ( x ( n ), y ( n ), t ) = u ( x ( n ), y ( n ), t ) -- u ( x ( n - 1), y ( n - 1), t - 1).

Для волнового режима 5 модифицируем воздействие поля на осцилляторы согласно (6).

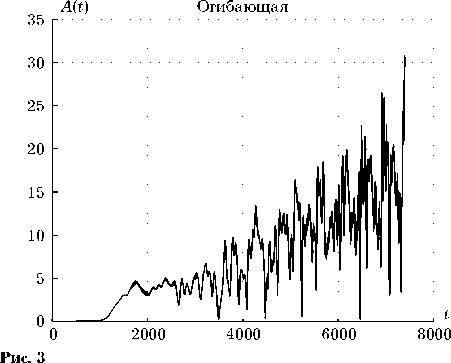
Полученный колебательный режим, представленный на рис. 2, показывает, что уравнение (6) разрушает полученную структуру. Усилим этот процесс и увеличим коэффициент связи между полем и осцилляторами g = 0.09. Получим колебания, изображенные на рис. 3. Данный процесс не является стационарным, поэтому не могут быть надежно оценены его спектральные характеристики и энтропия.

В работе [6] делается вывод о возможности применения модуляции границы двумерного волнового поля для снижения пространственной регулярности волнового режима. Однако модуляция границы также участвует в формировании стационарного процесса. Для варианта, полученного на рис. 3, введем модуляцию верхней границы поля A = 10. Амплитудная огибающая полученного режима представлена на рис. 4. Таблица 2 демонстрирует параметры данного колебательного режима. Видно, что пространственная энтропия полученного режима удовлетворяет заявленному параметру E ® 0.5. На рис. 5 и 6 изображены его пространственный спектр и энтропия соответственно.

Сравнение колебательных режимов, образующих пространственно-временные структуры, показывает, что на основе (2) невозможно получить режим колебаний такой же высокой амплитуды, как режим в [6]. Предложенный способ перехода системы к хаотическому режиму, может быть использован для получения хаотических сигналов с различными конфигурациями спектра и энтропии. Полученный хаотический режим можем быть использован в методах маскировки информации [7].

Таблица 1

	1	2	3	4	5	6
g	0.12	0.08	0.09	0.08	0.05	0.03
Nx	5	5	8	10	10	15
N y	5	5	8	10	10	15

Таблица 2

ResBet	betF	Entr	Power	VonA	spEntr	saPower
0.2000	0.2420	0.7042	49.0691	11.0000	0.5316	186.3251