Формирование регулятивных универсальных учебных действий у младших школьников на уроках математики

Приоритетной целью школьного образования, в соответствии с Федеральным государственным образовательным стандартом начального общего образования (ФГОС НОО), являются умения учащихся самостоятельно ставить учебные цели, проектировать пути их реализации, контролировать и оценивать свои достижения [8]. Все перечисленные умения можно выразить несколькими словами «умение учиться». Поставленная цель образования может быть реализована благодаря формированию регулятивных универсальных учебных действий, обеспечивающих возможность управления познавательной и учебной деятельностью [6].

С целью выявления сформированности регулятивных универсальных учебных действий, учащимся 4 «А» класса (21 ученик) МКОУ «Основная школа № 4 имени Ю.А. Гагарина» городского округа город Фролово, обучающимся по программе «Школа России» (авторы учебников по математике: М.И. Моро, С.И. Волкова, С.В. Степанова) [5] были предложены задания, которые позволили сделать следующие выводы:

• -    5 человек планируют свои действия в соответствии с поставленной задачей и условиями её реализации; осуществляют итоговый и пошаговый контроль по результату; прогнозируют, умеют рассуждать, переносить общие суждения на частные (высокий уровень);

• -    7 человек планируют свои действия в соответствии с поставленной задачей и условиями её реализации, однако не всегда безошибочно осуществляют итоговый и пошаговый контроль по результату, допускают ошибки при выстраивании цепочки рассуждений (средний уровень);

• -    9 человек, планируя свои действия в соответствии с поставленной задачей и условиями её реализации, допускают ошибки, либо не могут планировать, не могут осуществлять итого-

• вый и пошаговый контроль по результату, не умеют выстраивать цепочку рассуждений (низкий уровень).

На наш взгляд, такие действия, как целеполагание; планирование; прогнозирование; контроль в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона; коррекция; оценка; волевая саморегуляция, – все это возможно сформировать с помощью включения в учебный процесс алгоритмов или заданий алгоритмического характера. Выполняя такие задания, учащиеся могут организовать их выполнение рационально не только с помощью поддержки учителя, но и самостоятельно.

Вопрос о возможности использования алгоритмов с целью формирования регулятивных универсальных учебных действий в начальной школе до настоящего времени мало изучен.

Проведенный нами анализ на выявление алгоритмов в образовательной программе «Школа России» позволил выявить, что само понятие «алгоритм» знакомо учащимся. При выполнении сложения, вычитания, умножения и деления натуральных чисел, записывается алгоритм и одновременно показывается его выполнение на примерах; в учебниках на полях учащимся предлагается рассмотреть рисунок, на котором изображена цепочка, для выполнения арифметических действий.

Необходимо отметить, что в 1–2 классах рассматриваются цепочки с уже готовым результатом, а в 3–4 классах предлагается самостоятельно найти значение. В учебниках представлены странички для любознательных. На одной из таких страничек (3 класс) показана работа вычислительной машины, в виде разветвляющегося алгоритма, заданного с помощью блок-схемы.

Возможности повышения алгоритмической культуры младших школьников, способствующей улучшению качества обучения, отражены в ряде научных работ таких исследователей, как М.Н. Грабарь, В.Г. Житомирского, В.М. Завырыкина, Т.А. Ильиной, К.А. Краснянской, Ж.Н. Тельновой [1, 2, 3, 7].

В данных исследованиях также показаны пути соответствующей подготовки учителей начальных классов. Однако, в работах перечисленных авторов не идет речь о развивающих возможностях алгоритмов, о дидактических условиях, технологиях, которые смогли бы повысить эффективность образовательного процесса [4, c. 104].

Нами был подобран комплекс заданий на формирование у обучающихся регулятивных универсальных учебных действий в соответствии с требованиями ФГОС НОО [8] с использованием алгоритмов разных видов: линейные, с ветвлением (разветвляющиеся), циклические, заданные словесно или с помощью блок-схемы.

На начальном этапе работы с алгоритмами учащимся предлагались небольшие линейные (словесные) алгоритмы и предписания алгоритмического типа с постепенным свертыванием шагов и усложнением заданий на следующих этапах.

Задание 1. Тема: «Нумерация».

• 1.    Постройте числовой луч. Опишите подробно шаги, которые будете для этого выполнять.

• 2.    Прочитайте и сравните алгоритм, который составила ученица Валя с вашим:

• 1)    необходимо поставить точку и провести от нее вправо луч;

• 2)    у начальной точки луча необходимо поставить число 0;

• 3)    выбрать мерку и отложить ее от начальной точки луча вправо;

• 4)    поставить у конца отложенной мерки число 1.

• 5)    отметить заданные числа.

• 3.    Сравните составленный вами алгоритм с алгоритмом, записанном на доске.

Задание 2. Тема: «Величины».

Каждому ученику предлагался алгоритм «Вычисление площади фигуры с помощью палетки» (см. рис. 1 на с. 9).

Наложить палетку на фигуру

Сосчитать число а целых клеток внутри фигуры

Сосчитать число b клеток входящих в фигуру частично ;

Сосчитать приближенное значение площади S ~ а + b : 2 (если число b нечетное, то увеличить его на 1)

Рис. 1. Алгоритм вычисления площади фигуры

После прочтения алгоритма учащимся необходимо было выполнить следующее задание: «Вычислите приблизительную площадь данных фигур» (см. рис. 2).

Рис. 2. Изображение фигур

Задание 3. Тема: «Деление на однозначное число».

Выполните задание по приведенной ниже блок-схеме (см. рис. 3), подставив значения (числа): 40; 130; 640. Результаты вычислений запишите в табл. 1 на с. 10.

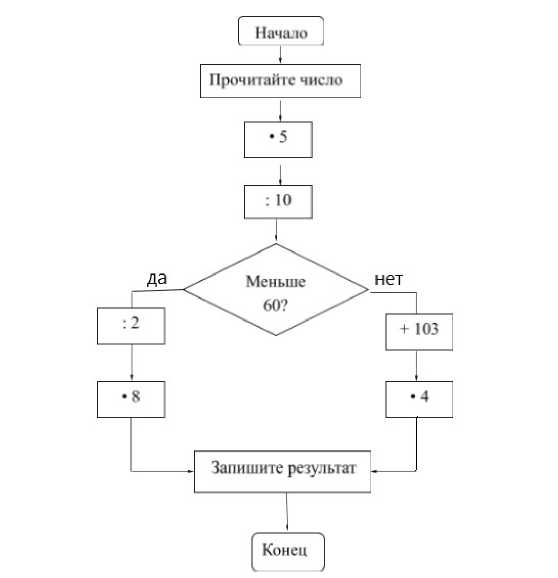
Рис. 3. Алгоритм

Таблица 1

Таблица данных

Число	40	130	640
Результат	?	?	?

Постепенно задания усложнялись. Учащимся предлагались алгоритмы с «ловушками», алгоритмы, которые носили интегрированный характер.

Задание 4. Тема: «Деление на однозначное число».

Пользуясь заданным алгоритмом (см. рис. 4), подставьте значение числа «a», используя табл. 2, найдите значение ‘х’ и запишите результаты вычислений.

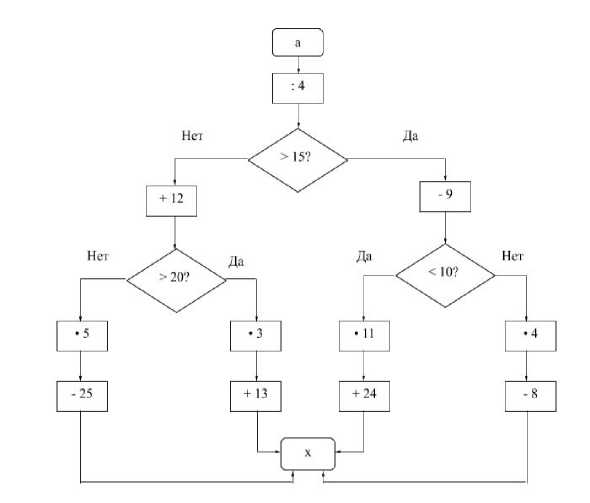
Рис. 4. Алгоритм

Таблица 2

Таблица данных

Число a	4	20	32	48	64	80	100
Результат х	?	?	?	?	?	?	?

После заполнения табл. 2 сопоставьте полученное значение и соответствующую букву, используя табл. 3.

Таблица 3

Таблица данных

Значение х	40	60	75	85	101	36	56
Буква	С	Р	И	Н	Г	Е	Й

Заполните табл. 4 и 5, учитывая полученные результаты и соответствующие буквы, и Вы узнаете имя замечательного русского поэта.

Таблица 4

Имя русского поэта

Значение х	40	36	60	101	36	56
Соответствующая буква	?	?	?	?	?	?

Фамилия русского поэта

Таблица 5

Значение х	36	40	36	85	75	85
Соответствующая буква	?	?	?	?	?	?

Задание 5. Тема: «Деление на однозначное число».

Бобр отличный пловец и ныряльщик. Узнай, какое максимальное время он может находиться под водой, выбрав наименьшее из по лученных значений ‘х’ (см. рис. 5), используя табл. 6.

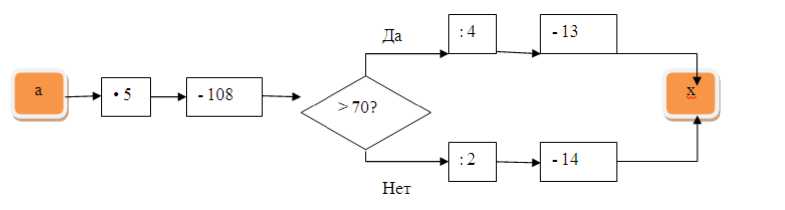
Рис 5. Алгоритм

Таблица 6

Таблица данных

Число a	32	36	44
Результат х	?	?	?

С алгоритмами ученики встречаются не только в образовательном процессе, но и в повседневной жизни ежечасно и ежедневно приходится сталкиваться с определенными правилами, указывающими на последовательность некоторых действий, поэтому на уроках были рассмотрены алгоритмы, связанные с жизненными ситуациями. Рассматривая подобные алгоритмы, ученики выстраивали логическую цепочку рассуждений, что особенно важно при изучении математики.

Последний вид алгоритмов, предложенный учащимся, – это циклические алгоритмы. Данный вид алгоритмов сначала вызывал затруднения у учащихся. Так, выстраивать логическую цепочку рассуждений сначала помогал учитель, задавая определенные вопросы: «О чем говорится в данном алгоритме?», «Что означают стрелки?», «Как вы думаете, почему стрелка возвращается на начало?».

Задание 6. Тема: «Работа с данными». Во время большой перемены проголодавшийся школьник зашёл в столовую с намерением поесть пирожков. Прокомментируйте его действия (см. рис. 6 на с. 12).

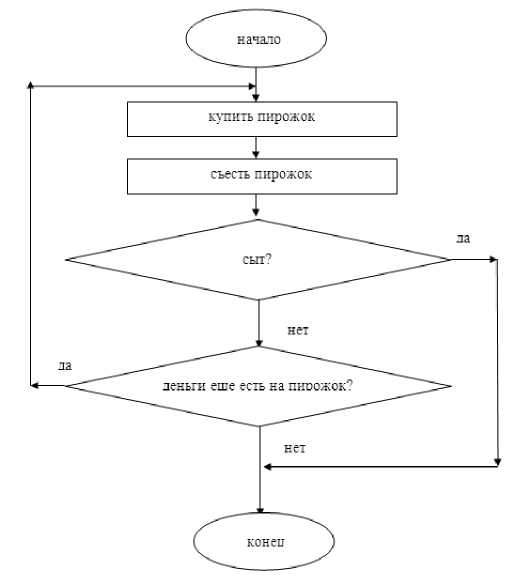
Рис. 6. Алгоритм

Включая в процессе обучения математике перечисленные задания, нами была проведена повторная диагностика сформированности универсальных учебных действий.

Получены следующие результаты: высокий уровень – 14 чел., средний – 5 чел., низкий – 2 чел.

Таким образом, исходя из данных, полученных в ходе проведенного нами исследования, можно сделать вывод о том, что одним из средств формирования регулятивных учебных действий является алгоритм.